人教版数学七年级上册3.4实际问题与一元一次方程 课件(共17张ppt)
文档属性
| 名称 | 人教版数学七年级上册3.4实际问题与一元一次方程 课件(共17张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 997.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览






文档简介
3.4实际问题与一元一次方程
1.会根据实际问题中数量关系列方程解决问题,
熟练掌握一元一次方程的解法。
2 .经历分析实际问题中的数量关系,运用方程解
决实际问题的过程,培养数学建模能力以及分析
问题、解决问题的能力。
2(3-x)=4x
去括号,得
6-2x=4x
移项,得
-2x- 4x=-6
合并同类项,得
-6x= -6
系数化成1,得
x=1
动手做一做
?
解方程 (1)
解:
2x+4(x+2)=20
去括号,得 2x+4x+8=20
合并同类项,得 6x=12
系数化为1,得 x=2
移项,得 6x=20-8
动手做一做
?
解方程 (2)
去分母(两边同时乘以5),得
解:
例1 某车间有22名工人,每人每天可以生产 1 200个螺钉或2 000个螺母. 1个螺钉需要配 2个螺 母,为使每天生产的螺钉和螺母刚好配套,应安 排生产螺钉和螺母的工人各多少名?
分析:为使每天生产的螺钉和螺母刚好配套,螺母的数量应该是螺钉数量的2倍。
找出题中所有等量关系?
1、生产螺钉人数+生产螺母的人数=22
2、2 ×螺钉=螺母。
问题探究
?
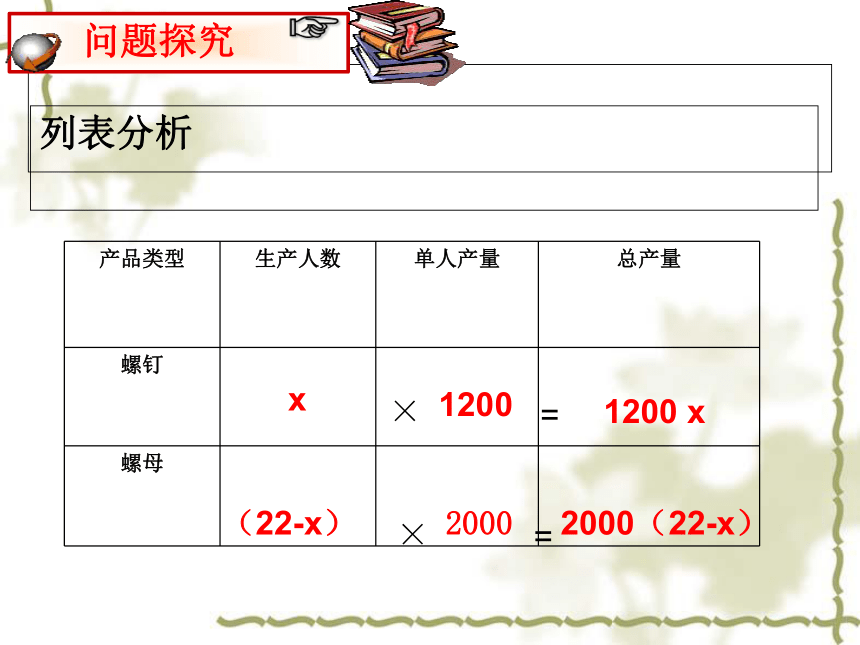
列表分析
产品类型
生产人数
单人产量
总产量
螺钉
螺母
x
1200
1200 x
(22-x)
2000
2000(22-x)
×
×
=
=
问题探究
?
例1、某车间有22名工人,每人每天可以生产1200个
螺钉或2000个螺母。1个螺钉需要配2个螺母,为使
每天生产的螺钉和螺母刚好配套,应安排生产螺钉和
螺母的工人各多少名?
解:
设应安排x名工人生产螺钉,(22-x)名工人生产螺母
2000(22-x)=2×1200x
5(22-x)=6x
110-5x=6x
11x=110
X=10
22-x=12
答:应安排10名工人生产螺钉,12名工人生产螺母。
工作量=工作效率×工作时间
工作效率=
工作量常常作为单位“1”
工程问题
复习回顾
?
1、一件工作若甲单独做20小时完成,①那么甲
单独每小时完成全部工作量的 ,即甲的
工作效率是 。
②若甲工作了3小时,完成的工作量
是 ,
③若甲单独工作 x 小时,完成的工作量
是 。
做一做
?
例2 整理一批图书,由一个人做要40 小时完成,现在计划由一部分人先做4 小时,再增加两人和他们一起做8小时,完成这项工作,假设这些人的工件效率相同,具体先安排多少人工作?
分析:①这道题已知什么?求什么?最终的 相等关 系是什么?
各阶段的工作量的和=总工作量
②工作量如何计算 ?
工作量=人均效率×人数×时间
③在列方程时,可以把全部工作量看作什么?
1
问题探究
?
?工作人数
工作效率
工作时间
工作量
总工作量
先X人
再增加2人(x+2)人
8
4
1
问题探究
?
列表分析
工作量=人均效率×人数×时间
问题1 整理一批图书,由一个人做要40 小时完成,现在计划由一部分人先做4 小时,再增加两人和他们一起做8小时,完成这项工作,假设这些人的工件效率相同,具体先安排多少人工作?
解:设先安排 x名工人工作4小时,由题意,得
去分母,得 4x+8(x+2)=40
去括号,得 4x+8x+16=40
移项及合并,得 12x=24
系数化为1,得 x=2
答:应先安排 2名工人工作4小时
问题探究
?
1、一套仪器由一个A部件和三个B部件构成。用1立方米
钢材可做40个A部件或240个B部件。现要用6立方米钢材
制作这种仪器,应用多少钢材做A部件,多少钢材做B部件,
恰好配成这种仪器多少套?
分析:
根据题意知B部件的数量是A部件数量的3倍这一等量关系
式得方程。
解:设应用x立方米钢材做A部件,则应用(6-x)立方米做B部
件,根据 题意得方程:
(40x)×3=(6-x) ×240
解方程,得
X=(6-x) ×2
3x=12
X=4
6-x=2
答:
应用4立方米钢材做A部件,应用2立方米钢材做B部件
练习
练习
2、一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天。如果由这两个工程队从两端同时施工,要多少天可以铺好这条管线?
分析:
把工作量看作单位“1‘”,则甲的工作效率为:
1
12
乙的工作效率为:
1
24
根据工作效率×工作时间=工作量,得方程。
解:设要x天可以铺好这条管线,由题意得,
1
12
x
+
1
24
x
=1
解方程,得
2x+x=24
3x=24
X=8
答:要8天可以铺好这条管线。
归纳小结:
用一元一次方程解决实际问题的基本过程如下:
实际问题
设未知数,列方程
一元一次方程
实际问题的答案
解方程
一元一次方程的解
(x=a)
检验
这一过程包括设、列、解、检、答等步骤,即设未知数,
列方程,解方程,检验所得结果,确定答案。正确分析问
题中的相等关系是列方程的基础。
布置作业
?
必做题1、
选做题2、
祝同学们学习进步! 再见
1.会根据实际问题中数量关系列方程解决问题,
熟练掌握一元一次方程的解法。
2 .经历分析实际问题中的数量关系,运用方程解
决实际问题的过程,培养数学建模能力以及分析
问题、解决问题的能力。
2(3-x)=4x
去括号,得
6-2x=4x
移项,得
-2x- 4x=-6
合并同类项,得
-6x= -6
系数化成1,得
x=1
动手做一做
?
解方程 (1)
解:
2x+4(x+2)=20
去括号,得 2x+4x+8=20
合并同类项,得 6x=12
系数化为1,得 x=2
移项,得 6x=20-8
动手做一做
?
解方程 (2)
去分母(两边同时乘以5),得
解:
例1 某车间有22名工人,每人每天可以生产 1 200个螺钉或2 000个螺母. 1个螺钉需要配 2个螺 母,为使每天生产的螺钉和螺母刚好配套,应安 排生产螺钉和螺母的工人各多少名?
分析:为使每天生产的螺钉和螺母刚好配套,螺母的数量应该是螺钉数量的2倍。
找出题中所有等量关系?
1、生产螺钉人数+生产螺母的人数=22
2、2 ×螺钉=螺母。
问题探究
?
列表分析
产品类型
生产人数
单人产量
总产量
螺钉
螺母
x
1200
1200 x
(22-x)
2000
2000(22-x)
×
×
=
=
问题探究
?
例1、某车间有22名工人,每人每天可以生产1200个
螺钉或2000个螺母。1个螺钉需要配2个螺母,为使
每天生产的螺钉和螺母刚好配套,应安排生产螺钉和
螺母的工人各多少名?
解:
设应安排x名工人生产螺钉,(22-x)名工人生产螺母
2000(22-x)=2×1200x
5(22-x)=6x
110-5x=6x
11x=110
X=10
22-x=12
答:应安排10名工人生产螺钉,12名工人生产螺母。
工作量=工作效率×工作时间
工作效率=
工作量常常作为单位“1”
工程问题
复习回顾
?
1、一件工作若甲单独做20小时完成,①那么甲
单独每小时完成全部工作量的 ,即甲的
工作效率是 。
②若甲工作了3小时,完成的工作量
是 ,
③若甲单独工作 x 小时,完成的工作量
是 。
做一做
?
例2 整理一批图书,由一个人做要40 小时完成,现在计划由一部分人先做4 小时,再增加两人和他们一起做8小时,完成这项工作,假设这些人的工件效率相同,具体先安排多少人工作?
分析:①这道题已知什么?求什么?最终的 相等关 系是什么?
各阶段的工作量的和=总工作量
②工作量如何计算 ?
工作量=人均效率×人数×时间
③在列方程时,可以把全部工作量看作什么?
1
问题探究
?
?工作人数
工作效率
工作时间
工作量
总工作量
先X人
再增加2人(x+2)人
8
4
1
问题探究
?
列表分析
工作量=人均效率×人数×时间
问题1 整理一批图书,由一个人做要40 小时完成,现在计划由一部分人先做4 小时,再增加两人和他们一起做8小时,完成这项工作,假设这些人的工件效率相同,具体先安排多少人工作?
解:设先安排 x名工人工作4小时,由题意,得
去分母,得 4x+8(x+2)=40
去括号,得 4x+8x+16=40
移项及合并,得 12x=24
系数化为1,得 x=2
答:应先安排 2名工人工作4小时
问题探究
?
1、一套仪器由一个A部件和三个B部件构成。用1立方米
钢材可做40个A部件或240个B部件。现要用6立方米钢材
制作这种仪器,应用多少钢材做A部件,多少钢材做B部件,
恰好配成这种仪器多少套?
分析:
根据题意知B部件的数量是A部件数量的3倍这一等量关系
式得方程。
解:设应用x立方米钢材做A部件,则应用(6-x)立方米做B部
件,根据 题意得方程:
(40x)×3=(6-x) ×240
解方程,得
X=(6-x) ×2
3x=12
X=4
6-x=2
答:
应用4立方米钢材做A部件,应用2立方米钢材做B部件
练习
练习
2、一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天。如果由这两个工程队从两端同时施工,要多少天可以铺好这条管线?
分析:
把工作量看作单位“1‘”,则甲的工作效率为:
1
12
乙的工作效率为:
1
24
根据工作效率×工作时间=工作量,得方程。
解:设要x天可以铺好这条管线,由题意得,
1
12
x
+
1
24
x
=1
解方程,得
2x+x=24
3x=24
X=8
答:要8天可以铺好这条管线。
归纳小结:
用一元一次方程解决实际问题的基本过程如下:
实际问题
设未知数,列方程
一元一次方程
实际问题的答案
解方程
一元一次方程的解
(x=a)
检验
这一过程包括设、列、解、检、答等步骤,即设未知数,
列方程,解方程,检验所得结果,确定答案。正确分析问
题中的相等关系是列方程的基础。
布置作业
?
必做题1、
选做题2、
祝同学们学习进步! 再见
