人教版数学七年级上册4.2.2比较线段的长短 课件(共16张ppt)
文档属性
| 名称 | 人教版数学七年级上册4.2.2比较线段的长短 课件(共16张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 155.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 15:27:03 | ||
图片预览


文档简介
第二节 比较线段的长短
人教版七年级数学上册
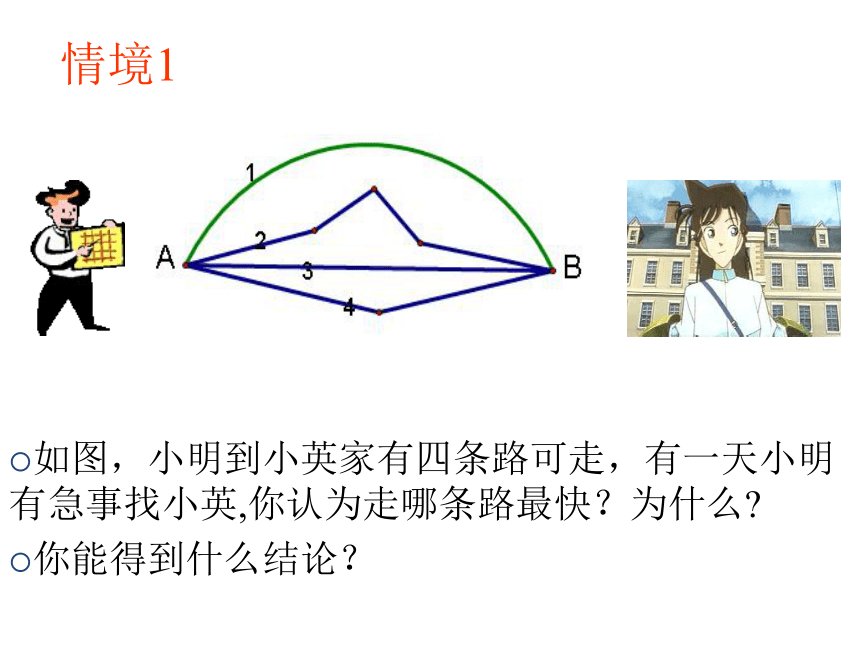
如图,小明到小英家有四条路可走,有一天小明有急事找小英,你认为走哪条路最快?为什么?
你能得到什么结论?
情境1
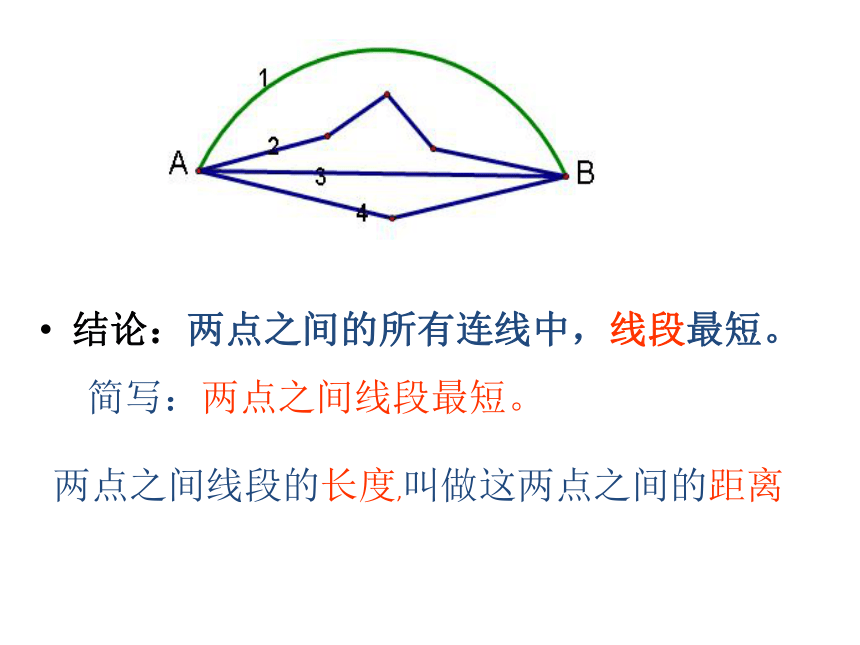
结论:两点之间的所有连线中,线段最短。
简写:两点之间线段最短。
两点之间线段的长度,叫做这两点之间的距离
A
比较线段长短的两种方法:
1、度量法——从“数值”的角度比较
工具:刻度尺
2、叠合法——从“形”的角度比较
工具:圆规
(起点对齐,看终点)
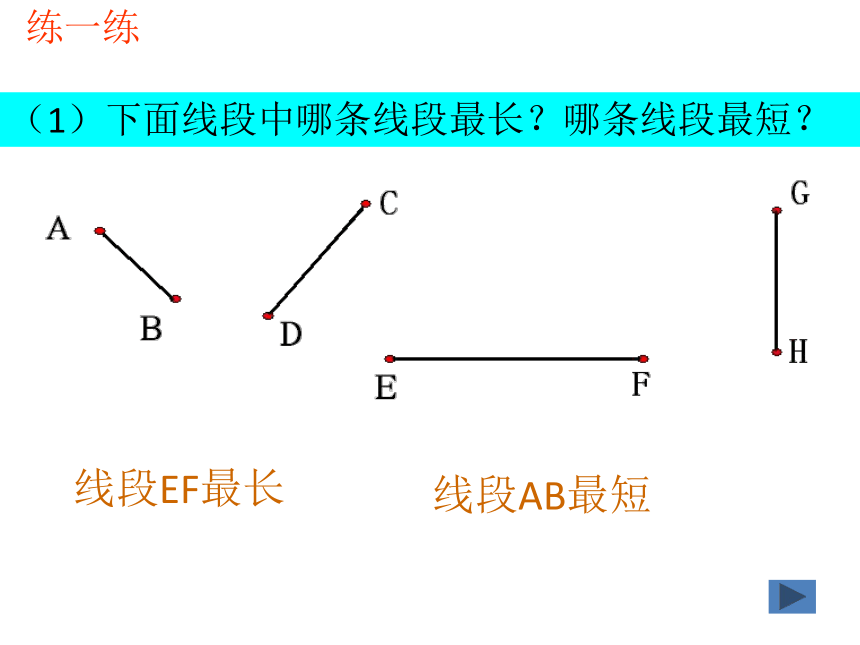
线段EF最长
线段AB最短
练一练
(1)下面线段中哪条线段最长?哪条线段最短?
(1)
a
b
(3)
(2)
a
b
a
b
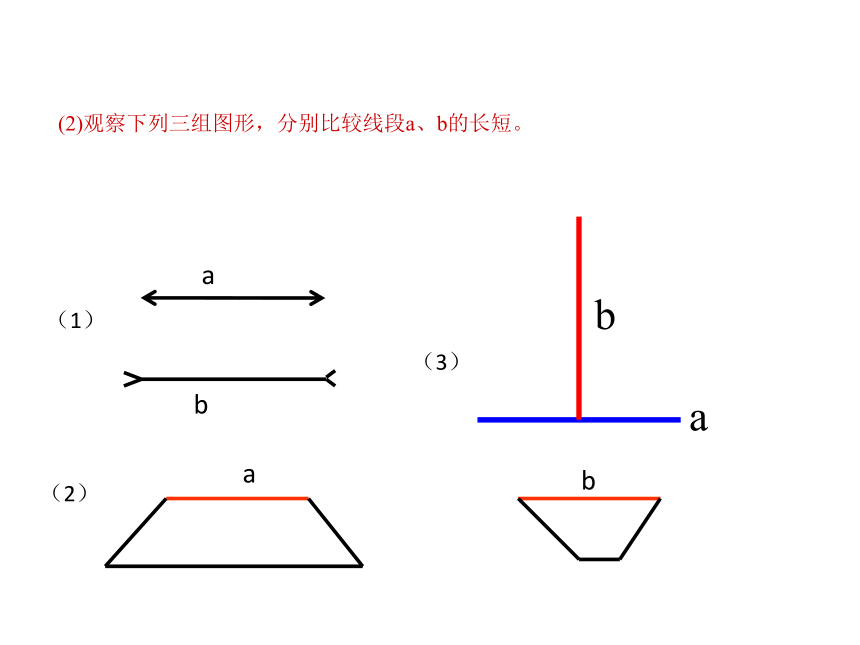
(2)观察下列三组图形,分别比较线段a、b的长短。
A
B
C
点C把线段AB分成相等的两条线段AC与BC,点C叫做线段AB的中点(midpoint),
问题
如图,若点C为线段AB的中点,用几何符号如何表示?
(2)AC=CB= AB
(1)AC=CB
(3)AB=2AC=2CB
我们将一根绳子对折,可以得到一个点,这个点将这条绳子分成了两根相等的绳子。如果我们把这条绳子看作一条线段,这个点就把这条线段分成了两条相等的线段。这个点就是这条线段的中点。
1. 如图,AB=6cm,点C是线段AB的中点,点D是线段CB的中点,则 AC=___ CD=______
A
D
C
B
中点应用
2.判断:若AM=BM,则M为线段AB的中点。
A
B
M
线段中点的条件:
1、在已知线段上。
2、把已知线段分成两条相等线段的点.
3cm
1.5cm
二、学习了怎样比较线段的长短。
1、度量法:从“数值”的角度比较。
2、叠合法:从“形”的角度比较。(起点对齐,看终点)
本节课你又增长了哪些知识?
谈谈收获吧
三、尺规作图
用尺规法画一条线段等于已知线段。
概括为:(1)画(2)量(3)截
四、知道线段中点的定义,会用几何符号表示线段的中点。
一、结论:两点之间线段最短。
两点之间线段的长度,叫做这两点之间的距离
达标测试
1、将弯曲的河道改直,可以缩短航程,是因为
两点之间,线段最短。
2、关于两点之间的距离,下列说法不正确的是( )
A、连接两点的线段的长度,是两点之间的距离。
B、如果AB=AC,那么点A到点B的距离等于点A到点
C的距离。
C、连接两点的线段就是两点之间的距离.
D、两点之间的距离是连接这两点的所有的线的长度中,长度最短的。
C
例题解析
3、在直线l上顺次截取A,B,C三点,使得 AB=4cm,BC=3cm。如果O是线段AC的中点, 线段AO的长是( )cm。
B
l
A
C
O
3.5
例题解析
4、怎样比较AM与BM的长短?
A
B
C
D
M
如图,A,B是河流n两旁的两个村庄,现要在河边建一个引水站向两村供水,问引水站建在什么地方才能使所需的管道最短?
请在图中标出引水站的位置P,并说明你的理由。
拓展延伸1
如图是一个四边形,在各边上任意取一点,并顺次连接它们,想一想你得到的图形周长与原四边形周长哪一个大?为什么?如果是一个五边形呢?六边形呢?
拓展延伸2
A
B
C
D
E
F
G
H
公元前五世纪的希腊数学家,已经习惯于用不带刻度的直尺和圆规(以下简称尺规)来作图了。在他们看来,直线和圆是可以信赖的最基本的图形,而直尺和圆规是这两种图形的具体体现,因而只有用尺规作出的图形才是可信的。于是他们热衷于在尺规限制下探讨几何作图问题。数学家们总是对用简单的工具解决困难的问题备加赞赏,自然对用尺规去画各种图形饶有兴趣。尺规作图是对人类智慧的挑战,是培养人的思维与操作能力的有效手段。
数学小趣闻—尺规作图
谢 谢
人教版七年级数学上册
如图,小明到小英家有四条路可走,有一天小明有急事找小英,你认为走哪条路最快?为什么?
你能得到什么结论?
情境1
结论:两点之间的所有连线中,线段最短。
简写:两点之间线段最短。
两点之间线段的长度,叫做这两点之间的距离
A
比较线段长短的两种方法:
1、度量法——从“数值”的角度比较
工具:刻度尺
2、叠合法——从“形”的角度比较
工具:圆规
(起点对齐,看终点)
线段EF最长
线段AB最短
练一练
(1)下面线段中哪条线段最长?哪条线段最短?
(1)
a
b
(3)
(2)
a
b
a
b
(2)观察下列三组图形,分别比较线段a、b的长短。
A
B
C
点C把线段AB分成相等的两条线段AC与BC,点C叫做线段AB的中点(midpoint),
问题
如图,若点C为线段AB的中点,用几何符号如何表示?
(2)AC=CB= AB
(1)AC=CB
(3)AB=2AC=2CB
我们将一根绳子对折,可以得到一个点,这个点将这条绳子分成了两根相等的绳子。如果我们把这条绳子看作一条线段,这个点就把这条线段分成了两条相等的线段。这个点就是这条线段的中点。
1. 如图,AB=6cm,点C是线段AB的中点,点D是线段CB的中点,则 AC=___ CD=______
A
D
C
B
中点应用
2.判断:若AM=BM,则M为线段AB的中点。
A
B
M
线段中点的条件:
1、在已知线段上。
2、把已知线段分成两条相等线段的点.
3cm
1.5cm
二、学习了怎样比较线段的长短。
1、度量法:从“数值”的角度比较。
2、叠合法:从“形”的角度比较。(起点对齐,看终点)
本节课你又增长了哪些知识?
谈谈收获吧
三、尺规作图
用尺规法画一条线段等于已知线段。
概括为:(1)画(2)量(3)截
四、知道线段中点的定义,会用几何符号表示线段的中点。
一、结论:两点之间线段最短。
两点之间线段的长度,叫做这两点之间的距离
达标测试
1、将弯曲的河道改直,可以缩短航程,是因为
两点之间,线段最短。
2、关于两点之间的距离,下列说法不正确的是( )
A、连接两点的线段的长度,是两点之间的距离。
B、如果AB=AC,那么点A到点B的距离等于点A到点
C的距离。
C、连接两点的线段就是两点之间的距离.
D、两点之间的距离是连接这两点的所有的线的长度中,长度最短的。
C
例题解析
3、在直线l上顺次截取A,B,C三点,使得 AB=4cm,BC=3cm。如果O是线段AC的中点, 线段AO的长是( )cm。
B
l
A
C
O
3.5
例题解析
4、怎样比较AM与BM的长短?
A
B
C
D
M
如图,A,B是河流n两旁的两个村庄,现要在河边建一个引水站向两村供水,问引水站建在什么地方才能使所需的管道最短?
请在图中标出引水站的位置P,并说明你的理由。
拓展延伸1
如图是一个四边形,在各边上任意取一点,并顺次连接它们,想一想你得到的图形周长与原四边形周长哪一个大?为什么?如果是一个五边形呢?六边形呢?
拓展延伸2
A
B
C
D
E
F
G
H
公元前五世纪的希腊数学家,已经习惯于用不带刻度的直尺和圆规(以下简称尺规)来作图了。在他们看来,直线和圆是可以信赖的最基本的图形,而直尺和圆规是这两种图形的具体体现,因而只有用尺规作出的图形才是可信的。于是他们热衷于在尺规限制下探讨几何作图问题。数学家们总是对用简单的工具解决困难的问题备加赞赏,自然对用尺规去画各种图形饶有兴趣。尺规作图是对人类智慧的挑战,是培养人的思维与操作能力的有效手段。
数学小趣闻—尺规作图
谢 谢
