人教版数学七年级上册4.3.1角 课件(共18张ppt)
文档属性
| 名称 | 人教版数学七年级上册4.3.1角 课件(共18张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 12:26:02 | ||
图片预览



文档简介
创设情境 引入新课
你是如何画角的?
你能描述一下怎样的几何图形叫做角吗?
层层深入 探索新知
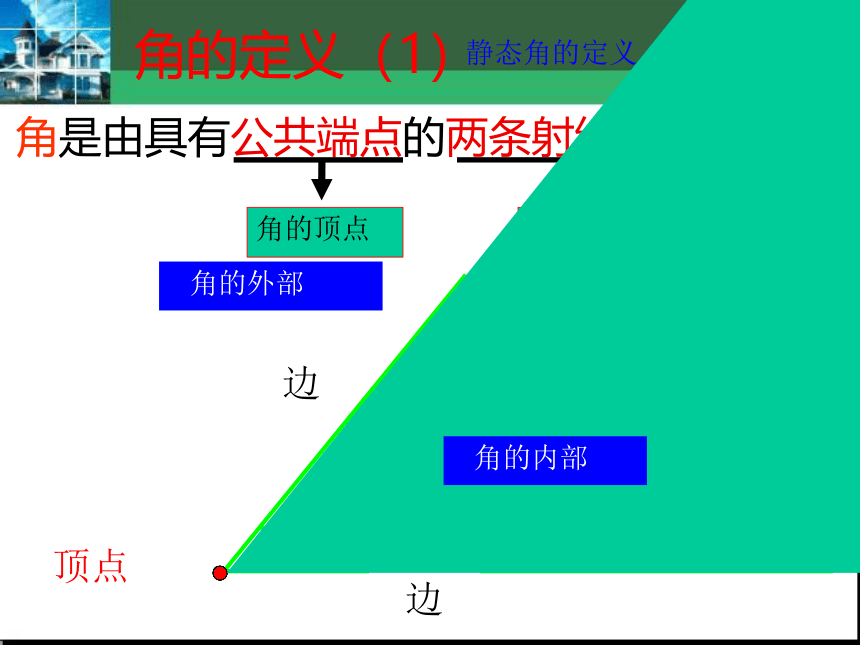
角是由具有公共端点的两条射线组成的图形.
顶点
射线
射线
边
边
角的定义(1)
静态角的定义
角的顶点
角的边
角的内部
角的外部
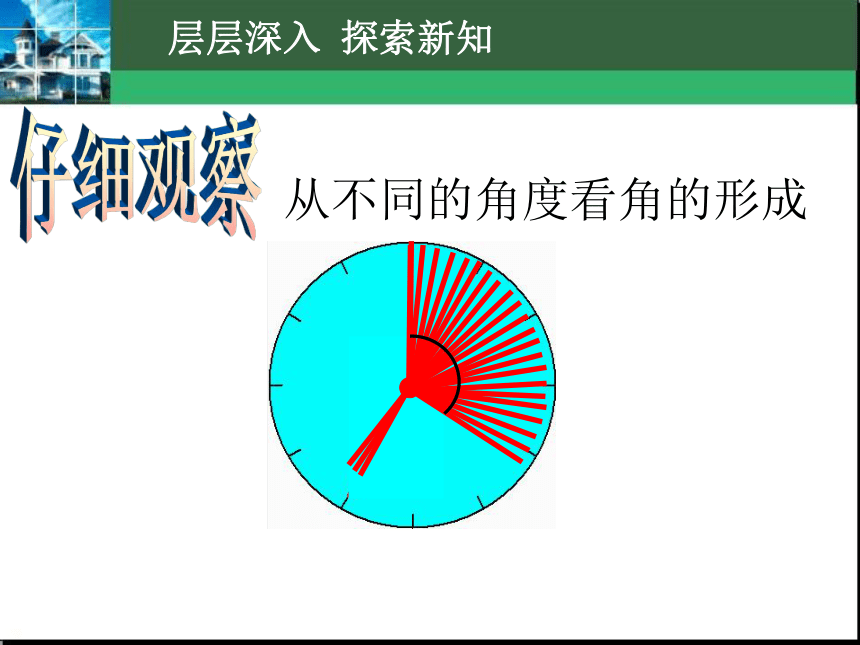
从不同的角度看角的形成
层层深入 探索新知
角的定义(2):
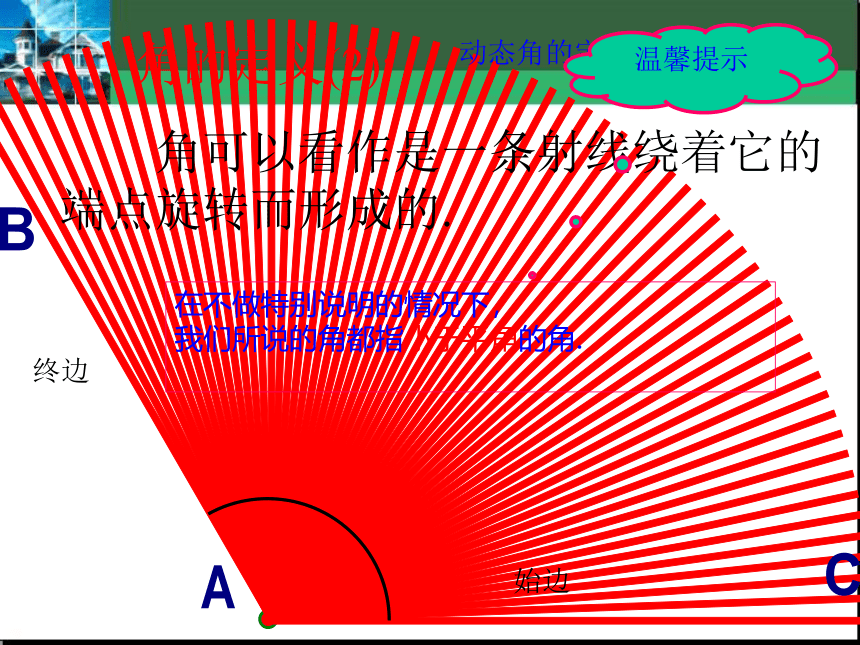
动态角的定义
角可以看作是一条射线绕着它的端点旋转而形成的.
温馨提示
在不做特别说明的情况下,
我们所说的角都指小于平角的角.
始边
终边
O
A
一条射线绕端点旋转,得到了( )
A 锐角 B 直角 C 钝角 D 平角 E 周角
B
B
B
B
(B)
B
B
层层深入 探索新知
强化概念 学以致用
角用符号“ ”表示,读做“角”.
(1)用三个大写字母表示,但表示顶点的字母一定要写在中间.
如∠AOB或∠BOA
(2) 用一个字母表示角,
如∠O
∠
A
O
B
∠
(3) 用一个数字表示角,在靠近顶点处画上弧线,写上数字.
如∠1
1
(4)用一个希腊字母表示,在靠近顶点处画上弧线,写上希腊字母.
如∠α
α
但必须是以这个字母为顶点的角只有一个.
C
P
O
C
A
①⑥
1.将图中的角表示成下列形式:
①∠APO ②∠AOP ③ OPC
④∠O ⑤∠COP ⑥∠P
其中正确的有
(把你认为正确的序号都填上.)
强化概念 学以致用
2.如图,回答下列问题:
C
D
B
A
(1)∠ABD与∠ABC是同一个角吗?
(2)能用一个大写字母表示的角有几个?
(3)以点A为顶点的角有哪几个?以点D为顶点的角呢?
(4)图中共有多少个角?分别是哪些角?
(4)解:7个,分别是
∠ABC、 ∠ACB
∠BAC、 ∠BAD、 ∠CAD
∠ADB、 ∠ADC
(3)解:
强化概念 学以致用
创设情境 引入新课
1°
把一个周角360等分,每一份就是1度的角,记做1°.除了“度”之外,还有其它的度量单位吗?
1°的60分之一为1分,记作1′,即1°=60′
1′的60分之一为1秒,记作1″,即1′=60″
角的度、分、秒是60进制的,这和计量时间的时、分、秒是一样的.
例1
计算:
⑴1.45°等于多少分? 等于多少秒?
⑵1800″等于多少分? 等于多少度?
解: ⑴1.45 ×60′
=87′,
即 1.45°=87′=5220″.
⑵
=30′
87×60″
=5220″,
强化概念 学以致用
′
°
=0.5
°
讨论
3 ° 15′ 与3 . 15°相等吗?
解:3 ° 15′=3.25° 3.25° 大于3 . 15° (转化为度)
3.15°=3°9′ 3°9′ 小于3 ° 15′(转化为度、分)
3 ° 15′=195′ 3 . 15°=189′ (转化为分)
195′ 大于189′ 所以3 ° 15′ 大于3 . 15°
角
有公共端点的两条射线
组成的图形
一条射线绕着它的端点
旋转而成的图形
用三个大写字母或
一个大写字表示.
用一个数字表示
用一个希腊字母表示
角的定义
角的表示方法
角的度量
度、分、秒
课堂小结 感悟收获
若∠AOB内没有射线,则图中一共有 个角。
若∠AOB内有1条射线,则图中一共有 个角。
若∠AOB内有2条射线,则图中一共有 个角。
若∠AOB内有10条射线,则图中一共有 个角。
……
1
3
6
66
A
B
O
A1
A2
你是如何画角的?
你能描述一下怎样的几何图形叫做角吗?
层层深入 探索新知
角是由具有公共端点的两条射线组成的图形.
顶点
射线
射线
边
边
角的定义(1)
静态角的定义
角的顶点
角的边
角的内部
角的外部
从不同的角度看角的形成
层层深入 探索新知
角的定义(2):
动态角的定义
角可以看作是一条射线绕着它的端点旋转而形成的.
温馨提示
在不做特别说明的情况下,
我们所说的角都指小于平角的角.
始边
终边
O
A
一条射线绕端点旋转,得到了( )
A 锐角 B 直角 C 钝角 D 平角 E 周角
B
B
B
B
(B)
B
B
层层深入 探索新知
强化概念 学以致用
角用符号“ ”表示,读做“角”.
(1)用三个大写字母表示,但表示顶点的字母一定要写在中间.
如∠AOB或∠BOA
(2) 用一个字母表示角,
如∠O
∠
A
O
B
∠
(3) 用一个数字表示角,在靠近顶点处画上弧线,写上数字.
如∠1
1
(4)用一个希腊字母表示,在靠近顶点处画上弧线,写上希腊字母.
如∠α
α
但必须是以这个字母为顶点的角只有一个.
C
P
O
C
A
①⑥
1.将图中的角表示成下列形式:
①∠APO ②∠AOP ③ OPC
④∠O ⑤∠COP ⑥∠P
其中正确的有
(把你认为正确的序号都填上.)
强化概念 学以致用
2.如图,回答下列问题:
C
D
B
A
(1)∠ABD与∠ABC是同一个角吗?
(2)能用一个大写字母表示的角有几个?
(3)以点A为顶点的角有哪几个?以点D为顶点的角呢?
(4)图中共有多少个角?分别是哪些角?
(4)解:7个,分别是
∠ABC、 ∠ACB
∠BAC、 ∠BAD、 ∠CAD
∠ADB、 ∠ADC
(3)解:
强化概念 学以致用
创设情境 引入新课
1°
把一个周角360等分,每一份就是1度的角,记做1°.除了“度”之外,还有其它的度量单位吗?
1°的60分之一为1分,记作1′,即1°=60′
1′的60分之一为1秒,记作1″,即1′=60″
角的度、分、秒是60进制的,这和计量时间的时、分、秒是一样的.
例1
计算:
⑴1.45°等于多少分? 等于多少秒?
⑵1800″等于多少分? 等于多少度?
解: ⑴1.45 ×60′
=87′,
即 1.45°=87′=5220″.
⑵
=30′
87×60″
=5220″,
强化概念 学以致用
′
°
=0.5
°
讨论
3 ° 15′ 与3 . 15°相等吗?
解:3 ° 15′=3.25° 3.25° 大于3 . 15° (转化为度)
3.15°=3°9′ 3°9′ 小于3 ° 15′(转化为度、分)
3 ° 15′=195′ 3 . 15°=189′ (转化为分)
195′ 大于189′ 所以3 ° 15′ 大于3 . 15°
角
有公共端点的两条射线
组成的图形
一条射线绕着它的端点
旋转而成的图形
用三个大写字母或
一个大写字表示.
用一个数字表示
用一个希腊字母表示
角的定义
角的表示方法
角的度量
度、分、秒
课堂小结 感悟收获
若∠AOB内没有射线,则图中一共有 个角。
若∠AOB内有1条射线,则图中一共有 个角。
若∠AOB内有2条射线,则图中一共有 个角。
若∠AOB内有10条射线,则图中一共有 个角。
……
1
3
6
66
A
B
O
A1
A2
