人教版八年级数学上学期《12.2 三角形全等的判定》 同步练习(Word版 含解析)
文档属性
| 名称 | 人教版八年级数学上学期《12.2 三角形全等的判定》 同步练习(Word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 124.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览


文档简介
12.2
三角形全等的判定
一.选择题
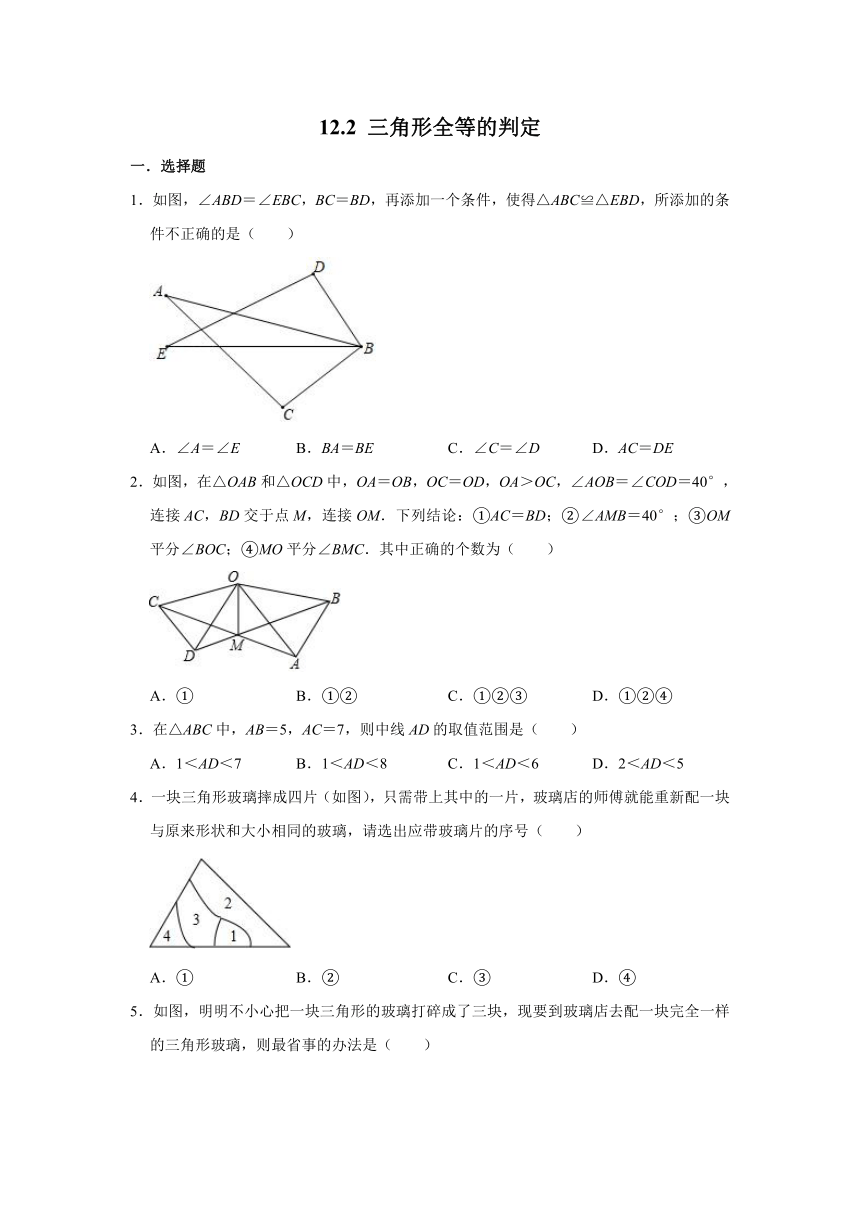
1.如图,∠ABD=∠EBC,BC=BD,再添加一个条件,使得△ABC≌△EBD,所添加的条件不正确的是( )
A.∠A=∠E
B.BA=BE
C.∠C=∠D
D.AC=DE
2.如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的个数为( )
A.①
B.①②
C.①②③
D.①②④
3.在△ABC中,AB=5,AC=7,则中线AD的取值范围是( )
A.1<AD<7
B.1<AD<8
C.1<AD<6
D.2<AD<5
4.一块三角形玻璃摔成四片(如图),只需带上其中的一片,玻璃店的师傅就能重新配一块与原来形状和大小相同的玻璃,请选出应带玻璃片的序号( )
A.①
B.②
C.③
D.④
5.如图,明明不小心把一块三角形的玻璃打碎成了三块,现要到玻璃店去配一块完全一样的三角形玻璃,则最省事的办法是( )
A.带(1)去
B.带(2)去
C.带(3)去
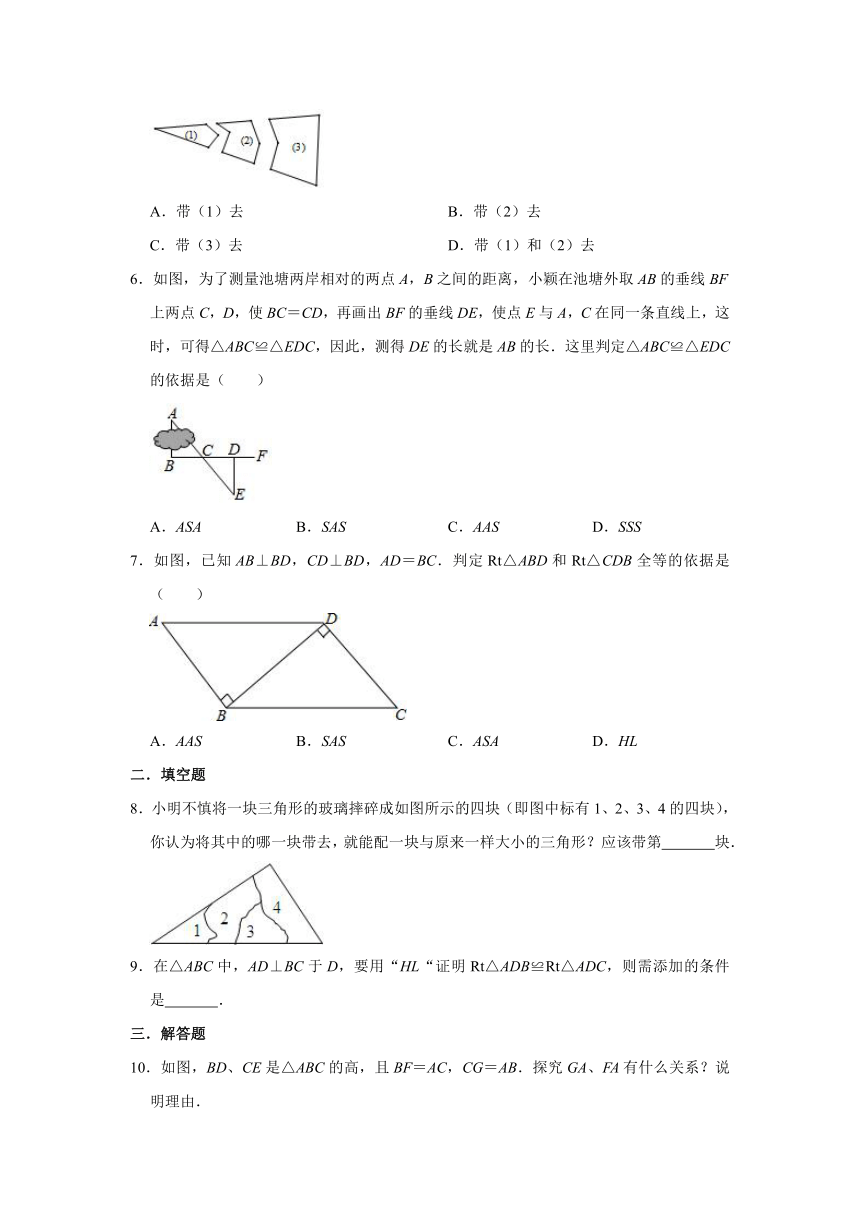
D.带(1)和(2)去
6.如图,为了测量池塘两岸相对的两点A,B之间的距离,小颖在池塘外取AB的垂线BF上两点C,D,使BC=CD,再画出BF的垂线DE,使点E与A,C在同一条直线上,这时,可得△ABC≌△EDC,因此,测得DE的长就是AB的长.这里判定△ABC≌△EDC的依据是( )
A.ASA
B.SAS
C.AAS
D.SSS
7.如图,已知AB⊥BD,CD⊥BD,AD=BC.判定Rt△ABD和Rt△CDB全等的依据是( )
A.AAS
B.SAS
C.ASA
D.HL
二.填空题
8.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带第
块.
9.在△ABC中,AD⊥BC于D,要用“HL“证明Rt△ADB≌Rt△ADC,则需添加的条件是
.
三.解答题
10.如图,BD、CE是△ABC的高,且BF=AC,CG=AB.探究GA、FA有什么关系?说明理由.
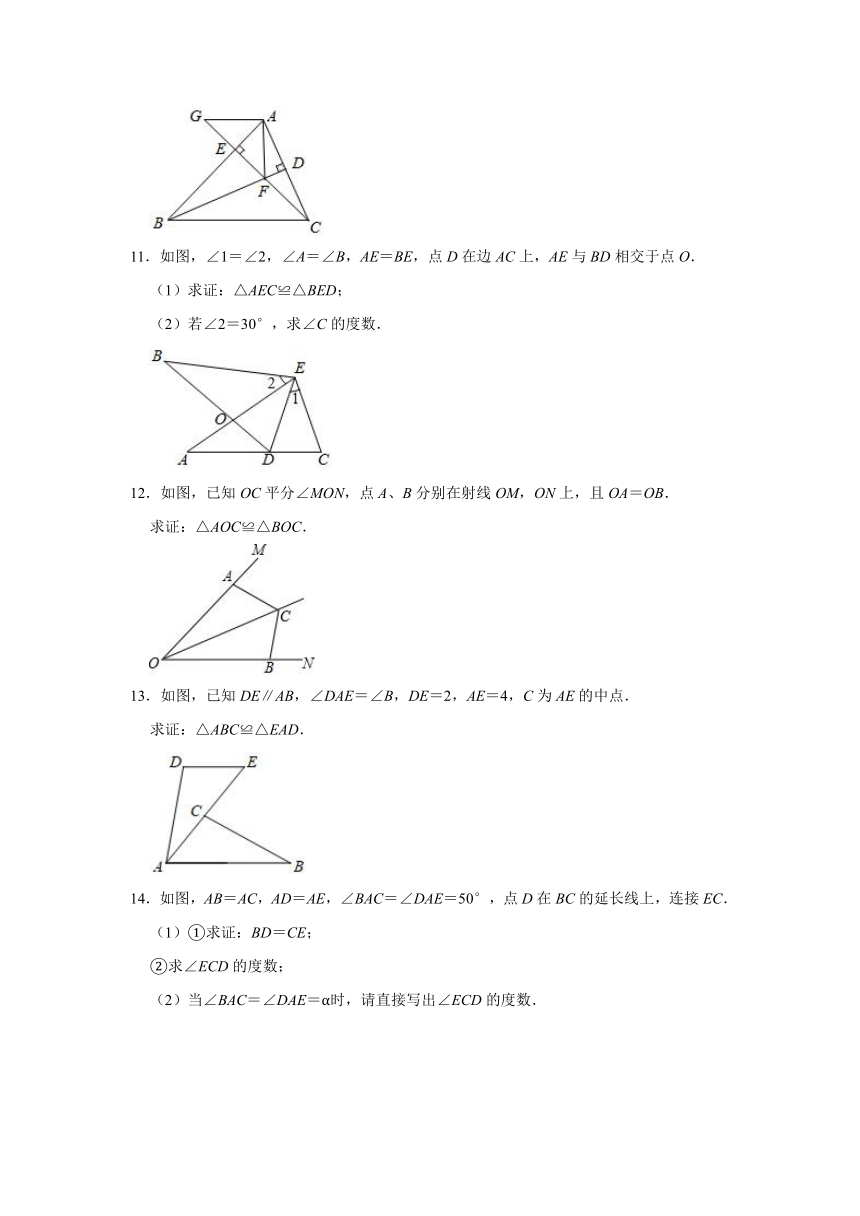
11.如图,∠1=∠2,∠A=∠B,AE=BE,点D在边AC上,AE与BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠2=30°,求∠C的度数.
12.如图,已知OC平分∠MON,点A、B分别在射线OM,ON上,且OA=OB.
求证:△AOC≌△BOC.
13.如图,已知DE∥AB,∠DAE=∠B,DE=2,AE=4,C为AE的中点.
求证:△ABC≌△EAD.
14.如图,AB=AC,AD=AE,∠BAC=∠DAE=50°,点D在BC的延长线上,连接EC.
(1)①求证:BD=CE;
②求∠ECD的度数;
(2)当∠BAC=∠DAE=α时,请直接写出∠ECD的度数.
15.如图,BD为△ABC的角平分线,且BD=BC,E在BD的延长线上,连接AE,∠BAE=∠BEA,连接CE.
求证:
(1)△ABD≌△EBC;
(2)∠BCE+∠BCD=180°.
16.如图,A,D,E三点在同一直线上,∠1=∠2,∠3=∠4.
(1)求证:AB=AC;
(2)求证:AE⊥BC.
17.已知,如图,AB=AE,AB∥DE,∠D=∠ACB.
(1)求证:△ABC≌△EAD;
(2)已知:DE=3,AB=7,求CE的长.
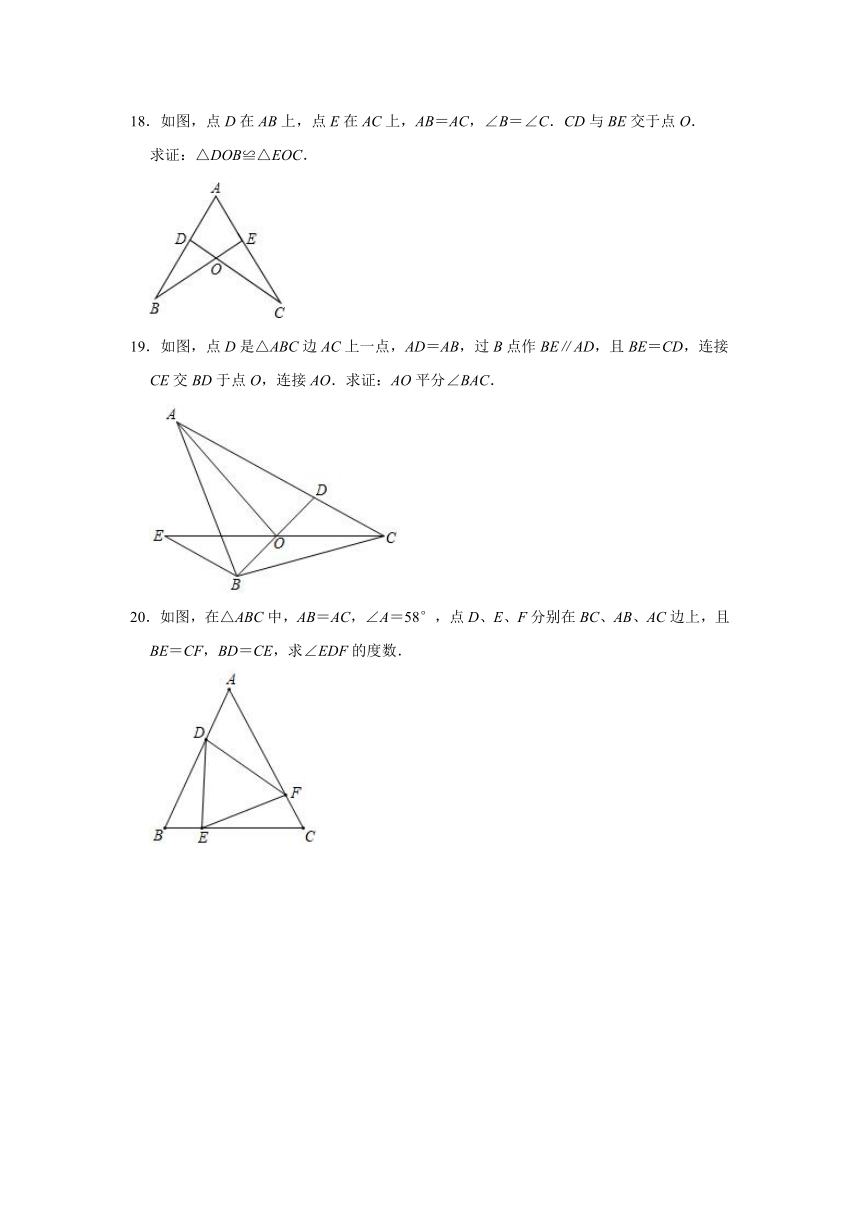
18.如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.CD与BE交于点O.
求证:△DOB≌△EOC.
19.如图,点D是△ABC边AC上一点,AD=AB,过B点作BE∥AD,且BE=CD,连接CE交BD于点O,连接AO.求证:AO平分∠BAC.
20.如图,在△ABC中,AB=AC,∠A=58°,点D、E、F分别在BC、AB、AC边上,且BE=CF,BD=CE,求∠EDF的度数.
参考答案
一.选择题
1.解:∵∠ABC=∠EBD,BC=BD,
∴当添加BA=BE时,可根据“SAS”判断△ABC≌△EBD;
当添加∠C=∠D时,可根据“ASA”判断△ABC≌△EBD;
当添加∠A=∠E时,可根据“AAS”判断△ABC≌△EBD.
故选:D.
2.解:∵∠AOB=∠COD=40°,
∴∠AOB+∠AOD=∠COD+∠AOD,
即∠AOC=∠BOD,
在△AOC和△BOD中,
,
∴△AOC≌△BOD(SAS),
∴∠OCA=∠ODB,∠OAC=∠OBD,AC=BD,①正确;
由三角形的外角性质得:∠AMB+∠OAC=∠AOB+∠OBD,
∴∠AMB=∠AOB=40°,②正确;
作OG⊥MC于G,OH⊥MB于H,如图2所示:
则∠OGC=∠OHD=90°,
在△OCG和△ODH中,
,
∴△OCG≌△ODH(AAS),
∴OG=OH,
∴MO平分∠BMC,④正确;
∵∠AOB=∠COD,
∴当∠DOM=∠AOM时,OM才平分∠BOC,
假设∠DOM=∠AOM,
∵△AOC≌△BOD,
∴∠COM=∠BOM,
∵MO平分∠BMC,
∴∠CMO=∠BMO,
在△COM和△BOM中,
,
∴△COM≌△BOM(ASA),
∴OB=OC,
∵OA=OB,
∴OA=OC,
与OA>OC矛盾,
∴③错误;
正确的有①②④;
故选:D.
3.解:延长AD到E,使AD=DE,连接BE,
∵AD是△ABC的中线,
∴BD=CD,
在△ADC与△EDB中,
,
∴△ADC≌△EDB(SAS),
∴EB=AC,
根据三角形的三边关系得:AC﹣AB<AE<AC+AB,
∴2<AE<12,
∵AE=2AD,
∴1<AD<6,
故选:C.
4.解:由图可知,带2去可以利用“角边角”得到与原三角形全等的三角形.
故选:B.
5.解:根据三角形全等的判定方法,根据角边角可确定一个全等三角形,
只有第三块玻璃包括了两角和它们的夹边,只有带(3)去才能配一块完全一样的玻璃,是符合题意的.
故选:C.
6.解:因为证明在△ABC≌△EDC用到的条件是:BC=CD,∠ABC=∠EDC=90°,∠ACB=∠ECD(对顶角相等),
所以用到的是两角及这两角的夹边对应相等即ASA这一方法.
故选:A.
7.解:∵AB⊥BD,CD⊥BD,
∴∠ABD=∠CDB=90°,
在Rt△ABD和Rt△CDB中,
,
∴Rt△ABD≌Rt△CDB(HL),
故选:D.
二.填空题
8.解:1、2、3块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,
只有第4块有完整的两角及夹边,符合ASA,满足三角形全等的条件,是符合题意的,
故答案为:4.
9.解:添加条件:AB=AC,
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△ABD和Rt△ACD中
,
∴Rt△ABD≌Rt△ACD(HL),
故答案为:AB=AC.
三.解答题
10.解:GA=FA,GA⊥FA,理由如下:
∵BD、CE是△ABC的高,
∴∠ADB=∠AEC=90°,
∴∠ABF+∠BAD=90°∠GCA+∠BAD=90°,
∴∠ABF=∠GCA,
在△ABF和△GCA中,
,
∴△ABF≌△GCA(SAS),
∴FA=GA,∠BAF=∠G,
∵CE是△ABC的高,
∴CE⊥AB,
∴∠G+∠GAE=90°,
∴∠BAF+∠GAE=90°,
即∠GAF=90°,
∴GA⊥FA.
11.证明:(1)∵∠1=∠2
∴∠1+∠AED=∠2+∠AED,
即∠AEC=∠BED,
在△AEC和△BED中,
,
∴△AEC≌△BED(ASA);
(2)∵△AEC≌△BED,
∴DE=EC,
∴∠EDC=∠C,
∵∠1=∠2=30°,
∴∠C=75°.
12.证明:∵OC平分∠MON,
∴∠AOC=∠BOC,
在△AOC和△BOC中,
,
∴△AOC≌△BOC(SAS).
13.证明:∵C为AE的中点,AE=4,DE=2,
∴AC=AE=2=DE,
又∵DE∥AB,
∴∠BAC=∠E,
在△ABC和△EAD中,,
∴△ABC≌△EAD(AAS).
14.证明:(1)①∵AB=AC,AD=AE,∠BAC=∠DAE=50°,
∴∠ABC=∠ACB=65°,∠ADE=∠AED=65°,∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE;
②∵△BAD≌△CAE,
∴∠ACE=∠ABC=65°,
∴∠ECD=180°﹣∠ACB﹣∠ACE=50°,
(2)∵∠BAC=∠DAE=α,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠ABD,
∵∠BAC=α,AB=AC,
∴∠ABC=∠ACB=,
∴∠ACE=,
∴∠ECD=180°﹣∠ACB﹣∠ACE=α.
15.证明:(1)∵∠BAE=∠BEA,
∴BA=BE,
∵BD为△ABC的角平分线,
∴∠ABD=∠EBC,
在△ABD和△EBC中,
,
∴△ABD≌△EBC(SAS);
(2)由(1)得:△ABD≌△EBC,
∴∠ADB=∠BCE,
∵BD=BC,
∴∠BDC=∠BCD,
又∵∠ADB+∠BDC=180°,
∴∠BCE+∠BCD=180°.
16.证明:(1)∵∠3=∠4,
∴∠ADB=∠ADC,
在△ADB和△ADC中,
,
∴△ADC≌△ADB(ASA),
∴AB=AC;
(2)在△ABC中,AB=AC,∠1=∠2,
∴AE⊥BC.
17.证明:(1)∵AB∥DE,
∴∠CAB=∠E,
在△ABC和△EAD中,
,
∴△ABC≌△EAD(AAS);
(2)∵△ABC≌△EAD,
∴AC=DE=3,AE=AB=7,
∴CE=AE﹣AC=7﹣3=4.
18.证明:在△ACD和△ABE中,
,
∴△ACD≌△ABE(ASA).
∴AD=AE.
∵AB=AC,
∴BD=CE.
在△DOB和△EOC中,
,
∴△DOB≌△EOC(AAS).
19.解:∵BE∥AC,
∴∠E=∠DCO,
在△BOE和△DOC中,,
∴△BOE≌△DOC(AAS),
∴BO=OD,
∵AB=AD,
∴AO平分∠BAC;
20.解:∵AB=AC,∠A=58°,
∴∠B=∠C=(180°﹣∠A)=(180°﹣58°)÷2=61°,
在△DBE和△ECF中,
,
∴△DBE≌△ECF(SAS),
∴∠FEC=∠BDE,
∴∠DEF=180°﹣∠BED﹣∠FEC,
=180°﹣∠DEB﹣∠EDB=∠B=61°.
∵△DBE≌△ECF(SAS),
∴DE=FE,
∴△DEF是等腰三角形,
∴∠EDF=(180°﹣61°)÷2=59.5°.
三角形全等的判定
一.选择题
1.如图,∠ABD=∠EBC,BC=BD,再添加一个条件,使得△ABC≌△EBD,所添加的条件不正确的是( )
A.∠A=∠E
B.BA=BE
C.∠C=∠D
D.AC=DE
2.如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的个数为( )
A.①
B.①②
C.①②③
D.①②④
3.在△ABC中,AB=5,AC=7,则中线AD的取值范围是( )
A.1<AD<7
B.1<AD<8
C.1<AD<6
D.2<AD<5
4.一块三角形玻璃摔成四片(如图),只需带上其中的一片,玻璃店的师傅就能重新配一块与原来形状和大小相同的玻璃,请选出应带玻璃片的序号( )
A.①
B.②
C.③
D.④
5.如图,明明不小心把一块三角形的玻璃打碎成了三块,现要到玻璃店去配一块完全一样的三角形玻璃,则最省事的办法是( )
A.带(1)去
B.带(2)去
C.带(3)去
D.带(1)和(2)去
6.如图,为了测量池塘两岸相对的两点A,B之间的距离,小颖在池塘外取AB的垂线BF上两点C,D,使BC=CD,再画出BF的垂线DE,使点E与A,C在同一条直线上,这时,可得△ABC≌△EDC,因此,测得DE的长就是AB的长.这里判定△ABC≌△EDC的依据是( )
A.ASA
B.SAS
C.AAS
D.SSS
7.如图,已知AB⊥BD,CD⊥BD,AD=BC.判定Rt△ABD和Rt△CDB全等的依据是( )
A.AAS
B.SAS
C.ASA
D.HL
二.填空题
8.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带第
块.
9.在△ABC中,AD⊥BC于D,要用“HL“证明Rt△ADB≌Rt△ADC,则需添加的条件是
.
三.解答题
10.如图,BD、CE是△ABC的高,且BF=AC,CG=AB.探究GA、FA有什么关系?说明理由.
11.如图,∠1=∠2,∠A=∠B,AE=BE,点D在边AC上,AE与BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠2=30°,求∠C的度数.
12.如图,已知OC平分∠MON,点A、B分别在射线OM,ON上,且OA=OB.
求证:△AOC≌△BOC.
13.如图,已知DE∥AB,∠DAE=∠B,DE=2,AE=4,C为AE的中点.
求证:△ABC≌△EAD.
14.如图,AB=AC,AD=AE,∠BAC=∠DAE=50°,点D在BC的延长线上,连接EC.
(1)①求证:BD=CE;
②求∠ECD的度数;
(2)当∠BAC=∠DAE=α时,请直接写出∠ECD的度数.
15.如图,BD为△ABC的角平分线,且BD=BC,E在BD的延长线上,连接AE,∠BAE=∠BEA,连接CE.
求证:
(1)△ABD≌△EBC;
(2)∠BCE+∠BCD=180°.
16.如图,A,D,E三点在同一直线上,∠1=∠2,∠3=∠4.
(1)求证:AB=AC;
(2)求证:AE⊥BC.
17.已知,如图,AB=AE,AB∥DE,∠D=∠ACB.
(1)求证:△ABC≌△EAD;
(2)已知:DE=3,AB=7,求CE的长.
18.如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.CD与BE交于点O.
求证:△DOB≌△EOC.
19.如图,点D是△ABC边AC上一点,AD=AB,过B点作BE∥AD,且BE=CD,连接CE交BD于点O,连接AO.求证:AO平分∠BAC.
20.如图,在△ABC中,AB=AC,∠A=58°,点D、E、F分别在BC、AB、AC边上,且BE=CF,BD=CE,求∠EDF的度数.
参考答案
一.选择题
1.解:∵∠ABC=∠EBD,BC=BD,
∴当添加BA=BE时,可根据“SAS”判断△ABC≌△EBD;
当添加∠C=∠D时,可根据“ASA”判断△ABC≌△EBD;
当添加∠A=∠E时,可根据“AAS”判断△ABC≌△EBD.
故选:D.
2.解:∵∠AOB=∠COD=40°,
∴∠AOB+∠AOD=∠COD+∠AOD,
即∠AOC=∠BOD,
在△AOC和△BOD中,
,
∴△AOC≌△BOD(SAS),
∴∠OCA=∠ODB,∠OAC=∠OBD,AC=BD,①正确;
由三角形的外角性质得:∠AMB+∠OAC=∠AOB+∠OBD,
∴∠AMB=∠AOB=40°,②正确;
作OG⊥MC于G,OH⊥MB于H,如图2所示:
则∠OGC=∠OHD=90°,
在△OCG和△ODH中,
,
∴△OCG≌△ODH(AAS),
∴OG=OH,
∴MO平分∠BMC,④正确;
∵∠AOB=∠COD,
∴当∠DOM=∠AOM时,OM才平分∠BOC,
假设∠DOM=∠AOM,
∵△AOC≌△BOD,
∴∠COM=∠BOM,
∵MO平分∠BMC,
∴∠CMO=∠BMO,
在△COM和△BOM中,
,
∴△COM≌△BOM(ASA),
∴OB=OC,
∵OA=OB,
∴OA=OC,
与OA>OC矛盾,
∴③错误;
正确的有①②④;
故选:D.
3.解:延长AD到E,使AD=DE,连接BE,
∵AD是△ABC的中线,
∴BD=CD,
在△ADC与△EDB中,
,
∴△ADC≌△EDB(SAS),
∴EB=AC,
根据三角形的三边关系得:AC﹣AB<AE<AC+AB,
∴2<AE<12,
∵AE=2AD,
∴1<AD<6,
故选:C.
4.解:由图可知,带2去可以利用“角边角”得到与原三角形全等的三角形.
故选:B.
5.解:根据三角形全等的判定方法,根据角边角可确定一个全等三角形,
只有第三块玻璃包括了两角和它们的夹边,只有带(3)去才能配一块完全一样的玻璃,是符合题意的.
故选:C.
6.解:因为证明在△ABC≌△EDC用到的条件是:BC=CD,∠ABC=∠EDC=90°,∠ACB=∠ECD(对顶角相等),
所以用到的是两角及这两角的夹边对应相等即ASA这一方法.
故选:A.
7.解:∵AB⊥BD,CD⊥BD,
∴∠ABD=∠CDB=90°,
在Rt△ABD和Rt△CDB中,
,
∴Rt△ABD≌Rt△CDB(HL),
故选:D.
二.填空题
8.解:1、2、3块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,
只有第4块有完整的两角及夹边,符合ASA,满足三角形全等的条件,是符合题意的,
故答案为:4.
9.解:添加条件:AB=AC,
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△ABD和Rt△ACD中
,
∴Rt△ABD≌Rt△ACD(HL),
故答案为:AB=AC.
三.解答题
10.解:GA=FA,GA⊥FA,理由如下:
∵BD、CE是△ABC的高,
∴∠ADB=∠AEC=90°,
∴∠ABF+∠BAD=90°∠GCA+∠BAD=90°,
∴∠ABF=∠GCA,
在△ABF和△GCA中,
,
∴△ABF≌△GCA(SAS),
∴FA=GA,∠BAF=∠G,
∵CE是△ABC的高,
∴CE⊥AB,
∴∠G+∠GAE=90°,
∴∠BAF+∠GAE=90°,
即∠GAF=90°,
∴GA⊥FA.
11.证明:(1)∵∠1=∠2
∴∠1+∠AED=∠2+∠AED,
即∠AEC=∠BED,
在△AEC和△BED中,
,
∴△AEC≌△BED(ASA);
(2)∵△AEC≌△BED,
∴DE=EC,
∴∠EDC=∠C,
∵∠1=∠2=30°,
∴∠C=75°.
12.证明:∵OC平分∠MON,
∴∠AOC=∠BOC,
在△AOC和△BOC中,
,
∴△AOC≌△BOC(SAS).
13.证明:∵C为AE的中点,AE=4,DE=2,
∴AC=AE=2=DE,
又∵DE∥AB,
∴∠BAC=∠E,
在△ABC和△EAD中,,
∴△ABC≌△EAD(AAS).
14.证明:(1)①∵AB=AC,AD=AE,∠BAC=∠DAE=50°,
∴∠ABC=∠ACB=65°,∠ADE=∠AED=65°,∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE;
②∵△BAD≌△CAE,
∴∠ACE=∠ABC=65°,
∴∠ECD=180°﹣∠ACB﹣∠ACE=50°,
(2)∵∠BAC=∠DAE=α,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠ABD,
∵∠BAC=α,AB=AC,
∴∠ABC=∠ACB=,
∴∠ACE=,
∴∠ECD=180°﹣∠ACB﹣∠ACE=α.
15.证明:(1)∵∠BAE=∠BEA,
∴BA=BE,
∵BD为△ABC的角平分线,
∴∠ABD=∠EBC,
在△ABD和△EBC中,
,
∴△ABD≌△EBC(SAS);
(2)由(1)得:△ABD≌△EBC,
∴∠ADB=∠BCE,
∵BD=BC,
∴∠BDC=∠BCD,
又∵∠ADB+∠BDC=180°,
∴∠BCE+∠BCD=180°.
16.证明:(1)∵∠3=∠4,
∴∠ADB=∠ADC,
在△ADB和△ADC中,
,
∴△ADC≌△ADB(ASA),
∴AB=AC;
(2)在△ABC中,AB=AC,∠1=∠2,
∴AE⊥BC.
17.证明:(1)∵AB∥DE,
∴∠CAB=∠E,
在△ABC和△EAD中,
,
∴△ABC≌△EAD(AAS);
(2)∵△ABC≌△EAD,
∴AC=DE=3,AE=AB=7,
∴CE=AE﹣AC=7﹣3=4.
18.证明:在△ACD和△ABE中,
,
∴△ACD≌△ABE(ASA).
∴AD=AE.
∵AB=AC,
∴BD=CE.
在△DOB和△EOC中,
,
∴△DOB≌△EOC(AAS).
19.解:∵BE∥AC,
∴∠E=∠DCO,
在△BOE和△DOC中,,
∴△BOE≌△DOC(AAS),
∴BO=OD,
∵AB=AD,
∴AO平分∠BAC;
20.解:∵AB=AC,∠A=58°,
∴∠B=∠C=(180°﹣∠A)=(180°﹣58°)÷2=61°,
在△DBE和△ECF中,
,
∴△DBE≌△ECF(SAS),
∴∠FEC=∠BDE,
∴∠DEF=180°﹣∠BED﹣∠FEC,
=180°﹣∠DEB﹣∠EDB=∠B=61°.
∵△DBE≌△ECF(SAS),
∴DE=FE,
∴△DEF是等腰三角形,
∴∠EDF=(180°﹣61°)÷2=59.5°.
