湖南省醴陵二中、醴陵四中2011-2012学年高二上学期期中联考数学试题
文档属性
| 名称 | 湖南省醴陵二中、醴陵四中2011-2012学年高二上学期期中联考数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 125.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-10 19:41:05 | ||
图片预览

文档简介
醴陵二中、醴陵四中
2011年下学期两校联考高二年级数学期中考试试卷
命题学校:醴陵四中 命题人:曾立霞 审题人:汤金怀
时量:120分钟 总分:150分
A卷
一、选择题(每小题5分,共40分)
1、在△ABC中,若a = 2 ,, , 则B等于( )
A. B.或 C. D.或
2、在数列中,等于( )
A.11 B.12 C.13 D.14
3、等比数列中, 则的前4项和为( )
A. 81 B.120 C.168 D.192
4、已知{an}是等差数列,且a2+ a3+ a8+ a9=48,则a5+ a6= ( )
A.12 B.16 C.20 D.24
5、已知的最小值是( )
A.2 B.1 C.4 D.
6、设,,则下列不等式成立的是( )。
A. B. C. D.
7、已知点(3,1)和(- 4,6)在直线3x-2y+a=0的两侧,则a的取值范围是( )
A. a<-7或 a>24 B. a=7 或 a=24 C. -78、已知{an}是等差数列,( )
A.16 B.24 C.36 D.48
二、填空题(每小题5分,共25分)
9、已知{an}是等差数列,
10、在中, 若,则的外接圆的半径为 _____.
11、若等三角形的周长是底边长的5倍,则它的顶角的余弦值为_________。
12、若不等式的解集是,则的值为________。
13、已知等比数列{an}中,a1+a2=9,a1a2a3=27,则{an}的前n项和 Sn= ___________ 。
三、解答题
14、(11分)已知集合A={x|,其中},B={x|},且AB = R,求实数的取值范围。
15、(12分)已知数列的前项和。
(1)求数列的通项公式; (2)求的最小值。
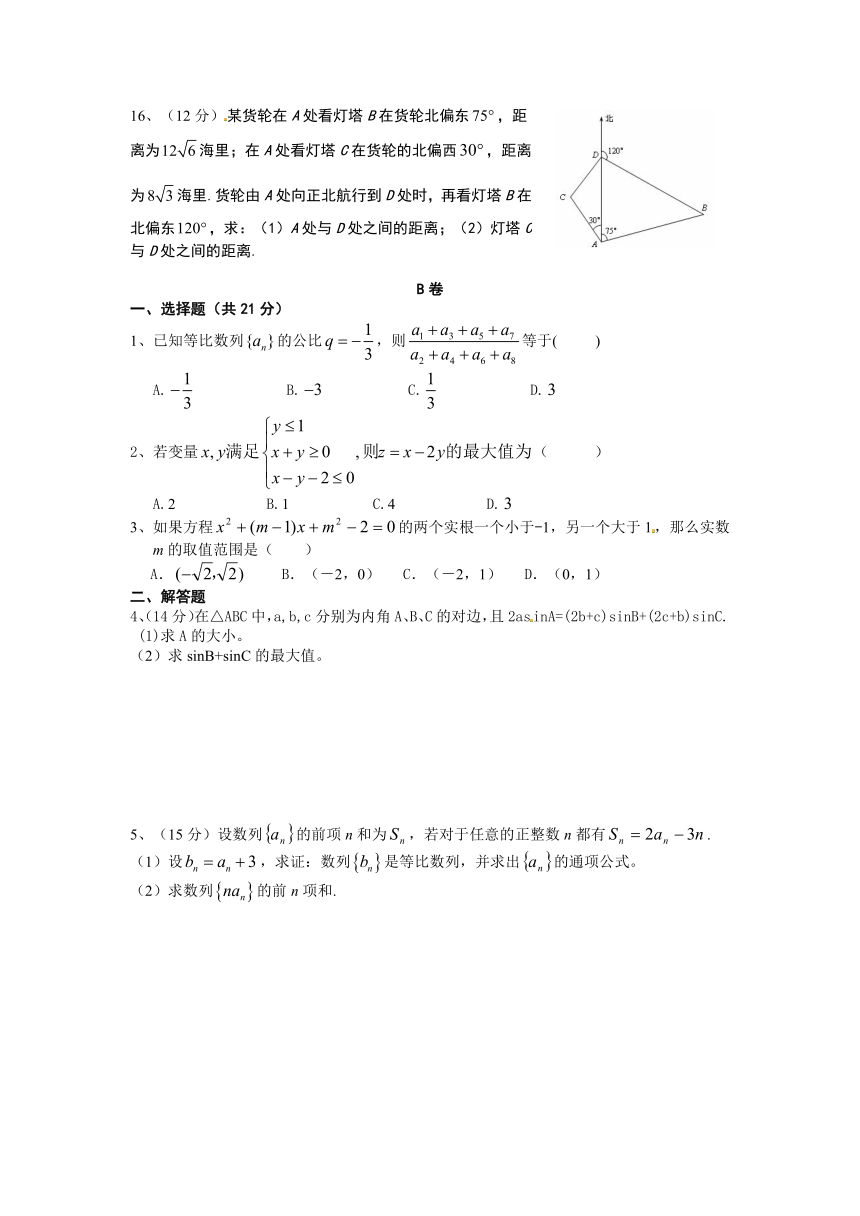
16、(12分)某货轮在A处看灯塔B在货轮北偏东,距离为海里;在A处看灯塔C在货轮的北偏西,距离为海里.货轮由A处向正北航行到D处时,再看灯塔B在北偏东,求:(1)A处与D处之间的距离;(2)灯塔C与D处之间的距离.
B卷
一、选择题(共21分)
1、已知等比数列的公比,则等于( )
A. B. C. D.
2、若变量( )
A.2 B.1 C.4 D.
3、如果方程的两个实根一个小于 1,另一个大于1,那么实数
m的取值范围是( )
A. B.(-2,0) C.(-2,1) D.(0,1)
二、解答题
4、(14分)在△ABC中,a,b,c分别为内角A、B、C的对边,且2asinA=(2b+c)sinB+(2c+b)sinC.
(1)求A的大小。
(2)求sinB+sinC的最大值。
5、(15分)设数列的前项n和为,若对于任意的正整数n都有.
(1)设,求证:数列是等比数列,并求出的通项公式。
(2)求数列的前n项和.
高二数学参考答案
A卷
三、解答题
14.解:∵A={x|},B={x|或},(4分)
又AB = R,
∴(11分)
15.解:(1)
∴(6分)
(2) ∵
∴当n=24时,有最小值:-576(12分)
16.解:(Ⅰ)在△ABD中,由已知得 ∠ADB=,B=.由正弦定理得 . (6分)
(Ⅱ)在△ADC中,由余弦定理得 ,
解得CD=
B卷
1、B 2、D 3、D
5.解:(1)对于任意的正整数都成立,
两式相减,得
∴, 即
,即对一切正整数都成立。
∴数列是等比数列。(5分)
由已知得 即
∴首项,公比,
。。(8分)
2011年下学期两校联考高二年级数学期中考试试卷
命题学校:醴陵四中 命题人:曾立霞 审题人:汤金怀
时量:120分钟 总分:150分
A卷
一、选择题(每小题5分,共40分)
1、在△ABC中,若a = 2 ,, , 则B等于( )
A. B.或 C. D.或
2、在数列中,等于( )
A.11 B.12 C.13 D.14
3、等比数列中, 则的前4项和为( )
A. 81 B.120 C.168 D.192
4、已知{an}是等差数列,且a2+ a3+ a8+ a9=48,则a5+ a6= ( )
A.12 B.16 C.20 D.24
5、已知的最小值是( )
A.2 B.1 C.4 D.
6、设,,则下列不等式成立的是( )。
A. B. C. D.
7、已知点(3,1)和(- 4,6)在直线3x-2y+a=0的两侧,则a的取值范围是( )
A. a<-7或 a>24 B. a=7 或 a=24 C. -7
A.16 B.24 C.36 D.48
二、填空题(每小题5分,共25分)
9、已知{an}是等差数列,
10、在中, 若,则的外接圆的半径为 _____.
11、若等三角形的周长是底边长的5倍,则它的顶角的余弦值为_________。
12、若不等式的解集是,则的值为________。
13、已知等比数列{an}中,a1+a2=9,a1a2a3=27,则{an}的前n项和 Sn= ___________ 。
三、解答题
14、(11分)已知集合A={x|,其中},B={x|},且AB = R,求实数的取值范围。
15、(12分)已知数列的前项和。
(1)求数列的通项公式; (2)求的最小值。
16、(12分)某货轮在A处看灯塔B在货轮北偏东,距离为海里;在A处看灯塔C在货轮的北偏西,距离为海里.货轮由A处向正北航行到D处时,再看灯塔B在北偏东,求:(1)A处与D处之间的距离;(2)灯塔C与D处之间的距离.
B卷
一、选择题(共21分)
1、已知等比数列的公比,则等于( )
A. B. C. D.
2、若变量( )
A.2 B.1 C.4 D.
3、如果方程的两个实根一个小于 1,另一个大于1,那么实数
m的取值范围是( )
A. B.(-2,0) C.(-2,1) D.(0,1)
二、解答题
4、(14分)在△ABC中,a,b,c分别为内角A、B、C的对边,且2asinA=(2b+c)sinB+(2c+b)sinC.
(1)求A的大小。
(2)求sinB+sinC的最大值。
5、(15分)设数列的前项n和为,若对于任意的正整数n都有.
(1)设,求证:数列是等比数列,并求出的通项公式。
(2)求数列的前n项和.
高二数学参考答案
A卷
三、解答题
14.解:∵A={x|},B={x|或},(4分)
又AB = R,
∴(11分)
15.解:(1)
∴(6分)
(2) ∵
∴当n=24时,有最小值:-576(12分)
16.解:(Ⅰ)在△ABD中,由已知得 ∠ADB=,B=.由正弦定理得 . (6分)
(Ⅱ)在△ADC中,由余弦定理得 ,
解得CD=
B卷
1、B 2、D 3、D
5.解:(1)对于任意的正整数都成立,
两式相减,得
∴, 即
,即对一切正整数都成立。
∴数列是等比数列。(5分)
由已知得 即
∴首项,公比,
。。(8分)
同课章节目录
