沪科版数学八年级上期末复习专题:第14章 全等三角形(word版含答案)
文档属性
| 名称 | 沪科版数学八年级上期末复习专题:第14章 全等三角形(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 102.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-12 19:20:03 | ||
图片预览

文档简介
全等三角形
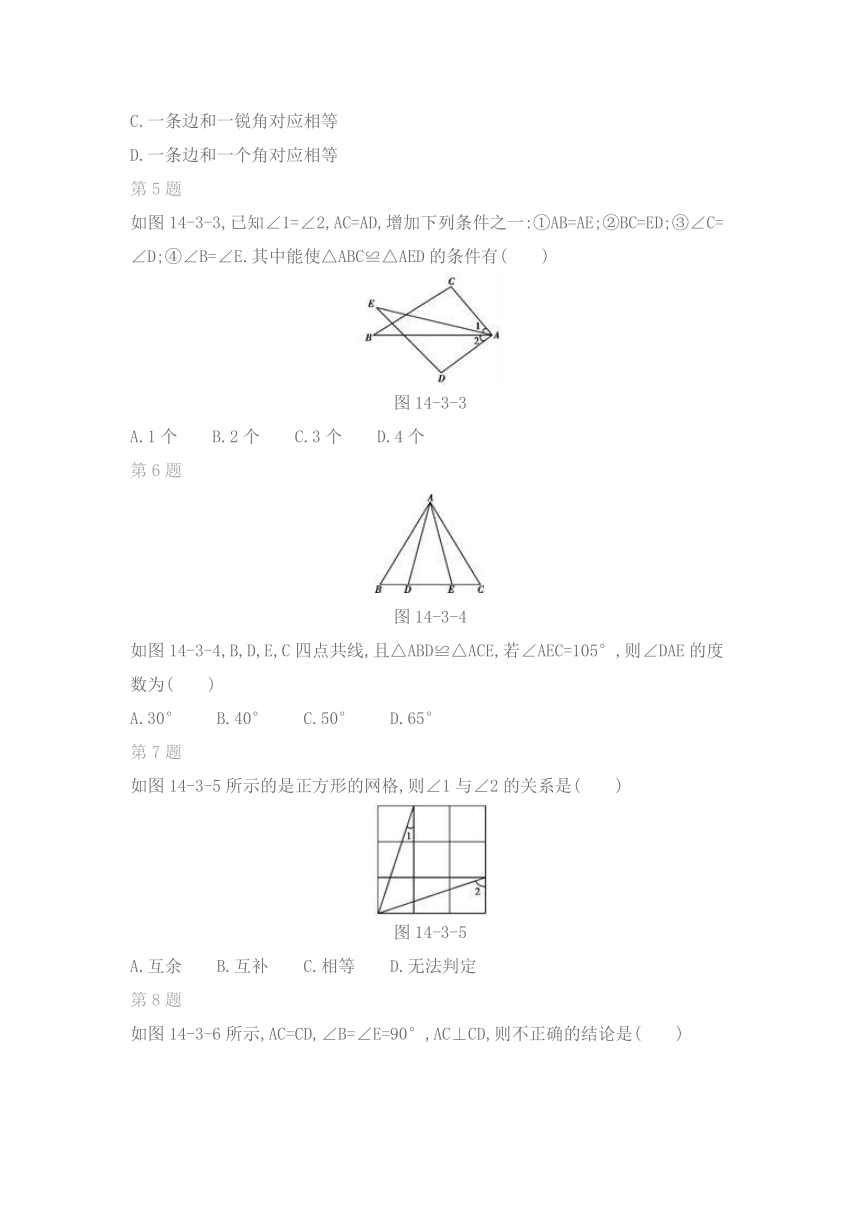
第1题
下列汽车标志中,不是由多个全等图形组成的是( )
第2题
)如图14-3-1,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出了一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )
图14-3-1
A.SSS B.SAS C.AAS D.ASA
第3题
工人师傅常用角尺平分一个任意角.作法如下:如图14-3-2所示,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合.过角尺顶点C的射线OC即是∠AOB的平分线.这种作法的依据是( )
图14-3-2
A.HL B.SSS C.SAS D.ASA
第4题
下列条件中不可以判定两个直角三角形全等的是( )
A.两条直角边对应相等
B.斜边和直角边对应相等
C.一条边和一锐角对应相等
D.一条边和一个角对应相等
第5题
如图14-3-3,已知∠1=∠2,AC=AD,增加下列条件之一:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有( )
图14-3-3
A.1个 B.2个 C.3个 D.4个
第6题
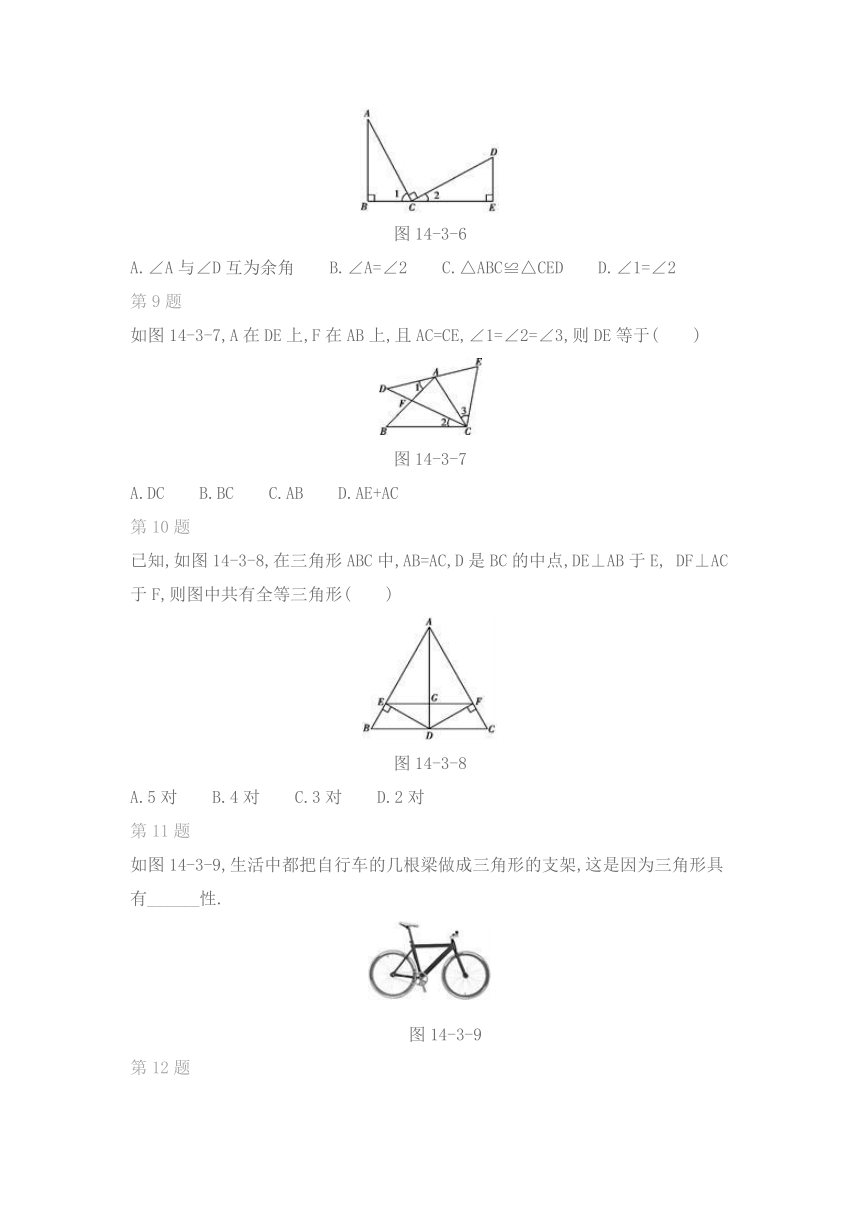
图14-3-4
如图14-3-4,B,D,E,C四点共线,且△ABD≌△ACE,若∠AEC=105°,则∠DAE的度数为( )
A.30° B.40° C.50° D.65°
第7题
如图14-3-5所示的是正方形的网格,则∠1与∠2的关系是( )
图14-3-5
A.互余 B.互补 C.相等 D.无法判定
第8题
如图14-3-6所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
图14-3-6
A.∠A与∠D互为余角 B.∠A=∠2 C.△ABC≌△CED D.∠1=∠2
第9题
如图14-3-7,A在DE上,F在AB上,且AC=CE,∠1=∠2=∠3,则DE等于( )
图14-3-7
A.DC B.BC C.AB D.AE+AC
第10题
已知,如图14-3-8,在三角形ABC中,AB=AC,D是BC的中点,DE⊥AB于E,
DF⊥AC于F,则图中共有全等三角形( )
图14-3-8
A.5对 B.4对 C.3对 D.2对
第11题
如图14-3-9,生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有______性.
图14-3-9
第12题
如图14-3-10,AD和CB相交于点E,BE=DE,请添加一个条件,使△ABE≌△CDE(只添一个即可),你所添加的条件是________.
图14-3-10
第13题
如果△ABC≌△DEF,且△ABC的周长是90
cm,AB=30
cm,DF=20
cm,那么BC的长等于________cm.
第14题
如图14-3-11,△ABC中,∠A=60°,将△ABC沿DE翻折后,点A落在BC边上的点A'处,如果∠A'EC=70°,那么∠A'DE=________.
图14-3-11
第15题
如图14-3-12,在Rt△ABC中,∠ACB=90°,BC=2
cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5
cm,则AE=________cm.
图14-3-12
第16题
如图14-3-13,已知AB=BE,∠1=∠2,∠ADE=120°,AE、BD相交于点F,则∠3的度数为____________.
图14-3-13
第17题
如图14-3-14,已知AB=AC,AE=AF,BE与CF交于点D,则以下结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上,其中正确的是________.(将正确结论的序号都填上)
图14-3-14
第18题
如图14-3-15,已知△ABC中,AB=AC=16
cm,∠B=∠C,BC=10
cm,点D为AB的中点,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当△BPD与△CQP全等时,点Q运动速度为________厘米/秒.
图14-3-15
第19题
如图14-3-16,如果点B,E,C在同一条直线上,∠B=∠C=∠AEF,那么△ABE与△ECF全等吗?若全等,请加以证明;若不全等,请你只补充一个条件,使它们全等,并加以证明.
图14-3-16
第20题
如图14-3-17,线段AB上有点C,D使得AC=BD,过C作CE⊥BE于点E,过D作DF⊥AF于点F,且BE=AF.求证:BE∥AF.
图14-3-17
第21题
如图14-3-18,△ACB≌△ACD,点A、C、E在一条直线上,F、G为边CB和CD上的点,且BF=DG.求证:EF=EG.
图14-3-18
第22题
如图14-3-19,在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.
(1)求证:AD=AG;
(2)AD与AG的位置关系如何?请说明理由.
图14-3-19
第23题
如图14-3-20,在四边形ABDC中,AC=AB,DC=DB,∠CAB=60°,∠CDB=120°,E是AC上一点,F是AB延长线上一点,且CE=BF.
(1)试说明DE=DF;
(2)在图14-3-20中,若G在AB上且∠EDG=60°,试猜想CE、EG、BG之间的数量关系,并证明所归纳的结论;
(3)若题中条件“∠CAB=60°且∠CDB=120°”改为∠CAB=α,∠CDB=180°-α,G在AB上,∠EDG满足什么条件时,(2)中结论仍然成立?
图14-3-20
第1题
下列汽车标志中,不是由多个全等图形组成的是( )
第2题
)如图14-3-1,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出了一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )
图14-3-1
A.SSS B.SAS C.AAS D.ASA
第3题
工人师傅常用角尺平分一个任意角.作法如下:如图14-3-2所示,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合.过角尺顶点C的射线OC即是∠AOB的平分线.这种作法的依据是( )
图14-3-2
A.HL B.SSS C.SAS D.ASA
第4题
下列条件中不可以判定两个直角三角形全等的是( )
A.两条直角边对应相等
B.斜边和直角边对应相等
C.一条边和一锐角对应相等
D.一条边和一个角对应相等
第5题
如图14-3-3,已知∠1=∠2,AC=AD,增加下列条件之一:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有( )
图14-3-3
A.1个 B.2个 C.3个 D.4个
第6题
图14-3-4
如图14-3-4,B,D,E,C四点共线,且△ABD≌△ACE,若∠AEC=105°,则∠DAE的度数为( )
A.30° B.40° C.50° D.65°
第7题
如图14-3-5所示的是正方形的网格,则∠1与∠2的关系是( )
图14-3-5
A.互余 B.互补 C.相等 D.无法判定
第8题
如图14-3-6所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
图14-3-6
A.∠A与∠D互为余角 B.∠A=∠2 C.△ABC≌△CED D.∠1=∠2
第9题
如图14-3-7,A在DE上,F在AB上,且AC=CE,∠1=∠2=∠3,则DE等于( )
图14-3-7
A.DC B.BC C.AB D.AE+AC
第10题
已知,如图14-3-8,在三角形ABC中,AB=AC,D是BC的中点,DE⊥AB于E,
DF⊥AC于F,则图中共有全等三角形( )
图14-3-8
A.5对 B.4对 C.3对 D.2对
第11题
如图14-3-9,生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有______性.
图14-3-9
第12题
如图14-3-10,AD和CB相交于点E,BE=DE,请添加一个条件,使△ABE≌△CDE(只添一个即可),你所添加的条件是________.
图14-3-10
第13题
如果△ABC≌△DEF,且△ABC的周长是90
cm,AB=30
cm,DF=20
cm,那么BC的长等于________cm.
第14题
如图14-3-11,△ABC中,∠A=60°,将△ABC沿DE翻折后,点A落在BC边上的点A'处,如果∠A'EC=70°,那么∠A'DE=________.
图14-3-11
第15题
如图14-3-12,在Rt△ABC中,∠ACB=90°,BC=2
cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5
cm,则AE=________cm.
图14-3-12
第16题
如图14-3-13,已知AB=BE,∠1=∠2,∠ADE=120°,AE、BD相交于点F,则∠3的度数为____________.
图14-3-13
第17题
如图14-3-14,已知AB=AC,AE=AF,BE与CF交于点D,则以下结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上,其中正确的是________.(将正确结论的序号都填上)
图14-3-14
第18题
如图14-3-15,已知△ABC中,AB=AC=16
cm,∠B=∠C,BC=10
cm,点D为AB的中点,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当△BPD与△CQP全等时,点Q运动速度为________厘米/秒.
图14-3-15
第19题
如图14-3-16,如果点B,E,C在同一条直线上,∠B=∠C=∠AEF,那么△ABE与△ECF全等吗?若全等,请加以证明;若不全等,请你只补充一个条件,使它们全等,并加以证明.
图14-3-16
第20题
如图14-3-17,线段AB上有点C,D使得AC=BD,过C作CE⊥BE于点E,过D作DF⊥AF于点F,且BE=AF.求证:BE∥AF.
图14-3-17
第21题
如图14-3-18,△ACB≌△ACD,点A、C、E在一条直线上,F、G为边CB和CD上的点,且BF=DG.求证:EF=EG.
图14-3-18
第22题
如图14-3-19,在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.
(1)求证:AD=AG;
(2)AD与AG的位置关系如何?请说明理由.
图14-3-19
第23题
如图14-3-20,在四边形ABDC中,AC=AB,DC=DB,∠CAB=60°,∠CDB=120°,E是AC上一点,F是AB延长线上一点,且CE=BF.
(1)试说明DE=DF;
(2)在图14-3-20中,若G在AB上且∠EDG=60°,试猜想CE、EG、BG之间的数量关系,并证明所归纳的结论;
(3)若题中条件“∠CAB=60°且∠CDB=120°”改为∠CAB=α,∠CDB=180°-α,G在AB上,∠EDG满足什么条件时,(2)中结论仍然成立?
图14-3-20
