人教版七年级数学上学期《4.3.3 余角和补角》 同步练习(word解析版)
文档属性
| 名称 | 人教版七年级数学上学期《4.3.3 余角和补角》 同步练习(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 114.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览




文档简介
4.3.3 余角和补角
一.选择题
1.若∠A=60°,则∠A的补角是它余角的( )
A.2倍 B.3倍 C.4倍 D.5倍
2.一个角的补角为144°,那么这个角的余角是( )
A.36° B.44° C.54° D.126°
3.已知∠A=55°34′,则∠A的余角等于( )
A.44°26′ B.44°56′ C.34°56′ D.34°26′
4.若一个角的补角等于它的余角的3倍,则这个角为( )
A.75° B.60° C.45° D.30°
5.如图,∠AOC=∠BOD=90°,则∠AOB与∠COD的关系是( )
A.相等 B.互余 C.互补 D.不确定
6.如图,将一副三角板如图放置,∠COD=20°,则∠AOB的度数为( )
A.140° B.150° C.160° D.170°
7.如图,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOC+∠DOB的度数为( )
A.90° B.135° C.150° D.180°
8.如果将一副三角板按如图方式摆放,使∠1=15°,那么∠AOB的度数是( )
A.140° B.150° C.160° D.165°
二.填空题
9.若∠1+∠2=90°,∠1+∠3=90°,则∠2=∠3,其根据是 .
10.如图,∠AOC与∠BOD都是直角,且∠AOB:∠AOD=2:7,则∠AOB等于 度.
11.一个角的余角比它的补角的少15°,则这个角为 .
12.若∠1+∠2=180°,∠2+∠3=180°,则∠1与∠3的关系是 ,理由是 .
三.解答题
13.如图所示,∠AOC和∠BOD都是直角.
(1)填空:图中与∠BOC互余的角有 和 ;
(2)∠AOD与∠BOC互补吗?为什么?
(3)若∠AOB:∠AOD=3:13,求∠BOC与∠AOD的度数
14.如图,OD平分∠BOC,OE平分∠AOC.若∠BOC=70°,∠AOC=50°.
(1)求出∠AOB及其补角的度数;
(2)请求出∠DOC和∠AOE的度数,并判断∠DOE与∠AOB是否互补,并说明理由.
15.如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)填空:与∠AOE互补的角有 ;
(2)若∠COD=30°,求∠DOE的度数;
(3)当∠AOD=α°时,请直接写出∠DOE的度数.
16.如图,已知O为直线AD上一点,∠AOC与∠AOB互补,OM和ON分别是∠AOC和∠AOB的平分线.
(1)试说明:∠AOB=∠COD;
(2)若∠COD=36°,求∠MON的度数.
17.已知一个角的补角比这个角的4倍大15°,求这个角的余角.
18.如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°,试求∠AOC与∠AOB的度数.
19.如图,已知∠AOB=140°,∠COE与∠EOD互余,OE平分∠AOD.
(1)若∠COE=40°,则∠DOE= ,∠BOD= ;
(2)设∠COE=α,∠BOD=β,请探究α与β之间的数量关系.
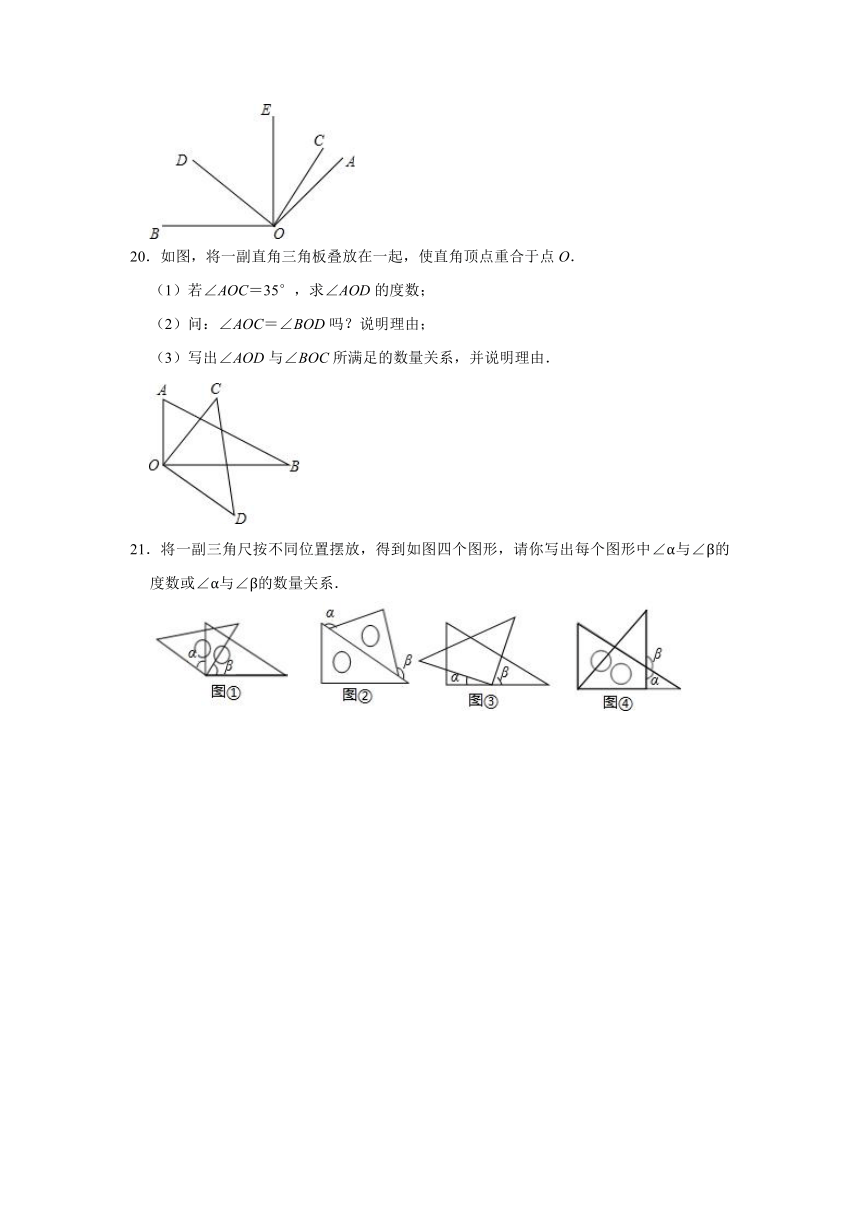
20.如图,将一副直角三角板叠放在一起,使直角顶点重合于点O.
(1)若∠AOC=35°,求∠AOD的度数;
(2)问:∠AOC=∠BOD吗?说明理由;
(3)写出∠AOD与∠BOC所满足的数量关系,并说明理由.
21.将一副三角尺按不同位置摆放,得到如图四个图形,请你写出每个图形中∠α与∠β的度数或∠α与∠β的数量关系.
参考答案
一.选择题
1.解:∠A的补角为:180°﹣60°=120°;
∠A的余角为:90°﹣60°=30°;
120°÷30°=4.
故选:C.
2.解:这个角=180°﹣144°=36°.
这个角的余角=90°﹣36°=54°.
故选:C.
3.解:∵∠A=55°34′,
∴∠A的余角为:90°﹣55°34′=34°26′.
故选:D.
4.解:设这个角为x,则余角为90°﹣x,补角为180°﹣x,
由题意得,180°﹣x=3(90°﹣x),
解得:x=45.
故选:C.
5.解:∵∠AOB+∠BOC=∠COD+∠BOC=90°,
∴∠AOB=∠COD.
故选:A.
6.解:∵∠COD=20°,
∴∠COA=90°﹣20°=70°,
∴∠AOB=∠BOC+∠COA=90°+70°=160°.
故选:C.
7.解:∠AOC+∠DOB
=∠AOB+∠BOC+∠DOB
=∠AOB+∠COD
=90°+90°
=180°.
故选:D.
8.解:∵∠1+∠2=90°,∠1=15°,
∴∠2=75°,
∴∠AOB=∠AOC+∠2=90°+75°=165°.
故选:D.
二.填空题
9.解:若∠1+∠2=90°,∠1+∠3=90°,则∠2=∠3,其根据是同角的余角相等.
故答案为:同角的余角相等
10.解:设∠AOB=x,则∠AOD=90°+x,
∵∠AOB:∠AOD=2:7,
∴=,
解得:x=36°.
故答案为:36.
11.解:设这个角度为x,则
90°﹣x=(180°﹣x)﹣15°,
解得:x=30°.
故答案为:30°.
12.解:∵∠1+∠2=180°,∠2+∠3=180°,
∴∠1=∠3(同角的补角相等),
故答案为:∠1=∠3,同角的补角相等.
三.解答题
13.解:(1)因为∠AOC和∠BOD都是直角,
所以∠AOB+∠BOC=∠COD+∠BOC=90°,
所以∠BOC与∠AOB互余,∠BOC与∠COD互余,
故答案为:∠AOB、∠COD;
(2)∠AOD与∠BOC互补,理由如下:
因为∠AOC和∠BOD都是直角,
所以∠AOB+∠BOC=∠COD+∠BOC=90°,
又因为∠AOD=∠AOB+∠BOC+∠COD,
所以∠AOD+∠BOC=∠AOB+∠BOC+∠COD+∠BOC=180°,
所以∠AOD与∠BOC互补;
(3)设∠AOB=3x°、则∠AOD=13x°,
所以∠BOD=∠AOD﹣∠AOB=13x﹣3x=10x=90,
即x=9,
所以∠AOD=13x=117°,
由(2)可知∠AOD与∠BOC互补,
所以∠BOC=180°﹣117°=63°.
14.解:(1)∠AOB=∠BOC+∠AOC=70°+50°=120°,
其补角为180°﹣∠AOB=180°﹣120°=60°;
(2)∠DOC=×∠BOC=×70°=35°
∠AOE=×∠AOC=×50°=25°.
∠DOE与∠AOB互补,
理由:∵∠DOE=∠DOC+∠COE=35°+25°=60°,
∴∠DOE+∠AOB=60°+120°=180°,
故∠DOE与∠AOB互补.
15.解:(1)∵OE平分∠BOC,
∴∠BOE=∠COE;
∵∠AOE+∠BOE=180°,
∴∠AOE+∠COE=180°,
∴与∠AOE互补的角是∠BOE、∠COE;
故答案为∠BOE、∠COE;
(2)∵OD、OE分别平分∠AOC、∠BOC,
∴∠COD=∠AOD=30°,∠COE=∠BOE=∠BOC,
∴∠AOC=2×30°=60°,
∴∠BOC=180°﹣60°=120°,
∴∠COE=∠BOC=60°,
∴∠DOE=∠COD+∠COE=90°;
(3)当∠AOD=α°时,∠DOE=90°.
16.解:(1)∵∠AOC与∠AOB互补,
∴∠AOC+∠AOB=180°,
∵∠AOC+∠DOC=180°,
∴∠COD=∠AOB;
(2)∵∠AOB=∠COD=36°,
∴∠AOC=180°﹣∠COD=144°,
∵OM和ON分别是∠AOC和∠AOB的平分线,
∴∠AOM==72°,∠AON=,
∴∠MON=∠AOM﹣∠AON=72°﹣18°=54°.
17.解:设这个角为x°,则这个角的补角为(180﹣x)°,
依题意得:(180﹣x)﹣4x=15°,
解得:x=33°,
∴90°﹣x°=57°.
答:这个角的余角是57°.
18.解:设∠AOB=x°,因为∠AOC与∠AOB互补,则∠AOC=180°﹣x°.
由题意,得.
∴180﹣x﹣x=80,
∴﹣2x=﹣100,
解得x=50
故∠AOB=50°,∠AOC=130°.
19.解:(1)∵∠COE与∠EOD互余,∠COE=40°,
∴∠EOD=90°﹣40°=50°,
∵OE平分∠AOD,
∴∠AOD=2∠AOE=100°,
∴∠BOD=∠AOB﹣∠AOD=40°,
故答案为:50°;40°;
(2)∵∠COE=α,且∠COE与∠EOD互余,
∴∠EOD=90°﹣α,
∵OE平分∠AOD
∴∠AOD=2(900﹣α),
∴β+2(900﹣α)=1400
解得,β=2α﹣40°.
20.解:(1)∵∠COD=90°,∠AOC=35°,
∴∠AOD=∠AOC+∠COD=35°+90°=125°;
(2)∠AOC=∠BOD,
理由是:∵∠AOB=∠COD=90°,
∴∠AOB﹣∠COB=∠COD﹣∠COB,
∴∠AOC=∠BOD;
(3)∠AOD+∠BOC=180°,
理由是:∵∠AOB=∠COD=90°,
∴∠AOD+∠BOC
=∠AOC+∠COD+∠BOC
=∠COD+∠AOB
=90°+90°
=180°.
21.解:标出部分角的序号,如图所示.
图①:∵∠α+∠1=90°,∠β+∠1=90°,
∴∠α=∠β.
图②:∵∠α+∠2=180°,∠β+∠3=180°,∠2=60°,∠3=30°,
∴∠α=120°,∠β=150°.
图③:∵∠α+∠4+∠β=180°,∠4=90°,
∴∠α+∠β=90°.
图④:∵∠α+∠β=180°,∠α=60°,
∴∠β=120°.
一.选择题
1.若∠A=60°,则∠A的补角是它余角的( )
A.2倍 B.3倍 C.4倍 D.5倍
2.一个角的补角为144°,那么这个角的余角是( )
A.36° B.44° C.54° D.126°
3.已知∠A=55°34′,则∠A的余角等于( )
A.44°26′ B.44°56′ C.34°56′ D.34°26′
4.若一个角的补角等于它的余角的3倍,则这个角为( )
A.75° B.60° C.45° D.30°
5.如图,∠AOC=∠BOD=90°,则∠AOB与∠COD的关系是( )
A.相等 B.互余 C.互补 D.不确定
6.如图,将一副三角板如图放置,∠COD=20°,则∠AOB的度数为( )
A.140° B.150° C.160° D.170°
7.如图,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOC+∠DOB的度数为( )
A.90° B.135° C.150° D.180°
8.如果将一副三角板按如图方式摆放,使∠1=15°,那么∠AOB的度数是( )
A.140° B.150° C.160° D.165°
二.填空题
9.若∠1+∠2=90°,∠1+∠3=90°,则∠2=∠3,其根据是 .
10.如图,∠AOC与∠BOD都是直角,且∠AOB:∠AOD=2:7,则∠AOB等于 度.
11.一个角的余角比它的补角的少15°,则这个角为 .
12.若∠1+∠2=180°,∠2+∠3=180°,则∠1与∠3的关系是 ,理由是 .
三.解答题
13.如图所示,∠AOC和∠BOD都是直角.
(1)填空:图中与∠BOC互余的角有 和 ;
(2)∠AOD与∠BOC互补吗?为什么?
(3)若∠AOB:∠AOD=3:13,求∠BOC与∠AOD的度数
14.如图,OD平分∠BOC,OE平分∠AOC.若∠BOC=70°,∠AOC=50°.
(1)求出∠AOB及其补角的度数;
(2)请求出∠DOC和∠AOE的度数,并判断∠DOE与∠AOB是否互补,并说明理由.
15.如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)填空:与∠AOE互补的角有 ;
(2)若∠COD=30°,求∠DOE的度数;
(3)当∠AOD=α°时,请直接写出∠DOE的度数.
16.如图,已知O为直线AD上一点,∠AOC与∠AOB互补,OM和ON分别是∠AOC和∠AOB的平分线.
(1)试说明:∠AOB=∠COD;
(2)若∠COD=36°,求∠MON的度数.
17.已知一个角的补角比这个角的4倍大15°,求这个角的余角.
18.如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°,试求∠AOC与∠AOB的度数.
19.如图,已知∠AOB=140°,∠COE与∠EOD互余,OE平分∠AOD.
(1)若∠COE=40°,则∠DOE= ,∠BOD= ;
(2)设∠COE=α,∠BOD=β,请探究α与β之间的数量关系.
20.如图,将一副直角三角板叠放在一起,使直角顶点重合于点O.
(1)若∠AOC=35°,求∠AOD的度数;
(2)问:∠AOC=∠BOD吗?说明理由;
(3)写出∠AOD与∠BOC所满足的数量关系,并说明理由.
21.将一副三角尺按不同位置摆放,得到如图四个图形,请你写出每个图形中∠α与∠β的度数或∠α与∠β的数量关系.
参考答案
一.选择题
1.解:∠A的补角为:180°﹣60°=120°;
∠A的余角为:90°﹣60°=30°;
120°÷30°=4.
故选:C.
2.解:这个角=180°﹣144°=36°.
这个角的余角=90°﹣36°=54°.
故选:C.
3.解:∵∠A=55°34′,
∴∠A的余角为:90°﹣55°34′=34°26′.
故选:D.
4.解:设这个角为x,则余角为90°﹣x,补角为180°﹣x,
由题意得,180°﹣x=3(90°﹣x),
解得:x=45.
故选:C.
5.解:∵∠AOB+∠BOC=∠COD+∠BOC=90°,
∴∠AOB=∠COD.
故选:A.
6.解:∵∠COD=20°,
∴∠COA=90°﹣20°=70°,
∴∠AOB=∠BOC+∠COA=90°+70°=160°.
故选:C.
7.解:∠AOC+∠DOB
=∠AOB+∠BOC+∠DOB
=∠AOB+∠COD
=90°+90°
=180°.
故选:D.
8.解:∵∠1+∠2=90°,∠1=15°,
∴∠2=75°,
∴∠AOB=∠AOC+∠2=90°+75°=165°.
故选:D.
二.填空题
9.解:若∠1+∠2=90°,∠1+∠3=90°,则∠2=∠3,其根据是同角的余角相等.
故答案为:同角的余角相等
10.解:设∠AOB=x,则∠AOD=90°+x,
∵∠AOB:∠AOD=2:7,
∴=,
解得:x=36°.
故答案为:36.
11.解:设这个角度为x,则
90°﹣x=(180°﹣x)﹣15°,
解得:x=30°.
故答案为:30°.
12.解:∵∠1+∠2=180°,∠2+∠3=180°,
∴∠1=∠3(同角的补角相等),
故答案为:∠1=∠3,同角的补角相等.
三.解答题
13.解:(1)因为∠AOC和∠BOD都是直角,
所以∠AOB+∠BOC=∠COD+∠BOC=90°,
所以∠BOC与∠AOB互余,∠BOC与∠COD互余,
故答案为:∠AOB、∠COD;
(2)∠AOD与∠BOC互补,理由如下:
因为∠AOC和∠BOD都是直角,
所以∠AOB+∠BOC=∠COD+∠BOC=90°,
又因为∠AOD=∠AOB+∠BOC+∠COD,
所以∠AOD+∠BOC=∠AOB+∠BOC+∠COD+∠BOC=180°,
所以∠AOD与∠BOC互补;
(3)设∠AOB=3x°、则∠AOD=13x°,
所以∠BOD=∠AOD﹣∠AOB=13x﹣3x=10x=90,
即x=9,
所以∠AOD=13x=117°,
由(2)可知∠AOD与∠BOC互补,
所以∠BOC=180°﹣117°=63°.
14.解:(1)∠AOB=∠BOC+∠AOC=70°+50°=120°,
其补角为180°﹣∠AOB=180°﹣120°=60°;
(2)∠DOC=×∠BOC=×70°=35°
∠AOE=×∠AOC=×50°=25°.
∠DOE与∠AOB互补,
理由:∵∠DOE=∠DOC+∠COE=35°+25°=60°,
∴∠DOE+∠AOB=60°+120°=180°,
故∠DOE与∠AOB互补.
15.解:(1)∵OE平分∠BOC,
∴∠BOE=∠COE;
∵∠AOE+∠BOE=180°,
∴∠AOE+∠COE=180°,
∴与∠AOE互补的角是∠BOE、∠COE;
故答案为∠BOE、∠COE;
(2)∵OD、OE分别平分∠AOC、∠BOC,
∴∠COD=∠AOD=30°,∠COE=∠BOE=∠BOC,
∴∠AOC=2×30°=60°,
∴∠BOC=180°﹣60°=120°,
∴∠COE=∠BOC=60°,
∴∠DOE=∠COD+∠COE=90°;
(3)当∠AOD=α°时,∠DOE=90°.
16.解:(1)∵∠AOC与∠AOB互补,
∴∠AOC+∠AOB=180°,
∵∠AOC+∠DOC=180°,
∴∠COD=∠AOB;
(2)∵∠AOB=∠COD=36°,
∴∠AOC=180°﹣∠COD=144°,
∵OM和ON分别是∠AOC和∠AOB的平分线,
∴∠AOM==72°,∠AON=,
∴∠MON=∠AOM﹣∠AON=72°﹣18°=54°.
17.解:设这个角为x°,则这个角的补角为(180﹣x)°,
依题意得:(180﹣x)﹣4x=15°,
解得:x=33°,
∴90°﹣x°=57°.
答:这个角的余角是57°.
18.解:设∠AOB=x°,因为∠AOC与∠AOB互补,则∠AOC=180°﹣x°.
由题意,得.
∴180﹣x﹣x=80,
∴﹣2x=﹣100,
解得x=50
故∠AOB=50°,∠AOC=130°.
19.解:(1)∵∠COE与∠EOD互余,∠COE=40°,
∴∠EOD=90°﹣40°=50°,
∵OE平分∠AOD,
∴∠AOD=2∠AOE=100°,
∴∠BOD=∠AOB﹣∠AOD=40°,
故答案为:50°;40°;
(2)∵∠COE=α,且∠COE与∠EOD互余,
∴∠EOD=90°﹣α,
∵OE平分∠AOD
∴∠AOD=2(900﹣α),
∴β+2(900﹣α)=1400
解得,β=2α﹣40°.
20.解:(1)∵∠COD=90°,∠AOC=35°,
∴∠AOD=∠AOC+∠COD=35°+90°=125°;
(2)∠AOC=∠BOD,
理由是:∵∠AOB=∠COD=90°,
∴∠AOB﹣∠COB=∠COD﹣∠COB,
∴∠AOC=∠BOD;
(3)∠AOD+∠BOC=180°,
理由是:∵∠AOB=∠COD=90°,
∴∠AOD+∠BOC
=∠AOC+∠COD+∠BOC
=∠COD+∠AOB
=90°+90°
=180°.
21.解:标出部分角的序号,如图所示.
图①:∵∠α+∠1=90°,∠β+∠1=90°,
∴∠α=∠β.
图②:∵∠α+∠2=180°,∠β+∠3=180°,∠2=60°,∠3=30°,
∴∠α=120°,∠β=150°.
图③:∵∠α+∠4+∠β=180°,∠4=90°,
∴∠α+∠β=90°.
图④:∵∠α+∠β=180°,∠α=60°,
∴∠β=120°.
