沪教版(上海)数学八年级第二学期-22.5 (1)等腰梯形的性质 课件共15张ppt
文档属性
| 名称 | 沪教版(上海)数学八年级第二学期-22.5 (1)等腰梯形的性质 课件共15张ppt |

|
|
| 格式 | pptx | ||
| 文件大小 | 122.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览




文档简介
22.5(1)等腰梯形的性质
(1) 什么是梯形?
(2) 什么是等腰梯形?
温故知新
猜想:等腰梯形有哪些性质?
边:
等腰梯形两底平行,
两腰相等.
角:
等腰梯形在同一条底上的两个内角相等.
对角线:
等腰梯形的两条对角线相等.
对称性:
等腰梯形是轴对称图形.
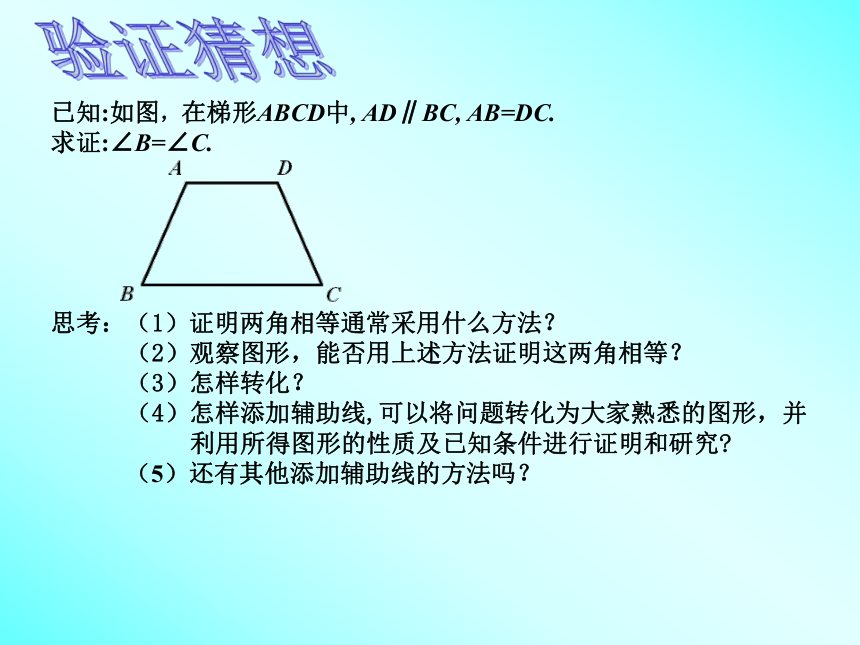
已知:如图,在梯形ABCD中, AD∥BC, AB=DC.
求证:∠B=∠C.
思考:(1)证明两角相等通常采用什么方法?
(2)观察图形,能否用上述方法证明这两角相等?
(3)怎样转化?
(4)怎样添加辅助线,可以将问题转化为大家熟悉的图形,并
利用所得图形的性质及已知条件进行证明和研究?
(5)还有其他添加辅助线的方法吗?
验证猜想
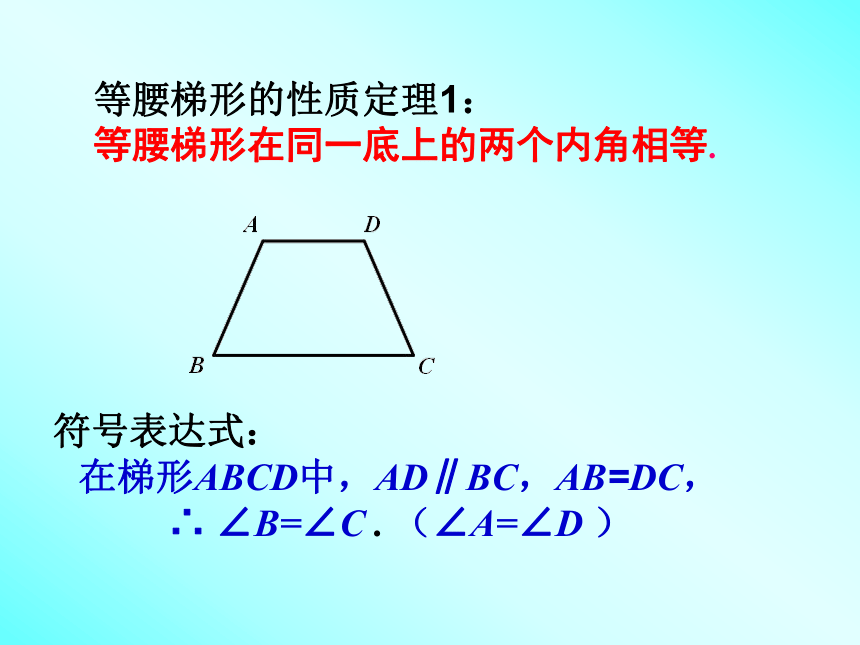
等腰梯形的性质定理1:
等腰梯形在同一底上的两个内角相等.
符号表达式:
在梯形ABCD中,AD∥BC,AB=DC,
∴ ∠B=∠C . (∠A=∠D )
例题1
已知:如图,等腰梯形ABCD,AD∥BC,腰BA和CD的延长线相交于点E.
求证:△EAD是等腰三角形.
思考:若作∠E的角平分线,你能得出什么结论?
等腰梯形是一个轴对称图形,对称轴是两底的中点的连线所在的直线.
例题讲解
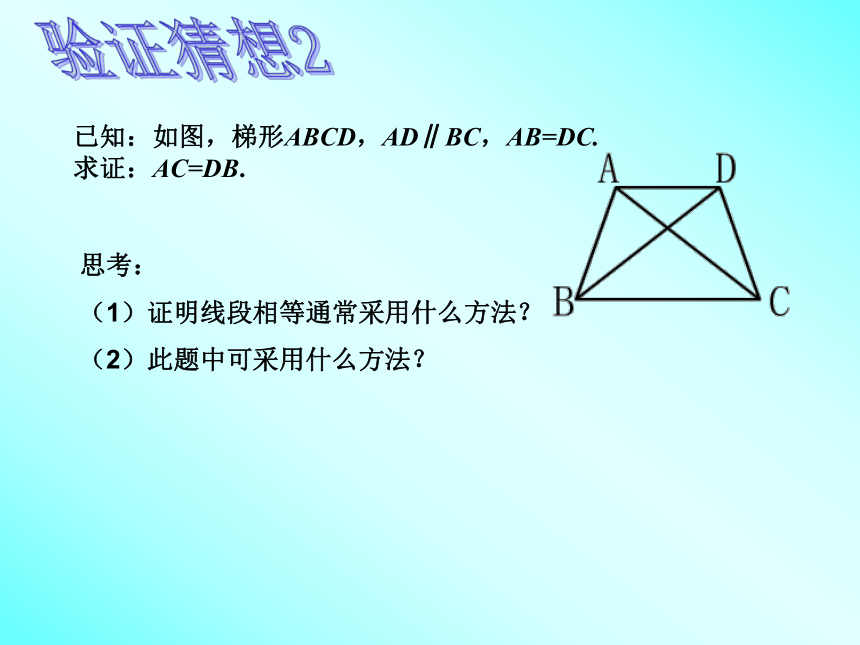
已知:如图,梯形ABCD,AD∥BC,AB=DC.
求证:AC=DB.
思考:
(1)证明线段相等通常采用什么方法?
(2)此题中可采用什么方法?
验证猜想2
等腰梯形的性质定理2:
等腰梯形的对角线相等.
符号表达式:
在梯形ABCD中,AD∥BC,AB=DC,
∴ AC=BD .
例题2
如图,已知等腰梯形中,AD∥BC,AD=10cm,BC=20cm,
对角线AC=17 cm,求梯形ABCD的面积.
思考:
(1)梯形面积计算公式是什么?
(2)如何求梯形的高?
(3)四边形ACED是一个什么四边形?
△DBE是一个什么三角形?
(4)还有其他方法吗?
例题讲解
1.已知等腰梯形的一个内角是55°,则其他三个角为________.
2.已知:如图,等腰梯形ABCD,AD∥BC,∠ABC=60°,
AD=15,AB=45. 求BC的长. (看谁的方法多!)
小试牛刀
一.等腰梯形的性质
1.等腰梯形在_________的两个内角__________.
2.等腰梯形的对角线____________.
3.等腰梯形是_________图形,
对称轴是______________________________.
二.梯形问题中常添的辅助线
课内小结
同一底上
相等
相等
轴对称
两底的中点的连线所在的直线
1.如图,在等腰梯形ABCD中, AD∥BC, AD=AB, BD⊥DC.
求: ∠C的度数.
试一试
解: 在等腰梯形ABCD中, AD∥BC, AD=AB
∴∠ABC=∠C(等腰梯形在同一底上的两个内角相等)
∵ AD∥BC ∴∠ADB=∠DBC
∵ AD=AB ∴∠ADB=∠ABD
∴∠DBC =∠ABD
设∠DBC 的度数为x,则∠ABC的度数为2x, ∠C的度数为2x.
在Rt△ DBC中, ∠DBC + ∠C=90,
即x+ 2x=90,得x=30
∴ ∠C=60 °.
2. 已知等腰梯形的上、下底边长分别是2cm, 8cm,
腰长是5cm, 求高.
解:过点A、D作AE⊥BC,DF⊥BC,垂足分别为E、F
则AE∥ DF 又 AD∥ BC
∴AE=DF, AD=EF=2
又∵AB=CD
∴Rt△ABE≌ Rt△DCF (H.L)
∴BE=CF=3
在Rt△ABE中,
即这个等腰梯形的高为4cm.
作业布置
练习册:习题22.5(1)
谢谢!
(1) 什么是梯形?
(2) 什么是等腰梯形?
温故知新
猜想:等腰梯形有哪些性质?
边:
等腰梯形两底平行,
两腰相等.
角:
等腰梯形在同一条底上的两个内角相等.
对角线:
等腰梯形的两条对角线相等.
对称性:
等腰梯形是轴对称图形.
已知:如图,在梯形ABCD中, AD∥BC, AB=DC.
求证:∠B=∠C.
思考:(1)证明两角相等通常采用什么方法?
(2)观察图形,能否用上述方法证明这两角相等?
(3)怎样转化?
(4)怎样添加辅助线,可以将问题转化为大家熟悉的图形,并
利用所得图形的性质及已知条件进行证明和研究?
(5)还有其他添加辅助线的方法吗?
验证猜想
等腰梯形的性质定理1:
等腰梯形在同一底上的两个内角相等.
符号表达式:
在梯形ABCD中,AD∥BC,AB=DC,
∴ ∠B=∠C . (∠A=∠D )
例题1
已知:如图,等腰梯形ABCD,AD∥BC,腰BA和CD的延长线相交于点E.
求证:△EAD是等腰三角形.
思考:若作∠E的角平分线,你能得出什么结论?
等腰梯形是一个轴对称图形,对称轴是两底的中点的连线所在的直线.
例题讲解
已知:如图,梯形ABCD,AD∥BC,AB=DC.
求证:AC=DB.
思考:
(1)证明线段相等通常采用什么方法?
(2)此题中可采用什么方法?
验证猜想2
等腰梯形的性质定理2:
等腰梯形的对角线相等.
符号表达式:
在梯形ABCD中,AD∥BC,AB=DC,
∴ AC=BD .
例题2
如图,已知等腰梯形中,AD∥BC,AD=10cm,BC=20cm,
对角线AC=17 cm,求梯形ABCD的面积.
思考:
(1)梯形面积计算公式是什么?
(2)如何求梯形的高?
(3)四边形ACED是一个什么四边形?
△DBE是一个什么三角形?
(4)还有其他方法吗?
例题讲解
1.已知等腰梯形的一个内角是55°,则其他三个角为________.
2.已知:如图,等腰梯形ABCD,AD∥BC,∠ABC=60°,
AD=15,AB=45. 求BC的长. (看谁的方法多!)
小试牛刀
一.等腰梯形的性质
1.等腰梯形在_________的两个内角__________.
2.等腰梯形的对角线____________.
3.等腰梯形是_________图形,
对称轴是______________________________.
二.梯形问题中常添的辅助线
课内小结
同一底上
相等
相等
轴对称
两底的中点的连线所在的直线
1.如图,在等腰梯形ABCD中, AD∥BC, AD=AB, BD⊥DC.
求: ∠C的度数.
试一试
解: 在等腰梯形ABCD中, AD∥BC, AD=AB
∴∠ABC=∠C(等腰梯形在同一底上的两个内角相等)
∵ AD∥BC ∴∠ADB=∠DBC
∵ AD=AB ∴∠ADB=∠ABD
∴∠DBC =∠ABD
设∠DBC 的度数为x,则∠ABC的度数为2x, ∠C的度数为2x.
在Rt△ DBC中, ∠DBC + ∠C=90,
即x+ 2x=90,得x=30
∴ ∠C=60 °.
2. 已知等腰梯形的上、下底边长分别是2cm, 8cm,
腰长是5cm, 求高.
解:过点A、D作AE⊥BC,DF⊥BC,垂足分别为E、F
则AE∥ DF 又 AD∥ BC
∴AE=DF, AD=EF=2
又∵AB=CD
∴Rt△ABE≌ Rt△DCF (H.L)
∴BE=CF=3
在Rt△ABE中,
即这个等腰梯形的高为4cm.
作业布置
练习册:习题22.5(1)
谢谢!
