沪教版(上海)数学八年级第二学期-22.5 梯形复习 课件(共15张ppt)
文档属性
| 名称 | 沪教版(上海)数学八年级第二学期-22.5 梯形复习 课件(共15张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 216.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览




文档简介
梯形复习
一.知识梳理
1、梯形:是指一组对边 而另一组对边
的四边形;
或指一组对边 且 的四边形。
2、特殊的梯形有: 、 。
3、梯形的中位线:连接梯形两腰的 的 线段。梯形中位线的长度等于 。
平行
不平行
平行
不相等
等腰梯形
直角梯形
中点
两底和的一半
4.等腰梯形的性质与判定:
边的关系
角的关系
对角线
对称性
性质
两底
2.两腰
同一底上的两个角
2.不在同一底上的角
两条对角线
对称图形。
判定
两腰 的梯形
同一底上的两个
角 的梯形
两条对角线 的梯形
相等
平行
相等
互补
相等
轴
相等
相等
相等
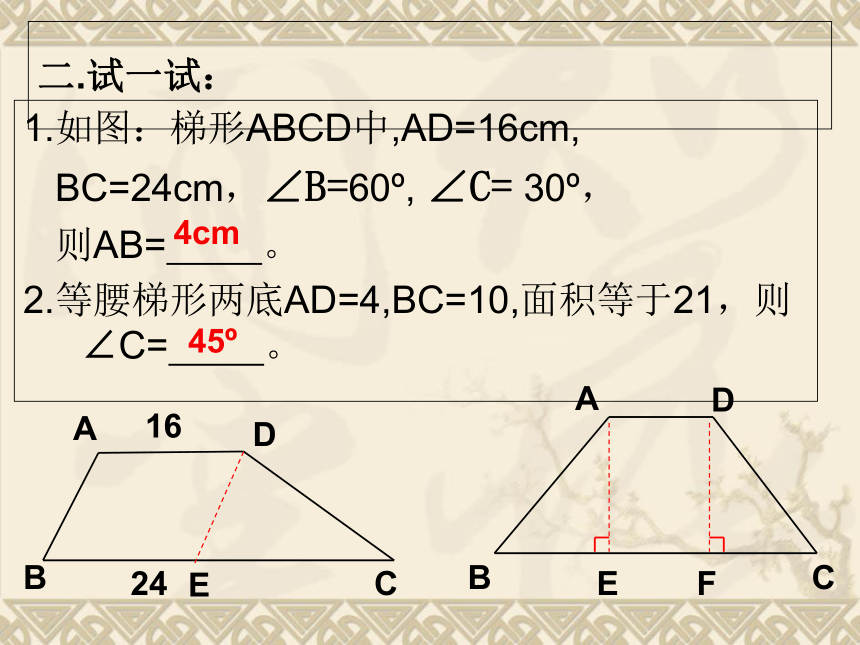
二.试一试:
1.如图:梯形ABCD中,AD=16cm,
BC=24cm,∠B=60?, ∠C= 30?,
则AB= 。
2.等腰梯形两底AD=4,BC=10,面积等于21,则∠C= 。
4cm
45?
A
B
E
D
16
24
A
D
C
B
C
E
F
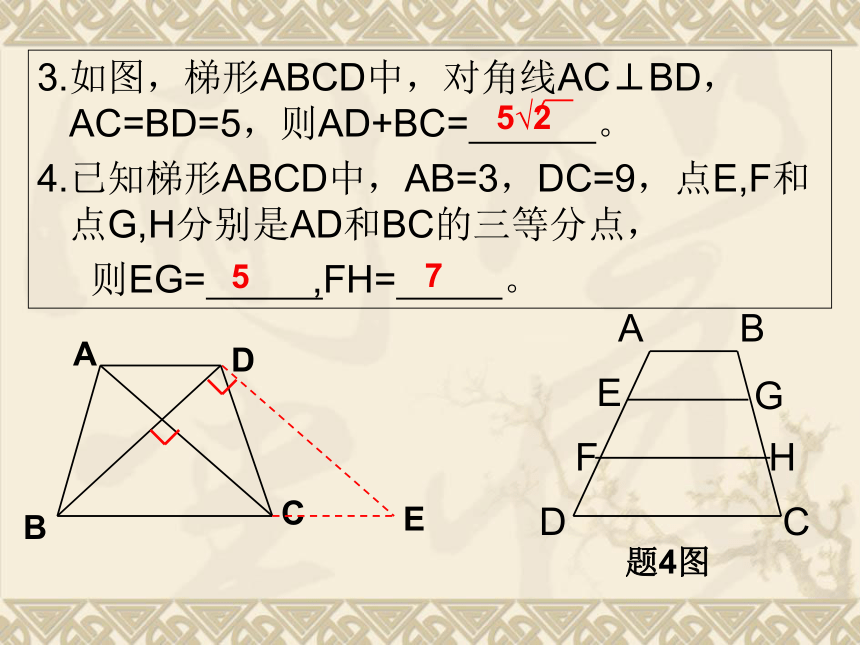
3.如图,梯形ABCD中,对角线AC⊥BD,AC=BD=5,则AD+BC= 。
4.已知梯形ABCD中,AB=3,DC=9,点E,F和点G,H分别是AD和BC的三等分点,
则EG= ,FH= 。
5
7
A
B
C
D
E
G
F
H
题4图
5√2
A
B
D
C
E
适时小结:
1.常用的梯形辅助线的做法有:
平移腰
作高
平移对角线
延长两腰交与一点
2.梯形问题
转化
或
的问题。
平行四边形
三角形
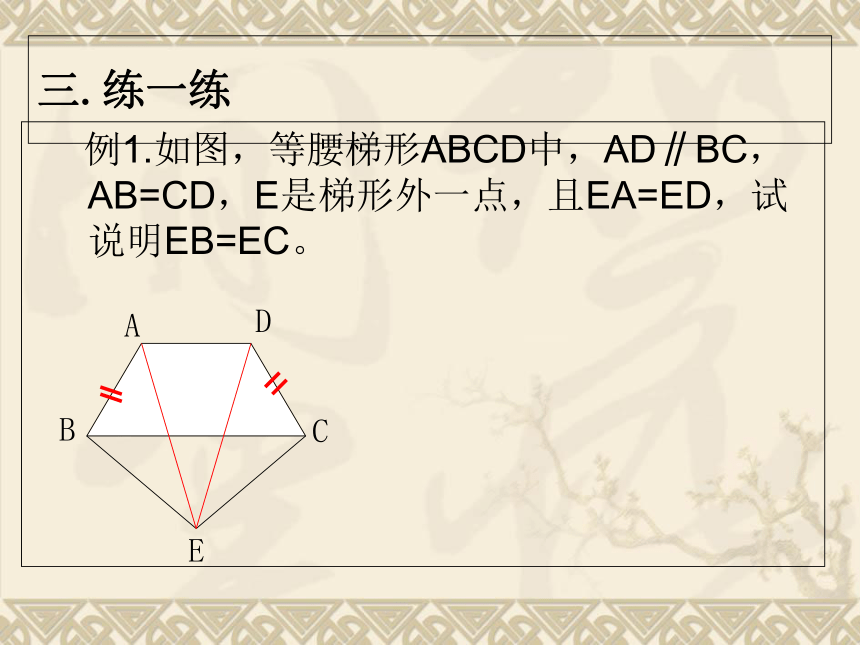
三.练一练
例1.如图,等腰梯形ABCD中,AD∥BC,AB=CD,E是梯形外一点,且EA=ED,试说明EB=EC。
E
B
D
C
A
例2、在梯形ABCD中,AB∥CD,AC、BD相交于点O,如果OA=OB, 试说明梯形ABCD是等腰梯形。
C
O
D
B
A
在已知四边形是梯形的情况下,要证明是等腰梯形,可以从哪些方面考虑?
1.已知梯形ABCD中,AD ∥BC,E是AB中点,DE和CE分别平分∠ADC和∠BCD。
求证:AD+BC=CD
B
D
C
E
A
分析:
1)梯形+腰上中点,联想到什么?
2)从图形的运动角度考虑,看到中点,想到什么?看到角平分线,想到什么?
梯形的中位线
图形的旋转与翻折
四.拓展应用
已知:如图,梯形ABCD中,AB∥CD,M、N分别为CD、AB的中点,且∠A+∠ B=90°
求证:
方法一:平移两腰
证明:过点M作ME∥AD交AB于E,MF∥BC交AB于F.
∵AB ∥CD, ME∥AD
∴四边形AEMD是平行四边形
∴ AE=DM
同理可得: BF=CM.
∴EF=AB-AE-BF=AB-AD.
∵ ME∥AD , MF∥BC
∴ ∠A=∠1, ∠B=∠2,
又∵∠A+∠B=90°,
∴∠1+∠2=90°.
∴△MEF是直角三角形.
∵M、N分别是CD、AB中点
∴DM=CM,AN=BN
又∵ AE=DM , BF=CM
∴ EN=FN
在Rt△MEF中,EN=FN, N是EF的中点
∴MN= EF
即
方法二:延长两腰交与一点
O
证明:延长AB,DC交与点O,连接MO
∵∠A+∠B=90°
∴∠AOB= 90°
即△AOB,△DOC是直角三角形
在直角三角形△ AOB中,N是AB中点
∴ON=AN= AB
∴∠A= ∠AON
同理可得:
OM=DN= DC
∠ODM= ∠DOM
∵AB∥CD
∴ ∠A= ∠ODM
∴ ∠AON= ∠DOM
∵点A,D,O在同一直线上
∴点O,M,N在同一直线上
∵MN=ON-OM
∴2MN=AB-CD
∴
O
反思:为什么要证明点O,M,N在一直线上?不证明行不行?
小结
1.梯形的概念、及分类
2.等腰梯形的性质及判定
3.梯形解题中常添加的辅助线
作业布置
完成学习单上余下作业
一.知识梳理
1、梯形:是指一组对边 而另一组对边
的四边形;
或指一组对边 且 的四边形。
2、特殊的梯形有: 、 。
3、梯形的中位线:连接梯形两腰的 的 线段。梯形中位线的长度等于 。
平行
不平行
平行
不相等
等腰梯形
直角梯形
中点
两底和的一半
4.等腰梯形的性质与判定:
边的关系
角的关系
对角线
对称性
性质
两底
2.两腰
同一底上的两个角
2.不在同一底上的角
两条对角线
对称图形。
判定
两腰 的梯形
同一底上的两个
角 的梯形
两条对角线 的梯形
相等
平行
相等
互补
相等
轴
相等
相等
相等
二.试一试:
1.如图:梯形ABCD中,AD=16cm,
BC=24cm,∠B=60?, ∠C= 30?,
则AB= 。
2.等腰梯形两底AD=4,BC=10,面积等于21,则∠C= 。
4cm
45?
A
B
E
D
16
24
A
D
C
B
C
E
F
3.如图,梯形ABCD中,对角线AC⊥BD,AC=BD=5,则AD+BC= 。
4.已知梯形ABCD中,AB=3,DC=9,点E,F和点G,H分别是AD和BC的三等分点,
则EG= ,FH= 。
5
7
A
B
C
D
E
G
F
H
题4图
5√2
A
B
D
C
E
适时小结:
1.常用的梯形辅助线的做法有:
平移腰
作高
平移对角线
延长两腰交与一点
2.梯形问题
转化
或
的问题。
平行四边形
三角形
三.练一练
例1.如图,等腰梯形ABCD中,AD∥BC,AB=CD,E是梯形外一点,且EA=ED,试说明EB=EC。
E
B
D
C
A
例2、在梯形ABCD中,AB∥CD,AC、BD相交于点O,如果OA=OB, 试说明梯形ABCD是等腰梯形。
C
O
D
B
A
在已知四边形是梯形的情况下,要证明是等腰梯形,可以从哪些方面考虑?
1.已知梯形ABCD中,AD ∥BC,E是AB中点,DE和CE分别平分∠ADC和∠BCD。
求证:AD+BC=CD
B
D
C
E
A
分析:
1)梯形+腰上中点,联想到什么?
2)从图形的运动角度考虑,看到中点,想到什么?看到角平分线,想到什么?
梯形的中位线
图形的旋转与翻折
四.拓展应用
已知:如图,梯形ABCD中,AB∥CD,M、N分别为CD、AB的中点,且∠A+∠ B=90°
求证:
方法一:平移两腰
证明:过点M作ME∥AD交AB于E,MF∥BC交AB于F.
∵AB ∥CD, ME∥AD
∴四边形AEMD是平行四边形
∴ AE=DM
同理可得: BF=CM.
∴EF=AB-AE-BF=AB-AD.
∵ ME∥AD , MF∥BC
∴ ∠A=∠1, ∠B=∠2,
又∵∠A+∠B=90°,
∴∠1+∠2=90°.
∴△MEF是直角三角形.
∵M、N分别是CD、AB中点
∴DM=CM,AN=BN
又∵ AE=DM , BF=CM
∴ EN=FN
在Rt△MEF中,EN=FN, N是EF的中点
∴MN= EF
即
方法二:延长两腰交与一点
O
证明:延长AB,DC交与点O,连接MO
∵∠A+∠B=90°
∴∠AOB= 90°
即△AOB,△DOC是直角三角形
在直角三角形△ AOB中,N是AB中点
∴ON=AN= AB
∴∠A= ∠AON
同理可得:
OM=DN= DC
∠ODM= ∠DOM
∵AB∥CD
∴ ∠A= ∠ODM
∴ ∠AON= ∠DOM
∵点A,D,O在同一直线上
∴点O,M,N在同一直线上
∵MN=ON-OM
∴2MN=AB-CD
∴
O
反思:为什么要证明点O,M,N在一直线上?不证明行不行?
小结
1.梯形的概念、及分类
2.等腰梯形的性质及判定
3.梯形解题中常添加的辅助线
作业布置
完成学习单上余下作业
