人教版七年级上册数学课件:4.3.1角(共40张ppt)
文档属性
| 名称 | 人教版七年级上册数学课件:4.3.1角(共40张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览







文档简介
4.3.1角与角的度量(1)
4.3角
习目学标
1.角的定义(静态的定义,动态的定义)
及平角、周角的形成概念
2.角的表示方法(四种方法)。
3.角的测量方法及度量工具(量角器)
的用法;
4.角的基本换算单位及进制(60进制);
说一说生活中的角
??[想一想]角是由两条怎样的线组成的图形?
用一句话概括什么样的图形叫做角。
试一试,你行吗?
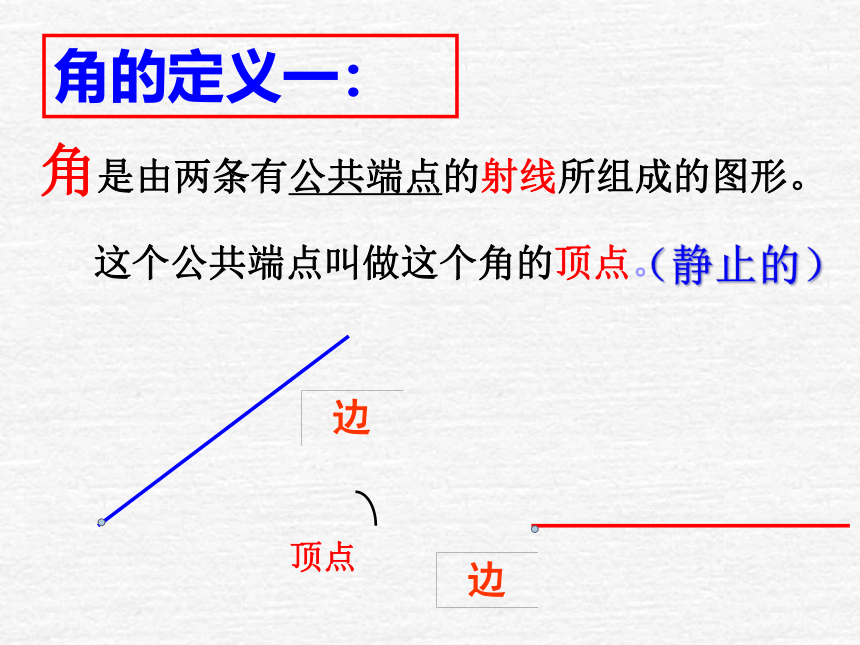
定义:
边
边
角的主要特征:
一个公共端点、两条射线。
角是由两条具有公共端点的射线组成的图形。
角是由两条有公共端点的射线所组成的图形。
这个公共端点叫做这个角的顶点。
角的定义一:
顶点
(静止的)
边
边
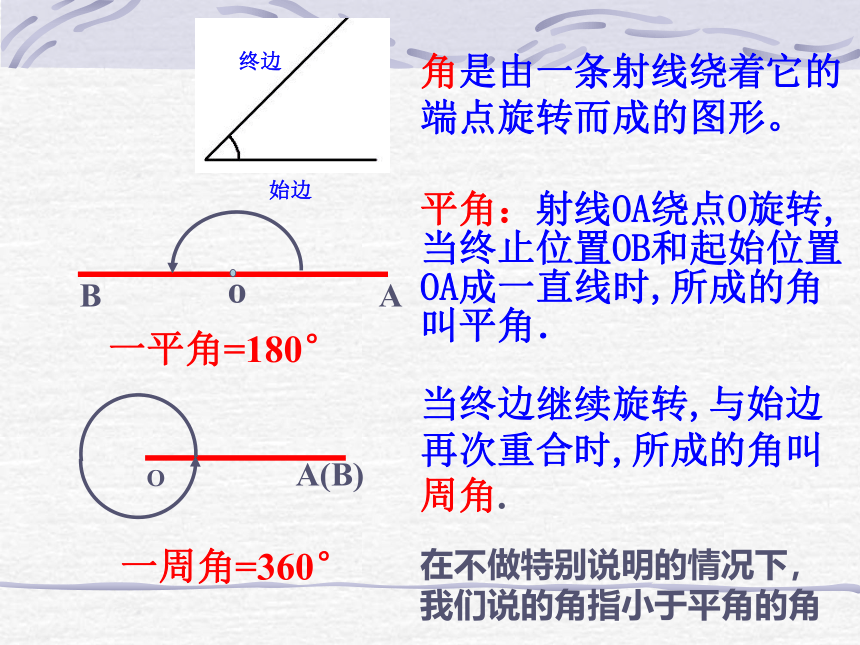
角是由一条射线绕着它的端点旋转而成的图形。
始边
终边
平角:射线OA绕点O旋转,当终止位置OB和起始位置OA成一直线时,所成的角叫平角.
o
A
B
当终边继续旋转,与始边再次重合时,所成的角叫周角.
O
A(B)
一平角=180°
一周角=360°
在不做特别说明的情况下,我们说的角指小于平角的角
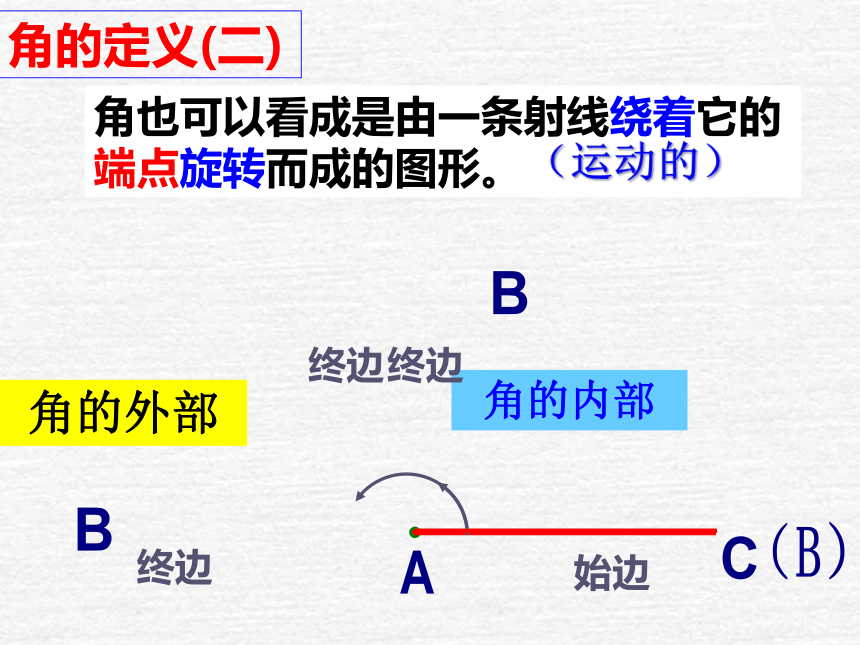
角也可以看成是由一条射线绕着它的端点旋转而成的图形。
角的定义(二)
角的内部
角的外部
(运动的)
C
A
始边
终边
B
终边
终边
B
(B)
角的表示:
1、角用符号“ ”表示,读作“角”。
2、表示角的方法:
A
B
C
1
a
B
C
A
D
图1
图2
写作:∠ABC或∠CBA
∠ a 和∠1
注意:顶点字母写在中间。
读做:角ABC或角CBA
A
B
C
D
O
1
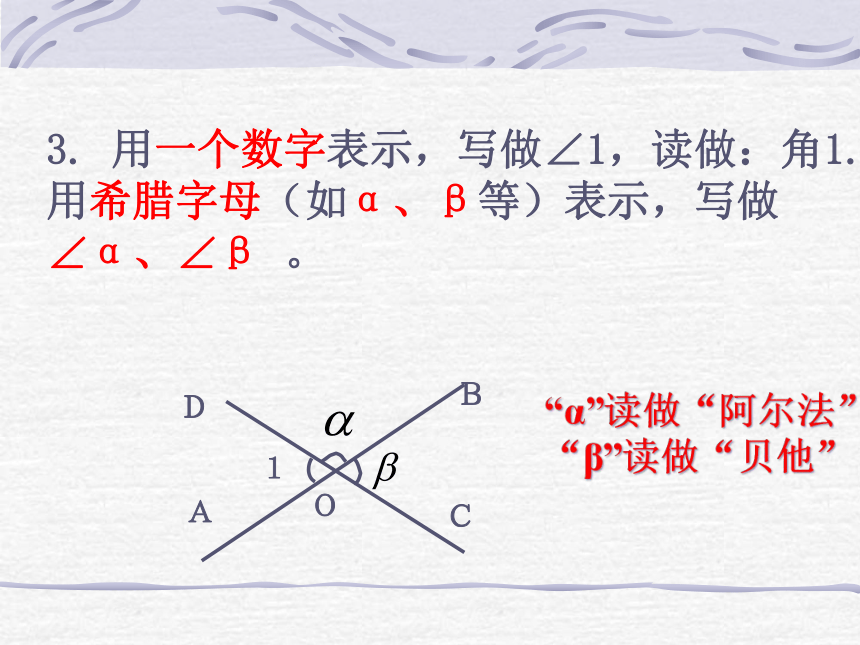
3. 用一个数字表示,写做∠1,读做:角1.
用希腊字母(如α、β等)表示,写做
∠α、∠β 。
“α”读做“阿尔法”
“β”读做“贝他”
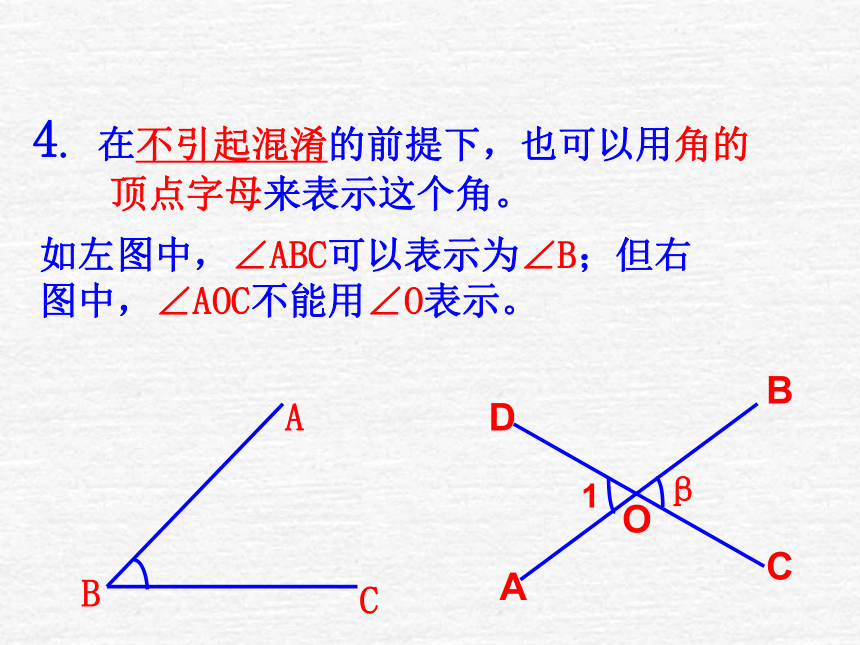
4. 在不引起混淆的前提下,也可以用角的
顶点字母来表示这个角。
如左图中,∠ABC可以表示为∠B;但右
图中,∠AOC不能用∠O表示。
B
C
A
A
B
C
D
1
β
O
3.角的四种表示方法
表示方法
注意事项
1、用三个大写的
字母表示
表示顶点的字母
要写在中间
2、用一个顶点的
字母来表示
一个字母只表
示一个角
3、用一个数字
在靠近顶点的处画上
弧线,并写上数字
4、希腊字母表示
在靠近顶点的处画上弧
线,并写上希腊字母
归纳
练习
1、图中有 个角,分别是 .
3
∠AOB、∠AOC、∠BOC
2、将图中的角用不同的方法表示出来,并填写下表:
∠1
∠β
∠BCE
∠ACB
∠BAC
∠ABC
A
B
C
D
E
1
2
α
β
∠α
∠2
∠BAD
∠B
考考你
写出图中,(l)能用一个字母表示的角.(2)以B为顶点的角.(3)图中共有几个角(小于平角).
A
C
B
D
图中有多少个角?请用适当的方式把它们表示出来。
想一想:
平角:一条射线绕着端点旋转,旋转到和始边成一条直线时所成的角。
B
O
A
平角的度数为1800
周角:一条射线绕着端点旋转,旋转到终边和始边重合时所成的角。
(无特别说明,我们只讨论大于0°小于180°的角)
(B)
A
O
周角的度数为3600
三个城市相应钟表上时针与分针所成角的度数分别为多少?
巴黎时间 北京时间 东京时间
30°
120°
90°
我能行,我可以
钟表的时针从午夜零时到早上6时转成一个什么角?
(平角)
钟表的时针从午夜零时到中午12时转成一个什么角?
(周角)
合作学习:
(2)任意画出一个角,再用量角器量一量。在测量中,你遇到哪些问题?
观察图中的量角器,并讨论下列问题:
(1)量角器上的平角被等分成多少个1°的角
A
1、对“中”——角的顶点与量角器的中心重合
2、对线 ——角的一边与量角器的零线重合
3、读数 ——读出角的另一边所对的度数
对中 对线 读数
度量角的方法:
发现:角只用“度”作单位是不够的!
人们还规定了分、秒作为角的度量单位
度、分、秒是角的基本度量单位.
50
1°的 为1分,
1
60
记作 1′,
即1°=( )′
记作 1″,
即1′=( ) ″
1′=( )°
1
60
1 ″=( )′
1
60
1′的 为1秒,
1
60
60
60
角的基本度量单位:
1. 度、分、秒是角的基本度量单位。
2. 度分秒之间的互化:
1? 的角 等分成60份 1′的角
1?的角 等分成60份 1 ?? 的角
1°= ____″
3600
注意:度分秒是60进制的
例1、
把23°36′化成用度表示的角.
解:先把36 ′化成度,即
36 ′=(36÷60)°=0.6 °
所以 23°36′=23.6 °
例题精析
例2、
解:因为1°=60′,所以
0.12°= 60′× 0.12=7.2′
又因为 1′=60? ,
所以 0.2 ′=60? ×0.2=12?
因此 95.12°=95 °7′12?
把95.12°化成用度、分、秒表示的角
例题精析
解:
例3、计算
例题精析
1.用度、分、秒表示:
⑴0.75°= ′= ″
⑵(-)°= ′= ″
⑶16.24°= ° ′ ″
4
15
45
2700
16
960
16
14
24
2.用度表示:
⑴1800″= ′=________°
(2)50°40 ′30 ″= 50°__ ′=______°
30
0.5
40.5
50.675
比一比谁算得快
1、用度、分、秒表示48.32°
2、用度表示30°9'36"
练一练
解:∵0.36°=0.36×60′=19.2′
0.2′=0.2×60″=12″
∴48.32°=48°19′12″
解:∵9′=(9÷60)°=0.15°
36″=(36÷3600)°=0.01°
∴30°9′36″=30°+0.15°+0.01°=30.16°
°
基本步骤 :先把秒化成分,并与原有的分合并,再化成度。
练一练
练一练
思考题
180°–(45°17′+52°57′)
解: 原式
= 180°–97°74′
= 180°–98°14′
= 179°60′–98°14′
= 81°46′
辩一辩
如果两个角的度数一个为18.15?,一个为18?15′,它们一样大吗?
注意:计算时,算式的单位要一致。
1.角的两种定义;
2.角的四种表示方法;
3.角的测量方法;
畅谈所得 感悟提升
本节收获知多少?
简单小小角,一点两条边,
取名要慎重,顶点夹中间.
分秒换算须注意,每逢六十才进一.
画它要牢记,先点再画边.
莫把“∠”相忘
字母数字前,
思考题:1.数一数下面一共有几角?
一共有 6个角
O
A
B
C
D
课后拓展
3条射线
4条射线
5条射线
6条射线
B
F
K
P
3条射线时有___个角;4条射线时有___个角,
5条射线有____个角;6条射线时有___个角;
那么n条射线时有___________个角。
课后拓展
思考题:2.看图填空:
O
O
∠AOB内射线条数
1
2
3
4
…
99
…
n
角的个数
3.根据所给的图形填写下表
静态定义
动态定义
角
定义
表示法
角的测量
与换算
用三个
大写字母
用数字或
希腊字母
用顶点字
母表示
角度制
的换算
角的和
差运算
角的和
差运算
归纳
下课了!
再见!
Thank you!
4.3角
习目学标
1.角的定义(静态的定义,动态的定义)
及平角、周角的形成概念
2.角的表示方法(四种方法)。
3.角的测量方法及度量工具(量角器)
的用法;
4.角的基本换算单位及进制(60进制);
说一说生活中的角
??[想一想]角是由两条怎样的线组成的图形?
用一句话概括什么样的图形叫做角。
试一试,你行吗?
定义:
边
边
角的主要特征:
一个公共端点、两条射线。
角是由两条具有公共端点的射线组成的图形。
角是由两条有公共端点的射线所组成的图形。
这个公共端点叫做这个角的顶点。
角的定义一:
顶点
(静止的)
边
边
角是由一条射线绕着它的端点旋转而成的图形。
始边
终边
平角:射线OA绕点O旋转,当终止位置OB和起始位置OA成一直线时,所成的角叫平角.
o
A
B
当终边继续旋转,与始边再次重合时,所成的角叫周角.
O
A(B)
一平角=180°
一周角=360°
在不做特别说明的情况下,我们说的角指小于平角的角
角也可以看成是由一条射线绕着它的端点旋转而成的图形。
角的定义(二)
角的内部
角的外部
(运动的)
C
A
始边
终边
B
终边
终边
B
(B)
角的表示:
1、角用符号“ ”表示,读作“角”。
2、表示角的方法:
A
B
C
1
a
B
C
A
D
图1
图2
写作:∠ABC或∠CBA
∠ a 和∠1
注意:顶点字母写在中间。
读做:角ABC或角CBA
A
B
C
D
O
1
3. 用一个数字表示,写做∠1,读做:角1.
用希腊字母(如α、β等)表示,写做
∠α、∠β 。
“α”读做“阿尔法”
“β”读做“贝他”
4. 在不引起混淆的前提下,也可以用角的
顶点字母来表示这个角。
如左图中,∠ABC可以表示为∠B;但右
图中,∠AOC不能用∠O表示。
B
C
A
A
B
C
D
1
β
O
3.角的四种表示方法
表示方法
注意事项
1、用三个大写的
字母表示
表示顶点的字母
要写在中间
2、用一个顶点的
字母来表示
一个字母只表
示一个角
3、用一个数字
在靠近顶点的处画上
弧线,并写上数字
4、希腊字母表示
在靠近顶点的处画上弧
线,并写上希腊字母
归纳
练习
1、图中有 个角,分别是 .
3
∠AOB、∠AOC、∠BOC
2、将图中的角用不同的方法表示出来,并填写下表:
∠1
∠β
∠BCE
∠ACB
∠BAC
∠ABC
A
B
C
D
E
1
2
α
β
∠α
∠2
∠BAD
∠B
考考你
写出图中,(l)能用一个字母表示的角.(2)以B为顶点的角.(3)图中共有几个角(小于平角).
A
C
B
D
图中有多少个角?请用适当的方式把它们表示出来。
想一想:
平角:一条射线绕着端点旋转,旋转到和始边成一条直线时所成的角。
B
O
A
平角的度数为1800
周角:一条射线绕着端点旋转,旋转到终边和始边重合时所成的角。
(无特别说明,我们只讨论大于0°小于180°的角)
(B)
A
O
周角的度数为3600
三个城市相应钟表上时针与分针所成角的度数分别为多少?
巴黎时间 北京时间 东京时间
30°
120°
90°
我能行,我可以
钟表的时针从午夜零时到早上6时转成一个什么角?
(平角)
钟表的时针从午夜零时到中午12时转成一个什么角?
(周角)
合作学习:
(2)任意画出一个角,再用量角器量一量。在测量中,你遇到哪些问题?
观察图中的量角器,并讨论下列问题:
(1)量角器上的平角被等分成多少个1°的角
A
1、对“中”——角的顶点与量角器的中心重合
2、对线 ——角的一边与量角器的零线重合
3、读数 ——读出角的另一边所对的度数
对中 对线 读数
度量角的方法:
发现:角只用“度”作单位是不够的!
人们还规定了分、秒作为角的度量单位
度、分、秒是角的基本度量单位.
50
1°的 为1分,
1
60
记作 1′,
即1°=( )′
记作 1″,
即1′=( ) ″
1′=( )°
1
60
1 ″=( )′
1
60
1′的 为1秒,
1
60
60
60
角的基本度量单位:
1. 度、分、秒是角的基本度量单位。
2. 度分秒之间的互化:
1? 的角 等分成60份 1′的角
1?的角 等分成60份 1 ?? 的角
1°= ____″
3600
注意:度分秒是60进制的
例1、
把23°36′化成用度表示的角.
解:先把36 ′化成度,即
36 ′=(36÷60)°=0.6 °
所以 23°36′=23.6 °
例题精析
例2、
解:因为1°=60′,所以
0.12°= 60′× 0.12=7.2′
又因为 1′=60? ,
所以 0.2 ′=60? ×0.2=12?
因此 95.12°=95 °7′12?
把95.12°化成用度、分、秒表示的角
例题精析
解:
例3、计算
例题精析
1.用度、分、秒表示:
⑴0.75°= ′= ″
⑵(-)°= ′= ″
⑶16.24°= ° ′ ″
4
15
45
2700
16
960
16
14
24
2.用度表示:
⑴1800″= ′=________°
(2)50°40 ′30 ″= 50°__ ′=______°
30
0.5
40.5
50.675
比一比谁算得快
1、用度、分、秒表示48.32°
2、用度表示30°9'36"
练一练
解:∵0.36°=0.36×60′=19.2′
0.2′=0.2×60″=12″
∴48.32°=48°19′12″
解:∵9′=(9÷60)°=0.15°
36″=(36÷3600)°=0.01°
∴30°9′36″=30°+0.15°+0.01°=30.16°
°
基本步骤 :先把秒化成分,并与原有的分合并,再化成度。
练一练
练一练
思考题
180°–(45°17′+52°57′)
解: 原式
= 180°–97°74′
= 180°–98°14′
= 179°60′–98°14′
= 81°46′
辩一辩
如果两个角的度数一个为18.15?,一个为18?15′,它们一样大吗?
注意:计算时,算式的单位要一致。
1.角的两种定义;
2.角的四种表示方法;
3.角的测量方法;
畅谈所得 感悟提升
本节收获知多少?
简单小小角,一点两条边,
取名要慎重,顶点夹中间.
分秒换算须注意,每逢六十才进一.
画它要牢记,先点再画边.
莫把“∠”相忘
字母数字前,
思考题:1.数一数下面一共有几角?
一共有 6个角
O
A
B
C
D
课后拓展
3条射线
4条射线
5条射线
6条射线
B
F
K
P
3条射线时有___个角;4条射线时有___个角,
5条射线有____个角;6条射线时有___个角;
那么n条射线时有___________个角。
课后拓展
思考题:2.看图填空:
O
O
∠AOB内射线条数
1
2
3
4
…
99
…
n
角的个数
3.根据所给的图形填写下表
静态定义
动态定义
角
定义
表示法
角的测量
与换算
用三个
大写字母
用数字或
希腊字母
用顶点字
母表示
角度制
的换算
角的和
差运算
角的和
差运算
归纳
下课了!
再见!
Thank you!
