苏科版数学八年级上册 5.2 平面直角坐标系 课件(共25张ppt)
文档属性
| 名称 | 苏科版数学八年级上册 5.2 平面直角坐标系 课件(共25张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 549.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 12:50:52 | ||
图片预览




文档简介
平面直角坐标系(1)
无锡市金桥双语实验学校 苏臻
北京东路
北京西路
中山北路
中山南路
图2是某时刻拍摄的某地区的俯视图,此时汽车A、B、C、D、E、F 离站台O的距离分别为200 米、100 米、100 米、200 米、150 米、100 米;音乐喷泉G 距南北路100 米,距东西路150米。
-100
200
100
0
-200
A
B
O
C
D
E
F
150
-100
O
早在1637 年以前, 法国数学家、解析几何的创始人笛卡尔受到了经纬度的启发, 地理上的经纬度是以赤道和本初子午线为标准的, 这两条线从局部上可以看成是平面内互相垂直的两条直线,所以笛卡尔的方法就是在平面内画两条原点重合、互相垂直且具有相同单位长度的数轴建立平面直角坐标系, 从而解决了用一对实数表示平面内的点的位置的问题.
5
-5
-2
-3
-4
-1
3
2
4
1
-6
6
y
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
x
x轴或横轴
y轴或纵轴
原点
平面直角坐标系
第一象限
第二象限
第三象限
第四象限
注意:坐标轴上的点不属于任何象限.
像这样,平面上互相垂直且有
公共原点的两条数轴构成平面
直角坐标系,简称为直角坐标系。
两条数轴:(一般性特征)
(1)互相垂直
(2)原点重合
(3)通常取向上、向右为正方向
(4)单位长度一般要取相同的
请你在给定的网格内建立一个平面直角坐标系,并说一说:在建立平面直角坐标系的时候有哪些需要注意的地方?
北京东路
北京西路
中山北路
中山南路
G
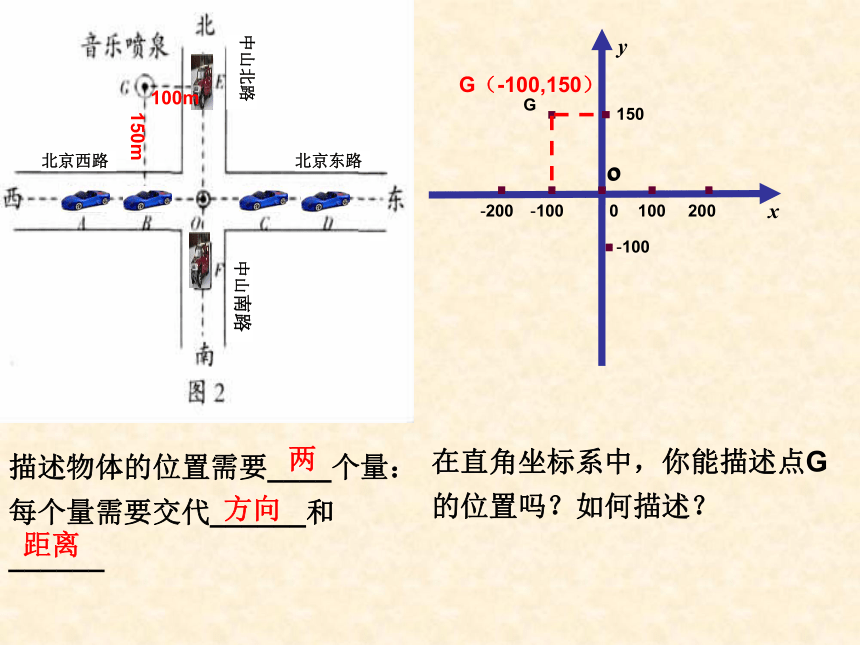
描述物体的位置需要____个量: 每个量需要交代______和______
在直角坐标系中,你能描述点G 的位置吗?如何描述?
O
-100
200
100
0
-200
x
150
-100
O
y
100m
150m
距离
方向
两
G(-100,150)
G(-100,150)
A
B
O
C
D
-100
200
100
0
-200
x
E
F
150
-100
O
y
P(150,-100)
150
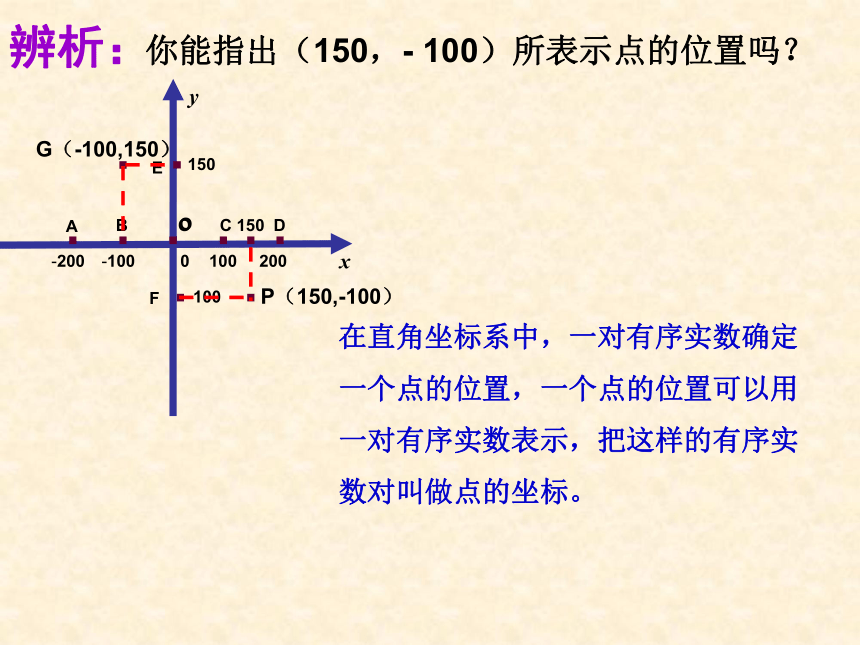
辨析:
你能指出(150,- 100)所表示点的位置吗?
在直角坐标系中,一对有序实数确定
一个点的位置,一个点的位置可以用
一对有序实数表示,把这样的有序实
数对叫做点的坐标。
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
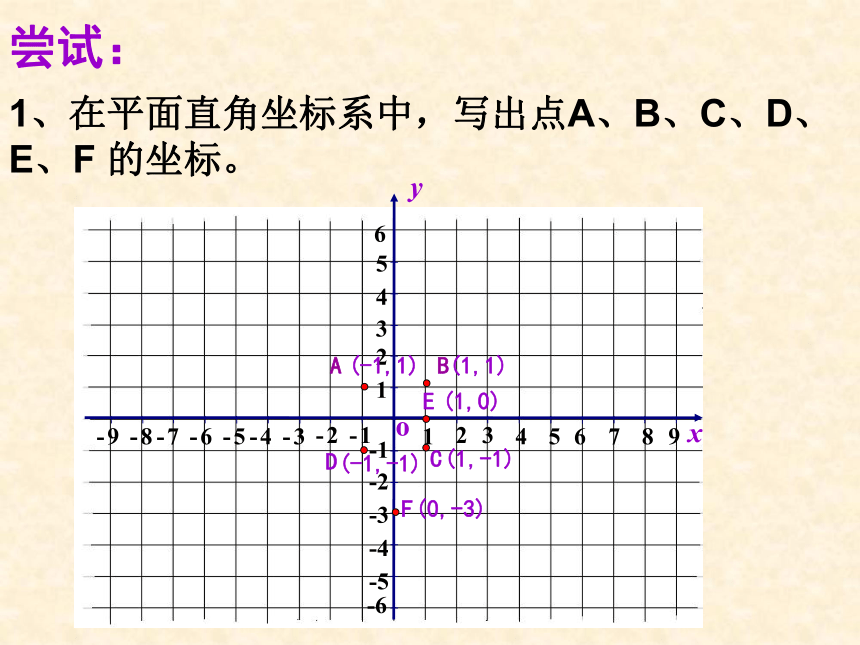
A
B
C
D
E
F
(-1,1)
1、在平面直角坐标系中,写出点A、B、C、D、E、F 的坐标。
-6
6
(1,1)
(1,0)
(1,-1)
(0,-3)
(-1,-1)
尝试:
x
y
o
-1
1
-1
1
a
b
P
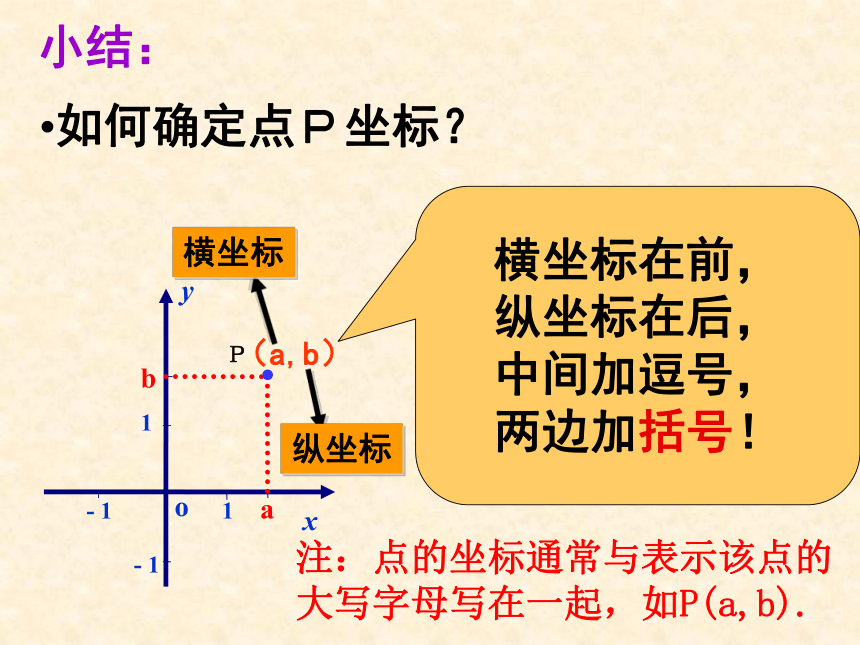
如何确定点P坐标?
(a,b)
横坐标在前,
纵坐标在后,
中间加逗号,
两边加括号!
横坐标
纵坐标
小结:
注:点的坐标通常与表示该点的大写字母写在一起,如P(a,b).
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
2、在平面直角坐标系中,描出坐标(- 3,6)、
(0,6)、(3,6)、(3,3)、(3,- 3)、
(- 3,- 3)、(- 1,0)、(- 3,3) 所对应的点G、H、
I、J、K、L、M、N.
-6
6
G(-3,6)
H(0,6)
I(3,6)
J(3,3)
K(3,-3)
L(-3,-3)
M(-1,0)
N(-3,3)
Q的坐标为(m,n),如何确定Q的位置呢?
y
o
-1
1
-1
1
m
n
Q
x
1、过在x轴上表示m的
点作x轴的垂线
2、过y轴上表示n的点
作y轴的垂线
3、两线的交点即为点Q。
小结:
找出错误的语句,并加以纠正.
①原点的坐标为0;
②直角坐标系中的点都在象限内;
③(2,- 1)与(- 1,2)是同一个点;
④直角坐标系中的点与有序实数对一一对应;
⑤(0,2)在x轴上。
阶段练习1
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
B
C
D
E
(-1,1)
-6
6
(1,1)
(1,-1)
G(-3,6)
(-1,-1)
I(3,6)
J(3,3)
K(3,-3)
L(-3,-3)
N(-3,3)
符号特征:
(-,+)
(+,+)
(-,-)
(+,-)
平面直角坐标系中点的坐标的特征:
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
C
E
F
-6
6
(1,0)
(1,-1)
(0,-3)
G(-3,6)
H(0,6)
I(3,6)
J(3,3)
L(-3,-3)
M(-1,0)
P(x,y) 到x轴的距离为___,y轴的距离为___。
绝对值特征:
坐标轴上点的坐标有何特征?
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
E
F
-6
6
(1,0)
(0,-3)
H(0,6)
M(-1,0)
在x轴上_____________;在y轴上________;
原点________.
纵坐标为0
横坐标为0
(0,0)
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
-6
6
②一般情况下,表示点的坐标的两个数值不能互换,有没有一个点的坐标,它的两个数值可以互换?若有,它在哪里?
1、二四象限角平分线上的点的坐标有什么特征?
2、对于点P(a,b),a的数值变化、b的数值不变,那么点P的位
置会发生怎样的变化?可举例说明。
3、对于点P(a,b),a的数值不变、b的数值变化,那么点P的位
置会发生怎样的变化?可举例说明。
思考:
阶段练习2:
1、横坐标为负,纵坐标为正的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
B
2、已知点P的坐标为(2a-1,a-5)
①若a=3,则P在第______象限;
②若P在第四象限,则a________;
③若P在x轴上,则a________;
④若P在坐标轴上,则a________;
⑤若P在一、三象限角平分线上,则a_______.
四
—
1
2
﹤a﹤5
=5
a=5或
—
1
2
=-4
3、点A在x轴的正半轴上,距离原点4个单位长度,
则A点的坐标是_______.
变1:点A在x轴上,距离原点4个单位长度,则A点的坐标是_______________;
变2:点A到x轴的距离是3,到y轴的距离是9,若
点A在第二象限,则A点的坐标是_______;
变3:点A到x轴的距离是3,到y轴的距离是9,
则A点的坐标是_________________________;
(4,0)
(4,0)
或(-4,0)
(-9,3)
(-9,3)或(9,3)或(9,-3)或
(-9,-3)
4、在直角坐标系中,点A(-3,4),
点B(3,4),线段AB所在的直
线与_____轴平行.
变:在直角坐标系中,点C(-3,-4),点D(-3,4),线段CD所在的直
线与_____轴平行.
x
y
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
B
C
D
E
F
-6
6
G
H
I
J
K
L
M
N
5、颁奖:把图5中的点G、H、I、J、B、
E、C、K、F、L、D、M、A、N、G 顺
次连接,欣赏一下你的杰作。
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
B
C
D
E
F
-6
6
G
H
I
J
K
L
M
N
5、颁奖:把图4 中的点G、H、I、J、B、
E、C、K、F、L、D、M、A、N、G 顺
次连接,欣赏一下你的杰作。
丰收园
本节课你学到了哪些知识?
学会了哪些本领?
掌握了哪些数学思想方法?
还有哪些困惑?
课堂小结:
一种工具——平面直角坐标系
一种方法——确定点及图形的位置
一种思想——数形结合(数缺形时少直观,形缺数时难入微)
一次经历——建立平面直角坐标系及其运用过程
一份收获——多了解决问题的工具,解决问题的思想方法
作业:
1、学案课后练习
2、课后反思
无锡市金桥双语实验学校 苏臻
北京东路
北京西路
中山北路
中山南路
图2是某时刻拍摄的某地区的俯视图,此时汽车A、B、C、D、E、F 离站台O的距离分别为200 米、100 米、100 米、200 米、150 米、100 米;音乐喷泉G 距南北路100 米,距东西路150米。
-100
200
100
0
-200
A
B
O
C
D
E
F
150
-100
O
早在1637 年以前, 法国数学家、解析几何的创始人笛卡尔受到了经纬度的启发, 地理上的经纬度是以赤道和本初子午线为标准的, 这两条线从局部上可以看成是平面内互相垂直的两条直线,所以笛卡尔的方法就是在平面内画两条原点重合、互相垂直且具有相同单位长度的数轴建立平面直角坐标系, 从而解决了用一对实数表示平面内的点的位置的问题.
5
-5
-2
-3
-4
-1
3
2
4
1
-6
6
y
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
x
x轴或横轴
y轴或纵轴
原点
平面直角坐标系
第一象限
第二象限
第三象限
第四象限
注意:坐标轴上的点不属于任何象限.
像这样,平面上互相垂直且有
公共原点的两条数轴构成平面
直角坐标系,简称为直角坐标系。
两条数轴:(一般性特征)
(1)互相垂直
(2)原点重合
(3)通常取向上、向右为正方向
(4)单位长度一般要取相同的
请你在给定的网格内建立一个平面直角坐标系,并说一说:在建立平面直角坐标系的时候有哪些需要注意的地方?
北京东路
北京西路
中山北路
中山南路
G
描述物体的位置需要____个量: 每个量需要交代______和______
在直角坐标系中,你能描述点G 的位置吗?如何描述?
O
-100
200
100
0
-200
x
150
-100
O
y
100m
150m
距离
方向
两
G(-100,150)
G(-100,150)
A
B
O
C
D
-100
200
100
0
-200
x
E
F
150
-100
O
y
P(150,-100)
150
辨析:
你能指出(150,- 100)所表示点的位置吗?
在直角坐标系中,一对有序实数确定
一个点的位置,一个点的位置可以用
一对有序实数表示,把这样的有序实
数对叫做点的坐标。
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
B
C
D
E
F
(-1,1)
1、在平面直角坐标系中,写出点A、B、C、D、E、F 的坐标。
-6
6
(1,1)
(1,0)
(1,-1)
(0,-3)
(-1,-1)
尝试:
x
y
o
-1
1
-1
1
a
b
P
如何确定点P坐标?
(a,b)
横坐标在前,
纵坐标在后,
中间加逗号,
两边加括号!
横坐标
纵坐标
小结:
注:点的坐标通常与表示该点的大写字母写在一起,如P(a,b).
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
2、在平面直角坐标系中,描出坐标(- 3,6)、
(0,6)、(3,6)、(3,3)、(3,- 3)、
(- 3,- 3)、(- 1,0)、(- 3,3) 所对应的点G、H、
I、J、K、L、M、N.
-6
6
G(-3,6)
H(0,6)
I(3,6)
J(3,3)
K(3,-3)
L(-3,-3)
M(-1,0)
N(-3,3)
Q的坐标为(m,n),如何确定Q的位置呢?
y
o
-1
1
-1
1
m
n
Q
x
1、过在x轴上表示m的
点作x轴的垂线
2、过y轴上表示n的点
作y轴的垂线
3、两线的交点即为点Q。
小结:
找出错误的语句,并加以纠正.
①原点的坐标为0;
②直角坐标系中的点都在象限内;
③(2,- 1)与(- 1,2)是同一个点;
④直角坐标系中的点与有序实数对一一对应;
⑤(0,2)在x轴上。
阶段练习1
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
B
C
D
E
(-1,1)
-6
6
(1,1)
(1,-1)
G(-3,6)
(-1,-1)
I(3,6)
J(3,3)
K(3,-3)
L(-3,-3)
N(-3,3)
符号特征:
(-,+)
(+,+)
(-,-)
(+,-)
平面直角坐标系中点的坐标的特征:
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
C
E
F
-6
6
(1,0)
(1,-1)
(0,-3)
G(-3,6)
H(0,6)
I(3,6)
J(3,3)
L(-3,-3)
M(-1,0)
P(x,y) 到x轴的距离为___,y轴的距离为___。
绝对值特征:
坐标轴上点的坐标有何特征?
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
E
F
-6
6
(1,0)
(0,-3)
H(0,6)
M(-1,0)
在x轴上_____________;在y轴上________;
原点________.
纵坐标为0
横坐标为0
(0,0)
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
-6
6
②一般情况下,表示点的坐标的两个数值不能互换,有没有一个点的坐标,它的两个数值可以互换?若有,它在哪里?
1、二四象限角平分线上的点的坐标有什么特征?
2、对于点P(a,b),a的数值变化、b的数值不变,那么点P的位
置会发生怎样的变化?可举例说明。
3、对于点P(a,b),a的数值不变、b的数值变化,那么点P的位
置会发生怎样的变化?可举例说明。
思考:
阶段练习2:
1、横坐标为负,纵坐标为正的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
B
2、已知点P的坐标为(2a-1,a-5)
①若a=3,则P在第______象限;
②若P在第四象限,则a________;
③若P在x轴上,则a________;
④若P在坐标轴上,则a________;
⑤若P在一、三象限角平分线上,则a_______.
四
—
1
2
﹤a﹤5
=5
a=5或
—
1
2
=-4
3、点A在x轴的正半轴上,距离原点4个单位长度,
则A点的坐标是_______.
变1:点A在x轴上,距离原点4个单位长度,则A点的坐标是_______________;
变2:点A到x轴的距离是3,到y轴的距离是9,若
点A在第二象限,则A点的坐标是_______;
变3:点A到x轴的距离是3,到y轴的距离是9,
则A点的坐标是_________________________;
(4,0)
(4,0)
或(-4,0)
(-9,3)
(-9,3)或(9,3)或(9,-3)或
(-9,-3)
4、在直角坐标系中,点A(-3,4),
点B(3,4),线段AB所在的直
线与_____轴平行.
变:在直角坐标系中,点C(-3,-4),点D(-3,4),线段CD所在的直
线与_____轴平行.
x
y
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
B
C
D
E
F
-6
6
G
H
I
J
K
L
M
N
5、颁奖:把图5中的点G、H、I、J、B、
E、C、K、F、L、D、M、A、N、G 顺
次连接,欣赏一下你的杰作。
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
B
C
D
E
F
-6
6
G
H
I
J
K
L
M
N
5、颁奖:把图4 中的点G、H、I、J、B、
E、C、K、F、L、D、M、A、N、G 顺
次连接,欣赏一下你的杰作。
丰收园
本节课你学到了哪些知识?
学会了哪些本领?
掌握了哪些数学思想方法?
还有哪些困惑?
课堂小结:
一种工具——平面直角坐标系
一种方法——确定点及图形的位置
一种思想——数形结合(数缺形时少直观,形缺数时难入微)
一次经历——建立平面直角坐标系及其运用过程
一份收获——多了解决问题的工具,解决问题的思想方法
作业:
1、学案课后练习
2、课后反思
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
