对数函数图像及基本性质
图片预览

文档简介
对数函数
【知识要点】
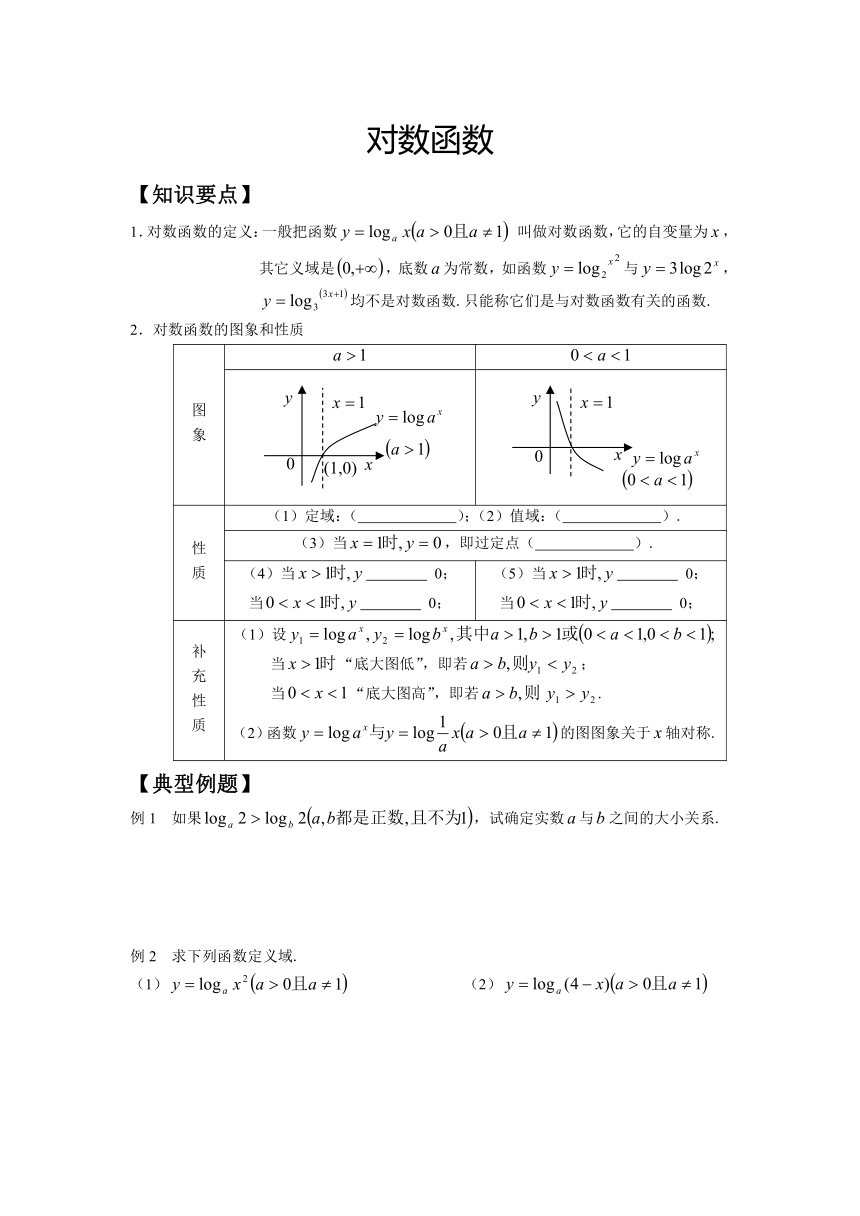
1.对数函数的定义:一般把函数叫做对数函数,它的自变量为,其它义域是,底数为常数,如函数与,均不是对数函数.只能称它们是与对数函数有关的函数.
2.对数函数的图象和性质
图象
性质 (1)定域:( );(2)值域:( ).
(3)当,即过定点( ).
(4)当 0;当 0; (5)当 0;当 0;
补充性质 (1)设当“底大图低”,即若;当“底大图高”,即若.(2)函数的图图象关于轴对称.
【典型例题】
例1 如果,试确定实数与之间的大小关系.
例2 求下列函数定义域.
(1) (2)
(3)
例3 求下列函数定义域
(1) (2)
(3) (4)
(5) (6)
例4 判断函数的单调性.
例5 已知函数
(1)求的定义域
(2)讨论在其定义域内的单调性.
例6 求使为负值的的取值范围.
例7 已知函数是函数图象上的点时,点是函数图象上的点.
(1)写出函数的解析式.
(2)当时,求的取值范围,并求此时函数的最大值.
例8 已知函数的最大值,及取得最大值时的值.
课堂练习及课后小测
1.若函数在区间上的最大值是最小值的3倍,则的值为( ).
A. B. C. D.
2.函数( ).
A. B.
C. D.
3.如果的取值范围是 .
4.若的单调递减区间是 .
5.若.
(1)证明在上是减函数. (2)解不等式.
6.设函数.
(1)求函数的定义域;(2)在函数的图象上是否存在不同的两点,使过这两点的直线平行于轴;(2)当满足什么条件时,在区间上恒取正值.
7.若,求函数的最大值与最小值及相应的的值.
8.已知时,试比较的大小.
(1,0)
【知识要点】
1.对数函数的定义:一般把函数叫做对数函数,它的自变量为,其它义域是,底数为常数,如函数与,均不是对数函数.只能称它们是与对数函数有关的函数.
2.对数函数的图象和性质
图象
性质 (1)定域:( );(2)值域:( ).
(3)当,即过定点( ).
(4)当 0;当 0; (5)当 0;当 0;
补充性质 (1)设当“底大图低”,即若;当“底大图高”,即若.(2)函数的图图象关于轴对称.
【典型例题】
例1 如果,试确定实数与之间的大小关系.
例2 求下列函数定义域.
(1) (2)
(3)
例3 求下列函数定义域
(1) (2)
(3) (4)
(5) (6)
例4 判断函数的单调性.
例5 已知函数
(1)求的定义域
(2)讨论在其定义域内的单调性.
例6 求使为负值的的取值范围.
例7 已知函数是函数图象上的点时,点是函数图象上的点.
(1)写出函数的解析式.
(2)当时,求的取值范围,并求此时函数的最大值.
例8 已知函数的最大值,及取得最大值时的值.
课堂练习及课后小测
1.若函数在区间上的最大值是最小值的3倍,则的值为( ).
A. B. C. D.
2.函数( ).
A. B.
C. D.
3.如果的取值范围是 .
4.若的单调递减区间是 .
5.若.
(1)证明在上是减函数. (2)解不等式.
6.设函数.
(1)求函数的定义域;(2)在函数的图象上是否存在不同的两点,使过这两点的直线平行于轴;(2)当满足什么条件时,在区间上恒取正值.
7.若,求函数的最大值与最小值及相应的的值.
8.已知时,试比较的大小.
(1,0)
