初中数学湘教版九年级下册第一章1.5二次函数的应用练习题(Word版 含解析)
文档属性
| 名称 | 初中数学湘教版九年级下册第一章1.5二次函数的应用练习题(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 83.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 23:17:36 | ||
图片预览



文档简介
初中数学湘教版九年级下册第一章1.5二次函数的应用练习题
一、选择题
设等边三角形的边长为,面积为y,则y与x的函数关系式是
A.
B.
C.
D.
足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度单位:与足球被踢出后经过的时间单位:之间的关系如下表:
?t
?0
?1
?2
?3
?4
?5
?6
?7
?h
?0
?8
?14
?18
?20
?20
?18
?14
下列结论:足球距离地面的最大高度为20m;足球飞行路线的对称轴是直线;足球被踢出9s时落地;足球被踢出时,距离地面的高度是其中正确结论的个数是
A.
1
B.
2
C.
3
D.
4
定点投篮是同学们喜爱的体育项目之一,某位同学投出篮球的飞行路线可以看作是抛物线的一部分,篮球飞行的竖直高度单位:与水平距离单位:近似满足函数关系下表记录了该同学将篮球投出后的x与y的三组数据,根据上述函数模型和数据,可推断出篮球飞行到最高点时,水平距离为
单位:
0
2
4
单位:
A.
B.
2m
C.
D.
3m
飞机着陆后滑行的距离单位:关于滑行时间t以单位:的函数解析式是在飞机着陆滑行中,滑行最后的150m所用的时间是.
A.
10
B.
20
C.
30
D.
10或30
如图,一位运动员推铅球,铅球行进高度与水平距离之间的关系是,则此运动员把铅球推出多远
A.
12m
B.
10m
C.
3m
D.
4m
烟花厂某种礼炮的升空高度与飞行时间的关系式是,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为?
?
A.
4s
B.
5s
C.
6s
D.
10s
生产季节性产品的企业,当它的产品无利润时就会及时停产,现有一生产季节性产品的企业,一年中获得利润y与月份n之间的函数关系式是,那么该企业一年中应停产的月份是
A.
1月,2月
B.
1月,2月,3月
C.
3月,12月
D.
1月,2月,3月,12月
运动会上,某运动员掷铅球时,所掷铅球的高与水平距离之间的函数表达式为,则该运动员的成绩是?
???
A.
B.
C.
D.
一件工艺品的进价为100元,标价135元出售,每天可售出100件.根据销售统计,该件工艺品每降价1元出售,则每天可多售出4件.要使每天获得的利润最大,每件需降价的钱数为
A.
5元
B.
10元
C.
0元
D.
6元
已知学校航模组设计制作的火箭的升空高度与飞行时间满足函数表达式则下列说法中正确的是
A.
点火后9s和点火后13s的升空高度相同
B.
点火后24s火箭落于地面
C.
点火后10s的升空高度为139m
D.
火箭升空的最大高度为145m
二、填空题
汽车刹车后行驶的距离单位:米关于行驶的时间单位:秒的函数解析式是,汽车刹车后停下来前进的距离是______米.
飞机着陆后滑行的距离单位:关于滑行时间单位:的函数解析式是在飞机着陆滑行中,滑行最后的150m所用的时间是______
已知学校航模组设计制作的火箭的升空高度与飞行时间满足函数表达式,则点火后______s时,火箭能达到最大高度.
从地面竖直向上先后抛出两个小球,小球的高度单位:与小球运动时间单位:之间的函数关系式为,若后抛出的小球经过比先抛出的小球高,则抛出两个小球的间隔时间是___________s.
飞机着陆后滑行的距离单位:关于滑行时间单位:的函数解析式是,则经过________s后,飞机停止滑行.
在边长为的正方形铁片中间剪去一个边长是x
cm的小正方形铁片,剩下的四方框铁片的面积与之间的函数关系是_____________.
三、解答题
小李在景区销售一种旅游纪念品,已知每件进价为6元,当销售单价定为8元时,每天可以销售200件.市场调查反映:销售单价每提高1元,日销量将会减少10件,物价部门规定:销售单价不能超过12元,设该纪念品的销售单价为元,日销量为件,日销售利润为元.
求y与x的函数关系式.
要使日销售利润为720元,销售单价应定为多少元?
求日销售利润元与销售单价元的函数关系式,当x为何值时,日销售所获利润最大,并求出此时的利润率.
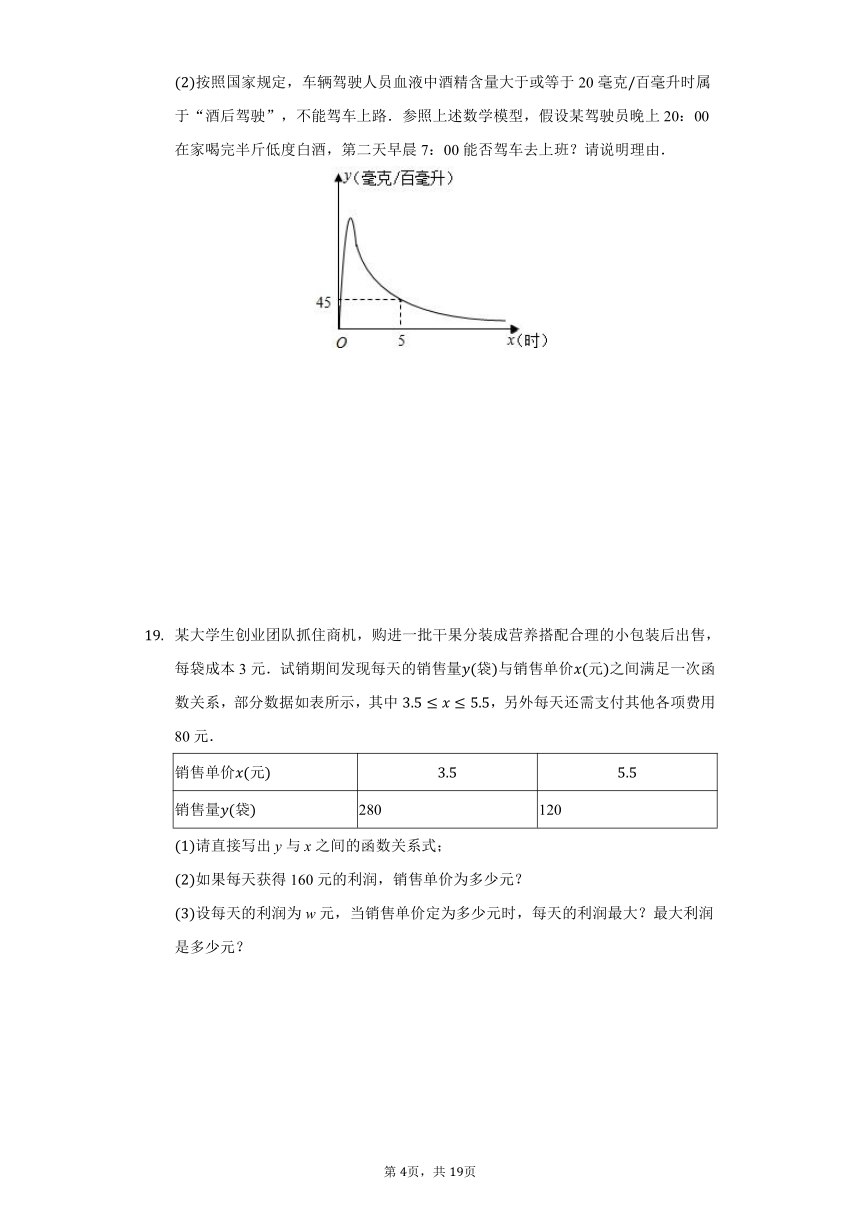
如图,实验数据显示,一般成年人喝半斤低度白酒后,时内其血液中酒精含量毫克百毫升与时间时的关系可以近似的用二次函数刻画,小时后包括小时与x可近似的用反比例函数刻画.
根据上述数学模型计算;
喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
当时,,求k的值.
按照国家规定,车辆驾驶人员血液中酒精含量大于或等于20毫克百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早晨7:00能否驾车去上班?请说明理由.
某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量袋与销售单价元之间满足一次函数关系,部分数据如表所示,其中,另外每天还需支付其他各项费用80元.
销售单价元
销售量袋
280
120
请直接写出y与x之间的函数关系式;
如果每天获得160元的利润,销售单价为多少元?
设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
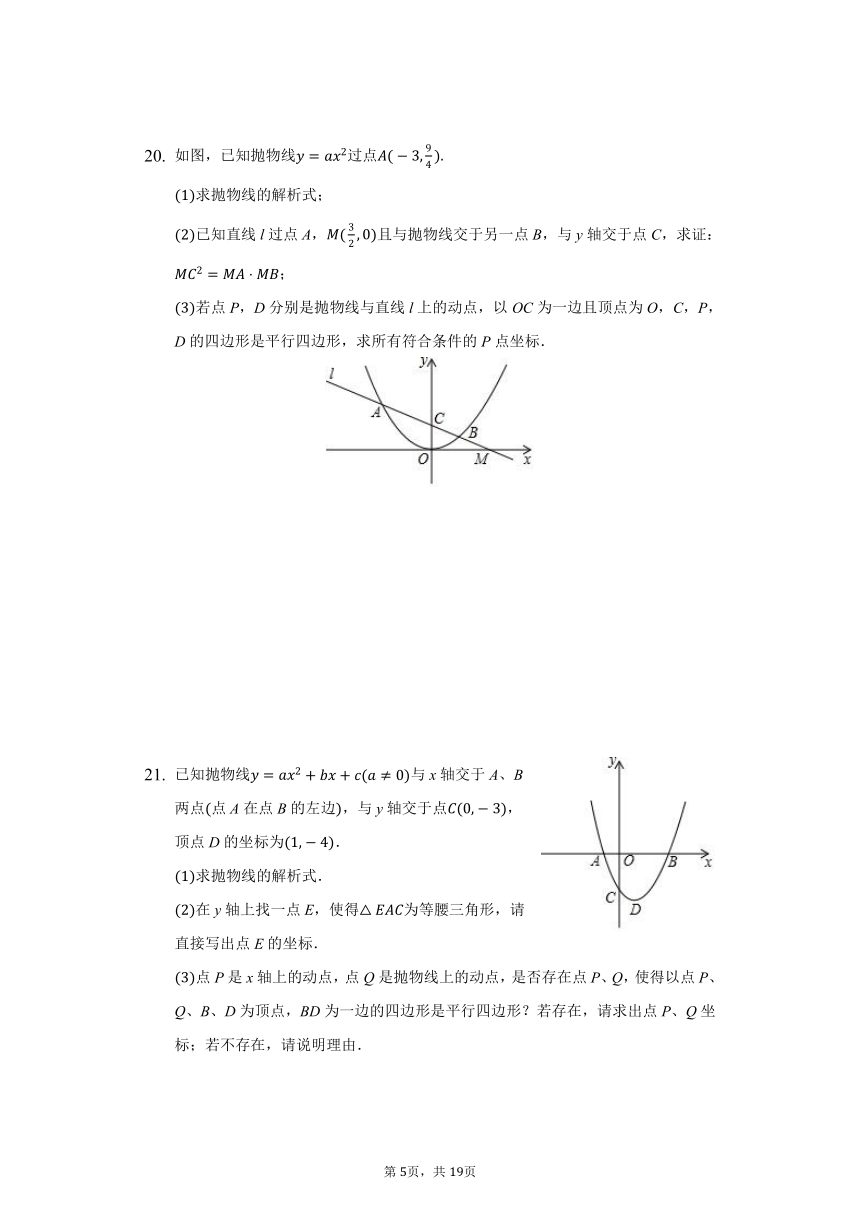
如图,已知抛物线过点
求抛物线的解析式;
已知直线l过点A,且与抛物线交于另一点B,与y轴交于点C,求证:;
若点P,D分别是抛物线与直线l上的动点,以OC为一边且顶点为O,C,P,D的四边形是平行四边形,求所有符合条件的P点坐标.
已知抛物线与x轴交于A、B两点点A在点B的左边,与y轴交于点,顶点D的坐标为.
求抛物线的解析式.
在y轴上找一点E,使得为等腰三角形,请直接写出点E的坐标.
点P是x轴上的动点,点Q是抛物线上的动点,是否存在点P、Q,使得以点P、Q、B、D为顶点,BD为一边的四边形是平行四边形?若存在,请求出点P、Q坐标;若不存在,请说明理由.
答案和解析
1.【答案】D
【解析】解:作出BC边上的高AD.
是等边三角形,边长为x,
,
高为,
.
故选:D.
作出三角形的高,利用直角三角形的性质及勾股定理可得高,利用三角形的面积底高,把相关数值代入即可求解.
此题主要考查了三角形的面积的求法,找到等边三角形一边上的高是难点,求出三角形的高是解决问题的关键.
2.【答案】B
【解析】解:由题意,抛物线的解析式为,把代入可得,
,
足球距离地面的最大高度为,故错误,
抛物线的对称轴,故正确,
时,,
足球被踢出9s时落地,故正确,
时,,故错误.
正确的有,
故选:B.
由题意,抛物线经过,,所以可以假设抛物线的解析式为,把代入可得,可得,由此即可一一判断.
本题考查二次函数的应用、求出抛物线的解析式是解题的关键,属于中考常考题型.
3.【答案】C
【解析】解:设二次函数的解析式为,
根据表可得:,
解得:,
,
可推断出篮球飞行到最高点时,水平距离为米,
故选:C.
首先根据提供数据列出函数解析式,然后确定其顶点坐标的横坐标即为本题答案.
考查了二次函数的应用,解题的关键是正确的求得解析式,难度不大.
4.【答案】A
【解析】解:当y取得最大值时,飞机停下来,
则,
此时,飞机着陆后滑行600米才能停下来.
因此t的取值范围是;
即当时,
即,
解得:,不合题意舍去,
滑行最后的150m所用的时间是,
故选:A.
由于飞机着陆,不会倒着跑,所以当y取得最大值时,t也取得最大值,求得t的取值范围,然后解方程即可得到结论.
本题考查二次函数和一元二次方程的应用,解题的关键是明确题意,找出所求问题需要的条件.
5.【答案】B
【解析】解:令
则:
舍,
由题意可知当时,符合题意
故选:B.
令,解得符合题意的x值,则该值为此运动员把铅球推出的距离,据此可解.
本题考查了二次函数在实际问题中的应用,能根据题意正确列式并求解,是解题的关键.
6.【答案】B
【解析】
【分析】
本题考查了二次函数的应用,解题的关键是将二次函数的关系式变形为顶点式.本题属于基础题,难度不大,解决该题型题目时,将函数的关系式进行变换找出顶点坐标即可.将h关于t的函数关系式变形为顶点式,即可得出升到最高点的时间,从而得出结论.
【解答】
解:,
当时,礼炮升到最高点.
故选B.
7.【答案】D
【解析】
【分析】
本题考查了二次函数的应用:根据二次函数的性质解决实际问题.求出利润为0时n的值,即令,则,解方程得到,,所以3月和12月要停产,然后根据二次函数的性质得到抛物线开口向下,则和时,,于是得到该企业一年中应停产的月份还有1月,2月.
【解答】
解:令,则,
,
,
,,
,
抛物线开口向下,
和时,,
该企业一年中应停产的月份是1月,2月,3月,12月.
故选D.
8.【答案】D
【解析】
【分析】
本题考查二次函数的实际应用,搞清楚铅球落地时,即,测量运动员成绩,也就是求x的值,此题为数学建模题,借助二次函数解决实际问题.
铅球落地才能计算成绩,此时,即,解方程即可.在实际问题中,注意负值舍去.
【解答】
解:由题意可知,把代入解析式得:,
解方程得,舍去,
即该运动员的成绩是10米.
故选D.
9.【答案】A
【解析】
【分析】
本题考查了二次函数的应用.
设每件降价x元,每天获得的利润为W元,根据总利润每件的利润总销量列出关系式,根据二次函数的性质即可得到答案.
【解答】
解:设每件降价x元,每天获得的利润为W元,
根据题意得:,
,降价5元时,每天获得的利润最大,最大利润为3600元.
故选A.
10.【答案】D
【解析】解:A、当时,;当时,;所以点火后9s和点火后13s的升空高度不相同,此选项错误;
B、当时,,所以点火后24s火箭离地面的高度为1m,此选项错误;
C、当时,,此选项错误;
D、由知火箭升空的最大高度为145m,此选项正确.
故选:D.
分别求出、13、24、10时h的值可判断A、B、C三个选项,将解析式配方成顶点式可判断D选项.
本题主要考查二次函数的应用,解题的关键是熟练掌握二次函数的性质.
11.【答案】8
【解析】解:
,
故当时,s最大为8m.
故答案为:8.
直接利用配方法求出二次函数最值进而得出答案.
此题主要考查了二次函数的应用,正确应用配方法是解题关键.
12.【答案】10
【解析】解:当y取得最大值时,飞机停下来,
则,
此时,飞机着陆后滑行600米才能停下来.
因此t的取值范围是;
即当时,
即,
解得:,不合题意舍去,
滑行最后的150m所用的时间是,
故答案是:10.
由于飞机着陆,不会倒着跑,所以当y取得最大值时,t也取得最大值,求得t的取值范围,然后解方程即可得到结论.
本题考查二次函数的应用,解题的关键是明确题意,找出所求问题需要的条件.
13.【答案】12
【解析】解:
二次项系数为,
抛物线开口向下,当时,h取得最大值,即点火12s时,火箭能达到最大高度.
故答案为:12.
将函数解析式配方,写成顶点式,按照二次函数的性质可得答案.
本题考查了二次函数的应用,熟练掌握配方法及二次函数的性质,是解题的关键.
14.【答案】
【解析】
【分析】
此题主要考查了二次函数的应用,正确理解题意是解题关键.
把代入,求得,当时,解方程即可得到结论.
【解答】
解:把代入,得,,
当时,即,
解得:或不合题意舍去,
抛出两个小球的间隔时间是,
故答案为.
15.【答案】25
【解析】
【分析】
本题主要考查了二次函数的实际应用.
根据飞机从滑行到停止的路程就是滑行的最大路程,最大值也即飞机停下的距离,求出y的最大值对应的t值即可.
【解答】
解:?,
当时,米,
即飞机着路后滑行25秒后,飞机停止滑行.
故答案为25.
16.【答案】
【解析】
【分析】
此题考查了由实际问题抽象出二次函数,根据题意,找到所求量的等量关系是解决问题的关键.
剩下的四方框铁片的面积边长20cm的正方形铁片面积边长xcm的小正方形铁片面积,即可求得.
【解答】
解:由题意得:
,
故答案为.
17.【答案】解:根据题意得,
,
故y与x的函数关系式为;
根据题意得,
,
解得;,不合题意舍去.
答:要使日销售利润为720元,销售单价应定为10元;
根据题意得,
,
,
当时,w随x的增大而增大,
当时,w所获利润最大,为960元,
答:当x为12时,日销售利润最大,最大利润960元,利润率为.
【解析】根据“销售单价每提高1元日销量将会减少10件”可写出函数表达式,化简即可;
利润单价定价日销售量,通过这个公式可得出日销售利润的函数表达式,将代入表达式,即可求出销售单价的值;
根据第二问即可写出日销售利润元与销售单价元的函数关系式,根据二次函数的性质,即可得出答案.
本题主要考查了二次函数在销售问题中的应用,理清题中的数量关系并明确二次函数的性质是解题的关键.
18.【答案】解:,
当时,y取得最大值,此时,
答:喝酒后1时血液中的酒精含量达到最大值,最大值为200毫克百毫升;
当时,,
,得,
即k的值是225;
该驾驶员第二天早晨7:00不能驾车去上班,
理由:由知,
,
晚上20:00到第二天早晨7:00是11个小时,
将代入,得,
,
该驾驶员第二天早晨7:00不能驾车去上班.
【解析】将二次函数解析式化为顶点式即可解答本题;
根据当时,,代入反比例函数解析式即可求得k的值;
根据题意可以求得晚上20:00到第二天早晨7:00是多少小时,然后代入反比例函数解析式,求出相应的y的值,然后与20比较大小即可解答本题.
本题考查反比例函数的应用、二次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用反比例函数和二次函数的性质解答.
19.【答案】解:设,
将,;,代入,
得,解得,
则y与x之间的函数关系式为;
由题意,得,
整理,得,
解得,.
,
.
答:如果每天获得160元的利润,销售单价为4元;
由题意得:
,
,
当时,w有最大值为240.
故当销售单价定为5元时,每天的利润最大,最大利润是240元.
【解析】根据每天的销售量袋与销售单价元之间满足一次函数关系,可设,再将,;,代入,利用待定系数法即可求解;
根据每天获得160元的利润列出方程,解方程并结合即可求解;
根据每天的利润每天每袋的利润销售量每天还需支付的其他费用,列出w关于x的函数解析式,再根据二次函数的性质即可求解.
本题考查了二次函数的应用,一元二次方程的应用,待定系数法求一次函数的解析式,根据题意找出等量关系列出关系式是解题的关键.
20.【答案】解:把点代入,
得到,
,
抛物线的解析式为.
设直线l的解析式为,则有,
解得,
直线l的解析式为,
令,得到,
,
由,解得或,
,
如图1中,过点A作轴于,过B作轴于,则,
,,
,
即.
如图2中,设
为一边且顶点为O,C,P,D的四边形是平行四边形,
,,
,
,
整理得:或,
解得或或或舍弃,
或或.
【解析】利用待定系数法即可解决问题.
构建方程组确定点B的坐标,再利用平行线分线段成比例定理解决问题即可.
如图2中,设,根据构建方程求出t即可解决问题.
本题属于二次函数综合题,考查了待定系数法,平行四边形的判定和性质等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.
21.【答案】解:抛物线的顶点为,
设抛物线的解析式为,
将点代入抛物线中,得,
,
抛物线的解析式为;
由知,抛物线的解析式为,
令,则,
或,
,,
令,则,
,
,
设点,则,,
是等腰三角形,
当时,,
或点C的纵坐标,舍去,
,
当时,,
,
或,
当时,,
,
,
即满足条件的点E的坐标为、、、;
如图,存在,,
将线段BD向上平移4个单位,再向右或向左平移适当的距离,使点B的对应点落在抛物线上,这样便存在点Q,此时点D的对应点就是点P,
点Q的纵坐标为4,
设,
将点Q的坐标代入抛物线中得,,
或,
或,
分别过点D,Q作x轴的垂线,垂足分别为F,G,
抛物线与x轴的右边的交点B的坐标为,且,
,
点P的横坐标为或,
即、或、.
【解析】根据抛物线的顶点坐标设出抛物线的解析式,再将点C坐标代入求解,即可得出结论;
先求出点A,C坐标,设出点E坐标,表示出AE,CE,AC,再分三种情况建立方程求解即可;
利用平移先确定出点Q的纵坐标,代入抛物线解析式求出点Q的横坐标,即可得出结论.
此题是二次函数综合题,主要考查了待定系数法,等腰三角形的性质,平移的性质,用方程的思想解决问题是解本题的关键.
第2页,共2页
第1页,共1页
一、选择题
设等边三角形的边长为,面积为y,则y与x的函数关系式是
A.
B.
C.
D.
足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度单位:与足球被踢出后经过的时间单位:之间的关系如下表:
?t
?0
?1
?2
?3
?4
?5
?6
?7
?h
?0
?8
?14
?18
?20
?20
?18
?14
下列结论:足球距离地面的最大高度为20m;足球飞行路线的对称轴是直线;足球被踢出9s时落地;足球被踢出时,距离地面的高度是其中正确结论的个数是
A.
1
B.
2
C.
3
D.
4
定点投篮是同学们喜爱的体育项目之一,某位同学投出篮球的飞行路线可以看作是抛物线的一部分,篮球飞行的竖直高度单位:与水平距离单位:近似满足函数关系下表记录了该同学将篮球投出后的x与y的三组数据,根据上述函数模型和数据,可推断出篮球飞行到最高点时,水平距离为
单位:
0
2
4
单位:
A.
B.
2m
C.
D.
3m
飞机着陆后滑行的距离单位:关于滑行时间t以单位:的函数解析式是在飞机着陆滑行中,滑行最后的150m所用的时间是.
A.
10
B.
20
C.
30
D.
10或30
如图,一位运动员推铅球,铅球行进高度与水平距离之间的关系是,则此运动员把铅球推出多远
A.
12m
B.
10m
C.
3m
D.
4m
烟花厂某种礼炮的升空高度与飞行时间的关系式是,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为?
?
A.
4s
B.
5s
C.
6s
D.
10s
生产季节性产品的企业,当它的产品无利润时就会及时停产,现有一生产季节性产品的企业,一年中获得利润y与月份n之间的函数关系式是,那么该企业一年中应停产的月份是
A.
1月,2月
B.
1月,2月,3月
C.
3月,12月
D.
1月,2月,3月,12月
运动会上,某运动员掷铅球时,所掷铅球的高与水平距离之间的函数表达式为,则该运动员的成绩是?
???
A.
B.
C.
D.
一件工艺品的进价为100元,标价135元出售,每天可售出100件.根据销售统计,该件工艺品每降价1元出售,则每天可多售出4件.要使每天获得的利润最大,每件需降价的钱数为
A.
5元
B.
10元
C.
0元
D.
6元
已知学校航模组设计制作的火箭的升空高度与飞行时间满足函数表达式则下列说法中正确的是
A.
点火后9s和点火后13s的升空高度相同
B.
点火后24s火箭落于地面
C.
点火后10s的升空高度为139m
D.
火箭升空的最大高度为145m
二、填空题
汽车刹车后行驶的距离单位:米关于行驶的时间单位:秒的函数解析式是,汽车刹车后停下来前进的距离是______米.
飞机着陆后滑行的距离单位:关于滑行时间单位:的函数解析式是在飞机着陆滑行中,滑行最后的150m所用的时间是______
已知学校航模组设计制作的火箭的升空高度与飞行时间满足函数表达式,则点火后______s时,火箭能达到最大高度.
从地面竖直向上先后抛出两个小球,小球的高度单位:与小球运动时间单位:之间的函数关系式为,若后抛出的小球经过比先抛出的小球高,则抛出两个小球的间隔时间是___________s.
飞机着陆后滑行的距离单位:关于滑行时间单位:的函数解析式是,则经过________s后,飞机停止滑行.
在边长为的正方形铁片中间剪去一个边长是x
cm的小正方形铁片,剩下的四方框铁片的面积与之间的函数关系是_____________.
三、解答题
小李在景区销售一种旅游纪念品,已知每件进价为6元,当销售单价定为8元时,每天可以销售200件.市场调查反映:销售单价每提高1元,日销量将会减少10件,物价部门规定:销售单价不能超过12元,设该纪念品的销售单价为元,日销量为件,日销售利润为元.
求y与x的函数关系式.
要使日销售利润为720元,销售单价应定为多少元?
求日销售利润元与销售单价元的函数关系式,当x为何值时,日销售所获利润最大,并求出此时的利润率.
如图,实验数据显示,一般成年人喝半斤低度白酒后,时内其血液中酒精含量毫克百毫升与时间时的关系可以近似的用二次函数刻画,小时后包括小时与x可近似的用反比例函数刻画.
根据上述数学模型计算;
喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
当时,,求k的值.
按照国家规定,车辆驾驶人员血液中酒精含量大于或等于20毫克百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早晨7:00能否驾车去上班?请说明理由.
某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量袋与销售单价元之间满足一次函数关系,部分数据如表所示,其中,另外每天还需支付其他各项费用80元.
销售单价元
销售量袋
280
120
请直接写出y与x之间的函数关系式;
如果每天获得160元的利润,销售单价为多少元?
设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
如图,已知抛物线过点
求抛物线的解析式;
已知直线l过点A,且与抛物线交于另一点B,与y轴交于点C,求证:;
若点P,D分别是抛物线与直线l上的动点,以OC为一边且顶点为O,C,P,D的四边形是平行四边形,求所有符合条件的P点坐标.
已知抛物线与x轴交于A、B两点点A在点B的左边,与y轴交于点,顶点D的坐标为.
求抛物线的解析式.
在y轴上找一点E,使得为等腰三角形,请直接写出点E的坐标.
点P是x轴上的动点,点Q是抛物线上的动点,是否存在点P、Q,使得以点P、Q、B、D为顶点,BD为一边的四边形是平行四边形?若存在,请求出点P、Q坐标;若不存在,请说明理由.
答案和解析
1.【答案】D
【解析】解:作出BC边上的高AD.
是等边三角形,边长为x,
,
高为,
.
故选:D.
作出三角形的高,利用直角三角形的性质及勾股定理可得高,利用三角形的面积底高,把相关数值代入即可求解.
此题主要考查了三角形的面积的求法,找到等边三角形一边上的高是难点,求出三角形的高是解决问题的关键.
2.【答案】B
【解析】解:由题意,抛物线的解析式为,把代入可得,
,
足球距离地面的最大高度为,故错误,
抛物线的对称轴,故正确,
时,,
足球被踢出9s时落地,故正确,
时,,故错误.
正确的有,
故选:B.
由题意,抛物线经过,,所以可以假设抛物线的解析式为,把代入可得,可得,由此即可一一判断.
本题考查二次函数的应用、求出抛物线的解析式是解题的关键,属于中考常考题型.
3.【答案】C
【解析】解:设二次函数的解析式为,
根据表可得:,
解得:,
,
可推断出篮球飞行到最高点时,水平距离为米,
故选:C.
首先根据提供数据列出函数解析式,然后确定其顶点坐标的横坐标即为本题答案.
考查了二次函数的应用,解题的关键是正确的求得解析式,难度不大.
4.【答案】A
【解析】解:当y取得最大值时,飞机停下来,
则,
此时,飞机着陆后滑行600米才能停下来.
因此t的取值范围是;
即当时,
即,
解得:,不合题意舍去,
滑行最后的150m所用的时间是,
故选:A.
由于飞机着陆,不会倒着跑,所以当y取得最大值时,t也取得最大值,求得t的取值范围,然后解方程即可得到结论.
本题考查二次函数和一元二次方程的应用,解题的关键是明确题意,找出所求问题需要的条件.
5.【答案】B
【解析】解:令
则:
舍,
由题意可知当时,符合题意
故选:B.
令,解得符合题意的x值,则该值为此运动员把铅球推出的距离,据此可解.
本题考查了二次函数在实际问题中的应用,能根据题意正确列式并求解,是解题的关键.
6.【答案】B
【解析】
【分析】
本题考查了二次函数的应用,解题的关键是将二次函数的关系式变形为顶点式.本题属于基础题,难度不大,解决该题型题目时,将函数的关系式进行变换找出顶点坐标即可.将h关于t的函数关系式变形为顶点式,即可得出升到最高点的时间,从而得出结论.
【解答】
解:,
当时,礼炮升到最高点.
故选B.
7.【答案】D
【解析】
【分析】
本题考查了二次函数的应用:根据二次函数的性质解决实际问题.求出利润为0时n的值,即令,则,解方程得到,,所以3月和12月要停产,然后根据二次函数的性质得到抛物线开口向下,则和时,,于是得到该企业一年中应停产的月份还有1月,2月.
【解答】
解:令,则,
,
,
,,
,
抛物线开口向下,
和时,,
该企业一年中应停产的月份是1月,2月,3月,12月.
故选D.
8.【答案】D
【解析】
【分析】
本题考查二次函数的实际应用,搞清楚铅球落地时,即,测量运动员成绩,也就是求x的值,此题为数学建模题,借助二次函数解决实际问题.
铅球落地才能计算成绩,此时,即,解方程即可.在实际问题中,注意负值舍去.
【解答】
解:由题意可知,把代入解析式得:,
解方程得,舍去,
即该运动员的成绩是10米.
故选D.
9.【答案】A
【解析】
【分析】
本题考查了二次函数的应用.
设每件降价x元,每天获得的利润为W元,根据总利润每件的利润总销量列出关系式,根据二次函数的性质即可得到答案.
【解答】
解:设每件降价x元,每天获得的利润为W元,
根据题意得:,
,降价5元时,每天获得的利润最大,最大利润为3600元.
故选A.
10.【答案】D
【解析】解:A、当时,;当时,;所以点火后9s和点火后13s的升空高度不相同,此选项错误;
B、当时,,所以点火后24s火箭离地面的高度为1m,此选项错误;
C、当时,,此选项错误;
D、由知火箭升空的最大高度为145m,此选项正确.
故选:D.
分别求出、13、24、10时h的值可判断A、B、C三个选项,将解析式配方成顶点式可判断D选项.
本题主要考查二次函数的应用,解题的关键是熟练掌握二次函数的性质.
11.【答案】8
【解析】解:
,
故当时,s最大为8m.
故答案为:8.
直接利用配方法求出二次函数最值进而得出答案.
此题主要考查了二次函数的应用,正确应用配方法是解题关键.
12.【答案】10
【解析】解:当y取得最大值时,飞机停下来,
则,
此时,飞机着陆后滑行600米才能停下来.
因此t的取值范围是;
即当时,
即,
解得:,不合题意舍去,
滑行最后的150m所用的时间是,
故答案是:10.
由于飞机着陆,不会倒着跑,所以当y取得最大值时,t也取得最大值,求得t的取值范围,然后解方程即可得到结论.
本题考查二次函数的应用,解题的关键是明确题意,找出所求问题需要的条件.
13.【答案】12
【解析】解:
二次项系数为,
抛物线开口向下,当时,h取得最大值,即点火12s时,火箭能达到最大高度.
故答案为:12.
将函数解析式配方,写成顶点式,按照二次函数的性质可得答案.
本题考查了二次函数的应用,熟练掌握配方法及二次函数的性质,是解题的关键.
14.【答案】
【解析】
【分析】
此题主要考查了二次函数的应用,正确理解题意是解题关键.
把代入,求得,当时,解方程即可得到结论.
【解答】
解:把代入,得,,
当时,即,
解得:或不合题意舍去,
抛出两个小球的间隔时间是,
故答案为.
15.【答案】25
【解析】
【分析】
本题主要考查了二次函数的实际应用.
根据飞机从滑行到停止的路程就是滑行的最大路程,最大值也即飞机停下的距离,求出y的最大值对应的t值即可.
【解答】
解:?,
当时,米,
即飞机着路后滑行25秒后,飞机停止滑行.
故答案为25.
16.【答案】
【解析】
【分析】
此题考查了由实际问题抽象出二次函数,根据题意,找到所求量的等量关系是解决问题的关键.
剩下的四方框铁片的面积边长20cm的正方形铁片面积边长xcm的小正方形铁片面积,即可求得.
【解答】
解:由题意得:
,
故答案为.
17.【答案】解:根据题意得,
,
故y与x的函数关系式为;
根据题意得,
,
解得;,不合题意舍去.
答:要使日销售利润为720元,销售单价应定为10元;
根据题意得,
,
,
当时,w随x的增大而增大,
当时,w所获利润最大,为960元,
答:当x为12时,日销售利润最大,最大利润960元,利润率为.
【解析】根据“销售单价每提高1元日销量将会减少10件”可写出函数表达式,化简即可;
利润单价定价日销售量,通过这个公式可得出日销售利润的函数表达式,将代入表达式,即可求出销售单价的值;
根据第二问即可写出日销售利润元与销售单价元的函数关系式,根据二次函数的性质,即可得出答案.
本题主要考查了二次函数在销售问题中的应用,理清题中的数量关系并明确二次函数的性质是解题的关键.
18.【答案】解:,
当时,y取得最大值,此时,
答:喝酒后1时血液中的酒精含量达到最大值,最大值为200毫克百毫升;
当时,,
,得,
即k的值是225;
该驾驶员第二天早晨7:00不能驾车去上班,
理由:由知,
,
晚上20:00到第二天早晨7:00是11个小时,
将代入,得,
,
该驾驶员第二天早晨7:00不能驾车去上班.
【解析】将二次函数解析式化为顶点式即可解答本题;
根据当时,,代入反比例函数解析式即可求得k的值;
根据题意可以求得晚上20:00到第二天早晨7:00是多少小时,然后代入反比例函数解析式,求出相应的y的值,然后与20比较大小即可解答本题.
本题考查反比例函数的应用、二次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用反比例函数和二次函数的性质解答.
19.【答案】解:设,
将,;,代入,
得,解得,
则y与x之间的函数关系式为;
由题意,得,
整理,得,
解得,.
,
.
答:如果每天获得160元的利润,销售单价为4元;
由题意得:
,
,
当时,w有最大值为240.
故当销售单价定为5元时,每天的利润最大,最大利润是240元.
【解析】根据每天的销售量袋与销售单价元之间满足一次函数关系,可设,再将,;,代入,利用待定系数法即可求解;
根据每天获得160元的利润列出方程,解方程并结合即可求解;
根据每天的利润每天每袋的利润销售量每天还需支付的其他费用,列出w关于x的函数解析式,再根据二次函数的性质即可求解.
本题考查了二次函数的应用,一元二次方程的应用,待定系数法求一次函数的解析式,根据题意找出等量关系列出关系式是解题的关键.
20.【答案】解:把点代入,
得到,
,
抛物线的解析式为.
设直线l的解析式为,则有,
解得,
直线l的解析式为,
令,得到,
,
由,解得或,
,
如图1中,过点A作轴于,过B作轴于,则,
,,
,
即.
如图2中,设
为一边且顶点为O,C,P,D的四边形是平行四边形,
,,
,
,
整理得:或,
解得或或或舍弃,
或或.
【解析】利用待定系数法即可解决问题.
构建方程组确定点B的坐标,再利用平行线分线段成比例定理解决问题即可.
如图2中,设,根据构建方程求出t即可解决问题.
本题属于二次函数综合题,考查了待定系数法,平行四边形的判定和性质等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.
21.【答案】解:抛物线的顶点为,
设抛物线的解析式为,
将点代入抛物线中,得,
,
抛物线的解析式为;
由知,抛物线的解析式为,
令,则,
或,
,,
令,则,
,
,
设点,则,,
是等腰三角形,
当时,,
或点C的纵坐标,舍去,
,
当时,,
,
或,
当时,,
,
,
即满足条件的点E的坐标为、、、;
如图,存在,,
将线段BD向上平移4个单位,再向右或向左平移适当的距离,使点B的对应点落在抛物线上,这样便存在点Q,此时点D的对应点就是点P,
点Q的纵坐标为4,
设,
将点Q的坐标代入抛物线中得,,
或,
或,
分别过点D,Q作x轴的垂线,垂足分别为F,G,
抛物线与x轴的右边的交点B的坐标为,且,
,
点P的横坐标为或,
即、或、.
【解析】根据抛物线的顶点坐标设出抛物线的解析式,再将点C坐标代入求解,即可得出结论;
先求出点A,C坐标,设出点E坐标,表示出AE,CE,AC,再分三种情况建立方程求解即可;
利用平移先确定出点Q的纵坐标,代入抛物线解析式求出点Q的横坐标,即可得出结论.
此题是二次函数综合题,主要考查了待定系数法,等腰三角形的性质,平移的性质,用方程的思想解决问题是解本题的关键.
第2页,共2页
第1页,共1页
