2020-2021学年湘教新版八年级上册数学期末复习试卷1 (word版 含解析)
文档属性
| 名称 | 2020-2021学年湘教新版八年级上册数学期末复习试卷1 (word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 250.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览




文档简介
2020-2021学年湘教新版八年级上册数学期末复习试卷1
一.选择题(共12小题,满分48分,每小题4分)
1.计算的结果为( )
A.
B.
C.
D.
2.能使分式的值为零的所有x的值是( )
A.x=1
B.x=﹣1
C.x=1或x=﹣1
D.x=2或x=1
3.下列命题中,为假命题的是( )
A.等腰三角形是轴对称图形
B.三角形的外角大于它的每一个内角
C.三角形的中线是一条线段
D.两边及其夹角分别相等的两三角形全等
4.如图,AB=DB,∠1=∠2,请问添加下面哪个条件不能判断△ABC≌△DBE的是( )
A.BC=BE
B.AC=DE
C.∠A=∠D
D.∠ACB=∠DEB
5.下列各数中,有理数是( )
A.
B.
C.
D.
6.设的小数部分为b,那么(4+b)b的值是( )
A.1
B.是一个有理数
C.3
D.无法确定
7.实数a,b在数轴上的对应点的位置如图所示,把a,b,0按照从小到大的顺序排列,正确的是( )
A.a<0<b
B.0<a<b
C.b<0<a
D.0<b<a
8.不等式3x+10≤1的解集在数轴上表示正确的是( )
A.
B.
C.
D.
9.不等式组的整数解的个数是( )
A.2
B.3
C.4
D.5
10.在四川抗震救灾中,某抢险地段需实行爆破.操作人员点燃导火线后,要在炸药爆炸前跑到400米以外的安全区域.已知导火线的燃烧速度是1.2厘米/秒,操作人员跑步的速度是5米/秒.为了保证操作人员的安全,导火线的长度要超过( )
A.66厘米
B.76厘米
C.86厘米
D.96厘米
11.若=x﹣5,则x的取值范围是( )
A.x<5
B.x≤5
C.x≥5
D.x>5
12.已知,x+y=﹣5,xy=3,则的结果是( )
A.
B.﹣
C.
D.﹣
二.填空题(共8小题,满分32分,每小题4分)
13.计算:
?=
.
14.把命题“相等的角是对顶角”改写成“如果…,那么…”的形式是
.
15.如图,D,E分别是△ABC的边AB,AC的中点,若△ADE的面积为1,则△ABC的面积等于
.
16.计算﹣等于
.
17.三角形两边长分别是2,4,第三边长为偶数,第三边长为
.
18.当x=
时,的值最小.
19.若a=﹣0.32,b=﹣3﹣2,c=(﹣)﹣2,d=(﹣)0,请用“<”将a、b、c、d连起来:
.
20.如果某不等式组的解集是﹣2≤x<1,那么该不等式组的整数解是
.
三.解答题(共7小题,满分70分)
21.计算:.
22.先化简,再求值:(x﹣2+)÷,其中x=﹣.
23.一节数学课上,老师布置了一道课堂练习:“如图,在△ABC中,∠B=∠C,求证:AB=AC“,小明发现,他取BC的中点D,连接AD后,无法证明△ABD≌△ACD,故举手提问老师,老师听了他的困惑,告诉他只要再作两条垂线段就可以证明了,你知道如何继续证明吗?请你写下完整的证明过程.
24.若:,则:(x?y)1999等于多少.
25.为提高饮水质量,越来越多的居民选购家用净水器.一商场抓住商机,从厂家购进了A、B两种型号家用净水器160台,A型号家用净水器进价是1500元/台,售价是2100元/台,B型号家用净水器进价是3500元/台,售价是4300元/台.为保证售完这160台家用净水器的毛利润不低于116000元,求A型号家用净水器最多能购进多少台?(注:毛利润=售价﹣进价)
26.小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
营业员A:月销售件数200件,月总收入2400元;
营业员B:月销售件数300件,月总收入2700元;
假设营业员的月基本工资为x元,销售每件服装奖励y元.
(1)求x、y的值;
(2)若某营业员的月总收入不低于3100元,那么他当月至少要卖服装多少件?
(3)商场为了多销售服装,对顾客推荐一种购买方式:如果购买甲3件,乙2件,丙1件共需350元;如果购买甲1件,乙2件,丙3件共需370元.某顾客想购买甲、乙、丙各一件共需多少元?
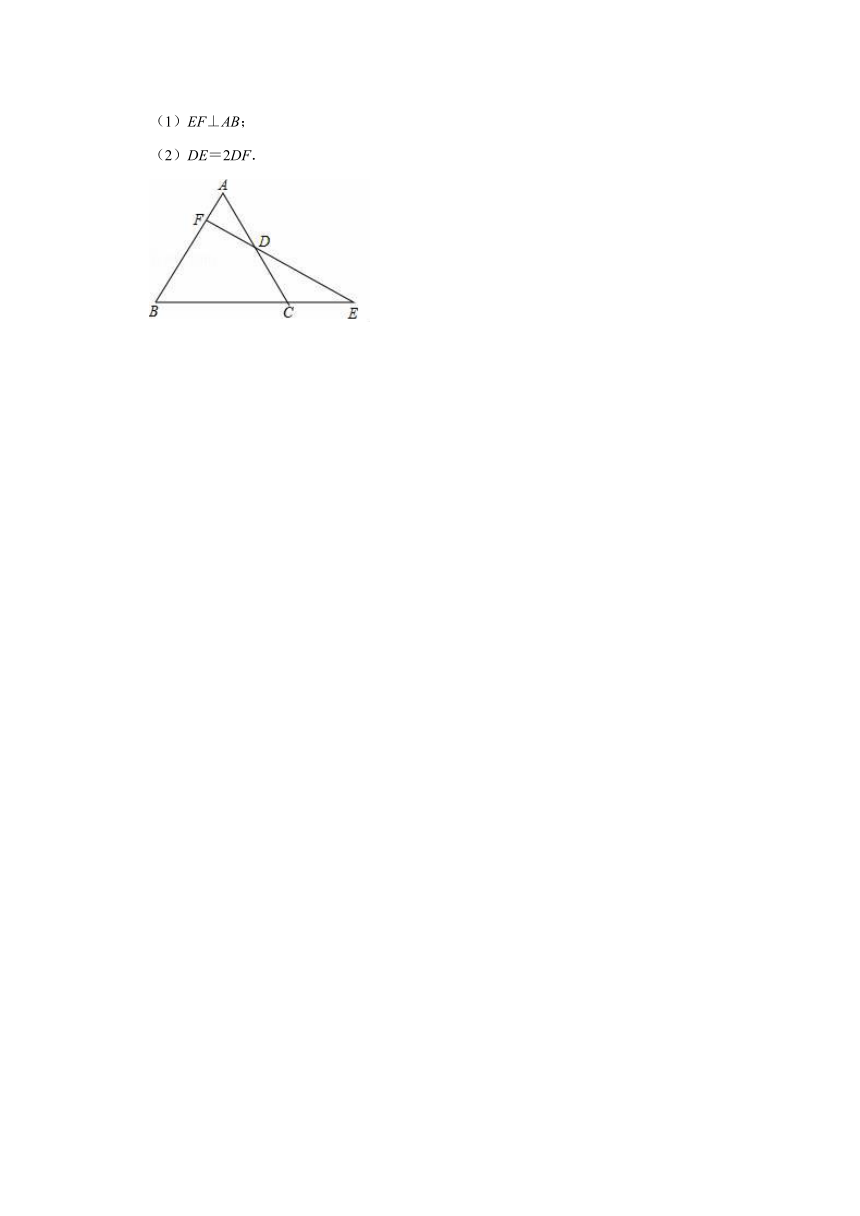
27.如图,△ABC是等边三角形,延长BC到E,使CE=BC.点D是边AC的中点,连接ED并延长ED交AB于F求证:
(1)EF⊥AB;
(2)DE=2DF.
参考答案与试题解析
一.选择题(共12小题,满分48分,每小题4分)
1.解:原式=××
=,
故选:B.
2.解:∵,即,
∴x=±1,
又∵x≠1,
∴x=﹣1.
故选:B.
3.解:A、等腰三角形是轴对称图形,是真命题;
B、三角形的外角大于与它不相邻的一个内角,是假命题;
C、三角形的中线是一条线段,是真命题;
D、两边及其夹角分别相等的两三角形全等,是真命题;
故选:B.
4.解:A、添加BC=BE,可根据SAS判定△ABC≌△DBE,故正确;
B、添加AC=DE,SSA不能判定△ABC≌△DBE,故错误;
C、添加∠A=∠D,可根据ASA判定△ABC≌△DBE,故正确;
D、添加∠ACB=∠DEB,可根据AAS判定△ABC≌△DBE,故正确.
故选:B.
5.解:,,是无理数,是有理数,
故选:B.
6.解:∵的小数部分为b,
∴b=﹣2,
把b=﹣2代入式子(4+b)b中,
原式=(4+b)b=(4+﹣2)×(﹣2)=3.
故选:C.
7.解:根据图示,可得:
a<0<b.
故选:A.
8.解:由3x+10≤1,解得x≤﹣3,
故选:C.
9.解:解不等式3+x>1,得:x>﹣2,
解不等式2x﹣3≤1,得:x≤2,
则不等式组的解集为﹣2<x≤2,
所以不等式组的整数解有﹣1、0、1、2这4个,
故选:C.
10.解:设导火线的长度为x厘米,可列不等式:
400÷5<x÷1.2,
解得x>96厘米.
故选:D.
11.解:∵=x﹣5,
∴5﹣x≤0
∴x≥5.
故选:C.
12.解:∵x+y=﹣5,xy=3,
∴x<0,y<0,
∴原式=x+y
=+(x<0,y<0)
=+
=﹣2,
当xy=3时,原式=﹣2.
故选:B.
二.填空题(共8小题,满分32分,每小题4分)
13.解:原式=,
故答案为:.
14.解:∵原命题的条件是:“相等的角”,结论是:“这两个角是对顶角”,
∴命题“相等的角是对顶角”写成“如果,那么”的形式为:“如果两个角相等,那么两个角是对顶角”
故答案为:如果两个角相等,那么两个角是对顶角.
15.解:∵D,E分别是△ABC的边AB,AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,DE=BC,
∴△ADE∽△ABC,
∴=()2=,
∵△ADE的面积为1,
∴△ABC的面积为4,
故答案为:4.
16.解:﹣=2﹣3=﹣1
故答案为:﹣1.
17.解:设第三边为a,根据三角形的三边关系知,4﹣2<a<4+2.
即2<a<6,
由周长为偶数,
则a为4.
故答案为:4.
18.解:由题意可知2x﹣4≥0,当x=2时,取得最小值0
故答案是:2.
19.解:∵a=﹣0.32=﹣0.09,b=﹣3﹣2=﹣,c=(﹣)﹣2=9,d=(﹣)0=1,
∴b<a<d<c,
故答案为:b<a<d<c
20.解:某不等式组的解集是﹣2≤x<1,
符合该不等式组的整数解为:﹣2,﹣1,0;
故答案为:﹣2、﹣1、0.
三.解答题(共7小题,满分70分)
21.解:原式=9﹣1+×2﹣+3﹣
=9﹣1+﹣+3﹣
=10.
22.解:原式=(+)?
=?
=2(x+2)
=2x+4,
当x=﹣时,
原式=2×(﹣)+4
=﹣1+4
=3.
23.证明:过点D作DE⊥AB于E,DF⊥AC于F,则∠DEB=∠DFC=90°.
∵AD是中线
∴BD=CD,S△ABD=S△ACD,
∵∠B=∠C
在△DEB与△DFC中
,
∴△DEB≌△DFC(AAS)
∴DE=DF
∴根据S△ABD=S△ACD得:
?AB?DE=?AC?DF,
∴AB=AC.
24.解:∵|x+|+(y﹣)2=0,
∴x=﹣,y=,
则原式=(﹣×)1999=(﹣1)1999=﹣1.
25.解:设能购进A型号净水器x台,
根据题意知,600x+800(160﹣x)≥116000,
解得:x≤60,
答:A型号家用净水器最多能购进60台.
26.解:(1)由题意,得
,
解得
即x的值为1800,y的值为3;
(2)设某营业员当月卖服装m件,由题意得,
1800+3m≥3100,
解得,,
∵m只能为正整数,
∴m最小为434,
即某营业员当月至少要卖434件;
(3)设一件甲为a元,一件乙为b元,一件丙为c元,则
,
将两等式相加得,4a+4b+4c=720,
则a+b+c=180,
即购买一件甲、一件乙、一件丙共需180元.
27.证明:(1)∵△ABC是等边三角形,
∴AC=BC,∠ACB=∠B=60°,
∵D为AC的中点,
∴AD=CD=AC,
∵CE=BC,
∴CD=CE,
∵∠E+∠CDE=∠ACB=60°,
∴∠E=∠CDE=30°,
∵∠B=60°,
∴∠EFB=180°﹣60°﹣30°=90°,
即EF⊥AB;
(2)连接BD,
∵△ABC是等边三角形,
∴AB=BC,∠ABC=60°,
∵D为AC的中点,
∴∠DBC=∠ABD=ABC=30°,
∵∠E=30°,
∴∠DBC=∠E,
∴DE=BD,
∵∠BFE=90°,∠ABD=30°,
∴BD=2DF,
即DE=2DF.
一.选择题(共12小题,满分48分,每小题4分)
1.计算的结果为( )
A.
B.
C.
D.
2.能使分式的值为零的所有x的值是( )
A.x=1
B.x=﹣1
C.x=1或x=﹣1
D.x=2或x=1
3.下列命题中,为假命题的是( )
A.等腰三角形是轴对称图形
B.三角形的外角大于它的每一个内角
C.三角形的中线是一条线段
D.两边及其夹角分别相等的两三角形全等
4.如图,AB=DB,∠1=∠2,请问添加下面哪个条件不能判断△ABC≌△DBE的是( )
A.BC=BE
B.AC=DE
C.∠A=∠D
D.∠ACB=∠DEB
5.下列各数中,有理数是( )
A.
B.
C.
D.
6.设的小数部分为b,那么(4+b)b的值是( )
A.1
B.是一个有理数
C.3
D.无法确定
7.实数a,b在数轴上的对应点的位置如图所示,把a,b,0按照从小到大的顺序排列,正确的是( )
A.a<0<b
B.0<a<b
C.b<0<a
D.0<b<a
8.不等式3x+10≤1的解集在数轴上表示正确的是( )
A.
B.
C.
D.
9.不等式组的整数解的个数是( )
A.2
B.3
C.4
D.5
10.在四川抗震救灾中,某抢险地段需实行爆破.操作人员点燃导火线后,要在炸药爆炸前跑到400米以外的安全区域.已知导火线的燃烧速度是1.2厘米/秒,操作人员跑步的速度是5米/秒.为了保证操作人员的安全,导火线的长度要超过( )
A.66厘米
B.76厘米
C.86厘米
D.96厘米
11.若=x﹣5,则x的取值范围是( )
A.x<5
B.x≤5
C.x≥5
D.x>5
12.已知,x+y=﹣5,xy=3,则的结果是( )
A.
B.﹣
C.
D.﹣
二.填空题(共8小题,满分32分,每小题4分)
13.计算:
?=
.
14.把命题“相等的角是对顶角”改写成“如果…,那么…”的形式是
.
15.如图,D,E分别是△ABC的边AB,AC的中点,若△ADE的面积为1,则△ABC的面积等于
.
16.计算﹣等于
.
17.三角形两边长分别是2,4,第三边长为偶数,第三边长为
.
18.当x=
时,的值最小.
19.若a=﹣0.32,b=﹣3﹣2,c=(﹣)﹣2,d=(﹣)0,请用“<”将a、b、c、d连起来:
.
20.如果某不等式组的解集是﹣2≤x<1,那么该不等式组的整数解是
.
三.解答题(共7小题,满分70分)
21.计算:.
22.先化简,再求值:(x﹣2+)÷,其中x=﹣.
23.一节数学课上,老师布置了一道课堂练习:“如图,在△ABC中,∠B=∠C,求证:AB=AC“,小明发现,他取BC的中点D,连接AD后,无法证明△ABD≌△ACD,故举手提问老师,老师听了他的困惑,告诉他只要再作两条垂线段就可以证明了,你知道如何继续证明吗?请你写下完整的证明过程.
24.若:,则:(x?y)1999等于多少.
25.为提高饮水质量,越来越多的居民选购家用净水器.一商场抓住商机,从厂家购进了A、B两种型号家用净水器160台,A型号家用净水器进价是1500元/台,售价是2100元/台,B型号家用净水器进价是3500元/台,售价是4300元/台.为保证售完这160台家用净水器的毛利润不低于116000元,求A型号家用净水器最多能购进多少台?(注:毛利润=售价﹣进价)
26.小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
营业员A:月销售件数200件,月总收入2400元;
营业员B:月销售件数300件,月总收入2700元;
假设营业员的月基本工资为x元,销售每件服装奖励y元.
(1)求x、y的值;
(2)若某营业员的月总收入不低于3100元,那么他当月至少要卖服装多少件?
(3)商场为了多销售服装,对顾客推荐一种购买方式:如果购买甲3件,乙2件,丙1件共需350元;如果购买甲1件,乙2件,丙3件共需370元.某顾客想购买甲、乙、丙各一件共需多少元?
27.如图,△ABC是等边三角形,延长BC到E,使CE=BC.点D是边AC的中点,连接ED并延长ED交AB于F求证:
(1)EF⊥AB;
(2)DE=2DF.
参考答案与试题解析
一.选择题(共12小题,满分48分,每小题4分)
1.解:原式=××
=,
故选:B.
2.解:∵,即,
∴x=±1,
又∵x≠1,
∴x=﹣1.
故选:B.
3.解:A、等腰三角形是轴对称图形,是真命题;
B、三角形的外角大于与它不相邻的一个内角,是假命题;
C、三角形的中线是一条线段,是真命题;
D、两边及其夹角分别相等的两三角形全等,是真命题;
故选:B.
4.解:A、添加BC=BE,可根据SAS判定△ABC≌△DBE,故正确;
B、添加AC=DE,SSA不能判定△ABC≌△DBE,故错误;
C、添加∠A=∠D,可根据ASA判定△ABC≌△DBE,故正确;
D、添加∠ACB=∠DEB,可根据AAS判定△ABC≌△DBE,故正确.
故选:B.
5.解:,,是无理数,是有理数,
故选:B.
6.解:∵的小数部分为b,
∴b=﹣2,
把b=﹣2代入式子(4+b)b中,
原式=(4+b)b=(4+﹣2)×(﹣2)=3.
故选:C.
7.解:根据图示,可得:
a<0<b.
故选:A.
8.解:由3x+10≤1,解得x≤﹣3,
故选:C.
9.解:解不等式3+x>1,得:x>﹣2,
解不等式2x﹣3≤1,得:x≤2,
则不等式组的解集为﹣2<x≤2,
所以不等式组的整数解有﹣1、0、1、2这4个,
故选:C.
10.解:设导火线的长度为x厘米,可列不等式:
400÷5<x÷1.2,
解得x>96厘米.
故选:D.
11.解:∵=x﹣5,
∴5﹣x≤0
∴x≥5.
故选:C.
12.解:∵x+y=﹣5,xy=3,
∴x<0,y<0,
∴原式=x+y
=+(x<0,y<0)
=+
=﹣2,
当xy=3时,原式=﹣2.
故选:B.
二.填空题(共8小题,满分32分,每小题4分)
13.解:原式=,
故答案为:.
14.解:∵原命题的条件是:“相等的角”,结论是:“这两个角是对顶角”,
∴命题“相等的角是对顶角”写成“如果,那么”的形式为:“如果两个角相等,那么两个角是对顶角”
故答案为:如果两个角相等,那么两个角是对顶角.
15.解:∵D,E分别是△ABC的边AB,AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,DE=BC,
∴△ADE∽△ABC,
∴=()2=,
∵△ADE的面积为1,
∴△ABC的面积为4,
故答案为:4.
16.解:﹣=2﹣3=﹣1
故答案为:﹣1.
17.解:设第三边为a,根据三角形的三边关系知,4﹣2<a<4+2.
即2<a<6,
由周长为偶数,
则a为4.
故答案为:4.
18.解:由题意可知2x﹣4≥0,当x=2时,取得最小值0
故答案是:2.
19.解:∵a=﹣0.32=﹣0.09,b=﹣3﹣2=﹣,c=(﹣)﹣2=9,d=(﹣)0=1,
∴b<a<d<c,
故答案为:b<a<d<c
20.解:某不等式组的解集是﹣2≤x<1,
符合该不等式组的整数解为:﹣2,﹣1,0;
故答案为:﹣2、﹣1、0.
三.解答题(共7小题,满分70分)
21.解:原式=9﹣1+×2﹣+3﹣
=9﹣1+﹣+3﹣
=10.
22.解:原式=(+)?
=?
=2(x+2)
=2x+4,
当x=﹣时,
原式=2×(﹣)+4
=﹣1+4
=3.
23.证明:过点D作DE⊥AB于E,DF⊥AC于F,则∠DEB=∠DFC=90°.
∵AD是中线
∴BD=CD,S△ABD=S△ACD,
∵∠B=∠C
在△DEB与△DFC中
,
∴△DEB≌△DFC(AAS)
∴DE=DF
∴根据S△ABD=S△ACD得:
?AB?DE=?AC?DF,
∴AB=AC.
24.解:∵|x+|+(y﹣)2=0,
∴x=﹣,y=,
则原式=(﹣×)1999=(﹣1)1999=﹣1.
25.解:设能购进A型号净水器x台,
根据题意知,600x+800(160﹣x)≥116000,
解得:x≤60,
答:A型号家用净水器最多能购进60台.
26.解:(1)由题意,得
,
解得
即x的值为1800,y的值为3;
(2)设某营业员当月卖服装m件,由题意得,
1800+3m≥3100,
解得,,
∵m只能为正整数,
∴m最小为434,
即某营业员当月至少要卖434件;
(3)设一件甲为a元,一件乙为b元,一件丙为c元,则
,
将两等式相加得,4a+4b+4c=720,
则a+b+c=180,
即购买一件甲、一件乙、一件丙共需180元.
27.证明:(1)∵△ABC是等边三角形,
∴AC=BC,∠ACB=∠B=60°,
∵D为AC的中点,
∴AD=CD=AC,
∵CE=BC,
∴CD=CE,
∵∠E+∠CDE=∠ACB=60°,
∴∠E=∠CDE=30°,
∵∠B=60°,
∴∠EFB=180°﹣60°﹣30°=90°,
即EF⊥AB;
(2)连接BD,
∵△ABC是等边三角形,
∴AB=BC,∠ABC=60°,
∵D为AC的中点,
∴∠DBC=∠ABD=ABC=30°,
∵∠E=30°,
∴∠DBC=∠E,
∴DE=BD,
∵∠BFE=90°,∠ABD=30°,
∴BD=2DF,
即DE=2DF.
同课章节目录
