29.3 课题学习 制作立体模型 同步练习(含答案)
文档属性
| 名称 | 29.3 课题学习 制作立体模型 同步练习(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 06:47:55 | ||
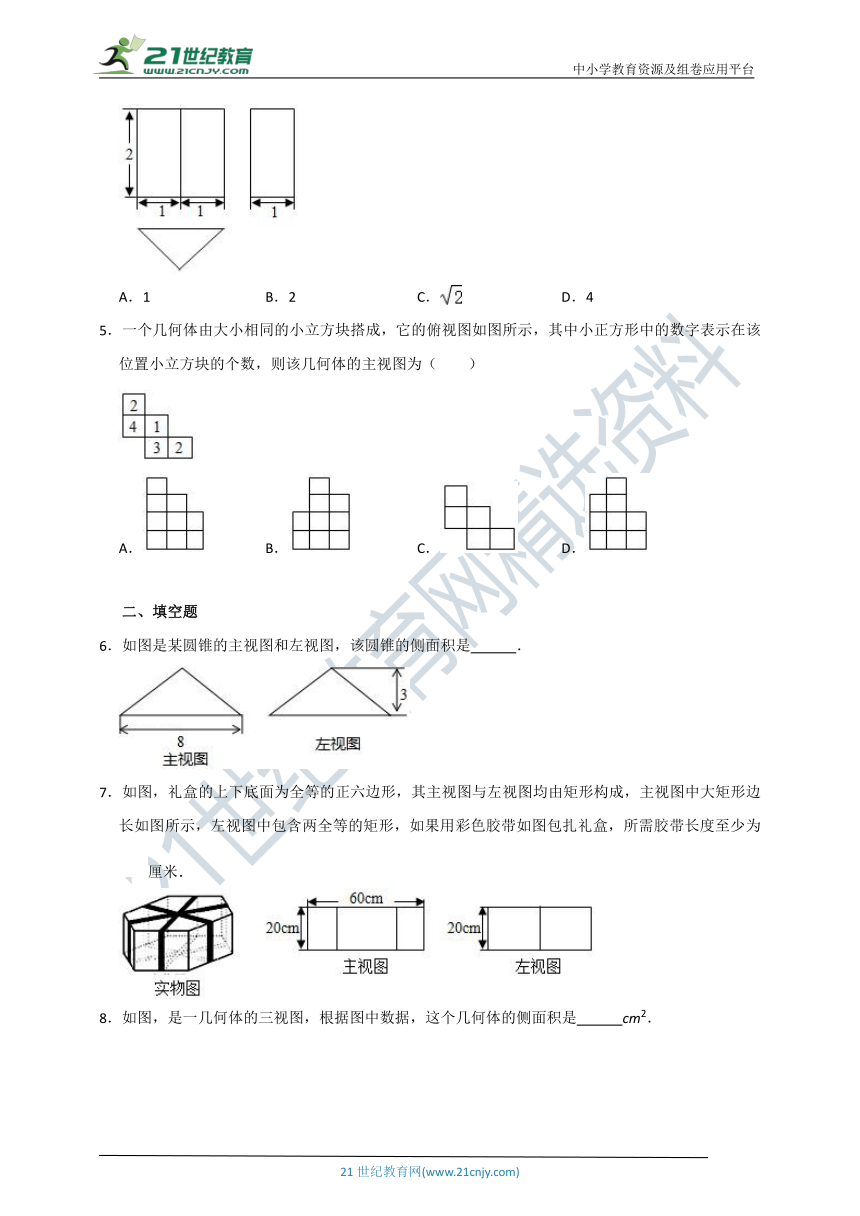
图片预览

文档简介
中小学教育资源及组卷应用平台
第29章投影与视图
29.3 课题学习 制作立体模型
选择题
1.如图所示的主视图对应的几何体是( )
A. B. C. D.
2.如图是由5个立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上的小立方块的个数,则这个几何体的主视图是( )
A. B. C. D.
3.如图,是一个几何体的三视图,则这个几何体是( )
A. B.
C. D.
4.如图是一个几何体的三视图,则该几何体的体积为( )
A.1 B.2 C. D.4
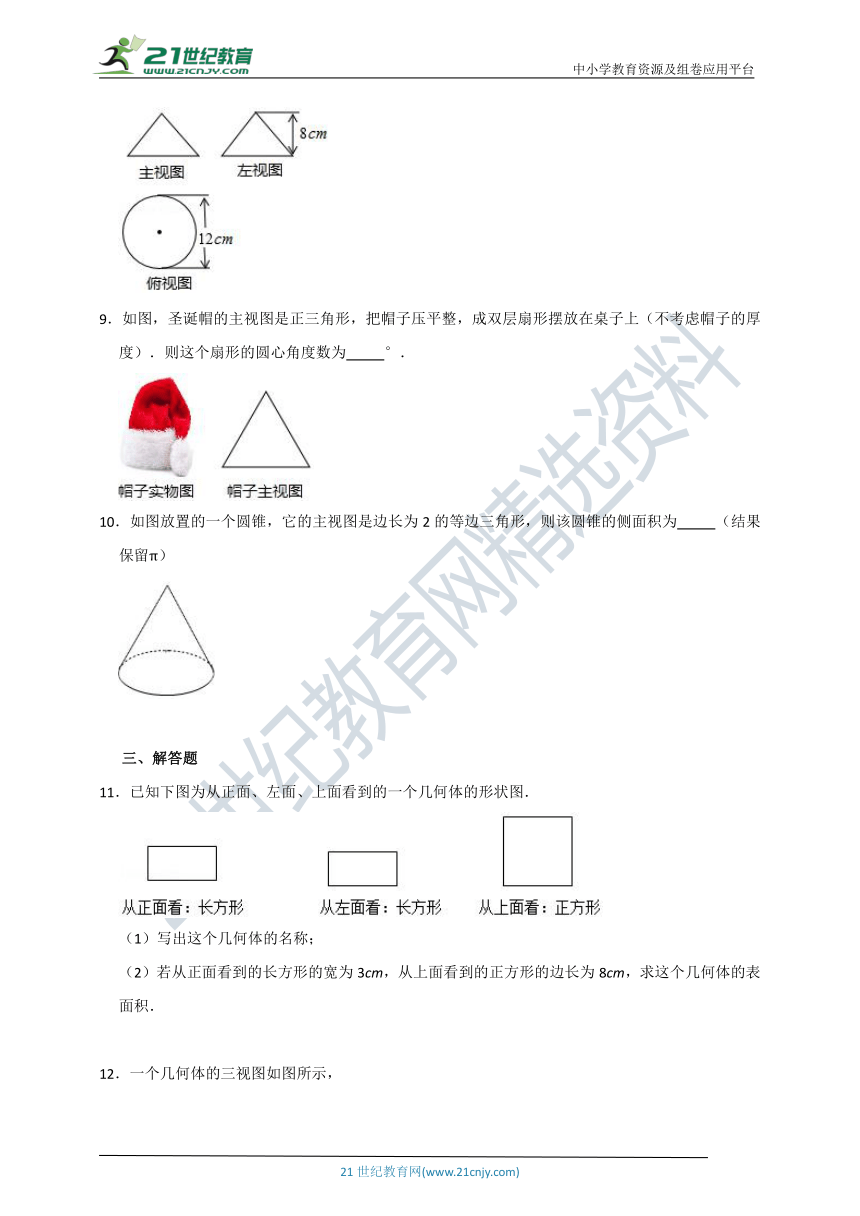
5.一个几何体由大小相同的小立方块搭成,它的俯视图如图所示,其中小正方形中的数字表示在该位置小立方块的个数,则该几何体的主视图为( )
A. B. C. D.
填空题
6.如图是某圆锥的主视图和左视图,该圆锥的侧面积是 .
7.如图,礼盒的上下底面为全等的正六边形,其主视图与左视图均由矩形构成,主视图中大矩形边长如图所示,左视图中包含两全等的矩形,如果用彩色胶带如图包扎礼盒,所需胶带长度至少为 厘米.
8.如图,是一几何体的三视图,根据图中数据,这个几何体的侧面积是 cm2.
9.如图,圣诞帽的主视图是正三角形,把帽子压平整,成双层扇形摆放在桌子上(不考虑帽子的厚度).则这个扇形的圆心角度数为 °.
10.如图放置的一个圆锥,它的主视图是边长为2的等边三角形,则该圆锥的侧面积为 (结果保留π)
解答题
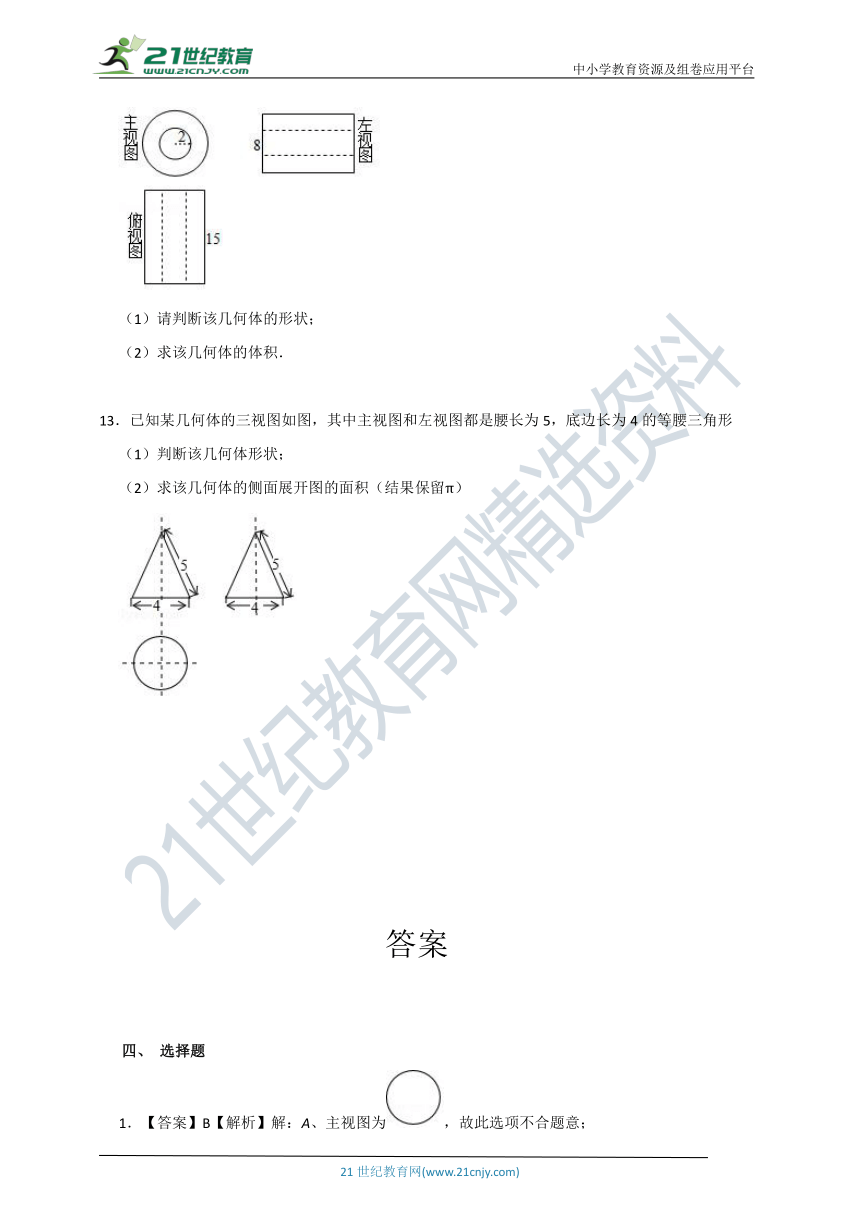
11.已知下图为从正面、左面、上面看到的一个几何体的形状图.
(1)写出这个几何体的名称;
(2)若从正面看到的长方形的宽为3cm,从上面看到的正方形的边长为8cm,求这个几何体的表面积.
12.一个几何体的三视图如图所示,
(1)请判断该几何体的形状;
(2)求该几何体的体积.
13.已知某几何体的三视图如图,其中主视图和左视图都是腰长为5,底边长为4的等腰三角形
(1)判断该几何体形状;
(2)求该几何体的侧面展开图的面积(结果保留π)
答案
选择题
1.【答案】B【解析】解:A、主视图为,故此选项不合题意;
B、主视图为,故此选项符合题意;
C、主视图为,故此选项不合题意;
D、主视图为,故此选项不合题意.
故选:B.
2.【答案】A【解析】解:从正面看去,一共三列,左边有1个小正方形,中间有2个小正方形,右边有1个小正方形,主视图是.
故选:A.
3.【答案】B
【解析】解:结合三个视图发现,这个几何体是长方体和圆锥的组合图形.
故选:B.
4.如图是一个几何体的三视图,则该几何体的体积为( )
A.1 B.2 C. D.4
【答案】B
【解析】解:(1+1)×1÷2×2
=2×1÷2×2
=2.
故该几何体的体积为2.
故选:B.
5.【答案】A【解析】解:从正面看所得到的图形为.
故选:A.
填空题
6.【答案】20π.【解析】解:由题可得,圆锥的底面直径为8,高为3,
则圆锥的底面周长为8π,
圆锥的母线长为=5,
则圆锥的侧面积=×8π×5=20π.
故答案为:20π.
7.【答案】(180+120).
【解析】解:根据题意,作出实际图形的上底,
如图:AC,CD是上底面的两边.
则AC=60÷2=30(cm),∠ACD=120°,
作CB⊥AD于点B,
那么AB=AC×sin60°=15(cm),
所以AD=2AB=30(cm),
胶带的长至少=30×6+20×6=(180+120)(cm).
故答案为:(180+120).
8.【答案】60π.【解析】解:由三视图可知,原几何体为圆锥,
∵l==10,
∴S侧=×πd×l=×π×12×10=60π.
故答案为:60π.
9.【答案】90【解析】解:设正三角形的边长为a,双层扇形的圆心角为n.
∴圆锥的底面圆的周长=πa,
由题意:πa=,
∴n=90°.
故答案为:90.
10.【答案】2π.
【解析】解:根据题意,圆锥的侧面积=rl=×2×2π=2π.
故答案为:2π.
解答题
11.【答案】解:(1)这个几何体的名称是长方体(四棱柱);
(2)S=8×8×2+8×3×4=64×2+24×4=224(cm2).
故这个几何体的表面积是224cm2.
12.【答案】解:(1)由三视图可知该几何体是一个内半径是2,外半径是4,高为15的空心圆柱体;
(2)该几何体的体积为:(π?42﹣π?22)×15=180π.
13.【答案】解:(1)由三视图可知,该几何体是圆锥;
(2)侧面展开图的面积=π×2×5=10π.
_21?????????è?????(www.21cnjy.com)_
第29章投影与视图
29.3 课题学习 制作立体模型
选择题
1.如图所示的主视图对应的几何体是( )
A. B. C. D.
2.如图是由5个立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上的小立方块的个数,则这个几何体的主视图是( )
A. B. C. D.
3.如图,是一个几何体的三视图,则这个几何体是( )
A. B.
C. D.
4.如图是一个几何体的三视图,则该几何体的体积为( )
A.1 B.2 C. D.4
5.一个几何体由大小相同的小立方块搭成,它的俯视图如图所示,其中小正方形中的数字表示在该位置小立方块的个数,则该几何体的主视图为( )
A. B. C. D.
填空题
6.如图是某圆锥的主视图和左视图,该圆锥的侧面积是 .
7.如图,礼盒的上下底面为全等的正六边形,其主视图与左视图均由矩形构成,主视图中大矩形边长如图所示,左视图中包含两全等的矩形,如果用彩色胶带如图包扎礼盒,所需胶带长度至少为 厘米.
8.如图,是一几何体的三视图,根据图中数据,这个几何体的侧面积是 cm2.
9.如图,圣诞帽的主视图是正三角形,把帽子压平整,成双层扇形摆放在桌子上(不考虑帽子的厚度).则这个扇形的圆心角度数为 °.
10.如图放置的一个圆锥,它的主视图是边长为2的等边三角形,则该圆锥的侧面积为 (结果保留π)
解答题
11.已知下图为从正面、左面、上面看到的一个几何体的形状图.
(1)写出这个几何体的名称;
(2)若从正面看到的长方形的宽为3cm,从上面看到的正方形的边长为8cm,求这个几何体的表面积.
12.一个几何体的三视图如图所示,
(1)请判断该几何体的形状;
(2)求该几何体的体积.
13.已知某几何体的三视图如图,其中主视图和左视图都是腰长为5,底边长为4的等腰三角形
(1)判断该几何体形状;
(2)求该几何体的侧面展开图的面积(结果保留π)
答案
选择题
1.【答案】B【解析】解:A、主视图为,故此选项不合题意;
B、主视图为,故此选项符合题意;
C、主视图为,故此选项不合题意;
D、主视图为,故此选项不合题意.
故选:B.
2.【答案】A【解析】解:从正面看去,一共三列,左边有1个小正方形,中间有2个小正方形,右边有1个小正方形,主视图是.
故选:A.
3.【答案】B
【解析】解:结合三个视图发现,这个几何体是长方体和圆锥的组合图形.
故选:B.
4.如图是一个几何体的三视图,则该几何体的体积为( )
A.1 B.2 C. D.4
【答案】B
【解析】解:(1+1)×1÷2×2
=2×1÷2×2
=2.
故该几何体的体积为2.
故选:B.
5.【答案】A【解析】解:从正面看所得到的图形为.
故选:A.
填空题
6.【答案】20π.【解析】解:由题可得,圆锥的底面直径为8,高为3,
则圆锥的底面周长为8π,
圆锥的母线长为=5,
则圆锥的侧面积=×8π×5=20π.
故答案为:20π.
7.【答案】(180+120).
【解析】解:根据题意,作出实际图形的上底,
如图:AC,CD是上底面的两边.
则AC=60÷2=30(cm),∠ACD=120°,
作CB⊥AD于点B,
那么AB=AC×sin60°=15(cm),
所以AD=2AB=30(cm),
胶带的长至少=30×6+20×6=(180+120)(cm).
故答案为:(180+120).
8.【答案】60π.【解析】解:由三视图可知,原几何体为圆锥,
∵l==10,
∴S侧=×πd×l=×π×12×10=60π.
故答案为:60π.
9.【答案】90【解析】解:设正三角形的边长为a,双层扇形的圆心角为n.
∴圆锥的底面圆的周长=πa,
由题意:πa=,
∴n=90°.
故答案为:90.
10.【答案】2π.
【解析】解:根据题意,圆锥的侧面积=rl=×2×2π=2π.
故答案为:2π.
解答题
11.【答案】解:(1)这个几何体的名称是长方体(四棱柱);
(2)S=8×8×2+8×3×4=64×2+24×4=224(cm2).
故这个几何体的表面积是224cm2.
12.【答案】解:(1)由三视图可知该几何体是一个内半径是2,外半径是4,高为15的空心圆柱体;
(2)该几何体的体积为:(π?42﹣π?22)×15=180π.
13.【答案】解:(1)由三视图可知,该几何体是圆锥;
(2)侧面展开图的面积=π×2×5=10π.
_21?????????è?????(www.21cnjy.com)_
