28.2.2 解直角三角形应用举例 同步练习(含答案)
文档属性
| 名称 | 28.2.2 解直角三角形应用举例 同步练习(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 06:46:17 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第28章 锐角三角函数
28.2.2 应用举例
选择题
1.如图,河坝横断面迎水坡AB的坡比为1:,坝高BC=3m,则AB的长度为( )
A.6m B.3m C.9m D.6m
2.如图,坡角为27°的斜坡上两根电线杆间的坡面距离为80米,则这两根电线杆间的水平距离为( )
A.米 B.80cos27°米 C.80tan27°米 D.米
3.如图,重庆建川博物馆的主题雕塑“冒着敌人的炮火”矗立在鹅公岩长江大桥旁,为了测量雕塑AE的大致高度,小南同学在点C处测得雕塑顶部A的仰角为45°,雕塑底部E的仰角为37°,再沿着CB方向走8米到达点D,此时测得雕塑顶部A的仰角为54.5°,小南同学的身高忽略不计,已知A、B、C、D、E在同一平面内,则该雕塑AE的高度约为( )米.(参考敷据:tan37°≈0.75,tan54.5°≈1.40)
A.7 B.8 C.21 D.28
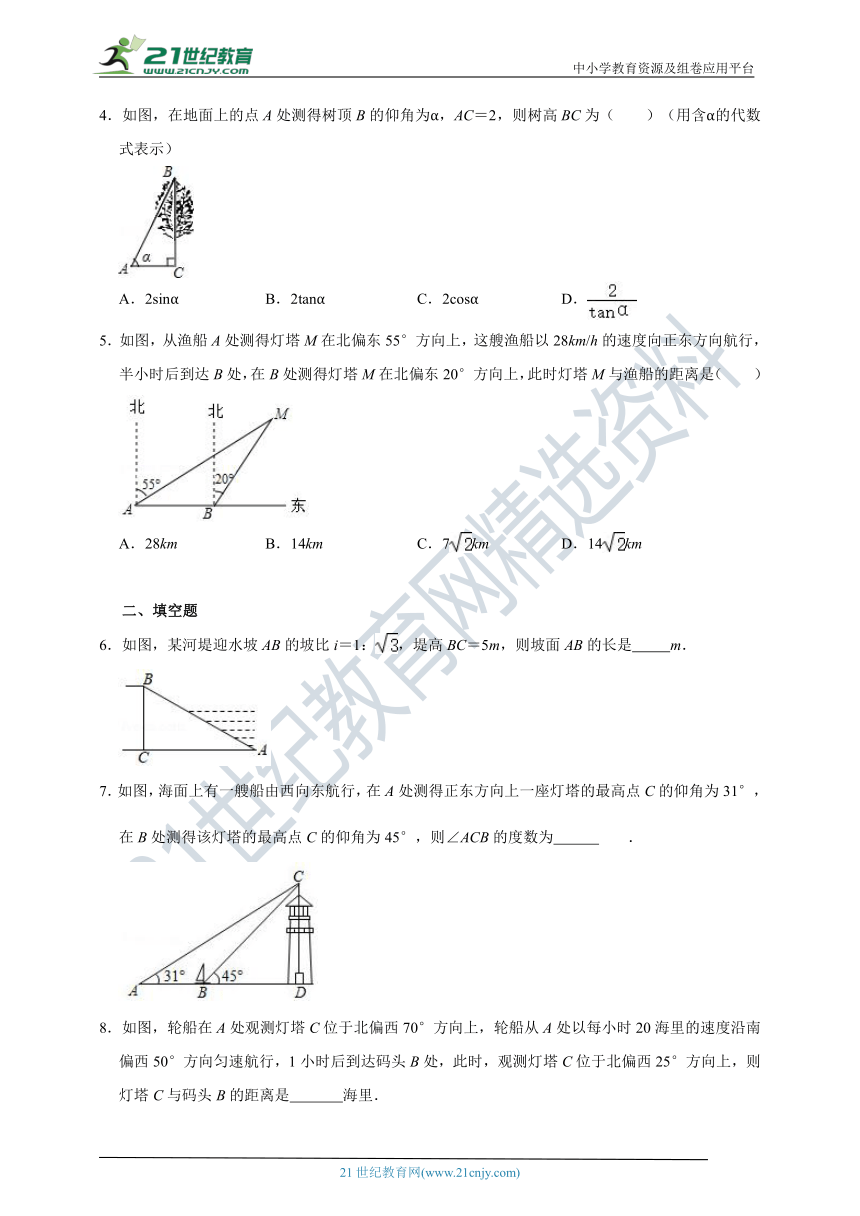
4.如图,在地面上的点A处测得树顶B的仰角为α,AC=2,则树高BC为( )(用含α的代数式表示)
A.2sinα B.2tanα C.2cosα D.
5.如图,从渔船A处测得灯塔M在北偏东55°方向上,这艘渔船以28km/h的速度向正东方向航行,半小时后到达B处,在B处测得灯塔M在北偏东20°方向上,此时灯塔M与渔船的距离是( )
A.28km B.14km C.7km D.14km
填空题
6.如图,某河堤迎水坡AB的坡比i=1:,堤高BC=5m,则坡面AB的长是 m.
7.如图,海面上有一艘船由西向东航行,在A处测得正东方向上一座灯塔的最高点C的仰角为31°,在B处测得该灯塔的最高点C的仰角为45°,则∠ACB的度数为 .
8.如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是 海里.
9.如图,甲,乙两艘船同时从港口A出发,甲船沿北偏东45°的方向前进,乙船沿北偏东75°方向以每小时30海里的速度前进,两船航行两小时分别到达B,C处,此时测得甲船在乙船的正西方向,则甲船每小时行驶 海里.
10.如图,小明为测量大树MN的高度,在点A处测得大树顶端M的仰角是30°,沿NA的方向后退50米到达点B,测得大树顶端M的仰角是15°,A,B,N在同一水平线上,若小明的身高忽略不计,则大树高约为 米.
解答题
11.如图是某货站传送货物的平面示意图,为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4m.
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出5m的通道,试判断距离B点4m的货物MNQP是否需要挪走,并说明理由.
12.西安市某学校的数学探究小组利用无人机在操场上开展测量教学楼高度的活动,如图,无人机从A处观测,测得教学楼顶点O的俯角为22°,继续水平前行10米到达B处,测得俯角为45°,已知无人机的飞行高度为31米,则这栋教学楼的高度是多少米?(精确到0.1米)(参考数据:sin22°≈,cos22°≈,tan22°≈)
13.某公园中有条东西走向的小河,河宽固定,小河南岸边上有一块石墩A,北岸边上有一棵大树P,小杨利用它们测量小河的宽度,于是,他去了河边,如图.他从河的南岸石墩A处测得大树P在其北偏东30°方向,然后他沿正东方向步行80米到达点B处,此时测得大树P在其北偏西60°方向.请根据以上所测得的数据,计算小河的宽度.(结果保留根号)
14.如图,一艘渔船以40海里/小时的速度由西向东追赶鱼群,在A处测得小岛C在渔船的北偏东60°方向;半小时后,渔船到达B处,此时测得小岛C在渔船的北偏东30°方向.已知以小岛C为中心,周围18海里以内为军事演习着弹危险区.如果这艘渔船继续向东追赶鱼群,是否有着弹危险?
答案
1.A.2.B.3.A.4.B.5.B.
6.【答案】10
【解析】解:∵坡比i=tan∠CAB===,∠ACB=90°,
∴∠BAC=30°,
∴AB=2BC,
又∵BC=5m,
∴AB=2BC=10m,
故答案为:10.
7.【答案】14°.
【解析】解:由题意得:∠BAC=31°,∠CBD=45°,
∵∠CBD=∠BAC+∠ACB,
∴∠ACB=∠CBD﹣∠BAC=45°﹣31°=14°,
故答案为:14°.
8.【答案】10.
【解析】解:作BD⊥AC于点D,
由题意得,∠CBA=25°+50°=75°,AB=20,
则∠CAB=(90°﹣70°)+(90°﹣50°)=20°+40°=60°,
∴∠ABD=30°,
∴∠CBD=75°﹣30°=45°,
在Rt△ABD中,BD=AB?sin∠CAB=20×sin60°=20×=10,
在Rt△BCD中,∠CBD=45°,
则BC=BD=10×=10,
故答案为:10.
9.【答案】15(﹣1).
【解析】解:设甲船每小时行驶x海里,则AB=2x海里,
如图,
作BD⊥AC于点D,在AC上取点E,使BE=CE,
根据题意可知:
∠BAD=30°,∠C=15°,
∴∠BED=30°,
∴AD=DE=x,
CE=BE=AB=2x,
∴AD+DE+CE=60,
即x+x+2x=60,
解得x=15(﹣1)(海里).
答:甲船每小时行驶15(﹣1)海里.
故答案为:15(﹣1).
10.【答案】25
【解析】解:∠MAN是△ABM的一个外角,
∴∠AMB=∠MAN﹣∠ABM=30°﹣15°=15°,
∴∠AMB=∠ABM,
∴AM=AB=50米,
在Rt△AMN中,∠MAN=30°,
∴MN=AM=25米;
故答案为:25.
11.【答案】解:(1)在Rt△ABD中,∠ABD=45°,
∴AD=AB=4,
在Rt△ACD中,∠ACD=30°,
∴AC=2AD=8,
答:新传送带AC的长度为8m;
(2)在Rt△ACD中,∠ACD=30°,
∴CD=AB?cos∠ACD=4,
在Rt△ABD中,∠ABD=45°,
∴BD=AD=4,
∴BC=CD﹣BD=4﹣4,
∴PC=BP﹣BC=4﹣(4﹣4)=4<5,
∴货物MNQP需要挪走.
12.【答案】解:过O作OC⊥AB交AB的延长线于点C,作OD⊥AE于点E,如图所示:
∵DA⊥AC,OC⊥AB,OD⊥AE,
∴四边形ADOC为矩形,
∴AD=OC,
同理可得:DE=OH,
在Rt△OCB中,∠OBC=45°,
∴OC=BC,
在Rt△OCA中,tan∠OAC=,
∴≈,
解得:OC=,
∴OH=DE=31﹣≈24.3(米),
答:这栋教学楼的高度约为24.3米.
13.【答案】解:如图,作PD⊥AB交CA于点D,
∵∠APD=30°,
∴AD=PD×tan30°=PD,
∵∠BPD=60°,
∴BD=PD×tan60°=PD,
∵AD+BD=80,
∴PD+PD=80,
解得PD=20.
答:这段河的宽为20米.
14.【答案】解:过点C作CD⊥AB交AB的延长线于D,
由题意得,AB=40×=20,∠CAB=30°,∠CBD=60°,
∴∠ACB=∠CBD﹣∠CAB=30°,
∴∠ACB=∠CAB,
∴CB=AB=20,
在Rt△CBD中,sin∠CBD=,
∴CD=BC?sin∠CBD=20×=10,
∵10<18,
∴这艘渔船继续向东追赶鱼群,有着弹危险.
_21?????????è?????(www.21cnjy.com)_
第28章 锐角三角函数
28.2.2 应用举例
选择题
1.如图,河坝横断面迎水坡AB的坡比为1:,坝高BC=3m,则AB的长度为( )
A.6m B.3m C.9m D.6m
2.如图,坡角为27°的斜坡上两根电线杆间的坡面距离为80米,则这两根电线杆间的水平距离为( )
A.米 B.80cos27°米 C.80tan27°米 D.米
3.如图,重庆建川博物馆的主题雕塑“冒着敌人的炮火”矗立在鹅公岩长江大桥旁,为了测量雕塑AE的大致高度,小南同学在点C处测得雕塑顶部A的仰角为45°,雕塑底部E的仰角为37°,再沿着CB方向走8米到达点D,此时测得雕塑顶部A的仰角为54.5°,小南同学的身高忽略不计,已知A、B、C、D、E在同一平面内,则该雕塑AE的高度约为( )米.(参考敷据:tan37°≈0.75,tan54.5°≈1.40)
A.7 B.8 C.21 D.28
4.如图,在地面上的点A处测得树顶B的仰角为α,AC=2,则树高BC为( )(用含α的代数式表示)
A.2sinα B.2tanα C.2cosα D.
5.如图,从渔船A处测得灯塔M在北偏东55°方向上,这艘渔船以28km/h的速度向正东方向航行,半小时后到达B处,在B处测得灯塔M在北偏东20°方向上,此时灯塔M与渔船的距离是( )
A.28km B.14km C.7km D.14km
填空题
6.如图,某河堤迎水坡AB的坡比i=1:,堤高BC=5m,则坡面AB的长是 m.
7.如图,海面上有一艘船由西向东航行,在A处测得正东方向上一座灯塔的最高点C的仰角为31°,在B处测得该灯塔的最高点C的仰角为45°,则∠ACB的度数为 .
8.如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是 海里.
9.如图,甲,乙两艘船同时从港口A出发,甲船沿北偏东45°的方向前进,乙船沿北偏东75°方向以每小时30海里的速度前进,两船航行两小时分别到达B,C处,此时测得甲船在乙船的正西方向,则甲船每小时行驶 海里.
10.如图,小明为测量大树MN的高度,在点A处测得大树顶端M的仰角是30°,沿NA的方向后退50米到达点B,测得大树顶端M的仰角是15°,A,B,N在同一水平线上,若小明的身高忽略不计,则大树高约为 米.
解答题
11.如图是某货站传送货物的平面示意图,为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4m.
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出5m的通道,试判断距离B点4m的货物MNQP是否需要挪走,并说明理由.
12.西安市某学校的数学探究小组利用无人机在操场上开展测量教学楼高度的活动,如图,无人机从A处观测,测得教学楼顶点O的俯角为22°,继续水平前行10米到达B处,测得俯角为45°,已知无人机的飞行高度为31米,则这栋教学楼的高度是多少米?(精确到0.1米)(参考数据:sin22°≈,cos22°≈,tan22°≈)
13.某公园中有条东西走向的小河,河宽固定,小河南岸边上有一块石墩A,北岸边上有一棵大树P,小杨利用它们测量小河的宽度,于是,他去了河边,如图.他从河的南岸石墩A处测得大树P在其北偏东30°方向,然后他沿正东方向步行80米到达点B处,此时测得大树P在其北偏西60°方向.请根据以上所测得的数据,计算小河的宽度.(结果保留根号)
14.如图,一艘渔船以40海里/小时的速度由西向东追赶鱼群,在A处测得小岛C在渔船的北偏东60°方向;半小时后,渔船到达B处,此时测得小岛C在渔船的北偏东30°方向.已知以小岛C为中心,周围18海里以内为军事演习着弹危险区.如果这艘渔船继续向东追赶鱼群,是否有着弹危险?
答案
1.A.2.B.3.A.4.B.5.B.
6.【答案】10
【解析】解:∵坡比i=tan∠CAB===,∠ACB=90°,
∴∠BAC=30°,
∴AB=2BC,
又∵BC=5m,
∴AB=2BC=10m,
故答案为:10.
7.【答案】14°.
【解析】解:由题意得:∠BAC=31°,∠CBD=45°,
∵∠CBD=∠BAC+∠ACB,
∴∠ACB=∠CBD﹣∠BAC=45°﹣31°=14°,
故答案为:14°.
8.【答案】10.
【解析】解:作BD⊥AC于点D,
由题意得,∠CBA=25°+50°=75°,AB=20,
则∠CAB=(90°﹣70°)+(90°﹣50°)=20°+40°=60°,
∴∠ABD=30°,
∴∠CBD=75°﹣30°=45°,
在Rt△ABD中,BD=AB?sin∠CAB=20×sin60°=20×=10,
在Rt△BCD中,∠CBD=45°,
则BC=BD=10×=10,
故答案为:10.
9.【答案】15(﹣1).
【解析】解:设甲船每小时行驶x海里,则AB=2x海里,
如图,
作BD⊥AC于点D,在AC上取点E,使BE=CE,
根据题意可知:
∠BAD=30°,∠C=15°,
∴∠BED=30°,
∴AD=DE=x,
CE=BE=AB=2x,
∴AD+DE+CE=60,
即x+x+2x=60,
解得x=15(﹣1)(海里).
答:甲船每小时行驶15(﹣1)海里.
故答案为:15(﹣1).
10.【答案】25
【解析】解:∠MAN是△ABM的一个外角,
∴∠AMB=∠MAN﹣∠ABM=30°﹣15°=15°,
∴∠AMB=∠ABM,
∴AM=AB=50米,
在Rt△AMN中,∠MAN=30°,
∴MN=AM=25米;
故答案为:25.
11.【答案】解:(1)在Rt△ABD中,∠ABD=45°,
∴AD=AB=4,
在Rt△ACD中,∠ACD=30°,
∴AC=2AD=8,
答:新传送带AC的长度为8m;
(2)在Rt△ACD中,∠ACD=30°,
∴CD=AB?cos∠ACD=4,
在Rt△ABD中,∠ABD=45°,
∴BD=AD=4,
∴BC=CD﹣BD=4﹣4,
∴PC=BP﹣BC=4﹣(4﹣4)=4<5,
∴货物MNQP需要挪走.
12.【答案】解:过O作OC⊥AB交AB的延长线于点C,作OD⊥AE于点E,如图所示:
∵DA⊥AC,OC⊥AB,OD⊥AE,
∴四边形ADOC为矩形,
∴AD=OC,
同理可得:DE=OH,
在Rt△OCB中,∠OBC=45°,
∴OC=BC,
在Rt△OCA中,tan∠OAC=,
∴≈,
解得:OC=,
∴OH=DE=31﹣≈24.3(米),
答:这栋教学楼的高度约为24.3米.
13.【答案】解:如图,作PD⊥AB交CA于点D,
∵∠APD=30°,
∴AD=PD×tan30°=PD,
∵∠BPD=60°,
∴BD=PD×tan60°=PD,
∵AD+BD=80,
∴PD+PD=80,
解得PD=20.
答:这段河的宽为20米.
14.【答案】解:过点C作CD⊥AB交AB的延长线于D,
由题意得,AB=40×=20,∠CAB=30°,∠CBD=60°,
∴∠ACB=∠CBD﹣∠CAB=30°,
∴∠ACB=∠CAB,
∴CB=AB=20,
在Rt△CBD中,sin∠CBD=,
∴CD=BC?sin∠CBD=20×=10,
∵10<18,
∴这艘渔船继续向东追赶鱼群,有着弹危险.
_21?????????è?????(www.21cnjy.com)_
