2020-2021学年苏科版九年级数学上册2.2 圆的对称性2.2.2圆的轴对称性同步习题(word版含解析)
文档属性
| 名称 | 2020-2021学年苏科版九年级数学上册2.2 圆的对称性2.2.2圆的轴对称性同步习题(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 621.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 06:40:50 | ||
图片预览

文档简介
2.2 圆的对称性2.2.2圆的轴对称性
一、选择题(共6小题;共30分)
1. 如图所示,在半径为 5?cm 的 ⊙ O 中,弦 AB=6?cm,OC⊥AB 于点 C,则 OC 等于 ??
A. 3?cm B. 4?cm C. 5?cm D. 6?cm
2. 在 ⊙O 中,圆心 O 到弦 AB 的距离为 AB 长度的一半,则弦 AB 所对圆心角的大小为 ??
A. 30? B. 45? C. 60? D. 90?
3. 如图,在 ⊙O 中,AB,AC 是互相垂直且相等的两条弦,OD⊥AB,OE⊥AC,垂足分别为 D 、 E,若 AC=2?cm,则 ⊙O 的半径为 ??
A. 2?cm B. 2?cm C. 4?cm D. 5?cm
4. 已知点 P 是 ⊙O 内一点,⊙O 的半径为 5,OP=3,在过点 P 的所有 ⊙O 的弦中,弦长为整数的弦的条数为 ??
A. 2 B. 3 C. 4 D. 5
5. 下列说法中,正确的是 ??
A. 平分一条直径的弦必垂直于这条直径
B. 平分一条弧的直线垂直于这条弧所对的弦
C. 弦的垂线必经过这条弦所在圆的圆心
D. 在一个圆内平分一条弧同时平分它所对的弦的直线必经过这个圆的圆心
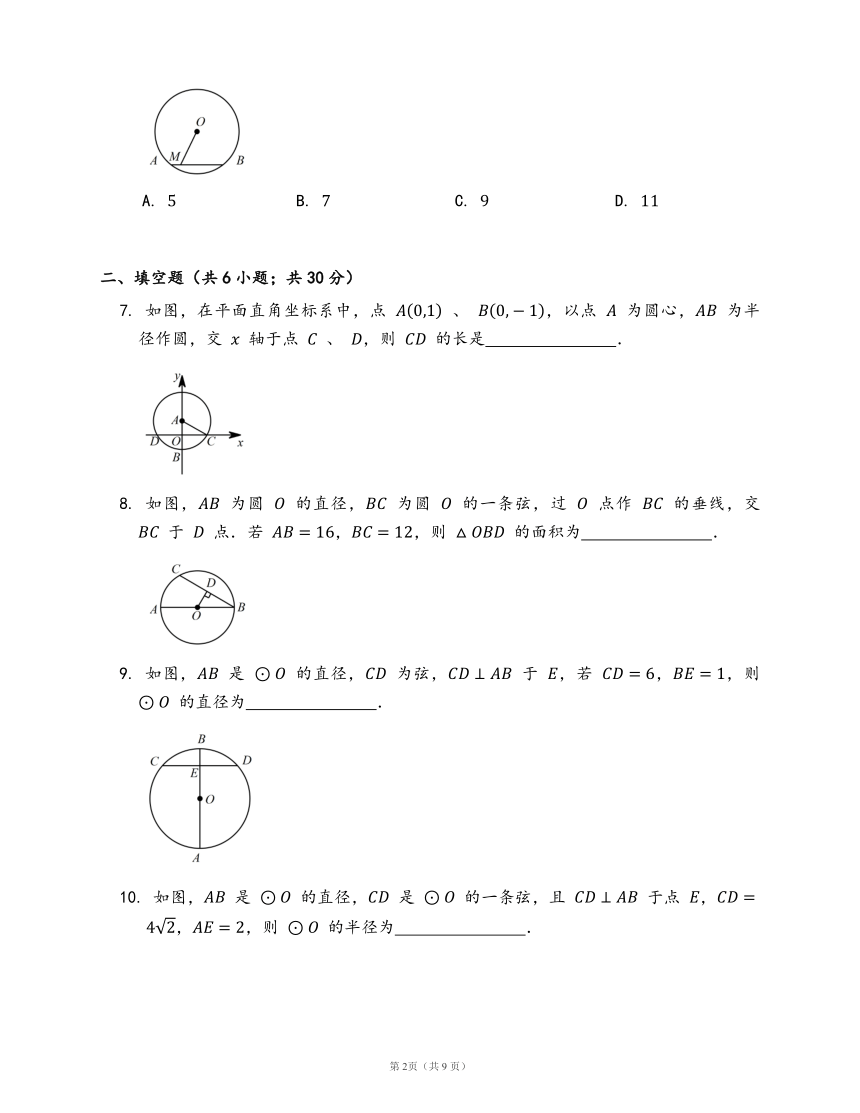
6. 如图,已知 ⊙O 的半径为 10,弦 AB=12,M 是 AB 上任意一点,则线段 OM 的长可能是 ??
A. 5 B. 7 C. 9 D. 11
二、填空题(共6小题;共30分)
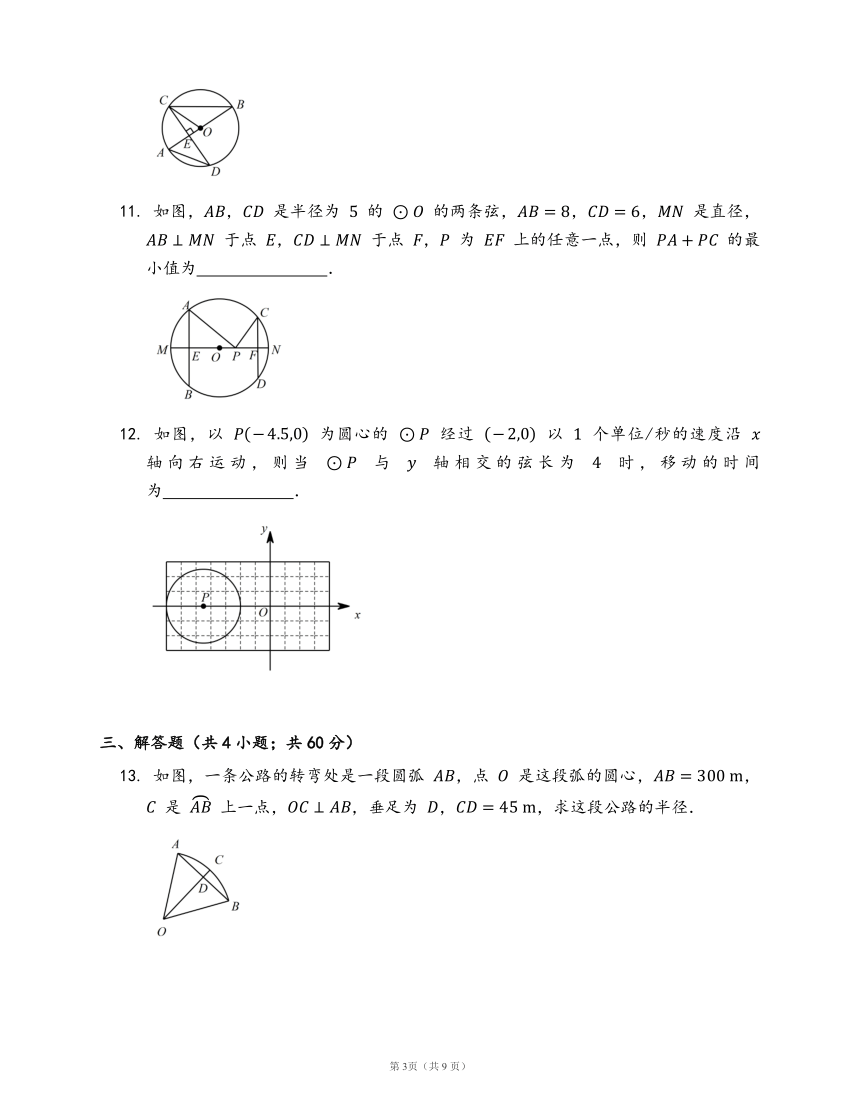
7. 如图,在平面直角坐标系中,点 A0,1 、 B0,-1,以点 A 为圆心,AB 为半径作圆,交 x 轴于点 C 、 D,则 CD 的长是 ?.
8. 如图,AB 为圆 O 的直径,BC 为圆 O 的一条弦,过 O 点作 BC 的垂线,交 BC 于 D 点.若 AB=16,BC=12,则 △OBD 的面积为 ?.
9. 如图,AB 是 ⊙O 的直径,CD 为弦,CD⊥AB 于 E,若 CD=6,BE=1,则 ⊙O 的直径为 ?.
10. 如图,AB 是 ⊙O 的直径,CD 是 ⊙O 的一条弦,且 CD⊥AB 于点 E,CD=42,AE=2,则 ⊙O 的半径为 ?.
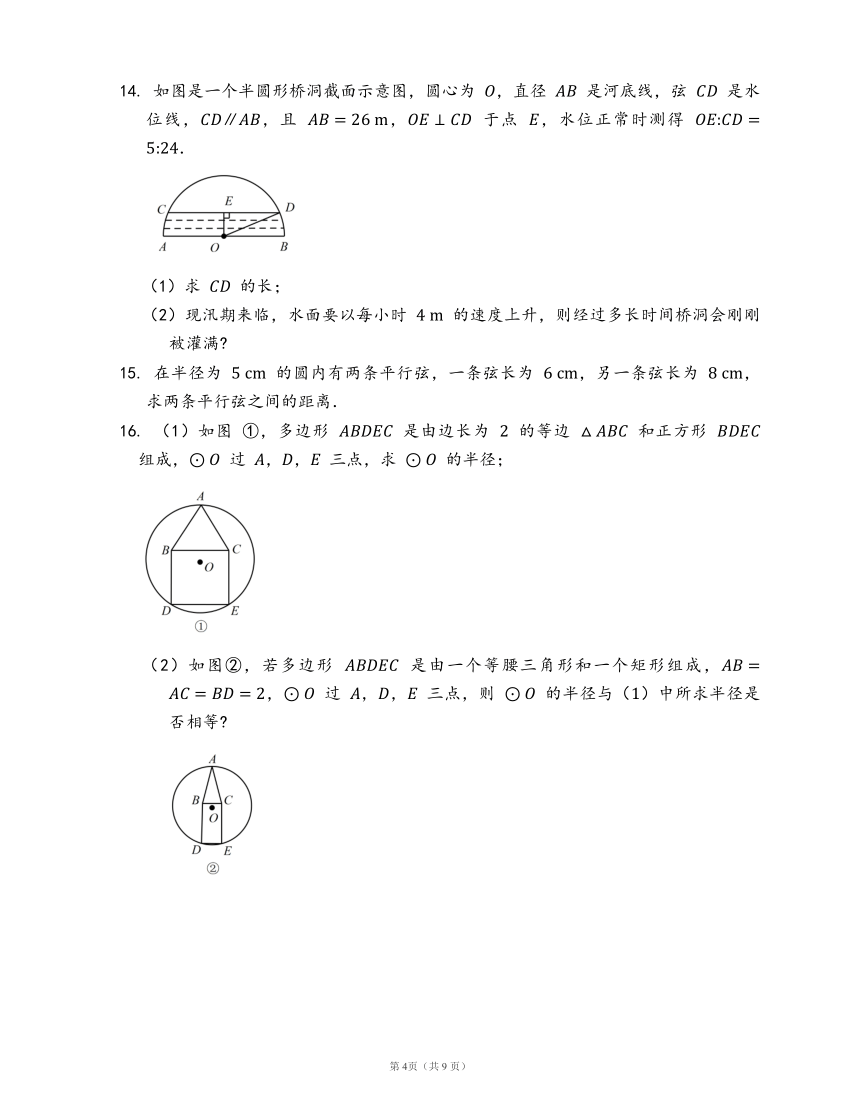
11. 如图,AB,CD 是半径为 5 的 ⊙O 的两条弦,AB=8,CD=6,MN 是直径,AB⊥MN 于点 E,CD⊥MN 于点 F,P 为 EF 上的任意一点,则 PA+PC 的最小值为 ?.
12. 如图,以 P-4.5,0 为圆心的 ⊙P 经过 -2,0 以 1 个单位/秒的速度沿 x 轴向右运动,则当 ⊙P 与 y 轴相交的弦长为 4 时,移动的时间为 ?.
三、解答题(共4小题;共60分)
13. 如图,一条公路的转弯处是一段圆弧 AB,点 O 是这段弧的圆心,AB=300?m,C 是 AB 上一点,OC⊥AB,垂足为 D,CD=45?m,求这段公路的半径.
14. 如图是一个半圆形桥洞截面示意图,圆心为 O,直径 AB 是河底线,弦 CD 是水位线,CD∥AB,且 AB=26?m,OE⊥CD 于点 E,水位正常时测得 OE:CD=5:24.
(1)求 CD 的长;
(2)现汛期来临,水面要以每小时 4?m 的速度上升,则经过多长时间桥洞会刚刚被灌满?
15. 在半径为 5?cm 的圆内有两条平行弦,一条弦长为 6?cm,另一条弦长为 8?cm,求两条平行弦之间的距离.
16. (1)如图 ①,多边形 ABDEC 是由边长为 2 的等边 △ABC 和正方形 BDEC 组成,⊙O 过 A,D,E 三点,求 ⊙O 的半径;
(2)如图②,若多边形 ABDEC 是由一个等腰三角形和一个矩形组成,AB=AC=BD=2,⊙O 过 A,D,E 三点,则 ⊙O 的半径与(1)中所求半径是否相等?
答案
第一部分
1. B
2. D
3. B
4. C
5. D
6. C
第二部分
7. 23
8. 67
【解析】∵OD⊥BC,
∴BD=CD=12BC=12×12=6.
在 Rt△BOD 中,
∵OB=12AB=8,BD=6,
∴OD=OB2-BD2=27,
∴S△OBD=12OD?BD=12×27×6=67.
9. 10
10. 3
【解析】∵ AB 是 ⊙O 的直径,且 CD⊥AB 于点 E,
∴ CE=12CD=12×42=22.
在 Rt△OCE 中,OC2=CE2+OE2,
设 ⊙O 的半径为 r,则 OC=r,OE=OA-AE=r-2,
∴ r2=222+r-22,解得 r=3,
∴ ⊙O 的半径为 3.
11. 72
【解析】连接 OA,OB,OC,作 CH⊥AB 于点 H,连接 BC 与 MN 交于点 P?,则当点 P 在点 P? 的位置时,PA+PC 最小,为 BC 的长.
根据垂径定理,得到 BE=12AB=4,CF=12CD=3,
∴OE=OB2-BE2=52-42=3,OF=OC2-CF2=52-32=4,
∴CH=OE+OF=3+4=7,BH=BE+EH=BE+CF=4+3=7,在 Rt△BCH 中,根据勾股定理得到 BC=72,则 PA+PC 的最小值为 72.
12. 3 秒或 6 秒
【解析】因为以 P-4.5,0 为圆心的 ⊙P 经过 -2,0,
所以 ⊙P 的半径为 2.5.
如图,
因为 AB=4,PE⊥AB,
所以 AE=12AB=2,
所以 PE=PA2-AE2=1.5,同理,PF=1.5,
所以点 E 的坐标为 -3,0,点 F 的坐标为 -6,0,
所以 ⊙P 以 1 个单位/秒的速度沿 x 轴向右运动,则当 ⊙P 与 y 轴相交的弦长为 4 时,则移动的时间为 3 秒或 6 秒.
第三部分
13. 设半径为 r?m,则 OD=r-CD=r-45,
∵OC⊥AB,
∴AD=BD=12AB=150m,
∴ 在 Rt△AOD 中,AO2=AD2+OD2,
即 r2=1502+r-452=22500+r2-90r+2025,
即 90r=24525,解得 r=272.5.
故这段公路的半径是 272.5?m.
14. (1) ∵ 直径 AB=26?m,
∴ OB=12AB=12×26=13m.
∵ OE⊥CD,
∴ DE=12CD.
∵ OE:CD=5:24,
∴ OE:ED=5:12,
设 OE=5x?m,则 ED=12x?m,
∴ 在 Rt△ODE 中,5x2+12x2=132,
解得 x=1,
∴ CD=2DE=2×12×1=24m.
??????(2) 由(1)得 OE=1×5=5m.
延长 OE 交圆 O 于点 F,
∴ EF=OF-OE=13-5=8m.
∴ 84=2小时,即经过 2 小时桥洞会刚刚被灌满.
15. 由题意构造图形,如图,弦 AB=6?cm,弦 CD=8?cm,过圆心 O 作 OE⊥AB 于点 E,且交 CD 于点 F.
因为 AB∥CD,
所以 OF⊥CD,
所以 EF 即为两条平行弦之间的距离.
①当弦 AB 和 CD 在圆心同侧时,如图①所示.
因为 AB=6?cm,CD=8?cm,
所以 AE=3?cm,CF=4?cm.
因为 OA=OC=5?cm,
所以 EO=4?cm,OF=3?cm,
所以 EF=OE-OF=1?cm.
②当弦 AB 和 CD 在圆心异侧时,如图②所示.
因为 AB=6?cm,CD=8?cm,
所以 AE=3?cm,CF=4?cm.
因为 OA=OC=5?cm,
所以 EO=4?cm,OF=3?cm,
所以 EF=OF+OE=7?cm.
故两条平行弦之间的距离为 7?cm 或 1?cm.
16. (1) 如图,过 A 作 BC 的垂线并延长交 DE 于点 F,
由于 △ABC 为等边三角形,则 AF 垂直平分 BC,
∵ 四边形 BDEC 为正方形,
∴ AF 也垂直平分 DE,
∴ 过点 A,D,E 三点的圆的圆心 O 在 AF 上,
连接 AD,OD,则 OA=OD,
∴ ∠OAD=∠ODA.
又 BC=BD=BA,
∴ ∠BAD=∠BDA.
而 AF∥BD,
∴ ∠DAO=∠BDA,
∴ ∠BAD=∠ADO,
∴ AB∥OD,
∴ 四边形 ABDO 为菱形,
∴ AO=AB=2,即 ⊙O 的半径为 2.
??????(2) 相等.求法与(1)相同.
如图,过 A 作 BC 的垂线并延长交 DE 于点 G,
由于 △ABC 为等腰三角形,则 AG 垂直平分 BC,
∵ 四边形 BDEC 为矩形,
∴ AG 也垂直平分 DE,
∴ 过点 A,D,E 三点的圆的圆心 O 在 AG 上,
连接 AD,OD,则 OA=OD,
∴ ∠OAD=∠ODA.
又 AB=AC=BD=2,
∴ ∠BAD=∠BDA.
而 AG∥BD,
∴ ∠DAO=∠BDA,
∴ ∠BAD=∠ADO,
∴ AB∥OD,
∴ 四边形 ABDO 为菱形,
∴ AO=AB=2,即 ⊙O 的半径为 2.
一、选择题(共6小题;共30分)
1. 如图所示,在半径为 5?cm 的 ⊙ O 中,弦 AB=6?cm,OC⊥AB 于点 C,则 OC 等于 ??
A. 3?cm B. 4?cm C. 5?cm D. 6?cm
2. 在 ⊙O 中,圆心 O 到弦 AB 的距离为 AB 长度的一半,则弦 AB 所对圆心角的大小为 ??
A. 30? B. 45? C. 60? D. 90?
3. 如图,在 ⊙O 中,AB,AC 是互相垂直且相等的两条弦,OD⊥AB,OE⊥AC,垂足分别为 D 、 E,若 AC=2?cm,则 ⊙O 的半径为 ??
A. 2?cm B. 2?cm C. 4?cm D. 5?cm
4. 已知点 P 是 ⊙O 内一点,⊙O 的半径为 5,OP=3,在过点 P 的所有 ⊙O 的弦中,弦长为整数的弦的条数为 ??
A. 2 B. 3 C. 4 D. 5
5. 下列说法中,正确的是 ??
A. 平分一条直径的弦必垂直于这条直径
B. 平分一条弧的直线垂直于这条弧所对的弦
C. 弦的垂线必经过这条弦所在圆的圆心
D. 在一个圆内平分一条弧同时平分它所对的弦的直线必经过这个圆的圆心
6. 如图,已知 ⊙O 的半径为 10,弦 AB=12,M 是 AB 上任意一点,则线段 OM 的长可能是 ??
A. 5 B. 7 C. 9 D. 11
二、填空题(共6小题;共30分)
7. 如图,在平面直角坐标系中,点 A0,1 、 B0,-1,以点 A 为圆心,AB 为半径作圆,交 x 轴于点 C 、 D,则 CD 的长是 ?.
8. 如图,AB 为圆 O 的直径,BC 为圆 O 的一条弦,过 O 点作 BC 的垂线,交 BC 于 D 点.若 AB=16,BC=12,则 △OBD 的面积为 ?.
9. 如图,AB 是 ⊙O 的直径,CD 为弦,CD⊥AB 于 E,若 CD=6,BE=1,则 ⊙O 的直径为 ?.
10. 如图,AB 是 ⊙O 的直径,CD 是 ⊙O 的一条弦,且 CD⊥AB 于点 E,CD=42,AE=2,则 ⊙O 的半径为 ?.
11. 如图,AB,CD 是半径为 5 的 ⊙O 的两条弦,AB=8,CD=6,MN 是直径,AB⊥MN 于点 E,CD⊥MN 于点 F,P 为 EF 上的任意一点,则 PA+PC 的最小值为 ?.
12. 如图,以 P-4.5,0 为圆心的 ⊙P 经过 -2,0 以 1 个单位/秒的速度沿 x 轴向右运动,则当 ⊙P 与 y 轴相交的弦长为 4 时,移动的时间为 ?.
三、解答题(共4小题;共60分)
13. 如图,一条公路的转弯处是一段圆弧 AB,点 O 是这段弧的圆心,AB=300?m,C 是 AB 上一点,OC⊥AB,垂足为 D,CD=45?m,求这段公路的半径.
14. 如图是一个半圆形桥洞截面示意图,圆心为 O,直径 AB 是河底线,弦 CD 是水位线,CD∥AB,且 AB=26?m,OE⊥CD 于点 E,水位正常时测得 OE:CD=5:24.
(1)求 CD 的长;
(2)现汛期来临,水面要以每小时 4?m 的速度上升,则经过多长时间桥洞会刚刚被灌满?
15. 在半径为 5?cm 的圆内有两条平行弦,一条弦长为 6?cm,另一条弦长为 8?cm,求两条平行弦之间的距离.
16. (1)如图 ①,多边形 ABDEC 是由边长为 2 的等边 △ABC 和正方形 BDEC 组成,⊙O 过 A,D,E 三点,求 ⊙O 的半径;
(2)如图②,若多边形 ABDEC 是由一个等腰三角形和一个矩形组成,AB=AC=BD=2,⊙O 过 A,D,E 三点,则 ⊙O 的半径与(1)中所求半径是否相等?
答案
第一部分
1. B
2. D
3. B
4. C
5. D
6. C
第二部分
7. 23
8. 67
【解析】∵OD⊥BC,
∴BD=CD=12BC=12×12=6.
在 Rt△BOD 中,
∵OB=12AB=8,BD=6,
∴OD=OB2-BD2=27,
∴S△OBD=12OD?BD=12×27×6=67.
9. 10
10. 3
【解析】∵ AB 是 ⊙O 的直径,且 CD⊥AB 于点 E,
∴ CE=12CD=12×42=22.
在 Rt△OCE 中,OC2=CE2+OE2,
设 ⊙O 的半径为 r,则 OC=r,OE=OA-AE=r-2,
∴ r2=222+r-22,解得 r=3,
∴ ⊙O 的半径为 3.
11. 72
【解析】连接 OA,OB,OC,作 CH⊥AB 于点 H,连接 BC 与 MN 交于点 P?,则当点 P 在点 P? 的位置时,PA+PC 最小,为 BC 的长.
根据垂径定理,得到 BE=12AB=4,CF=12CD=3,
∴OE=OB2-BE2=52-42=3,OF=OC2-CF2=52-32=4,
∴CH=OE+OF=3+4=7,BH=BE+EH=BE+CF=4+3=7,在 Rt△BCH 中,根据勾股定理得到 BC=72,则 PA+PC 的最小值为 72.
12. 3 秒或 6 秒
【解析】因为以 P-4.5,0 为圆心的 ⊙P 经过 -2,0,
所以 ⊙P 的半径为 2.5.
如图,
因为 AB=4,PE⊥AB,
所以 AE=12AB=2,
所以 PE=PA2-AE2=1.5,同理,PF=1.5,
所以点 E 的坐标为 -3,0,点 F 的坐标为 -6,0,
所以 ⊙P 以 1 个单位/秒的速度沿 x 轴向右运动,则当 ⊙P 与 y 轴相交的弦长为 4 时,则移动的时间为 3 秒或 6 秒.
第三部分
13. 设半径为 r?m,则 OD=r-CD=r-45,
∵OC⊥AB,
∴AD=BD=12AB=150m,
∴ 在 Rt△AOD 中,AO2=AD2+OD2,
即 r2=1502+r-452=22500+r2-90r+2025,
即 90r=24525,解得 r=272.5.
故这段公路的半径是 272.5?m.
14. (1) ∵ 直径 AB=26?m,
∴ OB=12AB=12×26=13m.
∵ OE⊥CD,
∴ DE=12CD.
∵ OE:CD=5:24,
∴ OE:ED=5:12,
设 OE=5x?m,则 ED=12x?m,
∴ 在 Rt△ODE 中,5x2+12x2=132,
解得 x=1,
∴ CD=2DE=2×12×1=24m.
??????(2) 由(1)得 OE=1×5=5m.
延长 OE 交圆 O 于点 F,
∴ EF=OF-OE=13-5=8m.
∴ 84=2小时,即经过 2 小时桥洞会刚刚被灌满.
15. 由题意构造图形,如图,弦 AB=6?cm,弦 CD=8?cm,过圆心 O 作 OE⊥AB 于点 E,且交 CD 于点 F.
因为 AB∥CD,
所以 OF⊥CD,
所以 EF 即为两条平行弦之间的距离.
①当弦 AB 和 CD 在圆心同侧时,如图①所示.
因为 AB=6?cm,CD=8?cm,
所以 AE=3?cm,CF=4?cm.
因为 OA=OC=5?cm,
所以 EO=4?cm,OF=3?cm,
所以 EF=OE-OF=1?cm.
②当弦 AB 和 CD 在圆心异侧时,如图②所示.
因为 AB=6?cm,CD=8?cm,
所以 AE=3?cm,CF=4?cm.
因为 OA=OC=5?cm,
所以 EO=4?cm,OF=3?cm,
所以 EF=OF+OE=7?cm.
故两条平行弦之间的距离为 7?cm 或 1?cm.
16. (1) 如图,过 A 作 BC 的垂线并延长交 DE 于点 F,
由于 △ABC 为等边三角形,则 AF 垂直平分 BC,
∵ 四边形 BDEC 为正方形,
∴ AF 也垂直平分 DE,
∴ 过点 A,D,E 三点的圆的圆心 O 在 AF 上,
连接 AD,OD,则 OA=OD,
∴ ∠OAD=∠ODA.
又 BC=BD=BA,
∴ ∠BAD=∠BDA.
而 AF∥BD,
∴ ∠DAO=∠BDA,
∴ ∠BAD=∠ADO,
∴ AB∥OD,
∴ 四边形 ABDO 为菱形,
∴ AO=AB=2,即 ⊙O 的半径为 2.
??????(2) 相等.求法与(1)相同.
如图,过 A 作 BC 的垂线并延长交 DE 于点 G,
由于 △ABC 为等腰三角形,则 AG 垂直平分 BC,
∵ 四边形 BDEC 为矩形,
∴ AG 也垂直平分 DE,
∴ 过点 A,D,E 三点的圆的圆心 O 在 AG 上,
连接 AD,OD,则 OA=OD,
∴ ∠OAD=∠ODA.
又 AB=AC=BD=2,
∴ ∠BAD=∠BDA.
而 AG∥BD,
∴ ∠DAO=∠BDA,
∴ ∠BAD=∠ADO,
∴ AB∥OD,
∴ 四边形 ABDO 为菱形,
∴ AO=AB=2,即 ⊙O 的半径为 2.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
