27.1 图形的相似 课件(共22张PPT)
文档属性
| 名称 | 27.1 图形的相似 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览






文档简介
27.1 图形的相似
1、通过具体实例理解图形相似的概念。
2、理解相似多边形和相似比的概念。
3、经历认识图形的过程,养成学生观察、比较、归纳总结的能力。
重点
理解相似图形概念。
难点
根据多边形相似进行相关计算。
学习目标
实例一:两个正方体纸盒
实例二:两个地球仪
观察这两组实例,你发现它们有什么相同点和不同点?
形状相同,大小不同
情境导入
实例三:应县木塔和模型
实例四:F22猛禽和模型
观察这两组实例,你发现它们有什么相同点和不同点?
形状相同,大小不同
情境导入
相似
相似图形的概念:
我们把形状相同的图形叫做相似图形。
全等形的概念:
能够完全重合的两个图形叫做全等形。
全等形和相似图形有什么关系呢?
相似图形
全等形
全等形是相似图形的一种特殊形式
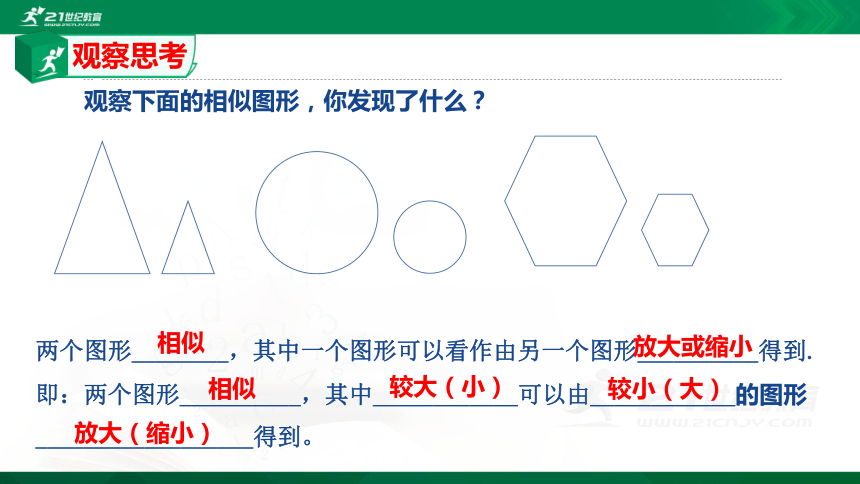
观察下面的相似图形,你发现了什么?
两个图形________,其中一个图形可以看作由另一个图形__________得到.
即:两个图形__________,其中____________可以由____________的图形
__________________得到。
放大或缩小
相似
相似
较大(小)
较小(大)
放大(缩小)
观察思考
你见过哈哈镜吗?哈哈镜与平面镜中的形象哪一个与你本人相似?请说明原因?
相似
因为相似图形的形状相同,而哈哈镜的原理是曲面镜引起的不规则光线反射与聚焦,做成散乱的影像。镜面扭曲的情况不同,成像的效果也会相异。所以哈哈镜中的人像是扭曲的,即哈哈镜所成像与本人不相似。
概念理解
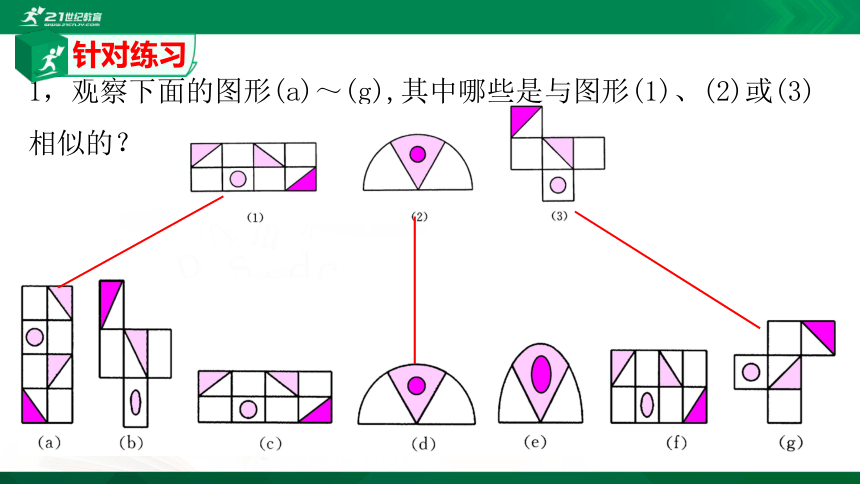
1,观察下面的图形(a)~(g),其中哪些是与图形(1)、(2)或(3) 相似的?
针对练习
2.下列图形不是相似图形的是( )
A.同一张底片冲洗出来的两张大小不同的照片,
B.用放大镜将一个细小物体图案放大,原有图案和放大图案,
C.某人的侧身照片和正面照片,
D.大小不同的两张中国地图,
C
(投影仪)
观察这两个五边形,你发现了什么?
相似
想一想这两个相似图形的边和角有什么关系呢?依据呢?
对应角相等、对应边成比例
两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到。
情境导入
相似多边形的概念
相似多边形概念:
相似多边形特征:
若两个边数相同的多边形,它们的对应角相等、对应边成比例,则这两个多边形叫做相似多边形。
对应角相等、对应边成比例
A
E
D
C
B
A’
B’
C’
D’
E’
若下面两个五边形相似,你知道它们的角和边有什么关系?
∠A=∠A’, ∠B=∠B’, ∠C=∠C’, ∠D=∠D’, ∠E=∠E’
ABA′B′= BCB′C′= CDC′D′= DED′E′= AEA′E′
?
相似比概念:
相似多边形对应边的比
思考
已知四条线段长度(a≠0)如下图,这四条线段长度成比例吗?
a
1.5a
2a
3a
线段一
线段二
线段三
线段四
提示:如果有四条线段a、b、c、d,如果两条线段的长度比与另外两条的长度比相等,如????????=????????(或ad=cb),我们就说这四条线段成比例。
?
∵线段一线段三=线段二线段四 =????????
?
∴四条线段长度成比例
1)任意两个等边三角形相似吗?
2)任意两个正方形相似吗?
3)任意两个正五边形相似吗?
4)任意两个正n边形相似吗?
任意两个边数相等的正多边形都相似.
观察思考
如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度 x.
.
1)解:∵ 四边形 ABCD 和 EFGH 相似
∴ 它们的对应角相等.由此可得
∴∠α=∠C=83°,∠A=∠E=118°
在四边形ABCD中,
∠β=360°- ∠A - ∠B - ∠C=81°
2)∵ 四边形ABCD和EFGH相似,
∴ 它们的对应边成比例
∴ ????????????????=????????????????得????????????=????????????????,解得 x=28
?
针对练习
1.下列说法中,正确的是( )
A.所有的等腰三角形都相似
B.所有的菱形都相似
C.所有的矩形都相似
D.所有的等腰直角三角形都相似
【详解】
A、所有的等腰三角形,边的比不一定相等,对应角不一定对应相等,故错误;
B、所有的菱形,边的比一定相等,而对应角不一定对应相等,故错误;
C、所有的矩形,对应角的度数一定相同,但对应边的比值不一定相等,故错误;
D、所有的等腰直角三角形,边的比一定相等,而对应角对应相等,故正确.
故选:D.
课堂练习
2.下列结论中,错误的有:( )
①所有的菱形都相似; ②放大镜下的图形与原图形不一定相似;
③等边三角形都相似; ④有一个角为110度的两个等腰三角形相似;
⑤所有的矩形不一定相似.
A.1个 B.2个 C.3个 D.4个
【详解】
相似多边形对应边成比例,对应角相等,菱形之间的对应角不一定相等,故①错误;
放大镜下的图形只是大小发生了变化,形状不变,所以一定相似,②错误;
等边三角形的角都是60°,一定相似,③正确;
钝角只能是等腰三角形的顶角,则底角只能是35°,所以两个等腰三角形相似,④正确;
矩形之间的对应角相等,但是对应边不一定成比例,故⑤正确.
有2个错误,故选B.
3.下列各组线段的长度成比例的是( )
A.6cm、2cm、1cm、4cm B.4cm、5cm、6cm、7cm
C.3cm、4cm、5cm、6cm D.6cm、3cm、8cm、4cm
4.在比例尺是1:4000的安庆市城区地图上,菱湖南路的长度约为25????????,它的实际长度约为( )
A.160???????? B.160???? C.1000???????? D.1000????
?
【详解】解:设它的实际长度为xcm,根据题意得: ????????????????????=?????????????,
解得:x=100000,
∵100000cm=1000m,∴它的实际长度为1000m.故选:D.
?
5.如图所示,在长为8 cm,宽为4 cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是( )
A.2 cm2 B.4 cm2 C.8 cm2 D.16 cm2
【解析】
设留下矩形的宽为xcm,
∵留下的矩形(图中阴影部分)与原矩形相似,
∴????4=48,
解得????=2
则留下矩形的面积为2×4=8(????????2) .故选C.
?
1.本节课学习了哪些内容?
3.相似多边形的性质是什么?
2.什么是相似多边形?“两个相似多边形”需满足什么条件?
课堂小结
相似多边形的性质:
相似多边形的对应角相等,对应边成比例.
∵
课堂小结
多边形的判定:
(定义)
∵
课堂小结
谢谢!
1、通过具体实例理解图形相似的概念。
2、理解相似多边形和相似比的概念。
3、经历认识图形的过程,养成学生观察、比较、归纳总结的能力。
重点
理解相似图形概念。
难点
根据多边形相似进行相关计算。
学习目标
实例一:两个正方体纸盒
实例二:两个地球仪
观察这两组实例,你发现它们有什么相同点和不同点?
形状相同,大小不同
情境导入
实例三:应县木塔和模型
实例四:F22猛禽和模型
观察这两组实例,你发现它们有什么相同点和不同点?
形状相同,大小不同
情境导入
相似
相似图形的概念:
我们把形状相同的图形叫做相似图形。
全等形的概念:
能够完全重合的两个图形叫做全等形。
全等形和相似图形有什么关系呢?
相似图形
全等形
全等形是相似图形的一种特殊形式
观察下面的相似图形,你发现了什么?
两个图形________,其中一个图形可以看作由另一个图形__________得到.
即:两个图形__________,其中____________可以由____________的图形
__________________得到。
放大或缩小
相似
相似
较大(小)
较小(大)
放大(缩小)
观察思考
你见过哈哈镜吗?哈哈镜与平面镜中的形象哪一个与你本人相似?请说明原因?
相似
因为相似图形的形状相同,而哈哈镜的原理是曲面镜引起的不规则光线反射与聚焦,做成散乱的影像。镜面扭曲的情况不同,成像的效果也会相异。所以哈哈镜中的人像是扭曲的,即哈哈镜所成像与本人不相似。
概念理解
1,观察下面的图形(a)~(g),其中哪些是与图形(1)、(2)或(3) 相似的?
针对练习
2.下列图形不是相似图形的是( )
A.同一张底片冲洗出来的两张大小不同的照片,
B.用放大镜将一个细小物体图案放大,原有图案和放大图案,
C.某人的侧身照片和正面照片,
D.大小不同的两张中国地图,
C
(投影仪)
观察这两个五边形,你发现了什么?
相似
想一想这两个相似图形的边和角有什么关系呢?依据呢?
对应角相等、对应边成比例
两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到。
情境导入
相似多边形的概念
相似多边形概念:
相似多边形特征:
若两个边数相同的多边形,它们的对应角相等、对应边成比例,则这两个多边形叫做相似多边形。
对应角相等、对应边成比例
A
E
D
C
B
A’
B’
C’
D’
E’
若下面两个五边形相似,你知道它们的角和边有什么关系?
∠A=∠A’, ∠B=∠B’, ∠C=∠C’, ∠D=∠D’, ∠E=∠E’
ABA′B′= BCB′C′= CDC′D′= DED′E′= AEA′E′
?
相似比概念:
相似多边形对应边的比
思考
已知四条线段长度(a≠0)如下图,这四条线段长度成比例吗?
a
1.5a
2a
3a
线段一
线段二
线段三
线段四
提示:如果有四条线段a、b、c、d,如果两条线段的长度比与另外两条的长度比相等,如????????=????????(或ad=cb),我们就说这四条线段成比例。
?
∵线段一线段三=线段二线段四 =????????
?
∴四条线段长度成比例
1)任意两个等边三角形相似吗?
2)任意两个正方形相似吗?
3)任意两个正五边形相似吗?
4)任意两个正n边形相似吗?
任意两个边数相等的正多边形都相似.
观察思考
如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度 x.
.
1)解:∵ 四边形 ABCD 和 EFGH 相似
∴ 它们的对应角相等.由此可得
∴∠α=∠C=83°,∠A=∠E=118°
在四边形ABCD中,
∠β=360°- ∠A - ∠B - ∠C=81°
2)∵ 四边形ABCD和EFGH相似,
∴ 它们的对应边成比例
∴ ????????????????=????????????????得????????????=????????????????,解得 x=28
?
针对练习
1.下列说法中,正确的是( )
A.所有的等腰三角形都相似
B.所有的菱形都相似
C.所有的矩形都相似
D.所有的等腰直角三角形都相似
【详解】
A、所有的等腰三角形,边的比不一定相等,对应角不一定对应相等,故错误;
B、所有的菱形,边的比一定相等,而对应角不一定对应相等,故错误;
C、所有的矩形,对应角的度数一定相同,但对应边的比值不一定相等,故错误;
D、所有的等腰直角三角形,边的比一定相等,而对应角对应相等,故正确.
故选:D.
课堂练习
2.下列结论中,错误的有:( )
①所有的菱形都相似; ②放大镜下的图形与原图形不一定相似;
③等边三角形都相似; ④有一个角为110度的两个等腰三角形相似;
⑤所有的矩形不一定相似.
A.1个 B.2个 C.3个 D.4个
【详解】
相似多边形对应边成比例,对应角相等,菱形之间的对应角不一定相等,故①错误;
放大镜下的图形只是大小发生了变化,形状不变,所以一定相似,②错误;
等边三角形的角都是60°,一定相似,③正确;
钝角只能是等腰三角形的顶角,则底角只能是35°,所以两个等腰三角形相似,④正确;
矩形之间的对应角相等,但是对应边不一定成比例,故⑤正确.
有2个错误,故选B.
3.下列各组线段的长度成比例的是( )
A.6cm、2cm、1cm、4cm B.4cm、5cm、6cm、7cm
C.3cm、4cm、5cm、6cm D.6cm、3cm、8cm、4cm
4.在比例尺是1:4000的安庆市城区地图上,菱湖南路的长度约为25????????,它的实际长度约为( )
A.160???????? B.160???? C.1000???????? D.1000????
?
【详解】解:设它的实际长度为xcm,根据题意得: ????????????????????=?????????????,
解得:x=100000,
∵100000cm=1000m,∴它的实际长度为1000m.故选:D.
?
5.如图所示,在长为8 cm,宽为4 cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是( )
A.2 cm2 B.4 cm2 C.8 cm2 D.16 cm2
【解析】
设留下矩形的宽为xcm,
∵留下的矩形(图中阴影部分)与原矩形相似,
∴????4=48,
解得????=2
则留下矩形的面积为2×4=8(????????2) .故选C.
?
1.本节课学习了哪些内容?
3.相似多边形的性质是什么?
2.什么是相似多边形?“两个相似多边形”需满足什么条件?
课堂小结
相似多边形的性质:
相似多边形的对应角相等,对应边成比例.
∵
课堂小结
多边形的判定:
(定义)
∵
课堂小结
谢谢!
