2021年中考数学试题 第三章 函数 专题九 平面直角坐标系(word版含答案)
文档属性
| 名称 | 2021年中考数学试题 第三章 函数 专题九 平面直角坐标系(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 396.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览


文档简介
2021年中考数学试题
第三章
函数
专题九
平面直角坐标系
一、解答题(共3小题;共39分)
1.
有甲、乙两个均装有进水管与出水管的容器,初始时,两容器同时只开进水管,甲容器到
分钟时,关闭进水管而打开出水管;到
分钟时,又打开了进水管,此时既进水又出水;到
分钟时,同时关闭两容器的所有水管.两容器每分钟进水量与出水量均为常数,容器内的水量
(升)与时间
(分)之间的函数关系如图所示,解答下列问题:
(1)甲容器的进水管每分钟进水
?
升,出水管每分钟出水
?
升;
(2)求乙容器内的水量
关于时间
的函数表达式;
(3)求从初始时刻到两容器最后一次水量相等时所需要的时间.
2.
年
月
日,以“天人长安,创意自然——城市与自然和谐共生”为主题的世界园艺博览会在西安隆重开园.这次世园会的门票分为个人票、团体票两大类,其中个人票设置有三种:
某社区居委会为奖励“和谐家庭”,欲购买个人票
张,其中B种票张数是A种票张数的
倍还多
张.设需购A种票张数为
,C种票张数为
.
(1)写出
与
之间的函数关系式.
(2)设购票总费用为
元,求出
(元)与
(张)之间的函数关系式.
(3)若每种票至少购买
张,其中购买A种票不少于
张,则共有几种购票方案?并求出购票总费用最少时,购买A,B,C三种票的张数.
3.
某商场经营某种品牌的童装,购进时的单价是
元.根据市场调查,在一段时间内,销售单价是
元时,销售量是
件,而销售单价每降低
元,就可多售出
件.
(1)写出销售量
(件)与销售单价
(元)之间的函数关系式;
(2)写出销售该品牌童装获得的利润
(元)与销售单价
(元)之间的函数关系式;
(3)若童装厂规定该品牌童装销售单价不低于
元,且商场要完成不少于
件的销售任务,则商场销售该品牌童装获得的最大利润是多少元?
二、选择题(共4小题;共20分)
4.
在平面直角坐标系中,把点
绕原点
顺时针旋转
,所得到的对应点
的坐标为
A.
B.
C.
D.
5.
若
轴上的点
到
轴的距离为
,则点
的坐标为
A.
B.
C.
或
D.
或
6.
如果点
在第四象限,则
的取值范围是
A.
B.
C.
D.
7.
若以
,,
三点为顶点画平行四边形,则第四个顶点不可能在
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
三、填空题(共3小题;共15分)
8.
若点
在第二象限,则点
在第
?象限.
9.
若点
到
轴的距离是
,到
轴的距离是
,那么
点坐标可以是
?(写出一个即可).
10.
已知点
的坐标
,且点
到两坐标轴的距离相等,则点
的坐标是
?.
四、选择题(共5小题;共25分)
11.
在平面直角坐标系中,点
关于
轴的对称点的坐标是
A.
B.
C.
D.
12.
在平面直角坐标系中,将点
向上平移
个单位长度,再向左平移
个单位长度,得到点
,则点
的坐标是
A.
B.
C.
D.
13.
已知点
坐标为
,点
坐标为
,若将线段
平移至
,使点
的对应点
的坐标为
,则点
的坐标为
A.
B.
C.
D.
14.
在平面直角坐标系中,点
的坐标为
,点
的坐标为
,则线段
的中点坐标为
A.
B.
C.
D.
15.
在平面直角坐标系中,点
,
的坐标如图所示,将
绕原点
顺时针方向旋转
得
,则点
的对应点
的坐标为
A.
B.
C.
D.
五、填空题(共2小题;共10分)
16.
在平面直角坐标系中,将点
向上平移
个单位,则平移后的点的坐标为
?.
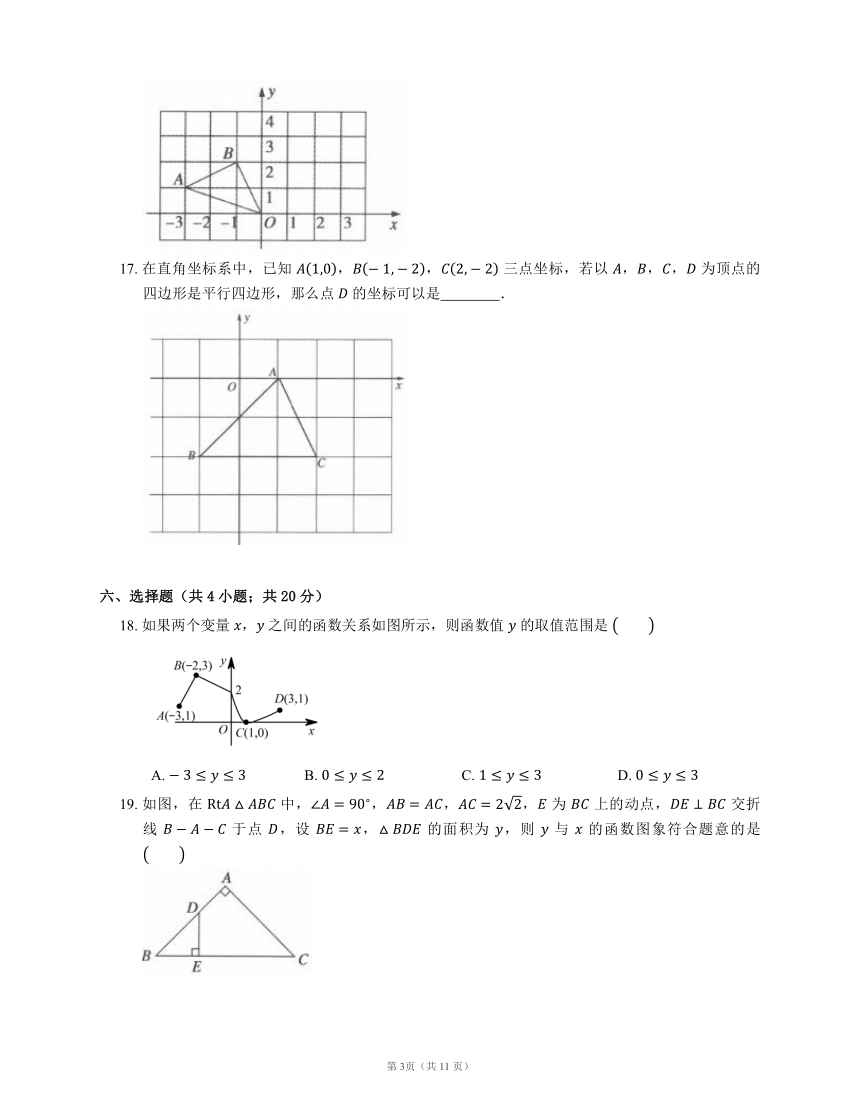
17.
在直角坐标系中,已知
,,
三点坐标,若以
,,,
为顶点的四边形是平行四边形,那么点
的坐标可以是
?.
六、选择题(共4小题;共20分)
18.
如果两个变量
,
之间的函数关系如图所示,则函数值
的取值范围是
A.
B.
C.
D.
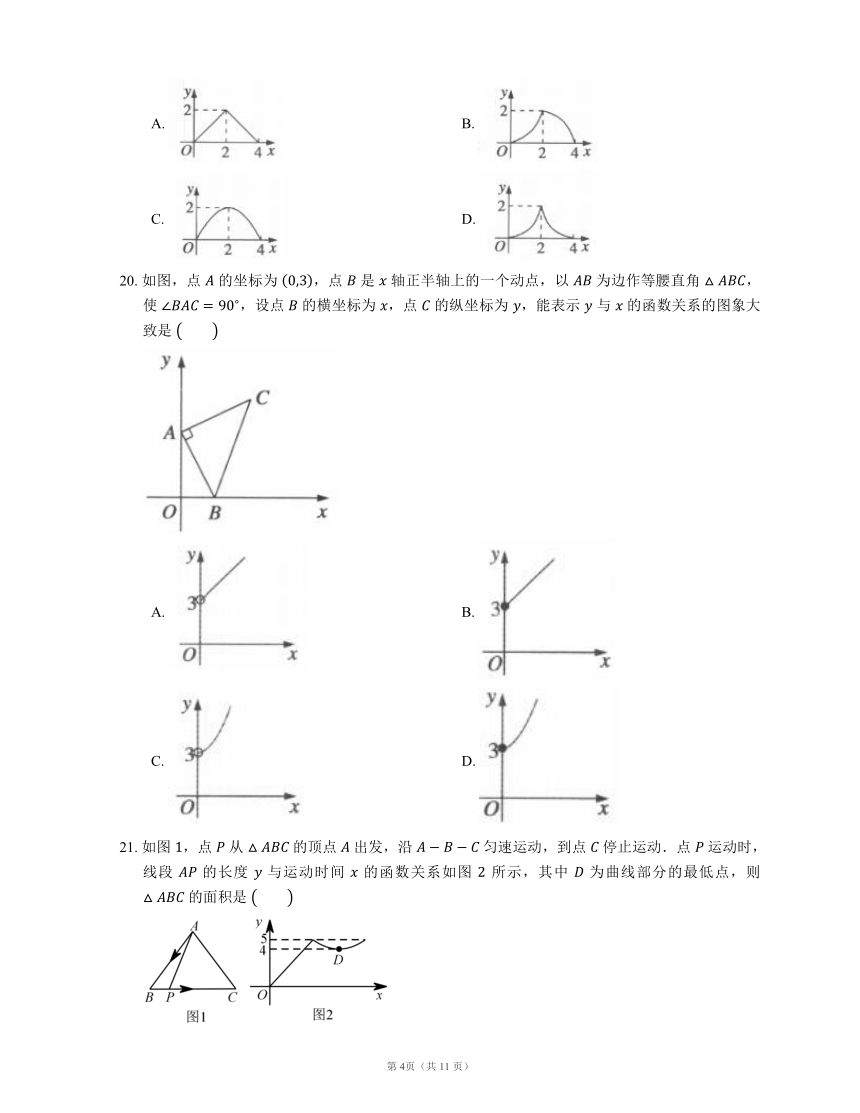
19.
如图,在
中,,,,
为
上的动点,
交折线
于点
,设
,
的面积为
,则
与
的函数图象符合题意的是
A.
B.
C.
D.
20.
如图,点
的坐标为
,点
是
轴正半轴上的一个动点,以
为边作等腰直角
,使
,设点
的横坐标为
,点
的纵坐标为
,能表示
与
的函数关系的图象大致是
A.
B.
C.
D.
21.
如图
,点
从
的顶点
出发,沿
匀速运动,到点
停止运动.点
运动时,线段
的长度
与运动时间
的函数关系如图
所示,其中
为曲线部分的最低点,则
的面积是
A.
B.
C.
D.
七、解答题(共1小题;共13分)
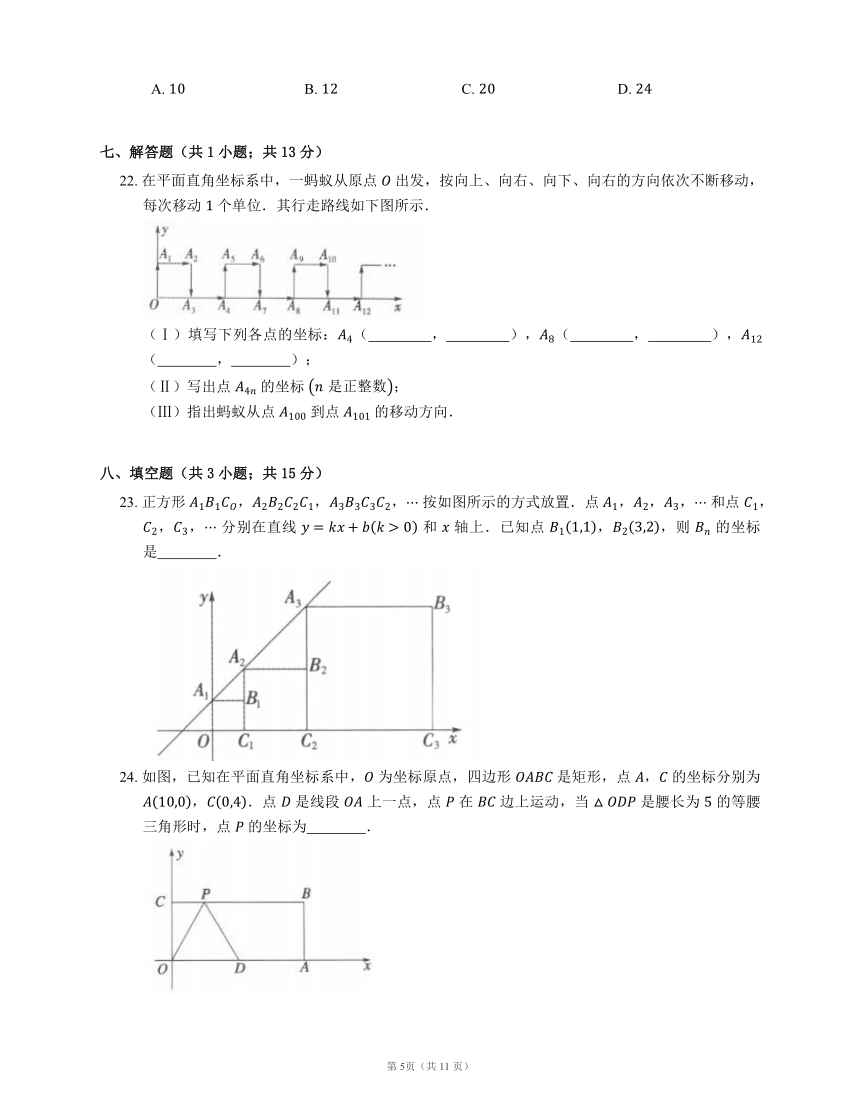
22.
在平面直角坐标系中,一蚂蚁从原点
出发,按向上、向右、向下、向右的方向依次不断移动,每次移动
个单位.其行走路线如下图所示.
(Ⅰ)填写下列各点的坐标:(
?,
?),(
?,
?),(
?,
?);
(Ⅱ)写出点
的坐标
;
(Ⅲ)指出蚂蚁从点
到点
的移动方向.
八、填空题(共3小题;共15分)
23.
正方形
,,,
按如图所示的方式放置.点
,,,
和点
,,,
分别在直线
和
轴上.已知点
,,则
的坐标是
?.
24.
如图,已知在平面直角坐标系中,
为坐标原点,四边形
是矩形,点
,
的坐标分别为
,.点
是线段
上一点,点
在
边上运动,当
是腰长为
的等腰三角形时,点
的坐标为
?.
25.
如图,在直角坐标系中,
是原点,已知
,
是坐标轴上的一点,若以
,,
三点组成的三角形为等腰三角形,则满足条件的点
共有
?个,写出其中两个点
的坐标是
?.
答案
第一部分
1.
(1)
;
????(2)
设
,
把
,
代入上式,得
解得
.
????(3)
,,
当
时,,
设
,
把
,
代入上式,得
解得
,
由题意,得
,解得
,
从初始时刻到两容器最后一次水量相等时需要
分钟.
2.
(1)
.
????(2)
.
????(3)
由题意,得
解得
.
是正整数,
可取
,,.
共有
种购票方案.
,
随着
的增大而减小,当
时,
的取值最小,
即当A种票购买
张时,购票的总费用最少.
购票总费用最少时,购买A,B,C三种票张数分别为
,,.
3.
(1)
由题意,得
.
????(2)
由题意,得
.
????(3)
由题意得
解得
.
对称轴为
.
又
,
当
时,
随
增大而减小,
当
时,.
答:商场销售该品牌童装获得的最大利润是
元.
第二部分
4.
D
【解析】根据题意得,点
关于原点的对称点是点
,
点的坐标为
,
点
的坐标为
.
5.
C
6.
A
7.
C
第三部分
8.
三
9.
或
或
或
(写出一个即可)
10.
或
第四部分
11.
A
12.
C
13.
A
【解析】因为将线段
平移至
,
点坐标由
变为
,即横坐标向右平移
个单位,纵坐标向上平移
个单位,
所以将
点坐标向右平移
个单位,向上平移
个单位得到
点坐标为
.
14.
A
【解析】,,
故线段
的中点坐标为
.
15.
D
第五部分
16.
17.
【解析】,,
写出其中一个即可.
第六部分
18.
D
19.
B
【解析】
在
中,,,,
,.
①当
时,
,,
的面积
,
函数图象为顶点在原点,开口向上的抛物线,故A,C错误;
②当
时,
,,
的面积
,
函数图象为开口向下的抛物线.故B正确,D错误.
20.
A
【解析】作
轴,作
于点
,如图所示,
由已知可知,,,,,,点
的纵坐标是
,
因为
轴,
所以
,
所以
,
所以
,
所以
,
在
和
中,
所以
(),
所以
,,
因为点
到
轴的距离为
,点
到
轴的距离等于点
到
的距离
,
所以
.
21.
B
【解析】根据图象可知,点
在
上运动时,此时
不断增大,
由图象可知:点
从
向
运动时,
的最大值为
,即
,
点
从
向
运动时,
的最小值为
,
即
边上的高为
,
当
,,
此时,由勾股定理可知:,
由于图象的曲线部分是轴对称图形,
,
,
的面积为:.
第七部分
22.
(I),,;
(Ⅱ)
的坐标为
;
(Ⅲ)蚂蚁从点
到点
的移动方向是向上.
第八部分
23.
【解析】由图得
,,将点
,
坐标代入直线
可得
,直线
与
轴交点为
,坐标为
,设
,
由
,
得
,
,,
.
同理:,
归纳
.
24.
或
或
【解析】①当
或
时,
为
;
②
时,
为
;
③当
靠近
,有
时,
为
.
25.
,
或
或
或
或
或
或
或
(答案不唯一,写出
个中的两个即可).
第1页(共1
页)
第三章
函数
专题九
平面直角坐标系
一、解答题(共3小题;共39分)
1.
有甲、乙两个均装有进水管与出水管的容器,初始时,两容器同时只开进水管,甲容器到
分钟时,关闭进水管而打开出水管;到
分钟时,又打开了进水管,此时既进水又出水;到
分钟时,同时关闭两容器的所有水管.两容器每分钟进水量与出水量均为常数,容器内的水量
(升)与时间
(分)之间的函数关系如图所示,解答下列问题:
(1)甲容器的进水管每分钟进水
?
升,出水管每分钟出水
?
升;
(2)求乙容器内的水量
关于时间
的函数表达式;
(3)求从初始时刻到两容器最后一次水量相等时所需要的时间.
2.
年
月
日,以“天人长安,创意自然——城市与自然和谐共生”为主题的世界园艺博览会在西安隆重开园.这次世园会的门票分为个人票、团体票两大类,其中个人票设置有三种:
某社区居委会为奖励“和谐家庭”,欲购买个人票
张,其中B种票张数是A种票张数的
倍还多
张.设需购A种票张数为
,C种票张数为
.
(1)写出
与
之间的函数关系式.
(2)设购票总费用为
元,求出
(元)与
(张)之间的函数关系式.
(3)若每种票至少购买
张,其中购买A种票不少于
张,则共有几种购票方案?并求出购票总费用最少时,购买A,B,C三种票的张数.
3.
某商场经营某种品牌的童装,购进时的单价是
元.根据市场调查,在一段时间内,销售单价是
元时,销售量是
件,而销售单价每降低
元,就可多售出
件.
(1)写出销售量
(件)与销售单价
(元)之间的函数关系式;
(2)写出销售该品牌童装获得的利润
(元)与销售单价
(元)之间的函数关系式;
(3)若童装厂规定该品牌童装销售单价不低于
元,且商场要完成不少于
件的销售任务,则商场销售该品牌童装获得的最大利润是多少元?
二、选择题(共4小题;共20分)
4.
在平面直角坐标系中,把点
绕原点
顺时针旋转
,所得到的对应点
的坐标为
A.
B.
C.
D.
5.
若
轴上的点
到
轴的距离为
,则点
的坐标为
A.
B.
C.
或
D.
或
6.
如果点
在第四象限,则
的取值范围是
A.
B.
C.
D.
7.
若以
,,
三点为顶点画平行四边形,则第四个顶点不可能在
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
三、填空题(共3小题;共15分)
8.
若点
在第二象限,则点
在第
?象限.
9.
若点
到
轴的距离是
,到
轴的距离是
,那么
点坐标可以是
?(写出一个即可).
10.
已知点
的坐标
,且点
到两坐标轴的距离相等,则点
的坐标是
?.
四、选择题(共5小题;共25分)
11.
在平面直角坐标系中,点
关于
轴的对称点的坐标是
A.
B.
C.
D.
12.
在平面直角坐标系中,将点
向上平移
个单位长度,再向左平移
个单位长度,得到点
,则点
的坐标是
A.
B.
C.
D.
13.
已知点
坐标为
,点
坐标为
,若将线段
平移至
,使点
的对应点
的坐标为
,则点
的坐标为
A.
B.
C.
D.
14.
在平面直角坐标系中,点
的坐标为
,点
的坐标为
,则线段
的中点坐标为
A.
B.
C.
D.
15.
在平面直角坐标系中,点
,
的坐标如图所示,将
绕原点
顺时针方向旋转
得
,则点
的对应点
的坐标为
A.
B.
C.
D.
五、填空题(共2小题;共10分)
16.
在平面直角坐标系中,将点
向上平移
个单位,则平移后的点的坐标为
?.
17.
在直角坐标系中,已知
,,
三点坐标,若以
,,,
为顶点的四边形是平行四边形,那么点
的坐标可以是
?.
六、选择题(共4小题;共20分)
18.
如果两个变量
,
之间的函数关系如图所示,则函数值
的取值范围是
A.
B.
C.
D.
19.
如图,在
中,,,,
为
上的动点,
交折线
于点
,设
,
的面积为
,则
与
的函数图象符合题意的是
A.
B.
C.
D.
20.
如图,点
的坐标为
,点
是
轴正半轴上的一个动点,以
为边作等腰直角
,使
,设点
的横坐标为
,点
的纵坐标为
,能表示
与
的函数关系的图象大致是
A.
B.
C.
D.
21.
如图
,点
从
的顶点
出发,沿
匀速运动,到点
停止运动.点
运动时,线段
的长度
与运动时间
的函数关系如图
所示,其中
为曲线部分的最低点,则
的面积是
A.
B.
C.
D.
七、解答题(共1小题;共13分)
22.
在平面直角坐标系中,一蚂蚁从原点
出发,按向上、向右、向下、向右的方向依次不断移动,每次移动
个单位.其行走路线如下图所示.
(Ⅰ)填写下列各点的坐标:(
?,
?),(
?,
?),(
?,
?);
(Ⅱ)写出点
的坐标
;
(Ⅲ)指出蚂蚁从点
到点
的移动方向.
八、填空题(共3小题;共15分)
23.
正方形
,,,
按如图所示的方式放置.点
,,,
和点
,,,
分别在直线
和
轴上.已知点
,,则
的坐标是
?.
24.
如图,已知在平面直角坐标系中,
为坐标原点,四边形
是矩形,点
,
的坐标分别为
,.点
是线段
上一点,点
在
边上运动,当
是腰长为
的等腰三角形时,点
的坐标为
?.
25.
如图,在直角坐标系中,
是原点,已知
,
是坐标轴上的一点,若以
,,
三点组成的三角形为等腰三角形,则满足条件的点
共有
?个,写出其中两个点
的坐标是
?.
答案
第一部分
1.
(1)
;
????(2)
设
,
把
,
代入上式,得
解得
.
????(3)
,,
当
时,,
设
,
把
,
代入上式,得
解得
,
由题意,得
,解得
,
从初始时刻到两容器最后一次水量相等时需要
分钟.
2.
(1)
.
????(2)
.
????(3)
由题意,得
解得
.
是正整数,
可取
,,.
共有
种购票方案.
,
随着
的增大而减小,当
时,
的取值最小,
即当A种票购买
张时,购票的总费用最少.
购票总费用最少时,购买A,B,C三种票张数分别为
,,.
3.
(1)
由题意,得
.
????(2)
由题意,得
.
????(3)
由题意得
解得
.
对称轴为
.
又
,
当
时,
随
增大而减小,
当
时,.
答:商场销售该品牌童装获得的最大利润是
元.
第二部分
4.
D
【解析】根据题意得,点
关于原点的对称点是点
,
点的坐标为
,
点
的坐标为
.
5.
C
6.
A
7.
C
第三部分
8.
三
9.
或
或
或
(写出一个即可)
10.
或
第四部分
11.
A
12.
C
13.
A
【解析】因为将线段
平移至
,
点坐标由
变为
,即横坐标向右平移
个单位,纵坐标向上平移
个单位,
所以将
点坐标向右平移
个单位,向上平移
个单位得到
点坐标为
.
14.
A
【解析】,,
故线段
的中点坐标为
.
15.
D
第五部分
16.
17.
【解析】,,
写出其中一个即可.
第六部分
18.
D
19.
B
【解析】
在
中,,,,
,.
①当
时,
,,
的面积
,
函数图象为顶点在原点,开口向上的抛物线,故A,C错误;
②当
时,
,,
的面积
,
函数图象为开口向下的抛物线.故B正确,D错误.
20.
A
【解析】作
轴,作
于点
,如图所示,
由已知可知,,,,,,点
的纵坐标是
,
因为
轴,
所以
,
所以
,
所以
,
所以
,
在
和
中,
所以
(),
所以
,,
因为点
到
轴的距离为
,点
到
轴的距离等于点
到
的距离
,
所以
.
21.
B
【解析】根据图象可知,点
在
上运动时,此时
不断增大,
由图象可知:点
从
向
运动时,
的最大值为
,即
,
点
从
向
运动时,
的最小值为
,
即
边上的高为
,
当
,,
此时,由勾股定理可知:,
由于图象的曲线部分是轴对称图形,
,
,
的面积为:.
第七部分
22.
(I),,;
(Ⅱ)
的坐标为
;
(Ⅲ)蚂蚁从点
到点
的移动方向是向上.
第八部分
23.
【解析】由图得
,,将点
,
坐标代入直线
可得
,直线
与
轴交点为
,坐标为
,设
,
由
,
得
,
,,
.
同理:,
归纳
.
24.
或
或
【解析】①当
或
时,
为
;
②
时,
为
;
③当
靠近
,有
时,
为
.
25.
,
或
或
或
或
或
或
或
(答案不唯一,写出
个中的两个即可).
第1页(共1
页)
同课章节目录
