沪科版数学八年级下册19.2三角形的中位线中考题汇编(Word版 含答案)
文档属性
| 名称 | 沪科版数学八年级下册19.2三角形的中位线中考题汇编(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 54.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 00:00:00 | ||
图片预览

文档简介
沪科版数学八年级三角形的中位线中考题汇编
1
一、
选择题
1.
(2019·盐城)如图,D,E分别是△ABC的边BA,BC的中点,AC=3,则DE的长为( )
A.
2
B.
C.
3
D.
2.
(2019·娄底)顺次连接菱形四边中点得到的四边形是( )
A.
平行四边形
B.
菱形
C.
矩形
D.
正方形
3.
(2019·铜仁)如图,D是△ABC内的一点,BD⊥CD,AD=7,BD=4,CD=3,E,F,G,H分别是AB,BD,CD,AC的中点,则四边形EFGH的周长为( )
A.
12
B.
14
C.
24
D.
21
4.
(2018·达州)如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M.若BC=7,则MN的长为( )
A.
B.
2
C.
D.
3
二、
填空题
5.
(2019·长沙)如图,要测量池塘两岸相对的A,B两点间的距离,可以在池塘外选一点C,连接AC,BC,分别取AC,BC的中点D,E,测得DE=50
m,则AB的长是________m.
6.
(2019·梧州)如图,在△ABC中,D,E分别是AB,AC的中点,F,G分别是AD,AE的中点,且FG=2
cm,则BC的长度是________cm.
7.
(2019·泰安)如图,在矩形ABCD中,AB=4,AD=2,E为AB的中点,F为EC上一动点,P为DF中点,连接PB,则PB的最小值是________.
三、
解答题
8.
(2019·徐州)如图,在矩形ABCD中,AC,BD交于点O,M,N分别为BC,OC的中点.若MN=4,求AC的长.
第8题
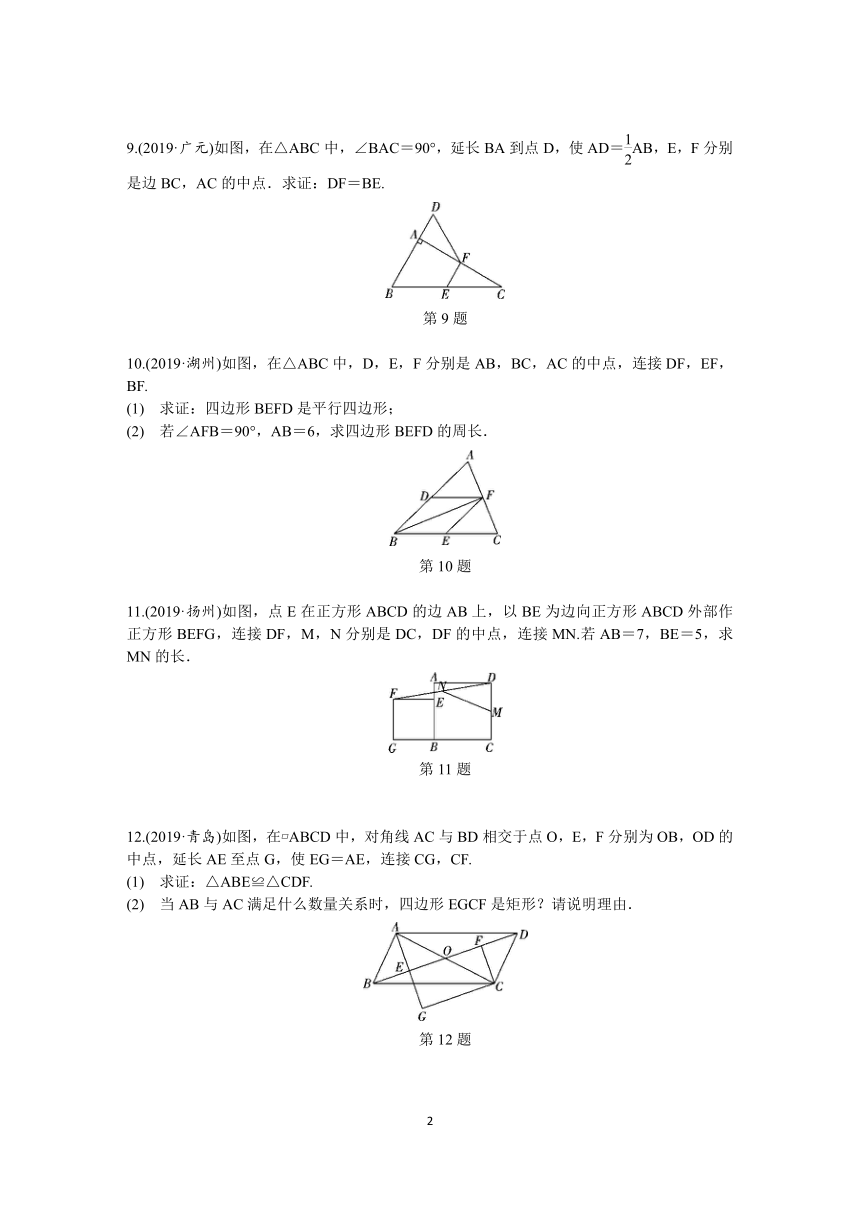
9.(2019·广元)如图,在△ABC中,∠BAC=90°,延长BA到点D,使AD=AB,E,F分别是边BC,AC的中点.求证:DF=BE.
第9题
10.(2019·湖州)如图,在△ABC中,D,E,F分别是AB,BC,AC的中点,连接DF,EF,BF.
(1)
求证:四边形BEFD是平行四边形;
(2)
若∠AFB=90°,AB=6,求四边形BEFD的周长.
第10题
11.(2019·扬州)如图,点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M,N分别是DC,DF的中点,连接MN.若AB=7,BE=5,求MN的长.
第11题
12.(2019·青岛)如图,在?ABCD中,对角线AC与BD相交于点O,E,F分别为OB,OD的中点,延长AE至点G,使EG=AE,连接CG,CF.
(1)
求证:△ABE≌△CDF.
(2)
当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.
第12题
13.(2019·淄博)如图,正方形ABDE和正方形BCFG的边AB,BC在同一条直线上,且AB=2BC,取EF的中点M.连接MD,MG,MB.求证:DM⊥MG,并求的值.
参考答案
一、
D
C
A
C
二、
100
8
2
三、
∵
M,N分别为BC,OC的中点,∴
BO=2MN=8.∵
四边形ABCD是矩形,∴
AC=BD=2BO=16
连接AE.∵
E,F分别是边BC,AC的中点,∴
EF∥AB,EF=AB.∵
AD=AB,∴
EF=AD.又∵
EF∥AD,∴
四边形ADFE是平行四边形.∴
DF=AE.∵
在Rt△ABC中,E是BC的中点,∴
AE=BC=BE=CE.∴
DF=BE
(1)
∵
D,E,F分别是AB,BC,AC的中点,∴
EF∥AB,DF∥BC.∴
四边形BEFD是平行四边形 (2)
∵
∠AFB=90°,D是AB的中点,∴
DF=DB=AB=3.∴
四边形BEFD是菱形.∴
BE=EF=DF=DB=3.∴
四边形BEFD的周长为4×3=12
如图,连接CF.∵
四边形ABCD和四边形BEFG都是正方形,∴
GF=GB=BE=5,BC=AB=7,∠G=90°.∴
GC=GB+BC=5+7=12.∴
CF===13.∵
M,N分别是DC,DF的中点,∴
MN=CF=
(1)
∵
四边形ABCD是平行四边形,∴
AB=CD,AB∥CD,OB=OD,OA=OC.∴
∠ABE=∠CDF.∵
E,F分别为OB,OD的中点,∴
BE=OB,DF=OD.∴
BE=DF.在△ABE和△CDF中,∴
△ABE≌△CDF (2)
当AC=2AB时,四边形EGCF是矩形 理由:∵
OA=OC,∴
AC=2OA.∵
AC=2AB,∴
AB=OA.∵
E是OB的中点,∴
AG⊥OB.∴
∠OEG=90°.同理,可得CF⊥OD,∴
AG∥CF.∴
EG∥CF.∵
EG=AE,OA=OC,∴
OE∥CG.∴
EF∥CG.∴
四边形EGCF是平行四边形.∵
∠OEG=90°,∴
四边形EGCF是矩形.
延长GM交DE于点H,连接BE,BF.∵
四边形ABDE和四边形BCFG都是正方形,∴
AB∥DE∥GF,∠EBD=∠FBG=45°.∴
∠HEM=∠GFM,∠EBF=90°.∵
M为EF的中点,∴
EM=FM=BM=EF.在△EHM和△FGM中,∴
△EHM≌△FGM.∴
HM=GM,EH=FG.∵
AB=2BC,∴
易得GF=EH=DH=DG.∴
△HDG为等腰直角三角形.设BC=1,则AB=2,BE=2,BF=,HG=.∴
MG=HG=,EF==.∴
MB=EF=.∴
==
1
一、
选择题
1.
(2019·盐城)如图,D,E分别是△ABC的边BA,BC的中点,AC=3,则DE的长为( )
A.
2
B.
C.
3
D.
2.
(2019·娄底)顺次连接菱形四边中点得到的四边形是( )
A.
平行四边形
B.
菱形
C.
矩形
D.
正方形
3.
(2019·铜仁)如图,D是△ABC内的一点,BD⊥CD,AD=7,BD=4,CD=3,E,F,G,H分别是AB,BD,CD,AC的中点,则四边形EFGH的周长为( )
A.
12
B.
14
C.
24
D.
21
4.
(2018·达州)如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M.若BC=7,则MN的长为( )
A.
B.
2
C.
D.
3
二、
填空题
5.
(2019·长沙)如图,要测量池塘两岸相对的A,B两点间的距离,可以在池塘外选一点C,连接AC,BC,分别取AC,BC的中点D,E,测得DE=50
m,则AB的长是________m.
6.
(2019·梧州)如图,在△ABC中,D,E分别是AB,AC的中点,F,G分别是AD,AE的中点,且FG=2
cm,则BC的长度是________cm.
7.
(2019·泰安)如图,在矩形ABCD中,AB=4,AD=2,E为AB的中点,F为EC上一动点,P为DF中点,连接PB,则PB的最小值是________.
三、
解答题
8.
(2019·徐州)如图,在矩形ABCD中,AC,BD交于点O,M,N分别为BC,OC的中点.若MN=4,求AC的长.
第8题
9.(2019·广元)如图,在△ABC中,∠BAC=90°,延长BA到点D,使AD=AB,E,F分别是边BC,AC的中点.求证:DF=BE.
第9题
10.(2019·湖州)如图,在△ABC中,D,E,F分别是AB,BC,AC的中点,连接DF,EF,BF.
(1)
求证:四边形BEFD是平行四边形;
(2)
若∠AFB=90°,AB=6,求四边形BEFD的周长.
第10题
11.(2019·扬州)如图,点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M,N分别是DC,DF的中点,连接MN.若AB=7,BE=5,求MN的长.
第11题
12.(2019·青岛)如图,在?ABCD中,对角线AC与BD相交于点O,E,F分别为OB,OD的中点,延长AE至点G,使EG=AE,连接CG,CF.
(1)
求证:△ABE≌△CDF.
(2)
当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.
第12题
13.(2019·淄博)如图,正方形ABDE和正方形BCFG的边AB,BC在同一条直线上,且AB=2BC,取EF的中点M.连接MD,MG,MB.求证:DM⊥MG,并求的值.
参考答案
一、
D
C
A
C
二、
100
8
2
三、
∵
M,N分别为BC,OC的中点,∴
BO=2MN=8.∵
四边形ABCD是矩形,∴
AC=BD=2BO=16
连接AE.∵
E,F分别是边BC,AC的中点,∴
EF∥AB,EF=AB.∵
AD=AB,∴
EF=AD.又∵
EF∥AD,∴
四边形ADFE是平行四边形.∴
DF=AE.∵
在Rt△ABC中,E是BC的中点,∴
AE=BC=BE=CE.∴
DF=BE
(1)
∵
D,E,F分别是AB,BC,AC的中点,∴
EF∥AB,DF∥BC.∴
四边形BEFD是平行四边形 (2)
∵
∠AFB=90°,D是AB的中点,∴
DF=DB=AB=3.∴
四边形BEFD是菱形.∴
BE=EF=DF=DB=3.∴
四边形BEFD的周长为4×3=12
如图,连接CF.∵
四边形ABCD和四边形BEFG都是正方形,∴
GF=GB=BE=5,BC=AB=7,∠G=90°.∴
GC=GB+BC=5+7=12.∴
CF===13.∵
M,N分别是DC,DF的中点,∴
MN=CF=
(1)
∵
四边形ABCD是平行四边形,∴
AB=CD,AB∥CD,OB=OD,OA=OC.∴
∠ABE=∠CDF.∵
E,F分别为OB,OD的中点,∴
BE=OB,DF=OD.∴
BE=DF.在△ABE和△CDF中,∴
△ABE≌△CDF (2)
当AC=2AB时,四边形EGCF是矩形 理由:∵
OA=OC,∴
AC=2OA.∵
AC=2AB,∴
AB=OA.∵
E是OB的中点,∴
AG⊥OB.∴
∠OEG=90°.同理,可得CF⊥OD,∴
AG∥CF.∴
EG∥CF.∵
EG=AE,OA=OC,∴
OE∥CG.∴
EF∥CG.∴
四边形EGCF是平行四边形.∵
∠OEG=90°,∴
四边形EGCF是矩形.
延长GM交DE于点H,连接BE,BF.∵
四边形ABDE和四边形BCFG都是正方形,∴
AB∥DE∥GF,∠EBD=∠FBG=45°.∴
∠HEM=∠GFM,∠EBF=90°.∵
M为EF的中点,∴
EM=FM=BM=EF.在△EHM和△FGM中,∴
△EHM≌△FGM.∴
HM=GM,EH=FG.∵
AB=2BC,∴
易得GF=EH=DH=DG.∴
△HDG为等腰直角三角形.设BC=1,则AB=2,BE=2,BF=,HG=.∴
MG=HG=,EF==.∴
MB=EF=.∴
==
