沪科版数学八年级下册19.3特殊的平行四边形中考题汇编(Word版 含答案)
文档属性
| 名称 | 沪科版数学八年级下册19.3特殊的平行四边形中考题汇编(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 114.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 00:00:00 | ||
图片预览


文档简介
沪科版数学八年级特殊的平行四边形中考题汇编
1
一、
选择题
1.
(2019·广州)如图,在矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F.若BE=3,AF=5,则AC的长为( )
A.
4
B.
4
C.
10
D.
8
2.
(2019·眉山)如图,在矩形ABCD中,AB=6,BC=8,过对角线交点O作EF⊥AC交AD于点E,交BC于点F,则DE的长是( )
A.
1
B.
C.
2
D.
3.
(2019·陕西)如图,在矩形ABCD中,AB=3,BC=6.若点E,F分别在AB,CD上,且BE=2AE,DF=2FC,G,H分别是AC的三等分点,则四边形EHFG的面积为( )
A.
1
B.
C.
2
D.
4
4.
(2019·永州)如图,四边形ABCD的对角线相交于点O,且O是BD的中点.若AB=AD=5,BD=8,∠ABD=∠CDB,则四边形ABCD的面积为( )
A.
40
B.
24
C.
20
D.
15
5.
(2019·大庆)下列说法中不正确的是( )
A.
四边相等的四边形是菱形
B.
对角线垂直的平行四边形是菱形
C.
菱形的对角线互相垂直且相等
D.
菱形的邻边相等
6.
(2019·呼和浩特)已知菱形的边长为3,较短的一条对角线的长为2,则该菱形较长的一条对角线的长为( )
A.
2
B.
2
C.
4
D.
2
7.
(2019·河北)如图,在菱形ABCD中,∠D=150°,则∠1的度数为( )
A.
30°
B.
25°
C.
20°
D.
15°
8.
(2019·宁夏)如图,四边形ABCD的两条对角线相交于点O,且互相平分.添加下列条件,仍不能判定四边形ABCD为菱形的是( )
A.
AC⊥BD
B.
AB=AD
C.
AC=BD
D.
∠ABD=∠CBD
9.
(2019·泸州)一个菱形的边长为6,面积为28,则该菱形的两条对角线的长度之和为( )
A.
8
B.
12
C.
16
D.
32
10.
(2019·赤峰)如图,菱形ABCD的周长为20,对角线AC,BD相交于点O,E是CD的中点,则OE的长是( )
A.
2.5
B.
3
C.
4
D.
5
11.
(2019·贵阳)如图,菱形ABCD的周长是4
cm,∠ABC=60°,那么这个菱形的对角线AC的长是( )
A.
1
cm
B.
2
cm
C.
3
cm
D.
4
cm
12.
(2019·深圳)如图,四边形ABCD为菱形,边长为4,点E,F分别在AB,AD上,且BE=AF,∠BAD=120°,有下列结论:①
△BEC≌△AFC;②
△ECF为等边三角形;③
∠AGE=∠AFC;④
若AF=1,则=.其中,正确的个数为( )
A.
1
B.
2
C.
3
D.
4
13.
(2019·绵阳)如图,在平面直角坐标系中,四边形OABC为菱形,O为原点,点A的坐标为(4,0),∠AOC=60°,则对角线的交点E的坐标为( )
A.
(2,)
B.
(,2)
C.
(,3)
D.
(3,)
14.
(2019·鄂尔多斯)如图,在正方形ABCD的外侧,作等边三角形ABE,则∠BED的度数为( )
A.
15°
B.
35°
C.
45°
D.
55°
15.
(2019·河池)如图,在正方形ABCD中,点E,F分别在BC,CD上,BE=CF,则图中与∠AEB相等的角的个数是( )
A.
1
B.
2
C.
3
D.
4
16.
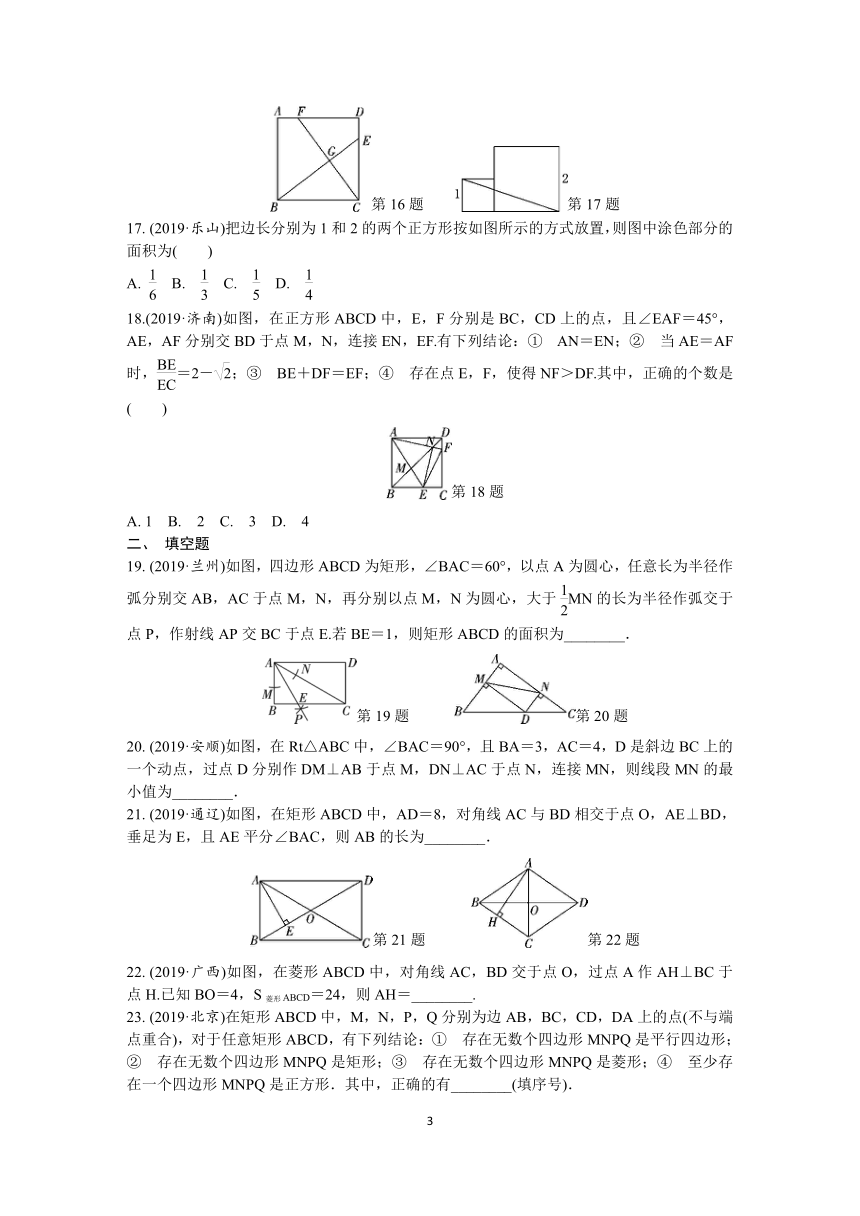
(2019·孝感)如图,在正方形ABCD中,点E,F分别在边CD,AD上,BE与CF交于点G.若BC=4,DE=AF=1,则GF的长为( )
A.
B.
C.
D.
17.
(2019·乐山)把边长分别为1和2的两个正方形按如图所示的方式放置,则图中涂色部分的面积为( )
A.
B.
C.
D.
18.(2019·济南)如图,在正方形ABCD中,E,F分别是BC,CD上的点,且∠EAF=45°,AE,AF分别交BD于点M,N,连接EN,EF.有下列结论:①
AN=EN;②
当AE=AF时,=2-;③
BE+DF=EF;④
存在点E,F,使得NF>DF.其中,正确的个数是( )
A.
1
B.
2
C.
3
D.
4
二、
填空题
19.
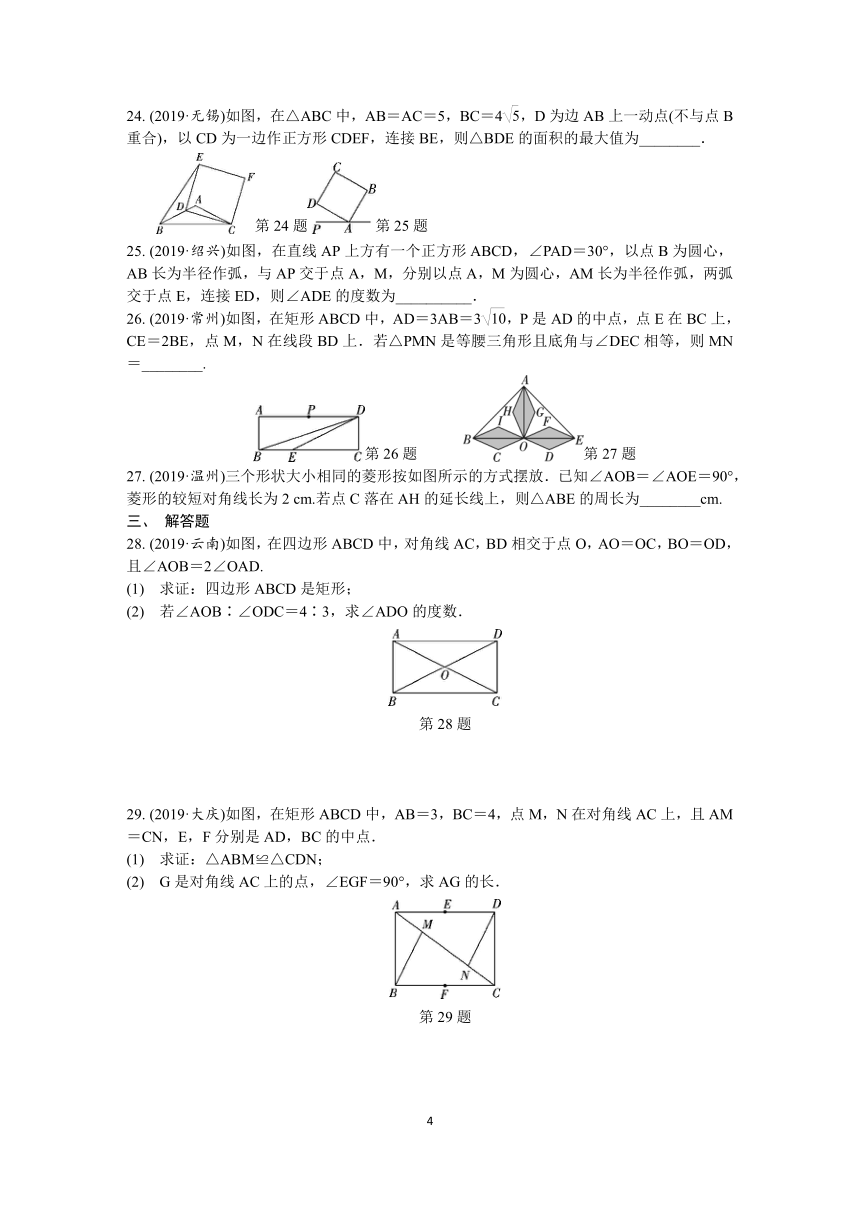
(2019·兰州)如图,四边形ABCD为矩形,∠BAC=60°,以点A为圆心,任意长为半径作弧分别交AB,AC于点M,N,再分别以点M,N为圆心,大于MN的长为半径作弧交于点P,作射线AP交BC于点E.若BE=1,则矩形ABCD的面积为________.
20.
(2019·安顺)如图,在Rt△ABC中,∠BAC=90°,且BA=3,AC=4,D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为________.
21.
(2019·通辽)如图,在矩形ABCD中,AD=8,对角线AC与BD相交于点O,AE⊥BD,垂足为E,且AE平分∠BAC,则AB的长为________.
22.
(2019·广西)如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AH⊥BC于点H.已知BO=4,S菱形ABCD=24,则AH=________.
23.
(2019·北京)在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合),对于任意矩形ABCD,有下列结论:①
存在无数个四边形MNPQ是平行四边形;②
存在无数个四边形MNPQ是矩形;③
存在无数个四边形MNPQ是菱形;④
至少存在一个四边形MNPQ是正方形.其中,正确的有________(填序号).
24.
(2019·无锡)如图,在△ABC中,AB=AC=5,BC=4,D为边AB上一动点(不与点B重合),以CD为一边作正方形CDEF,连接BE,则△BDE的面积的最大值为________.
25.
(2019·绍兴)如图,在直线AP上方有一个正方形ABCD,∠PAD=30°,以点B为圆心,AB长为半径作弧,与AP交于点A,M,分别以点A,M为圆心,AM长为半径作弧,两弧交于点E,连接ED,则∠ADE的度数为__________.
26.
(2019·常州)如图,在矩形ABCD中,AD=3AB=3,P是AD的中点,点E在BC上,CE=2BE,点M,N在线段BD上.若△PMN是等腰三角形且底角与∠DEC相等,则MN=________.
27.
(2019·温州)三个形状大小相同的菱形按如图所示的方式摆放.已知∠AOB=∠AOE=90°,菱形的较短对角线长为2
cm.若点C落在AH的延长线上,则△ABE的周长为________cm.
三、
解答题
28.
(2019·云南)如图,在四边形ABCD中,对角线AC,BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.
(1)
求证:四边形ABCD是矩形;
(2)
若∠AOB∶∠ODC=4∶3,求∠ADO的度数.
第28题
29.
(2019·大庆)如图,在矩形ABCD中,AB=3,BC=4,点M,N在对角线AC上,且AM=CN,E,F分别是AD,BC的中点.
(1)
求证:△ABM≌△CDN;
(2)
G是对角线AC上的点,∠EGF=90°,求AG的长.
第29题
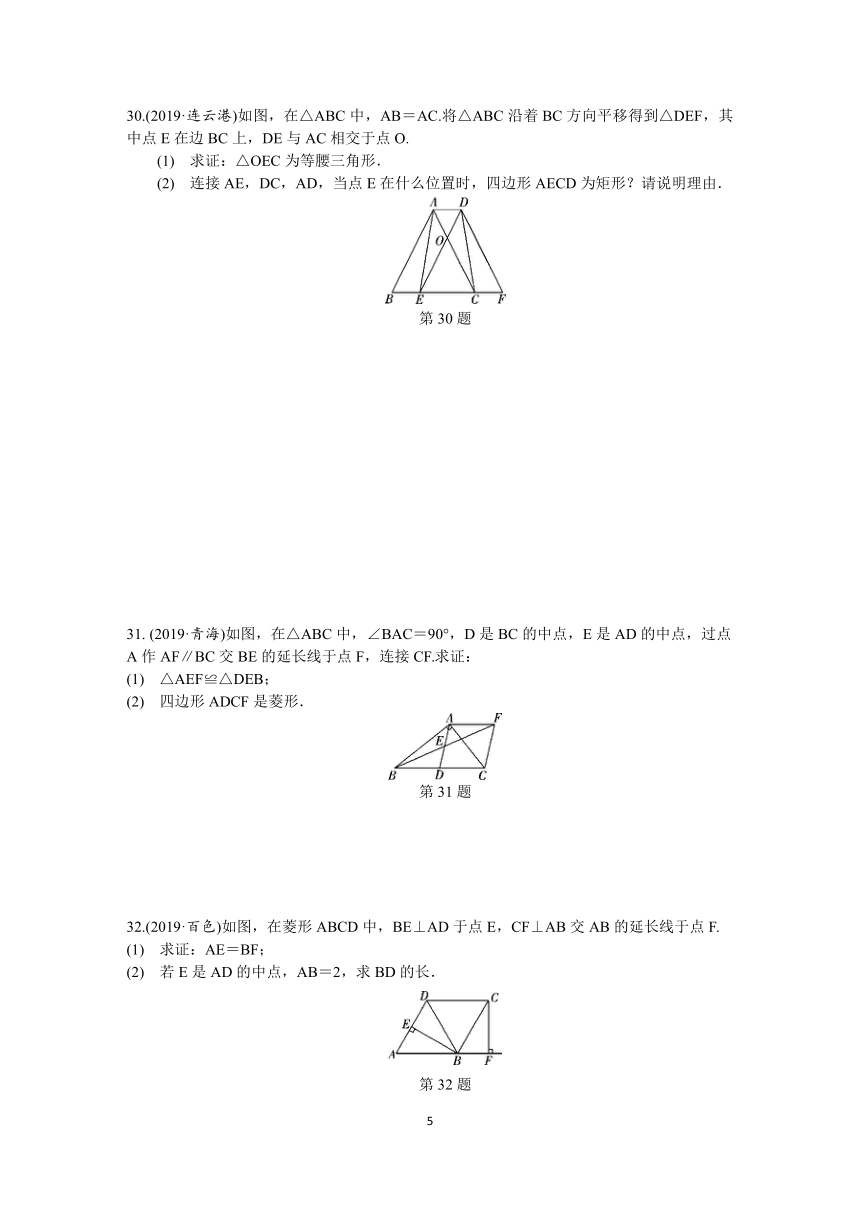
30.(2019·连云港)如图,在△ABC中,AB=AC.将△ABC沿着BC方向平移得到△DEF,其中点E在边BC上,DE与AC相交于点O.
(1)
求证:△OEC为等腰三角形.
(2)
连接AE,DC,AD,当点E在什么位置时,四边形AECD为矩形?请说明理由.
第30题
31.
(2019·青海)如图,在△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.求证:
(1)
△AEF≌△DEB;
(2)
四边形ADCF是菱形.
第31题
32.(2019·百色)如图,在菱形ABCD中,BE⊥AD于点E,CF⊥AB交AB的延长线于点F.
(1)
求证:AE=BF;
(2)
若E是AD的中点,AB=2,求BD的长.
第32题
33.(2019·贺州)如图,在矩形ABCD中,E,F分别是BC,AD边上的点,且AE=CF.
(1)
求证:△ABE≌△CDF.
(2)
当AC⊥EF时,四边形AECF是菱形吗?请说明理由.
第33题
34.(2019·天门)如图,E,F分别是正方形ABCD的边CB,DC的延长线上的点,且BE=CF,过点E作EG∥BF,交正方形外角的平分线CG于点G,连接AE,GF.求证:
(1)
AE⊥BF;
(2)
四边形BEGF是平行四边形.
第34题
35.(2019·杭州)如图,正方形ABCD的边长为1,正方形CEFG的面积为S1,点E在DC边上,点G在BC的延长线上.设以线段AD和DE为邻边的矩形的面积为S2,且S1=S2.
(1)
求线段CE的长;
(2)
若H为BC边的中点,连接HD,求证:HD=HG.
第35题
36.(2019·内江)如图,在正方形ABCD中,E是BC上的一点,F是CD的延长线上的一点,且BE=DF,连接AE,AF,EF.
(1)
求证:△ABE≌△ADF;
(2)
若AE=5,求EF的长.
第36题
37.
(2019·长沙)如图,在正方形ABCD中,点E,F分别在AD,CD上,且DE=CF,AF与BE相交于点G.
(1)
求证:BE=AF;
(2)
若AB=4,DE=1,求AG的长.
第37题
38.(2019·湘西州)如图,在正方形ABCD中,点E,F分别在边CD,AD上,且AF=CE.
(1)
求证:△ABF≌△CBE;
(2)
若AB=4,AF=1,求四边形BEDF的面积.
第38题
39.(2019·哈尔滨)在矩形ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F.
(1)
如图①,求证:AE=CF;
(2)
如图②,当∠ADB=30°时,连接AF,CE,在不添加任何辅助线的情况下,请直接写出图②中四个三角形,使写出的每个三角形的面积都等于矩形ABCD面积的,并说明理由.
40.(2019·绍兴)有一块形状如图所示的五边形余料ABCDE,AB=AE=6,BC=5,∠A=∠B=90°,∠C=135°,∠E>90°,要在这块余料中截取一块矩形材料,其中一条边在AE上,并使所截矩形材料的面积尽可能大.
(1)
若所截矩形材料的一条边是BC或AE,求矩形材料的面积.
(2)
能否截出比(1)中更大面积的矩形材料?如果能,求出这块矩形材料的面积的最大值;如果不能,请说明理由.
第40题
参考答案
一、
A
B
C
B
C
C
D
C
C
A
A
D
D
C
C
A
A
B
二、
3
①②③
8
15°或45°
6或
(12+8)
三、
(1)
∵
AO=OC,BO=OD,∴
四边形ABCD是平行四边形.∵
∠AOB=∠OAD+∠ADO=2∠OAD,∴
∠OAD=∠ADO.∴
AO=OD.∴
AC=BD.∴
四边形ABCD是矩形 (2)
∵
四边形ABCD是矩形,∴
∠ADC=90°.∴
∠ADO+∠ODC=90°.∵
∠AOB=2∠OAD,∠OAD=∠ADO,∴
∠AOB=2∠ADO.∵
∠AOB∶∠ODC=4∶3,∴
∠ADO∶∠ODC=2∶3.∴
∠ADO+∠ADO=90°.∴
∠ADO=36°
(1)
∵
四边形ABCD是矩形,∴
AB=CD,AB∥CD.∴
∠MAB=∠NCD.在△ABM和△CDN中,∴
△ABM≌△CDN (2)
如图,连接EF,交AC于点O.∵
四边形ABCD是矩形,∴
AD=BC,AD∥BC.∴
∠EAO=∠FCO.∵
E,F分别是AD,BC的中点,∴
AE=AD,CF=BC.∴
AE=CF.在△AEO和△CFO中,∴
△AEO≌△CFO.∴
EO=FO,AO=CO.∴
O为EF,AC的中点.在Rt△ABC中,∵
AB=3,BC=4,∴
AC==5.∴
AO=CO=.∵
∠EGF=90°,∴
OG=EF=.∴
AG=OA-OG=1或AG=OA+OG=4.∴
AG的长为1或4
(1)
∵
AB=AC,∴
∠B=∠ACB.∵
△ABC沿BC方向平移得到△DEF,∴
AB∥DE.∴
∠B=∠DEC.∴
∠ACB=∠DEC.∴
OE=OC,即△OEC为等腰三角形 (2)
当E为BC的中点时,四边形AECD是矩形.理由:∵
AB=AC,E为BC的中点,∴
AE⊥BC,BE=EC.∵
△ABC沿BC方向平移得到△DEF,∴
BE∥AD,BE=AD.∴
AD∥EC,AD=EC.∴
四边形AECD是平行四边形.∵
AE⊥BC,∴
∠AEC=90°.∴
四边形AECD是矩形.
(1)
∵
AF∥BC,∴
∠AFE=∠DBE.∵
E是AD的中点,∴
AE=DE.在△AEF和△DEB中,∴
△AEF≌△DEB (2)
由(1)知,△AEF≌△DEB,∴
AF=BD.∵
D是BC的中点,∴
BD=CD.∴
AF=CD.又∵
AF∥BC,∴
四边形ADCF是平行四边形.∵
∠BAC=90°,D是BC的中点,∴
AD=BC=CD.∴
四边形ADCF是菱形
(1)
∵
四边形ABCD是菱形,∴
AB=BC,AD∥BC.∴
∠A=∠CBF.∵
BE⊥AD,CF⊥AB,∴
∠AEB=∠BFC=90°.在△AEB和△BFC中,∴
△AEB≌△BFC.∴
AE=BF (2)
∵
E是AD的中点,BE⊥AD,∴
BD=AB=2
(1)
∵
四边形ABCD是矩形,∴
∠B=∠D=90°,AB=CD.在Rt△ABE和Rt△CDF中,∴
Rt△ABE≌Rt△CDF (2)
当AC⊥EF时,四边形AECF是菱形 理由:∵
△ABE≌△CDF,∴
BE=DF.∵
四边形ABCD是矩形,∴
BC∥AD,BC=AD.∴
BC-BE=AD-DF,即CE=AF.∵
CE∥AF,∴
四边形AECF是平行四边形.又∵
AC⊥EF,∴
四边形AECF是菱形.
(1)
∵
四边形ABCD是正方形,∴
AB=BC,∠ABC=∠BCD=90°.∴
∠ABE=∠BCF=90°.在△ABE和△BCF中,∴
△ABE≌△BCF.∴
∠BAE=∠CBF.∵
EG∥BF,∴
∠CBF=∠CEG.∴
∠BAE=∠CEG.∵
∠BAE+∠BEA=90°,∴
∠CEG+∠BEA=90°.∴
AE⊥EG.∴
AE⊥BF (2)
如图,延长AB至点P,使BP=BE,连接EP,则AP=CE,∠EBP=90°,∴
∠P=45°.∵
CG为正方形ABCD外角的平分线,∴
∠ECG=45°.∴
∠P=∠ECG.在△APE和△ECG中,∴
△APE≌△ECG.∴
AE=EG.∵
△ABE≌△BCF,∴
AE=BF.∴
EG=BF.∵
EG∥BF,∴
四边形BEGF是平行四边形
(1)
设正方形CEFG的边长为a.∵
正方形ABCD的边长为1,∴
DE=1-a.∵
S1=S2,∴
a2=1×(1-a),解得a=-(负值舍去).∴
线段CE的长是- (2)
∵
H为BC边的中点,BC=1,∴
CH=.∴
HD===.∵
CH=,CG=-,∴
HG=CH+CG=.∴
HD=HG
(1)
∵
四边形ABCD是正方形,∴
AB=AD,∠ABC=∠ADC=∠ADF=90°.在△ABE和△ADF中,∴
△ABE≌△ADF (2)
∵
△ABE≌△ADF,∴
AE=AF,∠BAE=∠DAF.∵
∠BAE+∠EAD=90°,∴
∠DAF+∠EAD=90°,即∠EAF=90°.∴
△AEF为等腰直角三角形.∴
EF=AE=5
(1)
∵
四边形ABCD是正方形,∴
∠BAE=∠ADF=90°,AB=AD=CD.∵
DE=CF,∴
AD-DE=CD-CF,即AE=DF.在△BAE和△ADF中,∴
△BAE≌△ADF.∴
BE=AF (2)
由(1)得△BAE≌△ADF,∴
∠EBA=∠FAD.∵
∠EBA+∠AEB=90°,∴
∠GAE+∠AEG=90°.∴
∠AGE=90°,即AG⊥BE.∵
AD=AB=4,DE=1,∴
AE=4-1=3.∴
BE==5.在Rt△ABE中,AB·AE=BE·AG,∴
AG==
(1)
∵
四边形ABCD是正方形,∴
AB=BC,∠A=∠C=90°.在△ABF和△CBE中,∴
△ABF≌△CBE (2)
∵
△ABF≌△CBE,∴
S△ABF=S△CBE=×4×1=2.∴
S四边形BEDF=42-2-2=12
(1)
∵
四边形ABCD是矩形,∴
AB=CD,AB∥CD.∴
∠ABE=∠CDF.∵
AE⊥BD,CF⊥BD,∴
∠AEB=∠CFD=90°.在△ABE和△CDF中,∴
△ABE≌△CDF.∴
AE=CF (2)
△ABE,△CDF,△BCE,△ADF 理由:∵
四边形ABCD是矩形,∴
∠BAD=90°.∵
∠ADB=30°,∴
AB=BD.∵
△ABE≌△CDF,∴
BE=DF,AE=CF.∴
S△ABE=S△CDF=S△BCE=S△ADF.易证△ABE∽△DBA,∴
==.又∵
S△DBA=S矩形ABCD,∴
=.∴
S△ABE=S△CDF=S△BCE=S△ADF=S矩形ABCD.
(1)
①
如图①,若所截矩形材料的一条边是BC,过点C作CF⊥AE于点F,则矩形材料的面积S1=AB·BC=6×5=30.②
如图②,若所截矩形材料的一条边是AE,过点E作EI⊥AE交CD于点I,过点I作IG⊥AB于点G,过点C作CH⊥IG于点H,则四边形AEIG为矩形,四边形BCHG为矩形.∴
IG=AE=6,HG=BC=5,CH=BG,∠HCB=90°.∴
IH=IG-HG=1.∵
∠BCD=135°,∴
∠ICH=45°.∴
△CHI为等腰直角三角形.∴
CH=IH=1.∴
BG=1.∴
AG=AB-BG=5.∴
矩形材料的面积S2=AE·AG=6×5=30.∴
若所截矩形材料的一条边是BC或AE,则矩形材料的面积是30 (2)
能.如图③,在CD上取点P,过点P作PM⊥AB于点M,PN⊥AE于点N,过点C作CQ⊥PM于点Q,则四边形ANPM为矩形,四边形BCQM为矩形.∴
MQ=BC,BM=CQ,∠QCB=90°.∵
∠BCD=135°,∴
∠PCQ=45°.∴
△PCQ为等腰直角三角形.∴
PQ=CQ.∴
PQ=BM.设AM=x,则BM=6-x,∴
PM=MQ+PQ=BC+BM=11-x.∴
矩形材料的面积S=AM·PM=x(11-x)=-(x-5.5)2+30.25.∵
-1<0,0当x=5.5时,S的最大值为30.25.∴
这块矩形材料的面积的最大值为30.25
1
一、
选择题
1.
(2019·广州)如图,在矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F.若BE=3,AF=5,则AC的长为( )
A.
4
B.
4
C.
10
D.
8
2.
(2019·眉山)如图,在矩形ABCD中,AB=6,BC=8,过对角线交点O作EF⊥AC交AD于点E,交BC于点F,则DE的长是( )
A.
1
B.
C.
2
D.
3.
(2019·陕西)如图,在矩形ABCD中,AB=3,BC=6.若点E,F分别在AB,CD上,且BE=2AE,DF=2FC,G,H分别是AC的三等分点,则四边形EHFG的面积为( )
A.
1
B.
C.
2
D.
4
4.
(2019·永州)如图,四边形ABCD的对角线相交于点O,且O是BD的中点.若AB=AD=5,BD=8,∠ABD=∠CDB,则四边形ABCD的面积为( )
A.
40
B.
24
C.
20
D.
15
5.
(2019·大庆)下列说法中不正确的是( )
A.
四边相等的四边形是菱形
B.
对角线垂直的平行四边形是菱形
C.
菱形的对角线互相垂直且相等
D.
菱形的邻边相等
6.
(2019·呼和浩特)已知菱形的边长为3,较短的一条对角线的长为2,则该菱形较长的一条对角线的长为( )
A.
2
B.
2
C.
4
D.
2
7.
(2019·河北)如图,在菱形ABCD中,∠D=150°,则∠1的度数为( )
A.
30°
B.
25°
C.
20°
D.
15°
8.
(2019·宁夏)如图,四边形ABCD的两条对角线相交于点O,且互相平分.添加下列条件,仍不能判定四边形ABCD为菱形的是( )
A.
AC⊥BD
B.
AB=AD
C.
AC=BD
D.
∠ABD=∠CBD
9.
(2019·泸州)一个菱形的边长为6,面积为28,则该菱形的两条对角线的长度之和为( )
A.
8
B.
12
C.
16
D.
32
10.
(2019·赤峰)如图,菱形ABCD的周长为20,对角线AC,BD相交于点O,E是CD的中点,则OE的长是( )
A.
2.5
B.
3
C.
4
D.
5
11.
(2019·贵阳)如图,菱形ABCD的周长是4
cm,∠ABC=60°,那么这个菱形的对角线AC的长是( )
A.
1
cm
B.
2
cm
C.
3
cm
D.
4
cm
12.
(2019·深圳)如图,四边形ABCD为菱形,边长为4,点E,F分别在AB,AD上,且BE=AF,∠BAD=120°,有下列结论:①
△BEC≌△AFC;②
△ECF为等边三角形;③
∠AGE=∠AFC;④
若AF=1,则=.其中,正确的个数为( )
A.
1
B.
2
C.
3
D.
4
13.
(2019·绵阳)如图,在平面直角坐标系中,四边形OABC为菱形,O为原点,点A的坐标为(4,0),∠AOC=60°,则对角线的交点E的坐标为( )
A.
(2,)
B.
(,2)
C.
(,3)
D.
(3,)
14.
(2019·鄂尔多斯)如图,在正方形ABCD的外侧,作等边三角形ABE,则∠BED的度数为( )
A.
15°
B.
35°
C.
45°
D.
55°
15.
(2019·河池)如图,在正方形ABCD中,点E,F分别在BC,CD上,BE=CF,则图中与∠AEB相等的角的个数是( )
A.
1
B.
2
C.
3
D.
4
16.
(2019·孝感)如图,在正方形ABCD中,点E,F分别在边CD,AD上,BE与CF交于点G.若BC=4,DE=AF=1,则GF的长为( )
A.
B.
C.
D.
17.
(2019·乐山)把边长分别为1和2的两个正方形按如图所示的方式放置,则图中涂色部分的面积为( )
A.
B.
C.
D.
18.(2019·济南)如图,在正方形ABCD中,E,F分别是BC,CD上的点,且∠EAF=45°,AE,AF分别交BD于点M,N,连接EN,EF.有下列结论:①
AN=EN;②
当AE=AF时,=2-;③
BE+DF=EF;④
存在点E,F,使得NF>DF.其中,正确的个数是( )
A.
1
B.
2
C.
3
D.
4
二、
填空题
19.
(2019·兰州)如图,四边形ABCD为矩形,∠BAC=60°,以点A为圆心,任意长为半径作弧分别交AB,AC于点M,N,再分别以点M,N为圆心,大于MN的长为半径作弧交于点P,作射线AP交BC于点E.若BE=1,则矩形ABCD的面积为________.
20.
(2019·安顺)如图,在Rt△ABC中,∠BAC=90°,且BA=3,AC=4,D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为________.
21.
(2019·通辽)如图,在矩形ABCD中,AD=8,对角线AC与BD相交于点O,AE⊥BD,垂足为E,且AE平分∠BAC,则AB的长为________.
22.
(2019·广西)如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AH⊥BC于点H.已知BO=4,S菱形ABCD=24,则AH=________.
23.
(2019·北京)在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合),对于任意矩形ABCD,有下列结论:①
存在无数个四边形MNPQ是平行四边形;②
存在无数个四边形MNPQ是矩形;③
存在无数个四边形MNPQ是菱形;④
至少存在一个四边形MNPQ是正方形.其中,正确的有________(填序号).
24.
(2019·无锡)如图,在△ABC中,AB=AC=5,BC=4,D为边AB上一动点(不与点B重合),以CD为一边作正方形CDEF,连接BE,则△BDE的面积的最大值为________.
25.
(2019·绍兴)如图,在直线AP上方有一个正方形ABCD,∠PAD=30°,以点B为圆心,AB长为半径作弧,与AP交于点A,M,分别以点A,M为圆心,AM长为半径作弧,两弧交于点E,连接ED,则∠ADE的度数为__________.
26.
(2019·常州)如图,在矩形ABCD中,AD=3AB=3,P是AD的中点,点E在BC上,CE=2BE,点M,N在线段BD上.若△PMN是等腰三角形且底角与∠DEC相等,则MN=________.
27.
(2019·温州)三个形状大小相同的菱形按如图所示的方式摆放.已知∠AOB=∠AOE=90°,菱形的较短对角线长为2
cm.若点C落在AH的延长线上,则△ABE的周长为________cm.
三、
解答题
28.
(2019·云南)如图,在四边形ABCD中,对角线AC,BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.
(1)
求证:四边形ABCD是矩形;
(2)
若∠AOB∶∠ODC=4∶3,求∠ADO的度数.
第28题
29.
(2019·大庆)如图,在矩形ABCD中,AB=3,BC=4,点M,N在对角线AC上,且AM=CN,E,F分别是AD,BC的中点.
(1)
求证:△ABM≌△CDN;
(2)
G是对角线AC上的点,∠EGF=90°,求AG的长.
第29题
30.(2019·连云港)如图,在△ABC中,AB=AC.将△ABC沿着BC方向平移得到△DEF,其中点E在边BC上,DE与AC相交于点O.
(1)
求证:△OEC为等腰三角形.
(2)
连接AE,DC,AD,当点E在什么位置时,四边形AECD为矩形?请说明理由.
第30题
31.
(2019·青海)如图,在△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.求证:
(1)
△AEF≌△DEB;
(2)
四边形ADCF是菱形.
第31题
32.(2019·百色)如图,在菱形ABCD中,BE⊥AD于点E,CF⊥AB交AB的延长线于点F.
(1)
求证:AE=BF;
(2)
若E是AD的中点,AB=2,求BD的长.
第32题
33.(2019·贺州)如图,在矩形ABCD中,E,F分别是BC,AD边上的点,且AE=CF.
(1)
求证:△ABE≌△CDF.
(2)
当AC⊥EF时,四边形AECF是菱形吗?请说明理由.
第33题
34.(2019·天门)如图,E,F分别是正方形ABCD的边CB,DC的延长线上的点,且BE=CF,过点E作EG∥BF,交正方形外角的平分线CG于点G,连接AE,GF.求证:
(1)
AE⊥BF;
(2)
四边形BEGF是平行四边形.
第34题
35.(2019·杭州)如图,正方形ABCD的边长为1,正方形CEFG的面积为S1,点E在DC边上,点G在BC的延长线上.设以线段AD和DE为邻边的矩形的面积为S2,且S1=S2.
(1)
求线段CE的长;
(2)
若H为BC边的中点,连接HD,求证:HD=HG.
第35题
36.(2019·内江)如图,在正方形ABCD中,E是BC上的一点,F是CD的延长线上的一点,且BE=DF,连接AE,AF,EF.
(1)
求证:△ABE≌△ADF;
(2)
若AE=5,求EF的长.
第36题
37.
(2019·长沙)如图,在正方形ABCD中,点E,F分别在AD,CD上,且DE=CF,AF与BE相交于点G.
(1)
求证:BE=AF;
(2)
若AB=4,DE=1,求AG的长.
第37题
38.(2019·湘西州)如图,在正方形ABCD中,点E,F分别在边CD,AD上,且AF=CE.
(1)
求证:△ABF≌△CBE;
(2)
若AB=4,AF=1,求四边形BEDF的面积.
第38题
39.(2019·哈尔滨)在矩形ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F.
(1)
如图①,求证:AE=CF;
(2)
如图②,当∠ADB=30°时,连接AF,CE,在不添加任何辅助线的情况下,请直接写出图②中四个三角形,使写出的每个三角形的面积都等于矩形ABCD面积的,并说明理由.
40.(2019·绍兴)有一块形状如图所示的五边形余料ABCDE,AB=AE=6,BC=5,∠A=∠B=90°,∠C=135°,∠E>90°,要在这块余料中截取一块矩形材料,其中一条边在AE上,并使所截矩形材料的面积尽可能大.
(1)
若所截矩形材料的一条边是BC或AE,求矩形材料的面积.
(2)
能否截出比(1)中更大面积的矩形材料?如果能,求出这块矩形材料的面积的最大值;如果不能,请说明理由.
第40题
参考答案
一、
A
B
C
B
C
C
D
C
C
A
A
D
D
C
C
A
A
B
二、
3
①②③
8
15°或45°
6或
(12+8)
三、
(1)
∵
AO=OC,BO=OD,∴
四边形ABCD是平行四边形.∵
∠AOB=∠OAD+∠ADO=2∠OAD,∴
∠OAD=∠ADO.∴
AO=OD.∴
AC=BD.∴
四边形ABCD是矩形 (2)
∵
四边形ABCD是矩形,∴
∠ADC=90°.∴
∠ADO+∠ODC=90°.∵
∠AOB=2∠OAD,∠OAD=∠ADO,∴
∠AOB=2∠ADO.∵
∠AOB∶∠ODC=4∶3,∴
∠ADO∶∠ODC=2∶3.∴
∠ADO+∠ADO=90°.∴
∠ADO=36°
(1)
∵
四边形ABCD是矩形,∴
AB=CD,AB∥CD.∴
∠MAB=∠NCD.在△ABM和△CDN中,∴
△ABM≌△CDN (2)
如图,连接EF,交AC于点O.∵
四边形ABCD是矩形,∴
AD=BC,AD∥BC.∴
∠EAO=∠FCO.∵
E,F分别是AD,BC的中点,∴
AE=AD,CF=BC.∴
AE=CF.在△AEO和△CFO中,∴
△AEO≌△CFO.∴
EO=FO,AO=CO.∴
O为EF,AC的中点.在Rt△ABC中,∵
AB=3,BC=4,∴
AC==5.∴
AO=CO=.∵
∠EGF=90°,∴
OG=EF=.∴
AG=OA-OG=1或AG=OA+OG=4.∴
AG的长为1或4
(1)
∵
AB=AC,∴
∠B=∠ACB.∵
△ABC沿BC方向平移得到△DEF,∴
AB∥DE.∴
∠B=∠DEC.∴
∠ACB=∠DEC.∴
OE=OC,即△OEC为等腰三角形 (2)
当E为BC的中点时,四边形AECD是矩形.理由:∵
AB=AC,E为BC的中点,∴
AE⊥BC,BE=EC.∵
△ABC沿BC方向平移得到△DEF,∴
BE∥AD,BE=AD.∴
AD∥EC,AD=EC.∴
四边形AECD是平行四边形.∵
AE⊥BC,∴
∠AEC=90°.∴
四边形AECD是矩形.
(1)
∵
AF∥BC,∴
∠AFE=∠DBE.∵
E是AD的中点,∴
AE=DE.在△AEF和△DEB中,∴
△AEF≌△DEB (2)
由(1)知,△AEF≌△DEB,∴
AF=BD.∵
D是BC的中点,∴
BD=CD.∴
AF=CD.又∵
AF∥BC,∴
四边形ADCF是平行四边形.∵
∠BAC=90°,D是BC的中点,∴
AD=BC=CD.∴
四边形ADCF是菱形
(1)
∵
四边形ABCD是菱形,∴
AB=BC,AD∥BC.∴
∠A=∠CBF.∵
BE⊥AD,CF⊥AB,∴
∠AEB=∠BFC=90°.在△AEB和△BFC中,∴
△AEB≌△BFC.∴
AE=BF (2)
∵
E是AD的中点,BE⊥AD,∴
BD=AB=2
(1)
∵
四边形ABCD是矩形,∴
∠B=∠D=90°,AB=CD.在Rt△ABE和Rt△CDF中,∴
Rt△ABE≌Rt△CDF (2)
当AC⊥EF时,四边形AECF是菱形 理由:∵
△ABE≌△CDF,∴
BE=DF.∵
四边形ABCD是矩形,∴
BC∥AD,BC=AD.∴
BC-BE=AD-DF,即CE=AF.∵
CE∥AF,∴
四边形AECF是平行四边形.又∵
AC⊥EF,∴
四边形AECF是菱形.
(1)
∵
四边形ABCD是正方形,∴
AB=BC,∠ABC=∠BCD=90°.∴
∠ABE=∠BCF=90°.在△ABE和△BCF中,∴
△ABE≌△BCF.∴
∠BAE=∠CBF.∵
EG∥BF,∴
∠CBF=∠CEG.∴
∠BAE=∠CEG.∵
∠BAE+∠BEA=90°,∴
∠CEG+∠BEA=90°.∴
AE⊥EG.∴
AE⊥BF (2)
如图,延长AB至点P,使BP=BE,连接EP,则AP=CE,∠EBP=90°,∴
∠P=45°.∵
CG为正方形ABCD外角的平分线,∴
∠ECG=45°.∴
∠P=∠ECG.在△APE和△ECG中,∴
△APE≌△ECG.∴
AE=EG.∵
△ABE≌△BCF,∴
AE=BF.∴
EG=BF.∵
EG∥BF,∴
四边形BEGF是平行四边形
(1)
设正方形CEFG的边长为a.∵
正方形ABCD的边长为1,∴
DE=1-a.∵
S1=S2,∴
a2=1×(1-a),解得a=-(负值舍去).∴
线段CE的长是- (2)
∵
H为BC边的中点,BC=1,∴
CH=.∴
HD===.∵
CH=,CG=-,∴
HG=CH+CG=.∴
HD=HG
(1)
∵
四边形ABCD是正方形,∴
AB=AD,∠ABC=∠ADC=∠ADF=90°.在△ABE和△ADF中,∴
△ABE≌△ADF (2)
∵
△ABE≌△ADF,∴
AE=AF,∠BAE=∠DAF.∵
∠BAE+∠EAD=90°,∴
∠DAF+∠EAD=90°,即∠EAF=90°.∴
△AEF为等腰直角三角形.∴
EF=AE=5
(1)
∵
四边形ABCD是正方形,∴
∠BAE=∠ADF=90°,AB=AD=CD.∵
DE=CF,∴
AD-DE=CD-CF,即AE=DF.在△BAE和△ADF中,∴
△BAE≌△ADF.∴
BE=AF (2)
由(1)得△BAE≌△ADF,∴
∠EBA=∠FAD.∵
∠EBA+∠AEB=90°,∴
∠GAE+∠AEG=90°.∴
∠AGE=90°,即AG⊥BE.∵
AD=AB=4,DE=1,∴
AE=4-1=3.∴
BE==5.在Rt△ABE中,AB·AE=BE·AG,∴
AG==
(1)
∵
四边形ABCD是正方形,∴
AB=BC,∠A=∠C=90°.在△ABF和△CBE中,∴
△ABF≌△CBE (2)
∵
△ABF≌△CBE,∴
S△ABF=S△CBE=×4×1=2.∴
S四边形BEDF=42-2-2=12
(1)
∵
四边形ABCD是矩形,∴
AB=CD,AB∥CD.∴
∠ABE=∠CDF.∵
AE⊥BD,CF⊥BD,∴
∠AEB=∠CFD=90°.在△ABE和△CDF中,∴
△ABE≌△CDF.∴
AE=CF (2)
△ABE,△CDF,△BCE,△ADF 理由:∵
四边形ABCD是矩形,∴
∠BAD=90°.∵
∠ADB=30°,∴
AB=BD.∵
△ABE≌△CDF,∴
BE=DF,AE=CF.∴
S△ABE=S△CDF=S△BCE=S△ADF.易证△ABE∽△DBA,∴
==.又∵
S△DBA=S矩形ABCD,∴
=.∴
S△ABE=S△CDF=S△BCE=S△ADF=S矩形ABCD.
(1)
①
如图①,若所截矩形材料的一条边是BC,过点C作CF⊥AE于点F,则矩形材料的面积S1=AB·BC=6×5=30.②
如图②,若所截矩形材料的一条边是AE,过点E作EI⊥AE交CD于点I,过点I作IG⊥AB于点G,过点C作CH⊥IG于点H,则四边形AEIG为矩形,四边形BCHG为矩形.∴
IG=AE=6,HG=BC=5,CH=BG,∠HCB=90°.∴
IH=IG-HG=1.∵
∠BCD=135°,∴
∠ICH=45°.∴
△CHI为等腰直角三角形.∴
CH=IH=1.∴
BG=1.∴
AG=AB-BG=5.∴
矩形材料的面积S2=AE·AG=6×5=30.∴
若所截矩形材料的一条边是BC或AE,则矩形材料的面积是30 (2)
能.如图③,在CD上取点P,过点P作PM⊥AB于点M,PN⊥AE于点N,过点C作CQ⊥PM于点Q,则四边形ANPM为矩形,四边形BCQM为矩形.∴
MQ=BC,BM=CQ,∠QCB=90°.∵
∠BCD=135°,∴
∠PCQ=45°.∴
△PCQ为等腰直角三角形.∴
PQ=CQ.∴
PQ=BM.设AM=x,则BM=6-x,∴
PM=MQ+PQ=BC+BM=11-x.∴
矩形材料的面积S=AM·PM=x(11-x)=-(x-5.5)2+30.25.∵
-1<0,0
这块矩形材料的面积的最大值为30.25
