4.3.2 角的比较与运算 第一课时 课件(共24张PPT)
文档属性
| 名称 | 4.3.2 角的比较与运算 第一课时 课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 06:54:39 | ||
图片预览








文档简介
(共24张PPT)
人教版
七上
第四章
几何图形初步
4.3.2
角的比较与运算
(第1课时)
教学重点:
角的比较,用符号表示角的和差关系.
教学难点:
角的和差运算及角度制的度、分、秒的有关运算.
复习回顾
1.角的表示方法有哪些?
(1).三个大写字母,顶点写在中间.
(2).一个大写字母(只适用于单独一个角).
(3).用数字表示.
(4).用希腊字母表示.
2.
比较线段大小有哪些方法呢?
(1).度量法
(2).叠合法
能类似比较线段大小来比较角的大小吗?
探究新知
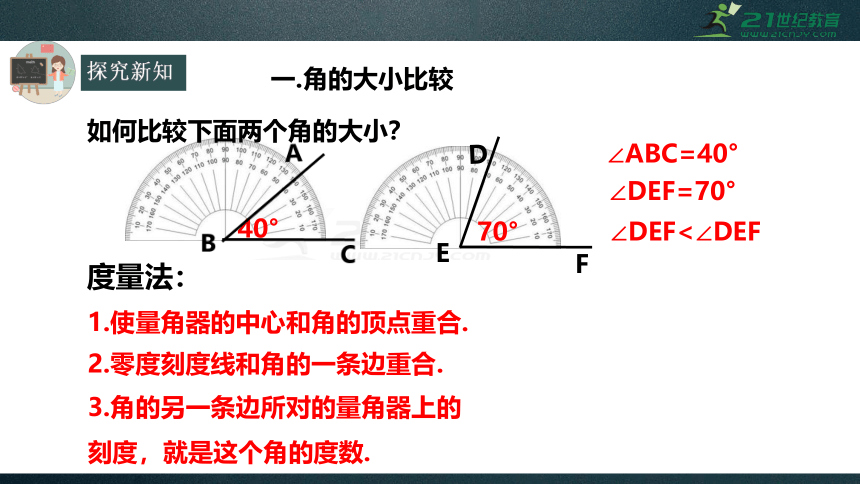
一.角的大小比较
如何比较下面两个角的大小?
1.使量角器的中心和角的顶点重合.
2.零度刻度线和角的一条边重合.
3.角的另一条边所对的量角器上的刻度,就是这个角的度数.
E
F
D
∠ABC=40°
40°
70°
∠DEF=70°
∠DEF<∠DEF
度量法:
探究新知
①将∠ABC的顶点B与∠DEF的顶点E重合.
E
F
D
如何比较∠ABC与∠DEF的大小?
③如果AB边在∠DEF的内部,那么∠ABC小于∠DEF.
记作为:∠ABC<∠DEF
②边BC与EF其重叠.
B
C
A
叠合法:
探究新知
①将∠ABC的顶点B与∠DEF的顶点E重合.
E
F
D
如何比较∠ABC与∠DEF的大小?
③如果AB边与DE边重合,那么∠ABC等于∠DEF.
记作为:∠ABC=∠DEF
②边BC与EF其重叠.
B
C
A
探究新知
①将∠ABC的顶点B与∠DEF的顶点E重合.
E
F
D
如何比较∠ABC与∠DEF的大小?
③如果AB边在∠DEF的外部,那么∠ABC大于∠DEF.
记作为:∠ABC>∠DEF
②边BC与EF其重叠.
B
C
A
探究新知
E
F
D
2.角的大小与角的两条边张开的程度有关,张开的越大,角就越大,相反张开的越小,角则越小.
1.角的大小与边的长短无关.
45°
70°
探究新知
如图,共有几个角?它们之间有什么关系?
答:有三个角.
∠AOC是∠AOB与∠BOC的和,记作∠AOC=∠AOB+∠BOC.
∠AOB是∠AOC与∠BOC的差,记作∠AOB=
.
∠BOC是∠AOC与∠AOB的差,记作∠BOC=
.
O
A
B
C
∠AOC-∠AOB
∠AOC-∠BOC
关系是:
二.角的和差
例题讲解
例1如图O是直线AB上一点,∠
AOC=53°17’,求∠
BOC的度数.
=126°43'.
分析∶AB是直线,
∠
AOB
是平角.
∠
BOC与∠
AOC的和是∠
AOB.
解∶由题意可知,
∠
AOB是平角,
∠
AOB=∠
BOC+∠
AOC.
所以∠
BOC=
∠
AOB-
∠
AOC
=180°-53°17'
练一练
解:
∵
∠AOC=122°,
∠BOC=48°
∴∠AOB=∠AOC-
∠BOC
=122°-48°
=74°
如图,已知∠AOC=122°,∠BOC=48°,求∠AOB的度数.
练一练
如图,借助三角尺画出15°,75°的角.
用一副三角板还可以画出哪些度数的角?
105°
120°
150°
135°
75°
15°
探究新知
三.角度的有运算
计算:18°16'48″
+23°45'23″
1.角度的加法运算.
解:18°16'48″
+23°45'23″
=(18+23)°+(16+45)’+(48+23)″
=41°+61’+71″
逢60要进位
=41°+62'11″
=42°2'11″
逢60要进位
探究新知
三.角度的有运算
计算:28°35'48
″
-20°45'53″
2.角度的减法运算.
解:
28°35'48
″
-20°45'53″
=
28°34'108
″
-20°45'53″
=
27°94'108
″
-20°45'53″
=7°49'55″
1作60,1’=60
″
1作60,1°=60'
探究新知
三.角度的有运算
计算:14°12′23″×5
3.角度的乘法运算.
解:
14°12′23″×5
=70°60′115″
=70°61′55″
=71°1′55″
例题讲解
例2.把一个周角分为7等分,每一份是多少度?(精确到分)
答:每一份是51°26’的角.
三.角度的有运算
4.角度的除法运算.
解:
360°÷7
=
51°+3°÷7
=51°+180’
÷7
≈
51°26’
课堂练习
2.已知∠AOB=17°,∠BOC=53°,则∠AOC等于(
)
A
70°
B
60°
C
36°
D
70°或
36°.
1.如图,已知∠AOB=∠COD,则(
).
A
∠
1>
∠
2
B
∠
1=
∠
2
C
∠
1<
∠
2
D
∠
1与∠
2
的大小关系不确定
B
D
课堂练习
B
∠AOC=∠AOD-
∠COD
A
∠AOB=∠AOC-∠BOC
3.如图,下列式子错误的是(
).
D
∠BOD=∠COD+∠BOC
C
∠BOC=∠BOD-∠AOC
C
课堂练习
4.计算:(1)34°18′13″
-15°32′43″
解:
34°18′13″
-15°32′43″
=
34°17′73″
-15°32′43″
=
33°77′73″
-15°32′43″
=
18°45′40″
(2)78°16’+
35°53′18″
解:78°16’+
35°53′18″
=113°69′18″
=114°9′18″
课堂练习
(3)15°43′26″×3
解:15°43′26″×3
=45°129′78″
=45°130′18″
=47°10′18″
解:
52°15′÷3
=
17°+1°15′÷3
=17°+75′÷3
(4)52°15′÷3
=17°+25′
=17°25′
课堂练习
解:
∵
∠AOD=90°,∠BOC=25°,
∠COD=38°
∴∠AOB=
∠AOC
-∠BOC-
∠COD
=90°-25°
-38°
=27°
5.如图,已知∠AOD=90°,∠BOC=25°,
∠COD=38°,求∠AOB和∠BOD的度数.
∠BOD=∠BOC+∠COD
=25°+38°
=63°
课堂小结
三.角度的有运算:
一.角的大小比较的两种方法:
2.叠合法
1.度量法
二.角的和差.
1.度与度、分与分、秒与秒分别相加减,分秒相加逢60要进位,
相减时要借1当作60(借1°作60′;借1′作60").
2.除法先从度开始除,除不尽转化为分,再除不尽转化为秒,直到精确度要求的位数为止.
课外作业
习题4.3
第136页第3题
第136页第6题
https://www.21cnjy.com/help/help_extract.php
人教版
七上
第四章
几何图形初步
4.3.2
角的比较与运算
(第1课时)
教学重点:
角的比较,用符号表示角的和差关系.
教学难点:
角的和差运算及角度制的度、分、秒的有关运算.
复习回顾
1.角的表示方法有哪些?
(1).三个大写字母,顶点写在中间.
(2).一个大写字母(只适用于单独一个角).
(3).用数字表示.
(4).用希腊字母表示.
2.
比较线段大小有哪些方法呢?
(1).度量法
(2).叠合法
能类似比较线段大小来比较角的大小吗?
探究新知
一.角的大小比较
如何比较下面两个角的大小?
1.使量角器的中心和角的顶点重合.
2.零度刻度线和角的一条边重合.
3.角的另一条边所对的量角器上的刻度,就是这个角的度数.
E
F
D
∠ABC=40°
40°
70°
∠DEF=70°
∠DEF<∠DEF
度量法:
探究新知
①将∠ABC的顶点B与∠DEF的顶点E重合.
E
F
D
如何比较∠ABC与∠DEF的大小?
③如果AB边在∠DEF的内部,那么∠ABC小于∠DEF.
记作为:∠ABC<∠DEF
②边BC与EF其重叠.
B
C
A
叠合法:
探究新知
①将∠ABC的顶点B与∠DEF的顶点E重合.
E
F
D
如何比较∠ABC与∠DEF的大小?
③如果AB边与DE边重合,那么∠ABC等于∠DEF.
记作为:∠ABC=∠DEF
②边BC与EF其重叠.
B
C
A
探究新知
①将∠ABC的顶点B与∠DEF的顶点E重合.
E
F
D
如何比较∠ABC与∠DEF的大小?
③如果AB边在∠DEF的外部,那么∠ABC大于∠DEF.
记作为:∠ABC>∠DEF
②边BC与EF其重叠.
B
C
A
探究新知
E
F
D
2.角的大小与角的两条边张开的程度有关,张开的越大,角就越大,相反张开的越小,角则越小.
1.角的大小与边的长短无关.
45°
70°
探究新知
如图,共有几个角?它们之间有什么关系?
答:有三个角.
∠AOC是∠AOB与∠BOC的和,记作∠AOC=∠AOB+∠BOC.
∠AOB是∠AOC与∠BOC的差,记作∠AOB=
.
∠BOC是∠AOC与∠AOB的差,记作∠BOC=
.
O
A
B
C
∠AOC-∠AOB
∠AOC-∠BOC
关系是:
二.角的和差
例题讲解
例1如图O是直线AB上一点,∠
AOC=53°17’,求∠
BOC的度数.
=126°43'.
分析∶AB是直线,
∠
AOB
是平角.
∠
BOC与∠
AOC的和是∠
AOB.
解∶由题意可知,
∠
AOB是平角,
∠
AOB=∠
BOC+∠
AOC.
所以∠
BOC=
∠
AOB-
∠
AOC
=180°-53°17'
练一练
解:
∵
∠AOC=122°,
∠BOC=48°
∴∠AOB=∠AOC-
∠BOC
=122°-48°
=74°
如图,已知∠AOC=122°,∠BOC=48°,求∠AOB的度数.
练一练
如图,借助三角尺画出15°,75°的角.
用一副三角板还可以画出哪些度数的角?
105°
120°
150°
135°
75°
15°
探究新知
三.角度的有运算
计算:18°16'48″
+23°45'23″
1.角度的加法运算.
解:18°16'48″
+23°45'23″
=(18+23)°+(16+45)’+(48+23)″
=41°+61’+71″
逢60要进位
=41°+62'11″
=42°2'11″
逢60要进位
探究新知
三.角度的有运算
计算:28°35'48
″
-20°45'53″
2.角度的减法运算.
解:
28°35'48
″
-20°45'53″
=
28°34'108
″
-20°45'53″
=
27°94'108
″
-20°45'53″
=7°49'55″
1作60,1’=60
″
1作60,1°=60'
探究新知
三.角度的有运算
计算:14°12′23″×5
3.角度的乘法运算.
解:
14°12′23″×5
=70°60′115″
=70°61′55″
=71°1′55″
例题讲解
例2.把一个周角分为7等分,每一份是多少度?(精确到分)
答:每一份是51°26’的角.
三.角度的有运算
4.角度的除法运算.
解:
360°÷7
=
51°+3°÷7
=51°+180’
÷7
≈
51°26’
课堂练习
2.已知∠AOB=17°,∠BOC=53°,则∠AOC等于(
)
A
70°
B
60°
C
36°
D
70°或
36°.
1.如图,已知∠AOB=∠COD,则(
).
A
∠
1>
∠
2
B
∠
1=
∠
2
C
∠
1<
∠
2
D
∠
1与∠
2
的大小关系不确定
B
D
课堂练习
B
∠AOC=∠AOD-
∠COD
A
∠AOB=∠AOC-∠BOC
3.如图,下列式子错误的是(
).
D
∠BOD=∠COD+∠BOC
C
∠BOC=∠BOD-∠AOC
C
课堂练习
4.计算:(1)34°18′13″
-15°32′43″
解:
34°18′13″
-15°32′43″
=
34°17′73″
-15°32′43″
=
33°77′73″
-15°32′43″
=
18°45′40″
(2)78°16’+
35°53′18″
解:78°16’+
35°53′18″
=113°69′18″
=114°9′18″
课堂练习
(3)15°43′26″×3
解:15°43′26″×3
=45°129′78″
=45°130′18″
=47°10′18″
解:
52°15′÷3
=
17°+1°15′÷3
=17°+75′÷3
(4)52°15′÷3
=17°+25′
=17°25′
课堂练习
解:
∵
∠AOD=90°,∠BOC=25°,
∠COD=38°
∴∠AOB=
∠AOC
-∠BOC-
∠COD
=90°-25°
-38°
=27°
5.如图,已知∠AOD=90°,∠BOC=25°,
∠COD=38°,求∠AOB和∠BOD的度数.
∠BOD=∠BOC+∠COD
=25°+38°
=63°
课堂小结
三.角度的有运算:
一.角的大小比较的两种方法:
2.叠合法
1.度量法
二.角的和差.
1.度与度、分与分、秒与秒分别相加减,分秒相加逢60要进位,
相减时要借1当作60(借1°作60′;借1′作60").
2.除法先从度开始除,除不尽转化为分,再除不尽转化为秒,直到精确度要求的位数为止.
课外作业
习题4.3
第136页第3题
第136页第6题
https://www.21cnjy.com/help/help_extract.php
