六年级数学下册六整理和复习5综合与实践6.15有趣的平衡教学课件(15张PPT)新人教版
文档属性
| 名称 | 六年级数学下册六整理和复习5综合与实践6.15有趣的平衡教学课件(15张PPT)新人教版 |

|
|
| 格式 | zip | ||
| 文件大小 | 1022.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 20:17:42 | ||
图片预览






文档简介
(共15张PPT)
整理和复习
第15课时
有趣的平衡
一、新课导入
同学们,你听说过“杠杆原理”吗?
知道它在生活中的应用吗?可能大家
都没有想到,杠杆原理的背后隐藏着
数学原理,那就是反比例关系。
下面就让我们通过实验体验它的奥秘吧。
二、探究新知
准备选一根粗细均匀的竹竿(长约1m),在中点的位置打个孔并栓上绳子,然后从中点开始每隔8cm做一个记号。
①准备的竹竿长度是1m,尽量做到粗细均匀。
②在竹竿中点处打孔栓绳子时注意绳子的长度,同时注意检查拎起绳子后竹竿是否平衡。
③从中点处开始每隔8㎝做一个刻度记号,尽量等距。
④选用的棋子、装棋子的塑料袋要完全一样。
实验条件控制
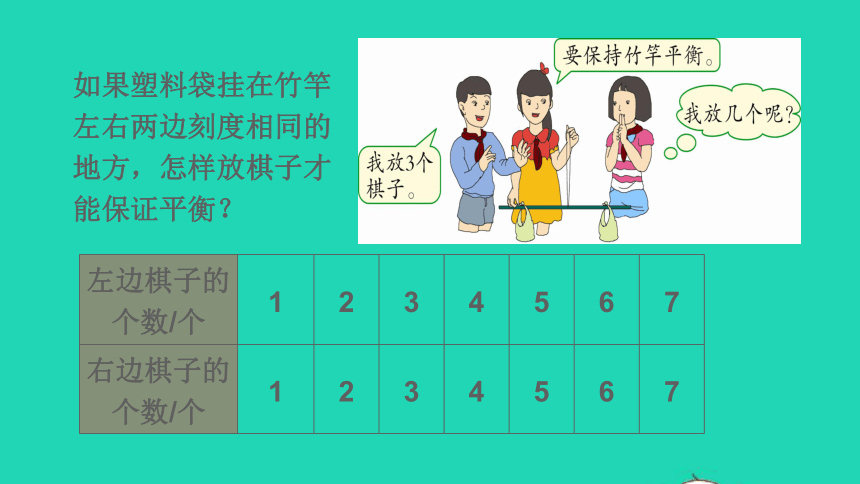
如果塑料袋挂在竹竿
左右两边刻度相同的
地方,怎样放棋子才
能保证平衡?
左边棋子的个数/个
1
2
3
4
5
6
7
右边棋子的个数/个
1
2
3
4
5
6
7
如果左右两个塑料袋放入同样多的棋子,它们移动到什么样的位置才能保证平衡?
左边塑料袋所在的刻度
1
1.5
2
2.5
3
3.5
4
右边塑料袋所在的刻度
1
1.5
2
2.5
3
3.5
4
如果塑料袋挂在竹竿左右两边刻度相同的地方,只要两个塑料袋里放相同数量的棋子,竹竿就能保持平衡。
规律总结
如果左右两个塑料袋里放同样多的棋子,要把它们移动到左右刻度相同的地方,竹竿才能保持平衡。
左边的塑料袋放在刻度3上,放4个棋子,右边的塑料袋在刻度4上,放几个棋子才能平衡?
操作得知,放3个棋子才能保证平衡。
观察发现4×3=3×4。
左边的塑料袋在刻度6上放1个棋子,右边的塑料袋在刻度3上放几个呢?
操作得知,放2个棋子才能保证平衡。
发现规律:左边的刻度数×左边所放棋子数=6×1=6,右边的刻度数×右边所放棋子数=3×2=2×3=6。即:左边的刻度数×左边所放棋子数=右边的刻度数×右边所放棋子数。
左边的塑料袋在刻度4上放3个棋子并保持不变,右边的塑料袋分别在各个刻度上放几个棋子才能保证平衡呢?
1.操作过程。
把右边的塑料袋分别放在刻度1、2、3、4、6上,并使竹竿保证平衡,看看分别放了几个棋子。
2.
实验记录如下表:
右刻度
1
2
3
4
6
所放棋子数
12
6
4
3
2
乘积
12
12
12
12
12
要使竹竿平衡,必须满足“左边的刻度数×左边所放棋子数=右边的刻度数×右边所放棋子数”
规律总结
成反比例关系
三、巩固练习
仔细想,认真填。
(1)左边刻度3处挂6个棋子,右边刻度2处应挂( )个棋子才能保持平衡。
(2)左边刻度1处挂4个棋子,现在要在右边挂1个棋子,应挂在刻度( )处才能保持平衡。
(3)要保持平衡,在一侧的刻度数和所挂棋子数乘积一定的情况下,另一侧的刻度数和所挂的棋子数成( )比例关系。
9
4
反
四、课堂小结
活动总结:
1.竹竿平衡的规律(即杠杆原理):当竹竿平衡时,左边的刻度数×左边所放棋子数=右边的刻度数×右边所放棋子数。
2.竹竿平衡,如果“左边的刻度数×左边所放棋子数”的积一定时,右边的刻度数与右边所放棋子数成反比例关系;反之也成立。
整理和复习
第15课时
有趣的平衡
一、新课导入
同学们,你听说过“杠杆原理”吗?
知道它在生活中的应用吗?可能大家
都没有想到,杠杆原理的背后隐藏着
数学原理,那就是反比例关系。
下面就让我们通过实验体验它的奥秘吧。
二、探究新知
准备选一根粗细均匀的竹竿(长约1m),在中点的位置打个孔并栓上绳子,然后从中点开始每隔8cm做一个记号。
①准备的竹竿长度是1m,尽量做到粗细均匀。
②在竹竿中点处打孔栓绳子时注意绳子的长度,同时注意检查拎起绳子后竹竿是否平衡。
③从中点处开始每隔8㎝做一个刻度记号,尽量等距。
④选用的棋子、装棋子的塑料袋要完全一样。
实验条件控制
如果塑料袋挂在竹竿
左右两边刻度相同的
地方,怎样放棋子才
能保证平衡?
左边棋子的个数/个
1
2
3
4
5
6
7
右边棋子的个数/个
1
2
3
4
5
6
7
如果左右两个塑料袋放入同样多的棋子,它们移动到什么样的位置才能保证平衡?
左边塑料袋所在的刻度
1
1.5
2
2.5
3
3.5
4
右边塑料袋所在的刻度
1
1.5
2
2.5
3
3.5
4
如果塑料袋挂在竹竿左右两边刻度相同的地方,只要两个塑料袋里放相同数量的棋子,竹竿就能保持平衡。
规律总结
如果左右两个塑料袋里放同样多的棋子,要把它们移动到左右刻度相同的地方,竹竿才能保持平衡。
左边的塑料袋放在刻度3上,放4个棋子,右边的塑料袋在刻度4上,放几个棋子才能平衡?
操作得知,放3个棋子才能保证平衡。
观察发现4×3=3×4。
左边的塑料袋在刻度6上放1个棋子,右边的塑料袋在刻度3上放几个呢?
操作得知,放2个棋子才能保证平衡。
发现规律:左边的刻度数×左边所放棋子数=6×1=6,右边的刻度数×右边所放棋子数=3×2=2×3=6。即:左边的刻度数×左边所放棋子数=右边的刻度数×右边所放棋子数。
左边的塑料袋在刻度4上放3个棋子并保持不变,右边的塑料袋分别在各个刻度上放几个棋子才能保证平衡呢?
1.操作过程。
把右边的塑料袋分别放在刻度1、2、3、4、6上,并使竹竿保证平衡,看看分别放了几个棋子。
2.
实验记录如下表:
右刻度
1
2
3
4
6
所放棋子数
12
6
4
3
2
乘积
12
12
12
12
12
要使竹竿平衡,必须满足“左边的刻度数×左边所放棋子数=右边的刻度数×右边所放棋子数”
规律总结
成反比例关系
三、巩固练习
仔细想,认真填。
(1)左边刻度3处挂6个棋子,右边刻度2处应挂( )个棋子才能保持平衡。
(2)左边刻度1处挂4个棋子,现在要在右边挂1个棋子,应挂在刻度( )处才能保持平衡。
(3)要保持平衡,在一侧的刻度数和所挂棋子数乘积一定的情况下,另一侧的刻度数和所挂的棋子数成( )比例关系。
9
4
反
四、课堂小结
活动总结:
1.竹竿平衡的规律(即杠杆原理):当竹竿平衡时,左边的刻度数×左边所放棋子数=右边的刻度数×右边所放棋子数。
2.竹竿平衡,如果“左边的刻度数×左边所放棋子数”的积一定时,右边的刻度数与右边所放棋子数成反比例关系;反之也成立。
