六年级数学下册三圆柱和圆锥3.6圆锥的体积教学课件(21张PPT)新人教版
文档属性
| 名称 | 六年级数学下册三圆柱和圆锥3.6圆锥的体积教学课件(21张PPT)新人教版 |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 12:10:28 | ||
图片预览








文档简介
(共21张PPT)
圆柱与圆锥
第5课时
圆锥的认识
一、新课导入
我们已经学会计算圆柱的体积,请你回忆一下如何计算圆柱的体积?
二、探究新知
圆柱的底面是圆,圆锥的底面也是圆……
圆锥的体积和圆柱的体积有没有关系呢?
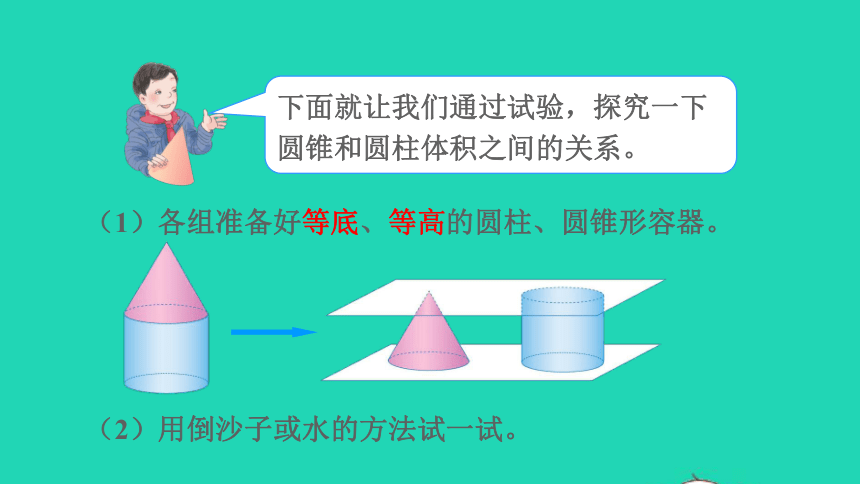
(1)各组准备好等底、等高的圆柱、圆锥形容器。
(2)用倒沙子或水的方法试一试。
下面就让我们通过试验,探究一下圆锥和圆柱体积之间的关系。
(3)通过实验,你发现圆锥的体积与同它等底、等高的圆柱的体积之间的关系了吗?
V
圆锥
=
V
圆柱
=
3
1
3
1
Sh
三次正好倒满。
我把圆柱装满水,再往圆锥里倒。
正好倒了三次。
4m
1.5m
工地上有一堆沙子,近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米沙子重1.5t,这堆沙子大约重多少吨?(得数保留两位小数。)
1.
首先读题,找出已知和未知。
2.
根据已知和未知确定解题步骤并确定每一步要用到的公式。
3.
写出具体的计算过程,每一步写出所用到的公式。
(1)沙堆底面积:S=πr2
6.28×1.5=9.42(t)
(3)沙堆重:
答:这堆沙子大约重9.42吨。
×12.56×1.5=6.28(m?)
3
1
3.14
×(
)=3.14×4=12.56(m2)
2
4
2
(2)沙堆的体积:V=
Sh
3
1
三、巩固练习
1.
一个圆锥形的零件,底面积是19cm2,
高是12cm,这个零件的体积是多少?
答:这个零件的体积是76cm?
。
×19
×12=76(cm?)
3
1
三、巩固练习
2.
一个用钢铸造成的圆锥形铅锤,底面直径是4cm,高5cm。每立方厘米钢大约重7.8g。这个铅锤重多少克?(得数保留整数。)
(2)铅锤的体积:
(1)铅锤底面积:
21×7.8≈164(g)
(3)铅锤的质量:
答:这个铅锤大约重164克
。
×12.56×5≈21(cm3)
3.14×(
)=3.14×4=12.56(cm2)
2
4
2
3
1
三、巩固练习
3.一个圆锥形小麦堆,底面周长是12.56
m,高是1.8
m。如果每立方米小麦约重780
kg,按出粉率80%计算,这堆小麦可磨出多少千克面粉?
12.56÷3.14÷2=2(m)
3.14×22×1.8×
×780×80%=4702.464(kg)
答:这堆小麦可磨出4702.464千克面粉。
四、课堂小结
1.
圆锥的体积等于与它等底等高的圆柱体积的
。
2.
圆锥的体积公式用字母表示为V=
Sh
或V=
πr?h。
3.
当已知圆锥的底面直径和高,可利用公式
V=
π(
)?h来计算圆锥的体积。
圆柱与圆锥
第5课时
圆锥的认识
一、新课导入
我们已经学会计算圆柱的体积,请你回忆一下如何计算圆柱的体积?
二、探究新知
圆柱的底面是圆,圆锥的底面也是圆……
圆锥的体积和圆柱的体积有没有关系呢?
(1)各组准备好等底、等高的圆柱、圆锥形容器。
(2)用倒沙子或水的方法试一试。
下面就让我们通过试验,探究一下圆锥和圆柱体积之间的关系。
(3)通过实验,你发现圆锥的体积与同它等底、等高的圆柱的体积之间的关系了吗?
V
圆锥
=
V
圆柱
=
3
1
3
1
Sh
三次正好倒满。
我把圆柱装满水,再往圆锥里倒。
正好倒了三次。
4m
1.5m
工地上有一堆沙子,近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米沙子重1.5t,这堆沙子大约重多少吨?(得数保留两位小数。)
1.
首先读题,找出已知和未知。
2.
根据已知和未知确定解题步骤并确定每一步要用到的公式。
3.
写出具体的计算过程,每一步写出所用到的公式。
(1)沙堆底面积:S=πr2
6.28×1.5=9.42(t)
(3)沙堆重:
答:这堆沙子大约重9.42吨。
×12.56×1.5=6.28(m?)
3
1
3.14
×(
)=3.14×4=12.56(m2)
2
4
2
(2)沙堆的体积:V=
Sh
3
1
三、巩固练习
1.
一个圆锥形的零件,底面积是19cm2,
高是12cm,这个零件的体积是多少?
答:这个零件的体积是76cm?
。
×19
×12=76(cm?)
3
1
三、巩固练习
2.
一个用钢铸造成的圆锥形铅锤,底面直径是4cm,高5cm。每立方厘米钢大约重7.8g。这个铅锤重多少克?(得数保留整数。)
(2)铅锤的体积:
(1)铅锤底面积:
21×7.8≈164(g)
(3)铅锤的质量:
答:这个铅锤大约重164克
。
×12.56×5≈21(cm3)
3.14×(
)=3.14×4=12.56(cm2)
2
4
2
3
1
三、巩固练习
3.一个圆锥形小麦堆,底面周长是12.56
m,高是1.8
m。如果每立方米小麦约重780
kg,按出粉率80%计算,这堆小麦可磨出多少千克面粉?
12.56÷3.14÷2=2(m)
3.14×22×1.8×
×780×80%=4702.464(kg)
答:这堆小麦可磨出4702.464千克面粉。
四、课堂小结
1.
圆锥的体积等于与它等底等高的圆柱体积的
。
2.
圆锥的体积公式用字母表示为V=
Sh
或V=
πr?h。
3.
当已知圆锥的底面直径和高,可利用公式
V=
π(
)?h来计算圆锥的体积。
