27.3 位似 同步练习(含答案)
图片预览



文档简介
中小学教育资源及组卷应用平台
第27章 相似
27.3 位似
选择题
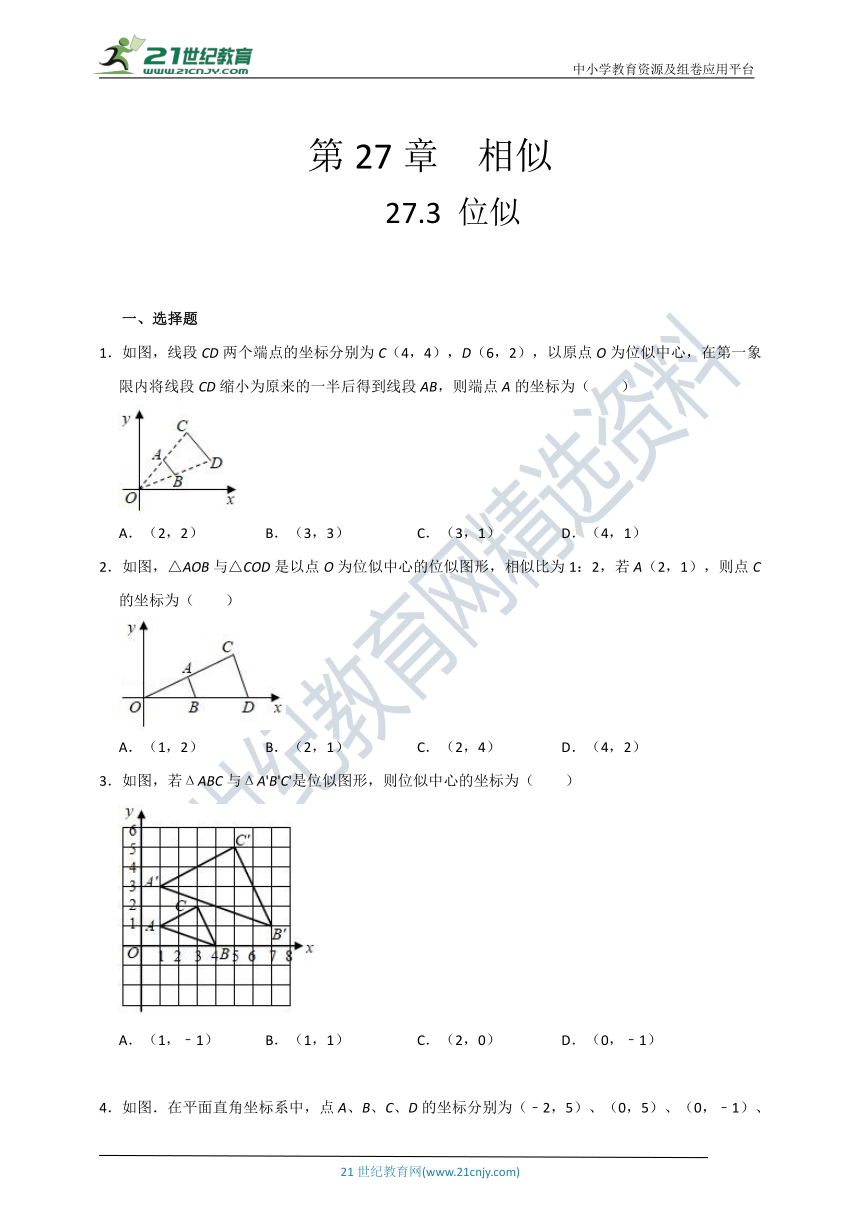
1.如图,线段CD两个端点的坐标分别为C(4,4),D(6,2),以原点O为位似中心,在第一象限内将线段CD缩小为原来的一半后得到线段AB,则端点A的坐标为( )
A.(2,2) B.(3,3) C.(3,1) D.(4,1)
2.如图,△AOB与△COD是以点O为位似中心的位似图形,相似比为1:2,若A(2,1),则点C的坐标为( )
A.(1,2) B.(2,1) C.(2,4) D.(4,2)
3.如图,若ΔABC与ΔA'B'C'是位似图形,则位似中心的坐标为( )
A.(1,﹣1) B.(1,1) C.(2,0) D.(0,﹣1)
4.如图.在平面直角坐标系中,点A、B、C、D的坐标分别为(﹣2,5)、(0,5)、(0,﹣1)、(4,﹣1).若线段AB和CD是位似图形,位似中心在y轴上,则位似中心的坐标为( )
A.(0,1) B.(0,) C.(0,) D.(0,3)
5.等边三角形OAB在平面直角坐标系中的位置如图所示,已知△OAB边长为6,且△OAB与△OA′B′关点O成位似图形,且位似比为1:2,则点A′的坐标可能是( )
A.(﹣6,6) B.(6,6) C.(﹣3,﹣3) D.(6,﹣6)
填空题
6.在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是 .
7.在平面直角坐标系中,△ABC和△A1B1C1的相似比等于,并且是关于原点O的位似图形,若点A的坐标为(3,6),则其对应点A1的坐标是 .
8.如图,已知?ABCD,以B为位似中心,作?ABCD的位似图形?EBFG,位似图形与原图形的位似比为,连结AG,DG.若?ABCD的面积为24,则△ADG的面积为 .
9.在平面直角坐标系中,△ABC的顶点坐标分别是A(6,8),B(7,0),C(7,8)以原点O为位似中心,相似比为,把△ABC缩小,得到△A1B1C1,则点A的对应点A1的坐标为 .
10.如图,在平面直角坐标系中,每个小方格的边长均为1,△AOB与△A′OB′是以原点O为位似中心的位似图形,且位似比为2:1,点A、B都在格点上,则点B′的坐标是 .
解答题
11.如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(﹣3,1),B(﹣1,1),C(0,3).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)画出△ABC以点O为位似中心的位似图形△A2B2C2,△ABC与△A2B2C2的位似比为1:2;
(3)求以B1、B2、A1、A2四个点为顶点构成的四边形的面积.
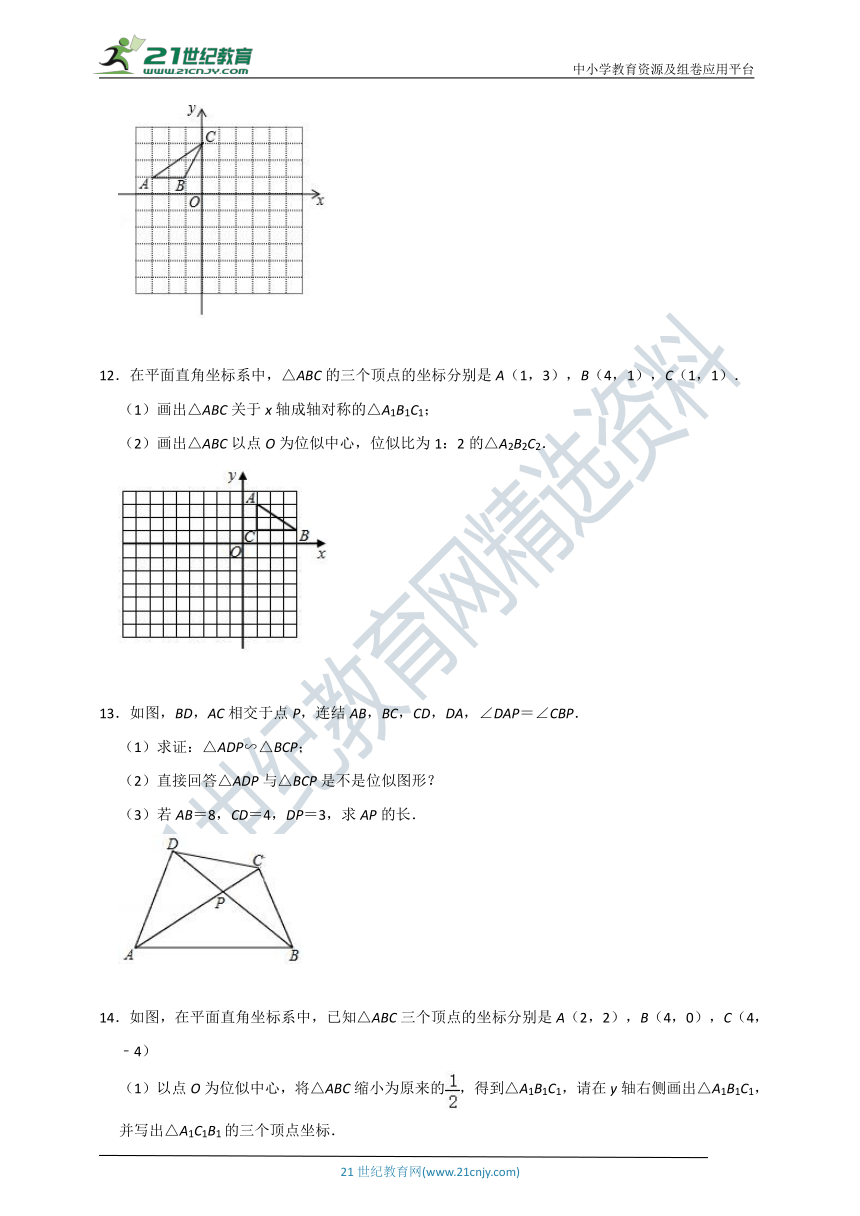
12.在平面直角坐标系中,△ABC的三个顶点的坐标分别是A(1,3),B(4,1),C(1,1).
(1)画出△ABC关于x轴成轴对称的△A1B1C1;
(2)画出△ABC以点O为位似中心,位似比为1:2的△A2B2C2.
13.如图,BD,AC相交于点P,连结AB,BC,CD,DA,∠DAP=∠CBP.
(1)求证:△ADP∽△BCP;
(2)直接回答△ADP与△BCP是不是位似图形?
(3)若AB=8,CD=4,DP=3,求AP的长.
14.如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4)
(1)以点O为位似中心,将△ABC缩小为原来的,得到△A1B1C1,请在y轴右侧画出△A1B1C1,并写出△A1C1B1的三个顶点坐标.
A1 ,B1 ,C1
(2)由已知条件和问题(1),若有一点P(a,b)在△ABC边上,通过(1)中位似变换后的坐标为:.
15.利用位似图形的方法把四边形ABCD放大2倍成四边形A1B1C1D1.
答案
1.A.2.D.3.A.4.D.5.B.
6.【答案】四边形NPMQ.
【解析】解:延长AO、BO、CO、DO分别到Q、P、M、N,
则四边形NPMQ是四边形ABCD的位似图形,
故答案为:四边形NPMQ.
7.【答案】(9,18)或(﹣9,﹣18).
【解析】解:∵△ABC和△A1B1C1的相似比等于,并且是关于原点O的位似图形,点A的坐标为(3,6),
∴点A1的坐标是(3×3,6×3)或(﹣3×3,﹣6×3),即(9,18)或(﹣9,﹣18),
故答案为:(9,18)或(﹣9,﹣18).
8.【答案】4
【解析】解:连接BG,
∵?ABCD和?EBFG是以B为位似中心的位似图形,
∴点D、G、B在同一条直线上,EG∥AD,
∵四边形ABCD是平行四边形,面积为24,
∴△ADB的面积为12,
∵EG∥AD,
∴==,
∴=,
∴△ADG的面积=12×=4,
故答案为:4.
9.【答案】(3,4)或(﹣3,﹣4).
【解析】解:∵以原点O为位似中心,相似比为,把△ABC缩小,得到△A1B1C1,点A的坐标为(6,8),
∴则点A的对应点A′的坐标为(6×,8×)或(﹣6×,﹣8×),即(3,4)或(﹣3,﹣4),
故答案为:(3,4)或(﹣3,﹣4).
10.【答案】(2,﹣2)或(﹣2,2).
【解析】解:△AOB与△A′OB′是以原点O为位似中心的位似图形,位似比为2:1,点B的坐标为(4,﹣4),
∴点B′的坐标为(4×,﹣4×)或(﹣4×,4×),即(2,﹣2)或(﹣2,2),
故答案为:(2,﹣2)或(﹣2,2).
11.【答案】解:(1)如图,△A1B1C1即为所求;
(2)如图,△A2B2C2即为所求;
(3)以B1、B2、A1、A2四个点为顶点构成的四边形的面积为:
(2+4)×3=9.
12.【答案】解:(1)由题意知:△ABC的三个顶点的坐标分别是A(1,3),B(4,1),C(1,1),
则△ABC关于x轴成轴对称的△A1B1C1的坐标为A1(1,﹣3),B1(4,﹣1),C1(1,﹣1),
连接A1C1,A1B1,B1C1
得到△A1B1C1.
如图所示△A1B1C1为所求;
(2)由题意知:位似中心是原点,
则分两种情况:
第一种,△A2B2C2和△ABC在同一侧
则A2(2,6),B2(8,2),C2(2,2),
连接各点,得△A2B2C2.
第二种,△A2B2C2在△ABC的对侧
A2(﹣2,﹣6),B2(﹣8,﹣2),C2(﹣2,﹣2),
连接各点,得△A2B2C2.
因为在网格中作图,图中网格是有范围的,只能在网格中作图,所以位似放大只能能画一个.
综上所述:如图所示△A2B2C2为所求.
13.【答案】(1)证明∵∠DAP=∠CBP,∠DPA=∠CPB,
∴△ADP∽△BCP;
(2)解:△ADP与△BCP不是位似图形,
因为它们的对应点的连线不平行;
(3)解:∵△ADP∽△BCP,
∴=,又∠APB=∠DPC,
∴△APB∽△DPC,
∴=,即=,
解得,AP=6.
14.【答案】 解:
(1)如图即为所求作的△A1B1C1.
根据图形可得:
A1 (1,1)、B1 (2,0)、C1(2,﹣2)
故答案为(1,1)、(2,0)、(2,﹣2).
(2)根据位似比为,可得
P(a,b).
答:点P(a,a)位似变换后的坐标为P(a,).
15.
【答案】解:如图:
_21?????????è?????(www.21cnjy.com)_
第27章 相似
27.3 位似
选择题
1.如图,线段CD两个端点的坐标分别为C(4,4),D(6,2),以原点O为位似中心,在第一象限内将线段CD缩小为原来的一半后得到线段AB,则端点A的坐标为( )
A.(2,2) B.(3,3) C.(3,1) D.(4,1)
2.如图,△AOB与△COD是以点O为位似中心的位似图形,相似比为1:2,若A(2,1),则点C的坐标为( )
A.(1,2) B.(2,1) C.(2,4) D.(4,2)
3.如图,若ΔABC与ΔA'B'C'是位似图形,则位似中心的坐标为( )
A.(1,﹣1) B.(1,1) C.(2,0) D.(0,﹣1)
4.如图.在平面直角坐标系中,点A、B、C、D的坐标分别为(﹣2,5)、(0,5)、(0,﹣1)、(4,﹣1).若线段AB和CD是位似图形,位似中心在y轴上,则位似中心的坐标为( )
A.(0,1) B.(0,) C.(0,) D.(0,3)
5.等边三角形OAB在平面直角坐标系中的位置如图所示,已知△OAB边长为6,且△OAB与△OA′B′关点O成位似图形,且位似比为1:2,则点A′的坐标可能是( )
A.(﹣6,6) B.(6,6) C.(﹣3,﹣3) D.(6,﹣6)
填空题
6.在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是 .
7.在平面直角坐标系中,△ABC和△A1B1C1的相似比等于,并且是关于原点O的位似图形,若点A的坐标为(3,6),则其对应点A1的坐标是 .
8.如图,已知?ABCD,以B为位似中心,作?ABCD的位似图形?EBFG,位似图形与原图形的位似比为,连结AG,DG.若?ABCD的面积为24,则△ADG的面积为 .
9.在平面直角坐标系中,△ABC的顶点坐标分别是A(6,8),B(7,0),C(7,8)以原点O为位似中心,相似比为,把△ABC缩小,得到△A1B1C1,则点A的对应点A1的坐标为 .
10.如图,在平面直角坐标系中,每个小方格的边长均为1,△AOB与△A′OB′是以原点O为位似中心的位似图形,且位似比为2:1,点A、B都在格点上,则点B′的坐标是 .
解答题
11.如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(﹣3,1),B(﹣1,1),C(0,3).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)画出△ABC以点O为位似中心的位似图形△A2B2C2,△ABC与△A2B2C2的位似比为1:2;
(3)求以B1、B2、A1、A2四个点为顶点构成的四边形的面积.
12.在平面直角坐标系中,△ABC的三个顶点的坐标分别是A(1,3),B(4,1),C(1,1).
(1)画出△ABC关于x轴成轴对称的△A1B1C1;
(2)画出△ABC以点O为位似中心,位似比为1:2的△A2B2C2.
13.如图,BD,AC相交于点P,连结AB,BC,CD,DA,∠DAP=∠CBP.
(1)求证:△ADP∽△BCP;
(2)直接回答△ADP与△BCP是不是位似图形?
(3)若AB=8,CD=4,DP=3,求AP的长.
14.如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4)
(1)以点O为位似中心,将△ABC缩小为原来的,得到△A1B1C1,请在y轴右侧画出△A1B1C1,并写出△A1C1B1的三个顶点坐标.
A1 ,B1 ,C1
(2)由已知条件和问题(1),若有一点P(a,b)在△ABC边上,通过(1)中位似变换后的坐标为:.
15.利用位似图形的方法把四边形ABCD放大2倍成四边形A1B1C1D1.
答案
1.A.2.D.3.A.4.D.5.B.
6.【答案】四边形NPMQ.
【解析】解:延长AO、BO、CO、DO分别到Q、P、M、N,
则四边形NPMQ是四边形ABCD的位似图形,
故答案为:四边形NPMQ.
7.【答案】(9,18)或(﹣9,﹣18).
【解析】解:∵△ABC和△A1B1C1的相似比等于,并且是关于原点O的位似图形,点A的坐标为(3,6),
∴点A1的坐标是(3×3,6×3)或(﹣3×3,﹣6×3),即(9,18)或(﹣9,﹣18),
故答案为:(9,18)或(﹣9,﹣18).
8.【答案】4
【解析】解:连接BG,
∵?ABCD和?EBFG是以B为位似中心的位似图形,
∴点D、G、B在同一条直线上,EG∥AD,
∵四边形ABCD是平行四边形,面积为24,
∴△ADB的面积为12,
∵EG∥AD,
∴==,
∴=,
∴△ADG的面积=12×=4,
故答案为:4.
9.【答案】(3,4)或(﹣3,﹣4).
【解析】解:∵以原点O为位似中心,相似比为,把△ABC缩小,得到△A1B1C1,点A的坐标为(6,8),
∴则点A的对应点A′的坐标为(6×,8×)或(﹣6×,﹣8×),即(3,4)或(﹣3,﹣4),
故答案为:(3,4)或(﹣3,﹣4).
10.【答案】(2,﹣2)或(﹣2,2).
【解析】解:△AOB与△A′OB′是以原点O为位似中心的位似图形,位似比为2:1,点B的坐标为(4,﹣4),
∴点B′的坐标为(4×,﹣4×)或(﹣4×,4×),即(2,﹣2)或(﹣2,2),
故答案为:(2,﹣2)或(﹣2,2).
11.【答案】解:(1)如图,△A1B1C1即为所求;
(2)如图,△A2B2C2即为所求;
(3)以B1、B2、A1、A2四个点为顶点构成的四边形的面积为:
(2+4)×3=9.
12.【答案】解:(1)由题意知:△ABC的三个顶点的坐标分别是A(1,3),B(4,1),C(1,1),
则△ABC关于x轴成轴对称的△A1B1C1的坐标为A1(1,﹣3),B1(4,﹣1),C1(1,﹣1),
连接A1C1,A1B1,B1C1
得到△A1B1C1.
如图所示△A1B1C1为所求;
(2)由题意知:位似中心是原点,
则分两种情况:
第一种,△A2B2C2和△ABC在同一侧
则A2(2,6),B2(8,2),C2(2,2),
连接各点,得△A2B2C2.
第二种,△A2B2C2在△ABC的对侧
A2(﹣2,﹣6),B2(﹣8,﹣2),C2(﹣2,﹣2),
连接各点,得△A2B2C2.
因为在网格中作图,图中网格是有范围的,只能在网格中作图,所以位似放大只能能画一个.
综上所述:如图所示△A2B2C2为所求.
13.【答案】(1)证明∵∠DAP=∠CBP,∠DPA=∠CPB,
∴△ADP∽△BCP;
(2)解:△ADP与△BCP不是位似图形,
因为它们的对应点的连线不平行;
(3)解:∵△ADP∽△BCP,
∴=,又∠APB=∠DPC,
∴△APB∽△DPC,
∴=,即=,
解得,AP=6.
14.【答案】 解:
(1)如图即为所求作的△A1B1C1.
根据图形可得:
A1 (1,1)、B1 (2,0)、C1(2,﹣2)
故答案为(1,1)、(2,0)、(2,﹣2).
(2)根据位似比为,可得
P(a,b).
答:点P(a,a)位似变换后的坐标为P(a,).
15.
【答案】解:如图:
_21?????????è?????(www.21cnjy.com)_
