北师大版八年级数学上册第一章:勾股定理(共20张ppt)
文档属性
| 名称 | 北师大版八年级数学上册第一章:勾股定理(共20张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 718.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 06:16:59 | ||
图片预览






文档简介
(共20张PPT)
勾股定理
模块一:认识勾股定理
?
C
A
B
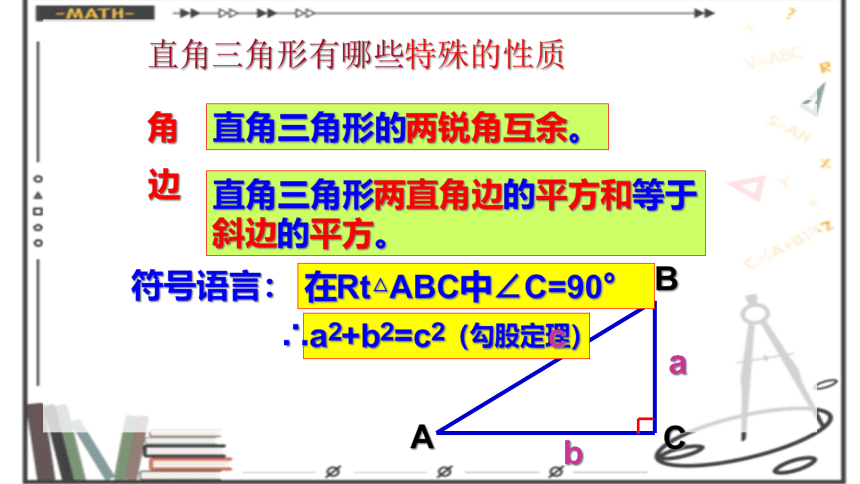
直角三角形有哪些特殊的性质
角
边
直角三角形的两锐角互余。
直角三角形两直角边的平方和等于
斜边的平方。
符号语言:
在Rt△ABC中∠C=90°
a2+b2=c2(勾股定理)
a
b
c
∴
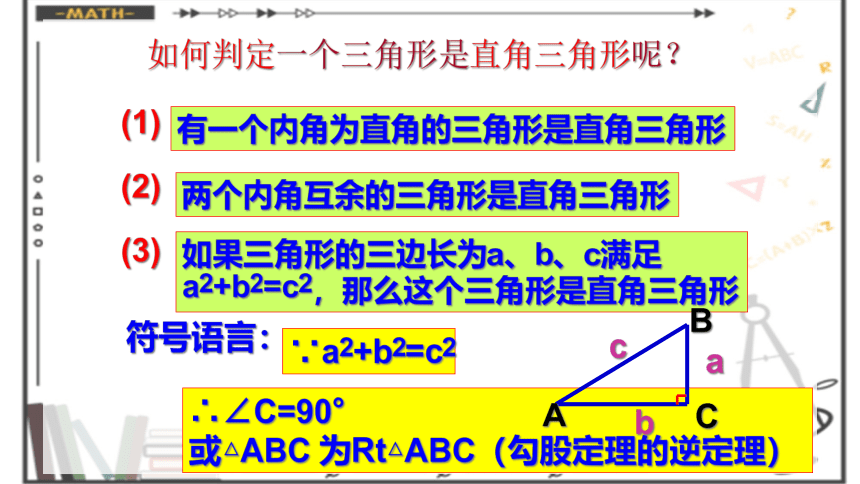
如何判定一个三角形是直角三角形呢?
(1)
(2)
有一个内角为直角的三角形是直角三角形
两个内角互余的三角形是直角三角形
符号语言:
∴∠C=90°
或△ABC
为Rt△ABC(勾股定理的逆定理)
∵a2+b2=c2
(3)
如果三角形的三边长为a、b、c满足
a2+b2=c2,那么这个三角形是直角三角形
C
A
B
a
b
c
第1题
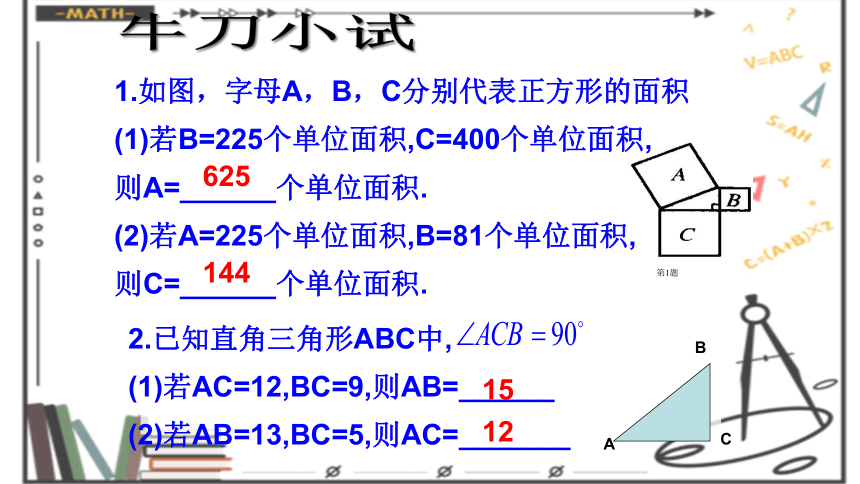
1.如图,字母A,B,C分别代表正方形的面积
(1)若B=225个单位面积,C=400个单位面积,
则A=______个单位面积.
(2)若A=225个单位面积,B=81个单位面积,
则C=______个单位面积.
2.已知直角三角形ABC中,
(1)若AC=12,BC=9,则AB=______
(2)若AB=13,BC=5,则AC=_______
B
A
C
625
144
15
12
牛刀小试
勾股数的妙用:你能速算吗?
3.已知直角三角形中,c是斜边.
(1)a=3,b=4,c=_____
(2)a=6,b=____c=10
(3)a=____,b=40,c=50
(4)a=1.5,b=2,c=________
(5)a=8,b=15,c=________
(6)a=5,b=_______,c=13
(7)a=_____,b=40,c=41
(8)a=7,b=____c=25
你发现了什么?
5
8
30
17
12
9
2.5
24
常见的勾股数:
3、4、5;
5、12、13;
6、8、10;
8、15、17;
9、40、41;
7、24、25.
记一记:(同桌互背)
?
4.有四个三角形,分别满足下列条件:
①一个内角等于另两个内角之和;
②三个角之比为3:4:5;
③三边长分别为7、24、25
④三边之比为5:12:13
其中直角三角形有(
)
A、1个
B、2个
C、3个
D、4个
C
6.若有两条线段分别为3,4,第三条线段为________时,才能组成一个直角三角形
5.下列不是一组勾股数的是(
)
A、5、12、13
B、1.5、2、2.5
C、12、16、20
D、
7、24、25
B
5
或
5
4
3
2
1
观察下列图形,正方形1的边长为7,则
正方形2、3、4、5的面积之和为多少?
规律:
S2+S3+S4+S5=
S1
勾股定理的应用:构建直角三角形
1.在一棵树的20米的B处有两只猴子,其中一只猴子爬下树走到离树40米的A处,另一只爬到树顶D后直接约向A处,且测得AD为50米,求BD的长.
?你
A
D
B
C
模块二:利用勾股定理求线段长度
利用等面积法求直角三角形斜边上的高
例:如图,在Rt△ABC中,AD⊥BC于点D,且AC=12,AB=5,求AD的长。
?
?
A
B
D
C
变式:如图,在△ABC中,AD⊥BC于点D,且AC+AD=32,BD=5,CD=16,求AB的长。
如图,盒内长,宽,高分别是30米,24米和18米,盒内可放的棍子最长是多少米?
18
30
24
你发现什么规律了?
已知:如图,△ABC的周长是24,∠C=90°,且
b=6,则三角形的面积是多少?
A
B
C
a
b
c
解:
∵周长是24,且b=6
∴a+c=24-6=18
设a=x,则c=18-x
∵
∠C=90°,
∴a2+b2=c2
∴x2+62=(18-x)2
解得:x=8
问:已知Rt△ABC中,∠C=90°,若a+b=14cm,c=10cm,则Rt△ABC的面积是(
)
A.24cm2
B.36cm2
C.48cm2
D.60cm2
C
A
B
a
b
c
A
问题一:如图,在矩形ABCD中,BC=8,CD=4,将矩形沿BD折叠,点A落在A′处,求重叠部分△BFD的面积。
A
B
C
D
F
A′
4
8
x
8-x
3
5
模块二:利用勾股定理解决翻折问题
归纳:
折叠出对称,勾股建方程!
变式、如图,在直角三角形ABC中,∠C=90°,BC=3cm,AC=4cm,折叠∠CBA,使BC边落在AB边上,点C落在点E处,求CD的长。
B
C
A
D
E
勾股定理
模块一:认识勾股定理
?
C
A
B
直角三角形有哪些特殊的性质
角
边
直角三角形的两锐角互余。
直角三角形两直角边的平方和等于
斜边的平方。
符号语言:
在Rt△ABC中∠C=90°
a2+b2=c2(勾股定理)
a
b
c
∴
如何判定一个三角形是直角三角形呢?
(1)
(2)
有一个内角为直角的三角形是直角三角形
两个内角互余的三角形是直角三角形
符号语言:
∴∠C=90°
或△ABC
为Rt△ABC(勾股定理的逆定理)
∵a2+b2=c2
(3)
如果三角形的三边长为a、b、c满足
a2+b2=c2,那么这个三角形是直角三角形
C
A
B
a
b
c
第1题
1.如图,字母A,B,C分别代表正方形的面积
(1)若B=225个单位面积,C=400个单位面积,
则A=______个单位面积.
(2)若A=225个单位面积,B=81个单位面积,
则C=______个单位面积.
2.已知直角三角形ABC中,
(1)若AC=12,BC=9,则AB=______
(2)若AB=13,BC=5,则AC=_______
B
A
C
625
144
15
12
牛刀小试
勾股数的妙用:你能速算吗?
3.已知直角三角形中,c是斜边.
(1)a=3,b=4,c=_____
(2)a=6,b=____c=10
(3)a=____,b=40,c=50
(4)a=1.5,b=2,c=________
(5)a=8,b=15,c=________
(6)a=5,b=_______,c=13
(7)a=_____,b=40,c=41
(8)a=7,b=____c=25
你发现了什么?
5
8
30
17
12
9
2.5
24
常见的勾股数:
3、4、5;
5、12、13;
6、8、10;
8、15、17;
9、40、41;
7、24、25.
记一记:(同桌互背)
?
4.有四个三角形,分别满足下列条件:
①一个内角等于另两个内角之和;
②三个角之比为3:4:5;
③三边长分别为7、24、25
④三边之比为5:12:13
其中直角三角形有(
)
A、1个
B、2个
C、3个
D、4个
C
6.若有两条线段分别为3,4,第三条线段为________时,才能组成一个直角三角形
5.下列不是一组勾股数的是(
)
A、5、12、13
B、1.5、2、2.5
C、12、16、20
D、
7、24、25
B
5
或
5
4
3
2
1
观察下列图形,正方形1的边长为7,则
正方形2、3、4、5的面积之和为多少?
规律:
S2+S3+S4+S5=
S1
勾股定理的应用:构建直角三角形
1.在一棵树的20米的B处有两只猴子,其中一只猴子爬下树走到离树40米的A处,另一只爬到树顶D后直接约向A处,且测得AD为50米,求BD的长.
?你
A
D
B
C
模块二:利用勾股定理求线段长度
利用等面积法求直角三角形斜边上的高
例:如图,在Rt△ABC中,AD⊥BC于点D,且AC=12,AB=5,求AD的长。
?
?
A
B
D
C
变式:如图,在△ABC中,AD⊥BC于点D,且AC+AD=32,BD=5,CD=16,求AB的长。
如图,盒内长,宽,高分别是30米,24米和18米,盒内可放的棍子最长是多少米?
18
30
24
你发现什么规律了?
已知:如图,△ABC的周长是24,∠C=90°,且
b=6,则三角形的面积是多少?
A
B
C
a
b
c
解:
∵周长是24,且b=6
∴a+c=24-6=18
设a=x,则c=18-x
∵
∠C=90°,
∴a2+b2=c2
∴x2+62=(18-x)2
解得:x=8
问:已知Rt△ABC中,∠C=90°,若a+b=14cm,c=10cm,则Rt△ABC的面积是(
)
A.24cm2
B.36cm2
C.48cm2
D.60cm2
C
A
B
a
b
c
A
问题一:如图,在矩形ABCD中,BC=8,CD=4,将矩形沿BD折叠,点A落在A′处,求重叠部分△BFD的面积。
A
B
C
D
F
A′
4
8
x
8-x
3
5
模块二:利用勾股定理解决翻折问题
归纳:
折叠出对称,勾股建方程!
变式、如图,在直角三角形ABC中,∠C=90°,BC=3cm,AC=4cm,折叠∠CBA,使BC边落在AB边上,点C落在点E处,求CD的长。
B
C
A
D
E
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
