27.2.3 相似三角形应用举例 同步练习(含答案)
文档属性
| 名称 | 27.2.3 相似三角形应用举例 同步练习(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第27章 相似
27.2.3 相似三角形应用举例
选择题
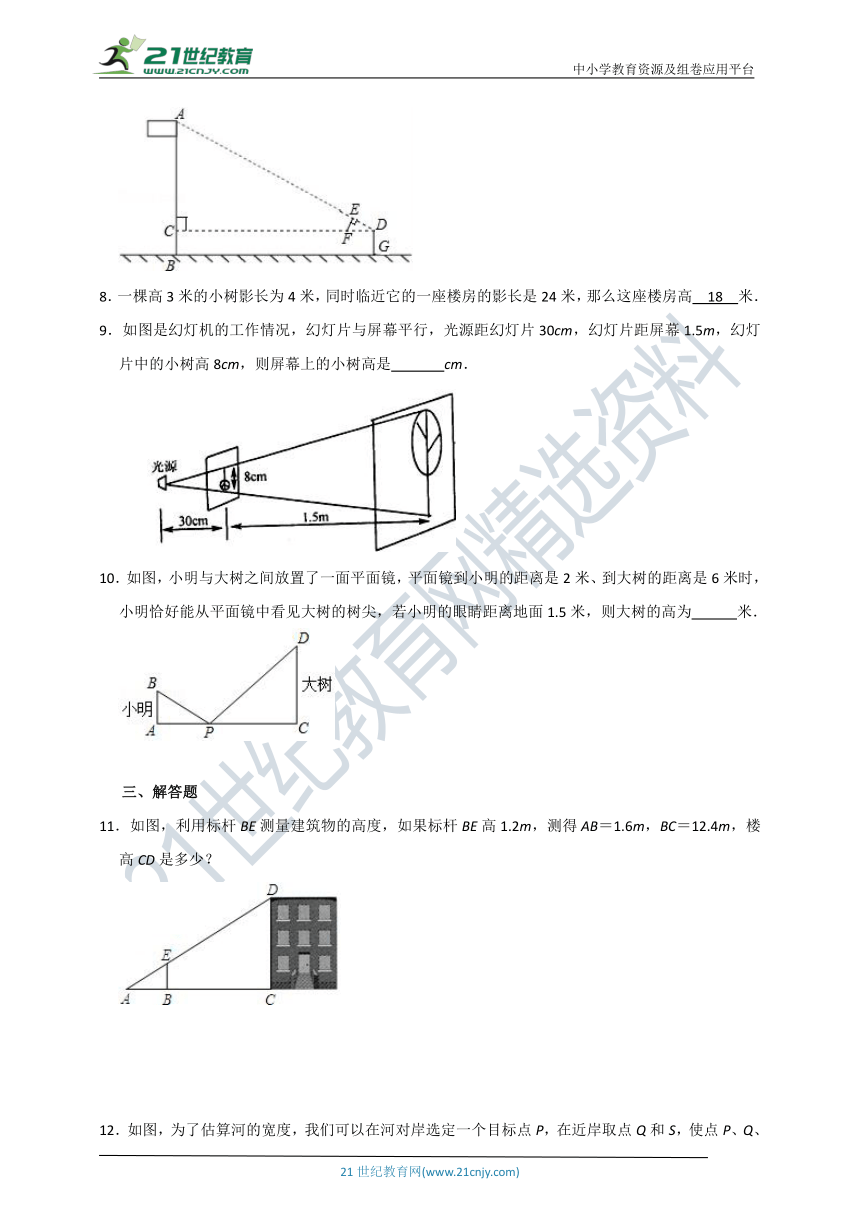
1.如图是圆桌正上方的灯泡(看做一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图,已知桌面的直径为1.2m,桌面距离地面1m.若灯泡距离地面3m,则地面上阴影部分的面积为( )
A.0.36πm2 B.0.81πm2 C.2πm2 D.3.24πm2
2.如图,一同学在湖边看到一棵树,他目测出自己与树的距离为20m,树的顶端在水中的倒影距自己5m远,该同学的身高为1.7m,则树高为( )m.
A.3.4 B.5.1 C.6.8 D.8.5
3.如图,为估算学校的旗杆的高度,身高1.6米的小红同学沿着旗杆在地面的影子AB由A向B走去,当她走到点C处时,她的影子的顶端正好与旗杆的影子的顶端重合,此时测得AC=2m,BC=8m,则旗杆的高度是( )
A.6.4m B.7m C.8m D.9m
4.如图所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行.张强扛着箱子(人与箱子的总高度约为2.2m)乘电梯刚好安全通过,请你根据图中数据回答,两层楼之间的高约为( )
A.5.5m B.6.2m C.11m D.2.2m
5.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条边DF=50cm,EF=30cm,测得边DF离地面的高度AC=1.5m,CD=20m,则树高AB为( )
A.12 m B.13.5 m C.15 m D.16.5 m
填空题
6.如图,身高1.8米的小石从一盏路灯下B处向前走了8米到达点C处时,发现自己在地面上的影子CE长是2米,则路灯的高AB为 米.
7.如图,某校数学兴趣小组利用自制的直角三角形小硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,则旗杆的高度为 米.
8.一棵高3米的小树影长为4米,同时临近它的一座楼房的影长是24米,那么这座楼房高 18 米.
9.如图是幻灯机的工作情况,幻灯片与屏幕平行,光源距幻灯片30cm,幻灯片距屏幕1.5m,幻灯片中的小树高8cm,则屏幕上的小树高是 cm.
10.如图,小明与大树之间放置了一面平面镜,平面镜到小明的距离是2米、到大树的距离是6米时,小明恰好能从平面镜中看见大树的树尖,若小明的眼睛距离地面1.5米,则大树的高为 米.
解答题
11.如图,利用标杆BE测量建筑物的高度,如果标杆BE高1.2m,测得AB=1.6m,BC=12.4m,楼高CD是多少?
12.如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着再过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m,ST=90m,QR=60m,求河的宽度PQ.
13.如图,平台AB上有一棵直立的大树CD,平台的边缘B处有一棵直立的小树BE,平台边缘B外有一个向下的斜坡BG.小明想利用数学课上学习的知识测量大树CD的高度.一天,他发现大树的影子一部分落在平台CB上,一部分落在斜坡上,而且大树的顶端D与小树顶端E的影子恰好重合,且都落在斜坡上的F处,经测量,CB长5米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度(结果保留一位小数).
14.如图,为了计算河两岸间的宽度,我们在河对岸的岸边选定一个目标作为点A,再在河岸的这一边选点B和点C,使AB⊥BC,然后再选点E,使EC⊥BC,BC与AE的交点为D.测得BD=120米,DC=60米,EC=50米,请求出两岸之间AB的距离.
15.如图,某测量人员的眼睛A与标杆顶端F、电视塔顶端E在同一条直线上,已知此人的眼睛到地面的距离AB=1.6m,标杆FC=2.2m,且BC=1m,CD=5m,标杆FC、ED垂直于地面.求电视塔的高ED.
答案
1.B 2.B. 3.C. 4.A 5.D
6.【答案】9
【解析】解:由题意知,CE=2米,CD=1.8米,BC=8米,CD∥AB,
则BE=BC+CE=10米,
∵CD∥AB,
∴△ECD∽△EBA
∴=,即=,
解得AB=9(米),
即路灯的高AB为9米;
故答案为:9.
7.【答案】11.5
【解析】解:由题意得:∠DEF=∠DCA=90°,∠EDF=∠CDA,
∴△DEF∽△DCA,
则,即,
解得:AC=10,
故AB=AC+BC=10+1.5=11.5(m),
即旗杆的高度为11.5m;
故答案为:11.5.
8.【答案】18
【解析】解:∵在同一时刻物高与影长成正比例
∴3:4=楼房的高度:24
∴楼房的高度为18米;
故答案为:18.
9.【答案】48
【解析】解:∵DE∥BC,
∴△AED∽△ABC
∴=
设屏幕上的小树高是x,则=
解得x=48cm.
10.【答案】4.5.
【解析】解:根据题意可得:AB=1.5,AP=2,CP=6,∠BPA=∠DPC,∠A=∠C=90°,
∴△ABP∽△CDP,
∴=,
即:=,
∴AB=4.5(米),
故答案为:
11.【答案】解:∵EB⊥AC,DC⊥AC,
∴EB∥DC,
∴△ABE∽△ACD,
∴=,
∵BE=1.2,AB=1.6,BC=12.4,
∴AC=14,
∴=,
∴CD=10.5.
答:楼高CD是10.5m.
12.【答案】解:根据题意得出:QR∥ST,
则△PQR∽△PST,
故=,
∵QS=45m,ST=90m,QR=60m,
∴=,
解得:PQ=90(m),
∴河的宽度为90米.
13.【答案】 解:延长CB交EF于点H,过点F作FM⊥EB的延长线于点M
∵∠ABG=150°,BE⊥CB
∴∠MBF=150°﹣90°=60°
∴∠MFB=30°
∵BF的长为2米,
∴BM=1米,MF=米
∵BE⊥CB,MF⊥BE
∴BH∥MF
∴△EBH∽△EMF
∴=
又∵EB=1.8米
∴=
∴BH=
∵BE∥CD
∴△HBE∽△HCD
∴=
∵CB=5
∴=
∴CD=15.8米
∴大树CD的高度为15.8米.
14.【答案】解:∵AB⊥BC,EC⊥BC,
∴∠ABC=∠BCE=90°,
∵∠ADB=∠CDE,
∴△ABD∽△ECD,
∴=,
即:=,
解得AB=100.
答:两岸之间AB的距离为100米.
15.【答案】解:作AH⊥ED交FC于点G;如图所示:
∵FC⊥BD,ED⊥BD,AH⊥ED交FC于点G,
∴FG∥EH,
∵AH⊥ED,BD⊥ED,AB⊥BC,ED⊥BC,
∴AH=BD,AG=BC,
∵AB=1.6,FC=2.2,BC=1,CD=5,
∴FG=2.2﹣1.6=0.6,BD=6,
∵FG∥EH,
∴,
解得:EH=3.6,
∴ED=3.6+1.6=5.2(m)
答:电视塔的高ED是5.2米.
_21?????????è?????(www.21cnjy.com)_
第27章 相似
27.2.3 相似三角形应用举例
选择题
1.如图是圆桌正上方的灯泡(看做一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图,已知桌面的直径为1.2m,桌面距离地面1m.若灯泡距离地面3m,则地面上阴影部分的面积为( )
A.0.36πm2 B.0.81πm2 C.2πm2 D.3.24πm2
2.如图,一同学在湖边看到一棵树,他目测出自己与树的距离为20m,树的顶端在水中的倒影距自己5m远,该同学的身高为1.7m,则树高为( )m.
A.3.4 B.5.1 C.6.8 D.8.5
3.如图,为估算学校的旗杆的高度,身高1.6米的小红同学沿着旗杆在地面的影子AB由A向B走去,当她走到点C处时,她的影子的顶端正好与旗杆的影子的顶端重合,此时测得AC=2m,BC=8m,则旗杆的高度是( )
A.6.4m B.7m C.8m D.9m
4.如图所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行.张强扛着箱子(人与箱子的总高度约为2.2m)乘电梯刚好安全通过,请你根据图中数据回答,两层楼之间的高约为( )
A.5.5m B.6.2m C.11m D.2.2m
5.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条边DF=50cm,EF=30cm,测得边DF离地面的高度AC=1.5m,CD=20m,则树高AB为( )
A.12 m B.13.5 m C.15 m D.16.5 m
填空题
6.如图,身高1.8米的小石从一盏路灯下B处向前走了8米到达点C处时,发现自己在地面上的影子CE长是2米,则路灯的高AB为 米.
7.如图,某校数学兴趣小组利用自制的直角三角形小硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,则旗杆的高度为 米.
8.一棵高3米的小树影长为4米,同时临近它的一座楼房的影长是24米,那么这座楼房高 18 米.
9.如图是幻灯机的工作情况,幻灯片与屏幕平行,光源距幻灯片30cm,幻灯片距屏幕1.5m,幻灯片中的小树高8cm,则屏幕上的小树高是 cm.
10.如图,小明与大树之间放置了一面平面镜,平面镜到小明的距离是2米、到大树的距离是6米时,小明恰好能从平面镜中看见大树的树尖,若小明的眼睛距离地面1.5米,则大树的高为 米.
解答题
11.如图,利用标杆BE测量建筑物的高度,如果标杆BE高1.2m,测得AB=1.6m,BC=12.4m,楼高CD是多少?
12.如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着再过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m,ST=90m,QR=60m,求河的宽度PQ.
13.如图,平台AB上有一棵直立的大树CD,平台的边缘B处有一棵直立的小树BE,平台边缘B外有一个向下的斜坡BG.小明想利用数学课上学习的知识测量大树CD的高度.一天,他发现大树的影子一部分落在平台CB上,一部分落在斜坡上,而且大树的顶端D与小树顶端E的影子恰好重合,且都落在斜坡上的F处,经测量,CB长5米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度(结果保留一位小数).
14.如图,为了计算河两岸间的宽度,我们在河对岸的岸边选定一个目标作为点A,再在河岸的这一边选点B和点C,使AB⊥BC,然后再选点E,使EC⊥BC,BC与AE的交点为D.测得BD=120米,DC=60米,EC=50米,请求出两岸之间AB的距离.
15.如图,某测量人员的眼睛A与标杆顶端F、电视塔顶端E在同一条直线上,已知此人的眼睛到地面的距离AB=1.6m,标杆FC=2.2m,且BC=1m,CD=5m,标杆FC、ED垂直于地面.求电视塔的高ED.
答案
1.B 2.B. 3.C. 4.A 5.D
6.【答案】9
【解析】解:由题意知,CE=2米,CD=1.8米,BC=8米,CD∥AB,
则BE=BC+CE=10米,
∵CD∥AB,
∴△ECD∽△EBA
∴=,即=,
解得AB=9(米),
即路灯的高AB为9米;
故答案为:9.
7.【答案】11.5
【解析】解:由题意得:∠DEF=∠DCA=90°,∠EDF=∠CDA,
∴△DEF∽△DCA,
则,即,
解得:AC=10,
故AB=AC+BC=10+1.5=11.5(m),
即旗杆的高度为11.5m;
故答案为:11.5.
8.【答案】18
【解析】解:∵在同一时刻物高与影长成正比例
∴3:4=楼房的高度:24
∴楼房的高度为18米;
故答案为:18.
9.【答案】48
【解析】解:∵DE∥BC,
∴△AED∽△ABC
∴=
设屏幕上的小树高是x,则=
解得x=48cm.
10.【答案】4.5.
【解析】解:根据题意可得:AB=1.5,AP=2,CP=6,∠BPA=∠DPC,∠A=∠C=90°,
∴△ABP∽△CDP,
∴=,
即:=,
∴AB=4.5(米),
故答案为:
11.【答案】解:∵EB⊥AC,DC⊥AC,
∴EB∥DC,
∴△ABE∽△ACD,
∴=,
∵BE=1.2,AB=1.6,BC=12.4,
∴AC=14,
∴=,
∴CD=10.5.
答:楼高CD是10.5m.
12.【答案】解:根据题意得出:QR∥ST,
则△PQR∽△PST,
故=,
∵QS=45m,ST=90m,QR=60m,
∴=,
解得:PQ=90(m),
∴河的宽度为90米.
13.【答案】 解:延长CB交EF于点H,过点F作FM⊥EB的延长线于点M
∵∠ABG=150°,BE⊥CB
∴∠MBF=150°﹣90°=60°
∴∠MFB=30°
∵BF的长为2米,
∴BM=1米,MF=米
∵BE⊥CB,MF⊥BE
∴BH∥MF
∴△EBH∽△EMF
∴=
又∵EB=1.8米
∴=
∴BH=
∵BE∥CD
∴△HBE∽△HCD
∴=
∵CB=5
∴=
∴CD=15.8米
∴大树CD的高度为15.8米.
14.【答案】解:∵AB⊥BC,EC⊥BC,
∴∠ABC=∠BCE=90°,
∵∠ADB=∠CDE,
∴△ABD∽△ECD,
∴=,
即:=,
解得AB=100.
答:两岸之间AB的距离为100米.
15.【答案】解:作AH⊥ED交FC于点G;如图所示:
∵FC⊥BD,ED⊥BD,AH⊥ED交FC于点G,
∴FG∥EH,
∵AH⊥ED,BD⊥ED,AB⊥BC,ED⊥BC,
∴AH=BD,AG=BC,
∵AB=1.6,FC=2.2,BC=1,CD=5,
∴FG=2.2﹣1.6=0.6,BD=6,
∵FG∥EH,
∴,
解得:EH=3.6,
∴ED=3.6+1.6=5.2(m)
答:电视塔的高ED是5.2米.
_21?????????è?????(www.21cnjy.com)_
