人教版 九年级数学 第21章 一元二次方程 复习题(word版含答案)
文档属性
| 名称 | 人教版 九年级数学 第21章 一元二次方程 复习题(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 79.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 12:28:29 | ||
图片预览



文档简介
人教版
九年级数学
第21章
一元二次方程
复习题
一、选择题(本大题共10道小题)
1.
一元二次方程x(x-2)=2-x的根是( )
A.
-1
B.
2
C.
1和2
D.
-1和2
2.
用配方法将方程x2+4x-4=0化成(x+m)2=n的形式,则m,n的值分别是( )
A.-2,0
B.2,0
C.-2,8
D.2,8
3.
某景点的参观人数逐年增加,据统计,2014年为10.8万人次,2016年为16.8万人次.设参观人次的平均年增长率为x,则( )
A.
10.8(1+x)=16.8
B.
16.8(1-x)=10.8
C.
10.8(1+x)2=16.8
D.
10.8[(1+x)+(1+x)2]=16.8
4.
若关于x的一元二次方程(k-1)x2+x+1=0有两个实数根,则k的取值范围是( )
A.k≤
B.k>
C.k<且k≠1
D.k≤且k≠1
5.
已知直角三角形的两条直角边长恰好是方程x2-5x+6=0的两个根,则此直角三角形的斜边长是( )
A.
B.
C.13
D.5
6.
代数式x2-4x-2020的最小值是( )
A.-2018
B.-2020
C.-2022
D.-2024
7.
以x=为根的一元二次方程可能是( )
A.x2+bx+c=0
B.x2+bx-c=0
C.x2-bx+c=0
D.x2-bx-c=0
8.
能说明命题“关于x的方程x2-4x+m=0一定有实数根”是假命题的反例为( )
A.m=-1
B.m=0
C.m=4
D.m=5
9.
某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为扩大销售,尽快减少库存,商场决定釆取降价措施.调查发现,每件衬衫每降价1元,平均每天可多售出2件,若商场每天要盈利1200元,则每件衬衫应降价( )
A.5元
B.10元
C.20元
D.10元或20元
10.
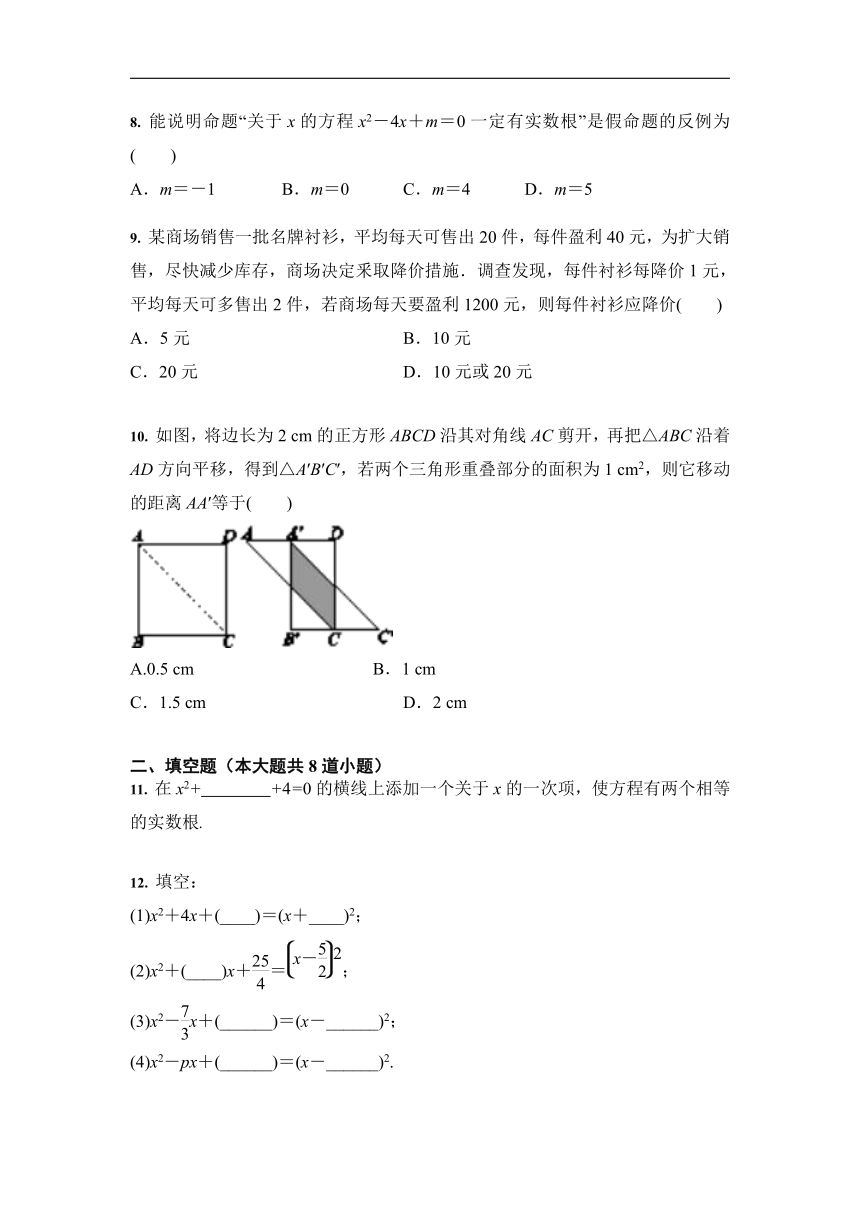
如图,将边长为2
cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1
cm2,则它移动的距离AA′等于( )
A.0.5
cm
B.1
cm
C.1.5
cm
D.2
cm
二、填空题(本大题共8道小题)
11.
在x2+ +4=0的横线上添加一个关于x的一次项,使方程有两个相等的实数根.?
12.
填空:
(1)x2+4x+(____)=(x+____)2;
(2)x2+(____)x+=;
(3)x2-x+(______)=(x-______)2;
(4)x2-px+(______)=(x-______)2.
13.
某中学要组织一次篮球比赛,以班为单位,赛制为单循环形式(每两班之间都赛一场),现计划安排15场比赛,则共有多少个班级参赛?设共有x个班级参赛,根据题意,可列方程为______________.
14.
配方法解一元二次方程x2-2
x+1=0,所得结果是x1=________,x2=________.
15.
根据下表中的数据写出方程x2+3x-4=0的一个根为________.
16.
2019·成都
已知x1,x2是关于x的一元二次方程x2+2x+k-1=0的两个实数根,且x12+x22-x1x2=13,则k的值为________.
17.
已知关于x的一元二次方程(k-1)x2-2x+1=0有两个不相等的实数根,则k的最大整数值为________.
18.
已知关于x的方程ax2-bx+c=0(a≠0)的一个根是,且b2-4ac=0,则此方程的另一个根是________.
三、解答题(本大题共4道小题)
19.
2019·呼和浩特
用配方法求一元二次方程(2x+3)(x-6)=16的实数根.
20.
已知多项式乘法:(x+a)(x+b)=x2+(a+b)x+ab,将该式从右到左使用,即可得到“十字相乘法”进行因式分解的公式:
x2+(a+b)x+ab=(x+a)(x+b).
示例 分解因式:x2+5x+6=x2+(2+3)x+2×3=(x+2)(x+3).
(1)尝试 分解因式:x2+6x+8=(x+________)·(x+________);
(2)应用 请用上述方法解方程:x2-3x-4=0.
21.
2019·黄石
已知关于x的一元二次方程x2-6x+(4m+1)=0有实数根.
(1)求m的取值范围;
(2)若该方程的两个实数根为x1,x2,且|x1-x2|=4,求m的值.
22.
某网店销售台灯,成本为每个30元.销售大数据分析表明:当每个台灯的售价为40元时,平均每月售出600个;若每个台灯的售价每下降1元,其月销售量就增加200个.
(1)若每个台灯的售价下降1元,则每月能售出________个台灯;若每个台灯的售价下降x元(x>0),则每月能售出________个台灯.
(2)为迎接“双十一”,该网店决定降价促销,在库存为1210个台灯的情况下,若预计月获利恰好为8400元,求每个台灯的售价.
(3)该网店的月获利能否达到9600元?请说明理由.
人教版
九年级数学
第21章
一元二次方程
复习题-答案
一、选择题(本大题共10道小题)
1.
【答案】D 【解析】x(x-2)=2-x?x(x-2)+(x-2)=0?(x-2)(x+1)=0?x1=2,x2=-1.
2.
【答案】D [解析]
∵x2+4x-4=0,
∴x2+4x=4,
则x2+4x+4=4+4,即(x+2)2=8,
∴m=2,n=8.
3.
【答案】C 【解析】∵设平均年增长率为x,2014年为10.8万人次,则2015年为10.8(1+x)万人次,2016年为10.8(1+x)2万人次,∴根据题意得,10.8(1+x)2=16.8.
4.
【答案】D [解析]
∵关于x的一元二次方程(k-1)x2+x+1=0有两个实数根,
∴Δ≥0,
即12-4×(k-1)×1≥0,
解得k≤.
又∵k-1≠0,
∴k≠1,
∴k的取值范围为k≤且k≠1.
故选D.
5.
【答案】A [解析]
x2-5x+6=0.
左边分解因式,得(x-2)(x-3)=0.
解得x=2或x=3.
即直角三角形的两条直角边长分别为2,3.
根据勾股定理得斜边长为=.
6.
【答案】D [解析]
x2-4x-2020
=x2-4x+4-4-2020
=(x-2)2-2024.
∵(x-2)2≥0,
∴(x-2)2-2024≥-2024,即代数式x2-4x-2020的最小值是-2024.
7.
【答案】D [解析]
对照求根公式,可确定二次项系数、一次项系数和常数项分别为1,-b,-c.故选D.
8.
【答案】D [解析]
方程根的判别式Δ=b2-4ac=(-4)2-4m=16-4m,当Δ<0时,方程无实数根,∴当16-4m<0,即m>4时,原方程无实数根,四个选项中,只有m=5符合条件.故选D.
9.
【答案】C [解析]
设每件衬衫降价x元,则每天可售出(20+2x)件,
根据题意,得(40-x)(20+2x)=1200,解得x1=10,x2=20.
∵要扩大销售,减少库存,∴x=20.
10.
【答案】B [解析]
设AC交A′B′于点H,如图所示.
根据题意易得△A′HA是等腰直角三角形.
设AA′=x
cm,则A′D=(2-x)cm,
∴x·(2-x)=1,
解得x1=x2=1,即AA′=1
cm.
二、填空题(本大题共8道小题)
11.
【答案】4x(或-4x,只写一个即可) [解析]一元二次方程有两个相等的实根,则b2-4ac=b2-16=0,解得b=±4,所以一次项为4x或-4x.
12.
【答案】(1)4 2 (2)-5 (3)
(4)
13.
【答案】x(x-1)=15 [解析]
共有x个班级参赛,每个班都要赛(x-1)场,但每两班之间只有一场比赛,由题意得x(x-1)=15.
14.
【答案】-1 +1
15.
【答案】x=1
16.
【答案】-2 [解析]
根据题意,得x1+x2=-2,x1x2=k-1,
∴x12+x22-x1x2=(x1+x2)2-3x1x2=4-3(k-1)=13,
解得k=-2.
故答案为:-2.
17.
【答案】0 [解析]
由题意得Δ=b2-4ac=4-4(k-1)>0,∴k<2.又∵k-1≠0,即k≠1,∴k<2且k≠1,∴k的最大整数值为0.
18.
【答案】 [解析]
由b2-4ac=0知原方程根的判别式为0,因此原方程有两个相等的实数根.故原方程的另一个根也是.
三、解答题(本大题共4道小题)
19.
【答案】
解:原方程化为一般形式为2x2-9x-34=0,
x2-x=17,
x2-x+=17+,
(x-)2=,
x-=±,
所以x1=,x2=.
20.
【答案】
[解析]
(1)把8分解成2×4,且2+4=6.
(2)把-4分解成1×(-4),
且1+(-4)=-3.
解:(1)2 4
(2)x2-3x-4=0,
(x+1)(x-4)=0,
所以x+1=0或x-4=0.
所以x1=-1,x2=4.
21.
【答案】
解:(1)∵关于x的一元二次方程x2-6x+(4m+1)=0有实数根,
∴Δ=b2-4ac=(-6)2-4×1×(4m+1)≥0,
解得m≤2.
(2)∵方程x2-6x+(4m+1)=0的两个实数根为x1,x2,
∴x1+x2=6,x1x2=4m+1,
∴(x1-x2)2=(x1+x2)2-4x1x2=42,即32-16m=16,
解得m=1.
22.
【答案】
解:(1)800 (600+200x)
(2)设每个台灯的售价为y元.
根据题意,得
(y-30)[(40-y)×200+600]=8400,
解得y1=36,y2=37.
当y=36时,月销售量为(40-36)×200+600=1400(个)>1210个,不合题意,舍去;
当y=37时,月销售量为(40-37)×200+600=1200(个)<1210个,符合题意.
答:每个台灯的售价为37元.
(3)该网店的月获利不能达到9600元.理由如下:
设每个台灯的售价下降a元,则(40-30-a)(600+200a)=9600,
整理,得a2-7a+18=0.
∵Δ=49-72=-23<0,
∴该方程无实数根.
即该网店的月获利不能达到9600元.
九年级数学
第21章
一元二次方程
复习题
一、选择题(本大题共10道小题)
1.
一元二次方程x(x-2)=2-x的根是( )
A.
-1
B.
2
C.
1和2
D.
-1和2
2.
用配方法将方程x2+4x-4=0化成(x+m)2=n的形式,则m,n的值分别是( )
A.-2,0
B.2,0
C.-2,8
D.2,8
3.
某景点的参观人数逐年增加,据统计,2014年为10.8万人次,2016年为16.8万人次.设参观人次的平均年增长率为x,则( )
A.
10.8(1+x)=16.8
B.
16.8(1-x)=10.8
C.
10.8(1+x)2=16.8
D.
10.8[(1+x)+(1+x)2]=16.8
4.
若关于x的一元二次方程(k-1)x2+x+1=0有两个实数根,则k的取值范围是( )
A.k≤
B.k>
C.k<且k≠1
D.k≤且k≠1
5.
已知直角三角形的两条直角边长恰好是方程x2-5x+6=0的两个根,则此直角三角形的斜边长是( )
A.
B.
C.13
D.5
6.
代数式x2-4x-2020的最小值是( )
A.-2018
B.-2020
C.-2022
D.-2024
7.
以x=为根的一元二次方程可能是( )
A.x2+bx+c=0
B.x2+bx-c=0
C.x2-bx+c=0
D.x2-bx-c=0
8.
能说明命题“关于x的方程x2-4x+m=0一定有实数根”是假命题的反例为( )
A.m=-1
B.m=0
C.m=4
D.m=5
9.
某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为扩大销售,尽快减少库存,商场决定釆取降价措施.调查发现,每件衬衫每降价1元,平均每天可多售出2件,若商场每天要盈利1200元,则每件衬衫应降价( )
A.5元
B.10元
C.20元
D.10元或20元
10.
如图,将边长为2
cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1
cm2,则它移动的距离AA′等于( )
A.0.5
cm
B.1
cm
C.1.5
cm
D.2
cm
二、填空题(本大题共8道小题)
11.
在x2+ +4=0的横线上添加一个关于x的一次项,使方程有两个相等的实数根.?
12.
填空:
(1)x2+4x+(____)=(x+____)2;
(2)x2+(____)x+=;
(3)x2-x+(______)=(x-______)2;
(4)x2-px+(______)=(x-______)2.
13.
某中学要组织一次篮球比赛,以班为单位,赛制为单循环形式(每两班之间都赛一场),现计划安排15场比赛,则共有多少个班级参赛?设共有x个班级参赛,根据题意,可列方程为______________.
14.
配方法解一元二次方程x2-2
x+1=0,所得结果是x1=________,x2=________.
15.
根据下表中的数据写出方程x2+3x-4=0的一个根为________.
16.
2019·成都
已知x1,x2是关于x的一元二次方程x2+2x+k-1=0的两个实数根,且x12+x22-x1x2=13,则k的值为________.
17.
已知关于x的一元二次方程(k-1)x2-2x+1=0有两个不相等的实数根,则k的最大整数值为________.
18.
已知关于x的方程ax2-bx+c=0(a≠0)的一个根是,且b2-4ac=0,则此方程的另一个根是________.
三、解答题(本大题共4道小题)
19.
2019·呼和浩特
用配方法求一元二次方程(2x+3)(x-6)=16的实数根.
20.
已知多项式乘法:(x+a)(x+b)=x2+(a+b)x+ab,将该式从右到左使用,即可得到“十字相乘法”进行因式分解的公式:
x2+(a+b)x+ab=(x+a)(x+b).
示例 分解因式:x2+5x+6=x2+(2+3)x+2×3=(x+2)(x+3).
(1)尝试 分解因式:x2+6x+8=(x+________)·(x+________);
(2)应用 请用上述方法解方程:x2-3x-4=0.
21.
2019·黄石
已知关于x的一元二次方程x2-6x+(4m+1)=0有实数根.
(1)求m的取值范围;
(2)若该方程的两个实数根为x1,x2,且|x1-x2|=4,求m的值.
22.
某网店销售台灯,成本为每个30元.销售大数据分析表明:当每个台灯的售价为40元时,平均每月售出600个;若每个台灯的售价每下降1元,其月销售量就增加200个.
(1)若每个台灯的售价下降1元,则每月能售出________个台灯;若每个台灯的售价下降x元(x>0),则每月能售出________个台灯.
(2)为迎接“双十一”,该网店决定降价促销,在库存为1210个台灯的情况下,若预计月获利恰好为8400元,求每个台灯的售价.
(3)该网店的月获利能否达到9600元?请说明理由.
人教版
九年级数学
第21章
一元二次方程
复习题-答案
一、选择题(本大题共10道小题)
1.
【答案】D 【解析】x(x-2)=2-x?x(x-2)+(x-2)=0?(x-2)(x+1)=0?x1=2,x2=-1.
2.
【答案】D [解析]
∵x2+4x-4=0,
∴x2+4x=4,
则x2+4x+4=4+4,即(x+2)2=8,
∴m=2,n=8.
3.
【答案】C 【解析】∵设平均年增长率为x,2014年为10.8万人次,则2015年为10.8(1+x)万人次,2016年为10.8(1+x)2万人次,∴根据题意得,10.8(1+x)2=16.8.
4.
【答案】D [解析]
∵关于x的一元二次方程(k-1)x2+x+1=0有两个实数根,
∴Δ≥0,
即12-4×(k-1)×1≥0,
解得k≤.
又∵k-1≠0,
∴k≠1,
∴k的取值范围为k≤且k≠1.
故选D.
5.
【答案】A [解析]
x2-5x+6=0.
左边分解因式,得(x-2)(x-3)=0.
解得x=2或x=3.
即直角三角形的两条直角边长分别为2,3.
根据勾股定理得斜边长为=.
6.
【答案】D [解析]
x2-4x-2020
=x2-4x+4-4-2020
=(x-2)2-2024.
∵(x-2)2≥0,
∴(x-2)2-2024≥-2024,即代数式x2-4x-2020的最小值是-2024.
7.
【答案】D [解析]
对照求根公式,可确定二次项系数、一次项系数和常数项分别为1,-b,-c.故选D.
8.
【答案】D [解析]
方程根的判别式Δ=b2-4ac=(-4)2-4m=16-4m,当Δ<0时,方程无实数根,∴当16-4m<0,即m>4时,原方程无实数根,四个选项中,只有m=5符合条件.故选D.
9.
【答案】C [解析]
设每件衬衫降价x元,则每天可售出(20+2x)件,
根据题意,得(40-x)(20+2x)=1200,解得x1=10,x2=20.
∵要扩大销售,减少库存,∴x=20.
10.
【答案】B [解析]
设AC交A′B′于点H,如图所示.
根据题意易得△A′HA是等腰直角三角形.
设AA′=x
cm,则A′D=(2-x)cm,
∴x·(2-x)=1,
解得x1=x2=1,即AA′=1
cm.
二、填空题(本大题共8道小题)
11.
【答案】4x(或-4x,只写一个即可) [解析]一元二次方程有两个相等的实根,则b2-4ac=b2-16=0,解得b=±4,所以一次项为4x或-4x.
12.
【答案】(1)4 2 (2)-5 (3)
(4)
13.
【答案】x(x-1)=15 [解析]
共有x个班级参赛,每个班都要赛(x-1)场,但每两班之间只有一场比赛,由题意得x(x-1)=15.
14.
【答案】-1 +1
15.
【答案】x=1
16.
【答案】-2 [解析]
根据题意,得x1+x2=-2,x1x2=k-1,
∴x12+x22-x1x2=(x1+x2)2-3x1x2=4-3(k-1)=13,
解得k=-2.
故答案为:-2.
17.
【答案】0 [解析]
由题意得Δ=b2-4ac=4-4(k-1)>0,∴k<2.又∵k-1≠0,即k≠1,∴k<2且k≠1,∴k的最大整数值为0.
18.
【答案】 [解析]
由b2-4ac=0知原方程根的判别式为0,因此原方程有两个相等的实数根.故原方程的另一个根也是.
三、解答题(本大题共4道小题)
19.
【答案】
解:原方程化为一般形式为2x2-9x-34=0,
x2-x=17,
x2-x+=17+,
(x-)2=,
x-=±,
所以x1=,x2=.
20.
【答案】
[解析]
(1)把8分解成2×4,且2+4=6.
(2)把-4分解成1×(-4),
且1+(-4)=-3.
解:(1)2 4
(2)x2-3x-4=0,
(x+1)(x-4)=0,
所以x+1=0或x-4=0.
所以x1=-1,x2=4.
21.
【答案】
解:(1)∵关于x的一元二次方程x2-6x+(4m+1)=0有实数根,
∴Δ=b2-4ac=(-6)2-4×1×(4m+1)≥0,
解得m≤2.
(2)∵方程x2-6x+(4m+1)=0的两个实数根为x1,x2,
∴x1+x2=6,x1x2=4m+1,
∴(x1-x2)2=(x1+x2)2-4x1x2=42,即32-16m=16,
解得m=1.
22.
【答案】
解:(1)800 (600+200x)
(2)设每个台灯的售价为y元.
根据题意,得
(y-30)[(40-y)×200+600]=8400,
解得y1=36,y2=37.
当y=36时,月销售量为(40-36)×200+600=1400(个)>1210个,不合题意,舍去;
当y=37时,月销售量为(40-37)×200+600=1200(个)<1210个,符合题意.
答:每个台灯的售价为37元.
(3)该网店的月获利不能达到9600元.理由如下:
设每个台灯的售价下降a元,则(40-30-a)(600+200a)=9600,
整理,得a2-7a+18=0.
∵Δ=49-72=-23<0,
∴该方程无实数根.
即该网店的月获利不能达到9600元.
同课章节目录
