六年级数学下册课件-3.1.3 圆柱的体积1-人教版(共32张PPT)
文档属性
| 名称 | 六年级数学下册课件-3.1.3 圆柱的体积1-人教版(共32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 814.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 11:26:00 | ||
图片预览






文档简介
(共32张PPT)
圆柱的体积
长
高
宽
棱
长
长
v
=a
b
h
v
3
正
=a
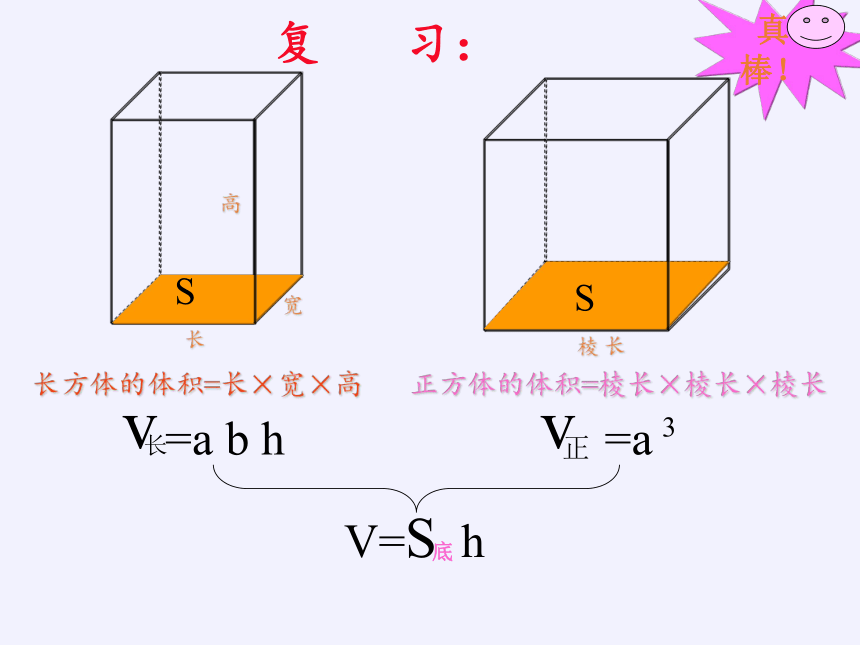
V=S
h
底
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
复
习:
真
棒!
S
S
探究新知
能不能猜想一下圆柱的体积可能与什么有关?到底要怎么研究呢?
你会计算圆柱的体积吗?
探究新知
探究新知
探究新知
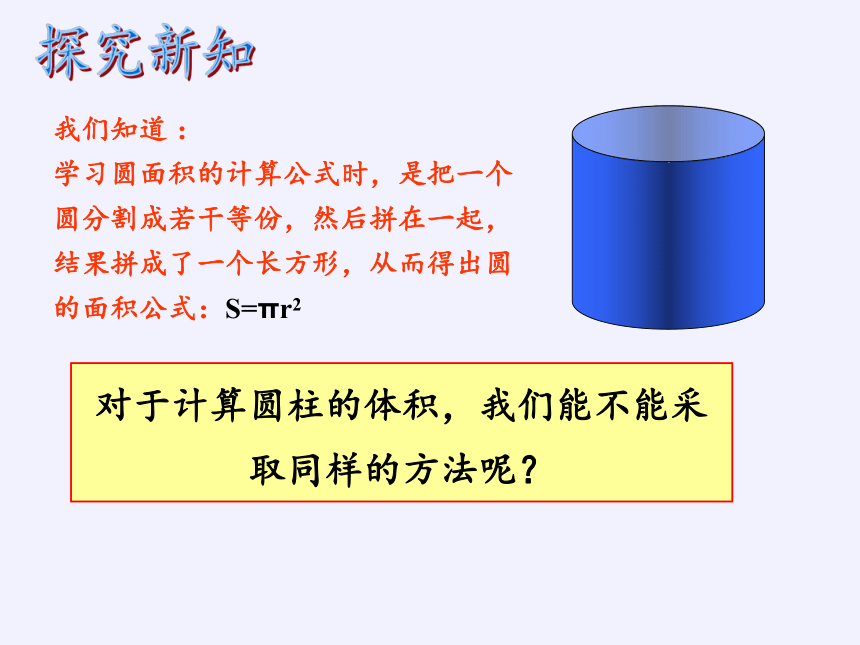
我们知道
:
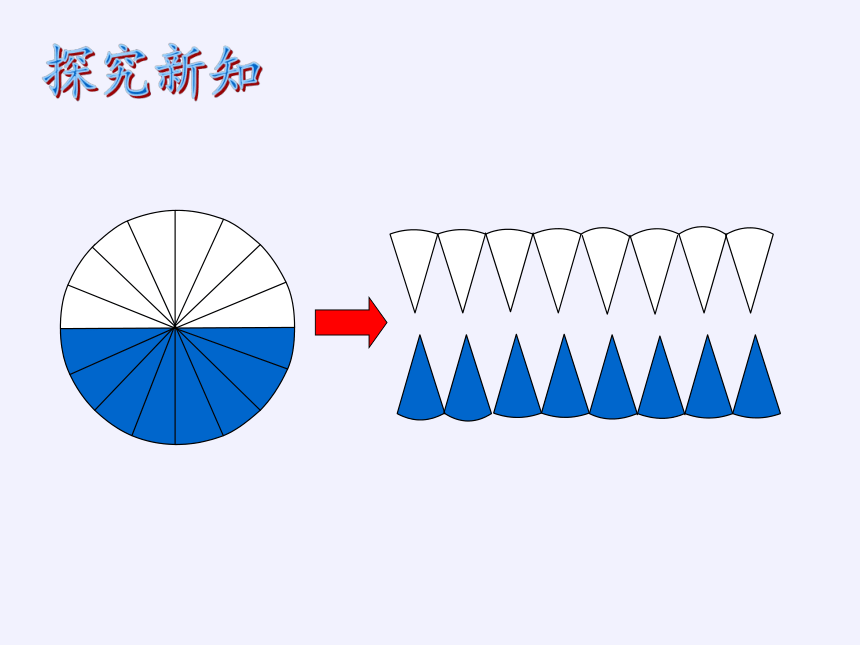
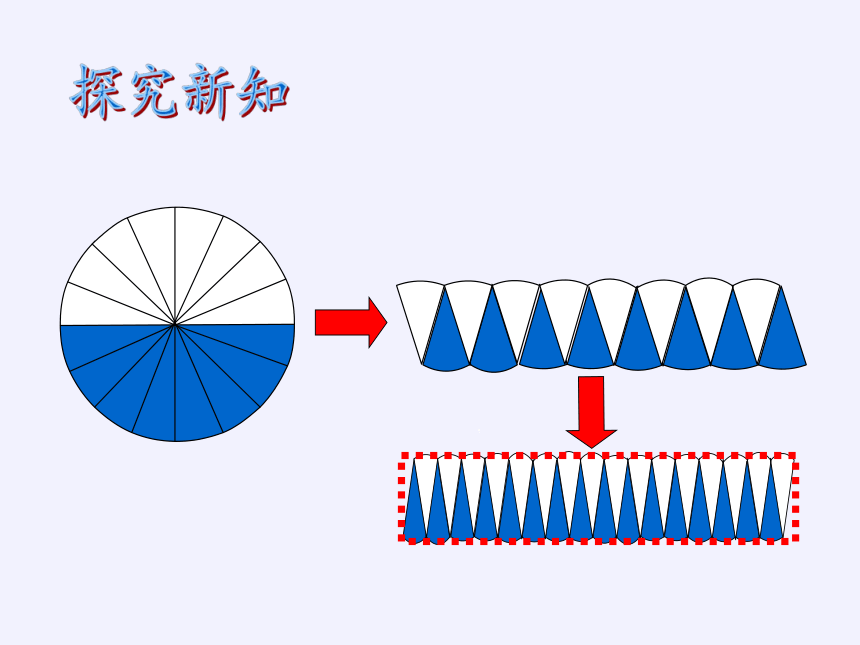
学习圆面积的计算公式时,是把一个圆分割成若干等份,然后拼在一起,结果拼成了一个长方形,从而得出圆的面积公式:S=πr2
探究新知
对于计算圆柱的体积,我们能不能采取同样的方法呢?
小组讨论:
1、圆柱体通过切割、拼凑后,转化为近似什么的图形?什么变了?什么没变?
2、这个转化后的立体图形的底面积与原来的圆柱体的哪一部分有关系?
3、这个近似的立体图形的高与原来圆柱体的哪一部分有关系?
4、圆柱的体积计算公式是什么?用字母如何表示?
探究新知
探究新知
探究新知
探究新知
探究新知
探究新知
1、圆柱体通过切割、拼凑后,转化为近似什么的图形?什么变了?什么没变?
长方体
.
形状
.
体积
.
2、这个转化后的立体图形的底面积与原来的圆柱体的哪一部分有关系?
3、这个近似的立体图形的高与原来圆柱体的哪一部分有关系?
底面积
高
.
.
长方体的底面积
长方体的高
圆柱的底面积
圆柱的高
长方体的体积
圆柱的体积
=
=
×
×
V
=
S
×
h
4、圆柱的体积计算公式是什么?用字母如何表示?
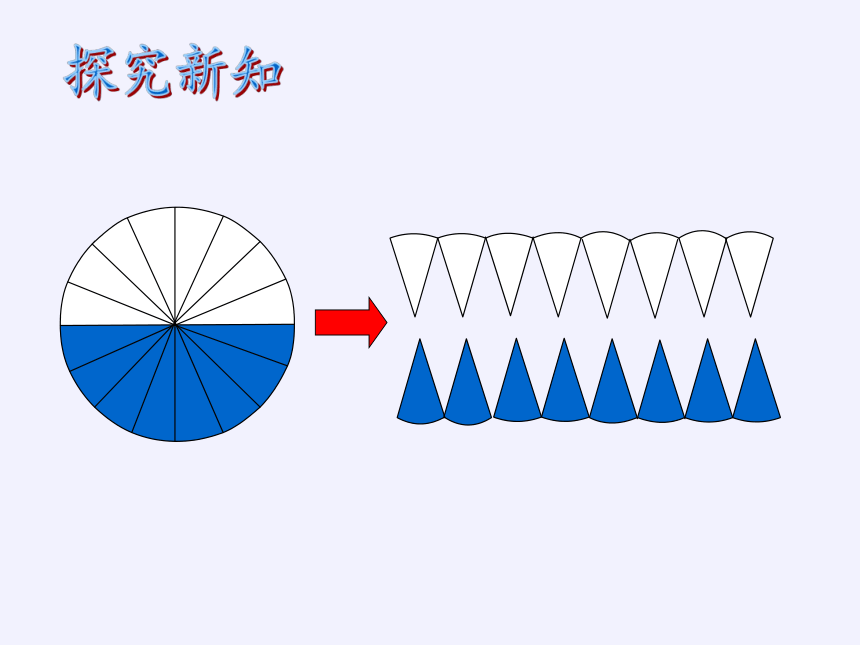
把圆柱的底面平均分的份数越多,切拼成的立体图形越接近长方体。
探究新知
把圆柱的底面平均分的份数越多,切拼成的立体图形越接近长方体。
探究新知
探究新知
把圆柱的底面平均分的份数越多,切拼成的立体图形越接近长方体。
V
=s
h
直柱体的体积
=
底面积×高
圆柱的底面积
圆柱的高
圆柱的体积
=
×
V
=
S
×
h
×
h
=
新知应用
应用一:已知圆柱的底面积和高,求圆柱的体积。
1、一根圆柱形钢材,底面积是40cm2,高是90cm,它的体积是多少?
40×90=3600(cm3)
答:它的体积是3600cm3。
新知应用
应用二:已知圆柱的底面半径和高,求圆柱的体积。
2、一个圆柱形罐头盒的底面半径是5cm,高是
18cm.它的体积是多少?
罐头盒的底面积:
答:它的体积是1413cm3。
罐头盒的体积:
3.14×52=78.5(cm2)
78.5×18=1413(cm3)
综合算式:
3.14×52×18
=3.14×25×18
=1413(cm3)
新知应用
应用三:已知圆柱的底面直径和高,求圆柱的体积.
3、学校要两个同样大小的圆柱形花坛,花坛的底面内直径是3m,高为0.8m,如果里面填土的高度为0.5m,两个花坛中共需要填土多少方?
花坛的底面积:
答:两个花坛中共需要填土7.065方。
两个花坛的体积:
3.14×(3÷2)2
=7.065(cm2)
7.065×0.5×2=7.065(cm3)
综合算式
3.14×(3÷2)2×0.5×2
=7.065(m2)
新知应用
应用四:已知圆柱的底面周长和高,求圆柱的体积。
4、把一个圆柱的侧面展开后得到一个正方形。已知圆柱的高是12.56dm,求圆柱的体积是多少?
圆柱的底面积:
答:它的体积是157.7536cm3。
圆柱的体积:
3.14×22=12.56(cm2)
12.56×12.56=157.7536(cm3)
综合算式
3.14×(12.56÷3.14÷2)2×12.56
=3.14×22×12.56
=157.7536(cm3)
圆柱的半径:
r=c÷π÷?2=
12.56÷3.14÷?2=2(cm)
本节课,你有哪些收获???
1、圆柱体的体积公式的探索:将圆柱体通过分割、拼接的方式,转成近似长方体的立体图形。根据长方体的体积公式,推导出圆柱体的体积公式。
2、圆柱体的体积=底面积×高
V=Sh
=
知道S和h:
知道r和h:
知道d和h:
知道C和h:
V=Sh
V=πr2×h
V=π(C÷π÷2)2×h
V=π(d÷2)2×h
怎样求出饮料罐的体积?
谢
谢
圆柱的体积
长
高
宽
棱
长
长
v
=a
b
h
v
3
正
=a
V=S
h
底
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
复
习:
真
棒!
S
S
探究新知
能不能猜想一下圆柱的体积可能与什么有关?到底要怎么研究呢?
你会计算圆柱的体积吗?
探究新知
探究新知
探究新知
我们知道
:
学习圆面积的计算公式时,是把一个圆分割成若干等份,然后拼在一起,结果拼成了一个长方形,从而得出圆的面积公式:S=πr2
探究新知
对于计算圆柱的体积,我们能不能采取同样的方法呢?
小组讨论:
1、圆柱体通过切割、拼凑后,转化为近似什么的图形?什么变了?什么没变?
2、这个转化后的立体图形的底面积与原来的圆柱体的哪一部分有关系?
3、这个近似的立体图形的高与原来圆柱体的哪一部分有关系?
4、圆柱的体积计算公式是什么?用字母如何表示?
探究新知
探究新知
探究新知
探究新知
探究新知
探究新知
1、圆柱体通过切割、拼凑后,转化为近似什么的图形?什么变了?什么没变?
长方体
.
形状
.
体积
.
2、这个转化后的立体图形的底面积与原来的圆柱体的哪一部分有关系?
3、这个近似的立体图形的高与原来圆柱体的哪一部分有关系?
底面积
高
.
.
长方体的底面积
长方体的高
圆柱的底面积
圆柱的高
长方体的体积
圆柱的体积
=
=
×
×
V
=
S
×
h
4、圆柱的体积计算公式是什么?用字母如何表示?
把圆柱的底面平均分的份数越多,切拼成的立体图形越接近长方体。
探究新知
把圆柱的底面平均分的份数越多,切拼成的立体图形越接近长方体。
探究新知
探究新知
把圆柱的底面平均分的份数越多,切拼成的立体图形越接近长方体。
V
=s
h
直柱体的体积
=
底面积×高
圆柱的底面积
圆柱的高
圆柱的体积
=
×
V
=
S
×
h
×
h
=
新知应用
应用一:已知圆柱的底面积和高,求圆柱的体积。
1、一根圆柱形钢材,底面积是40cm2,高是90cm,它的体积是多少?
40×90=3600(cm3)
答:它的体积是3600cm3。
新知应用
应用二:已知圆柱的底面半径和高,求圆柱的体积。
2、一个圆柱形罐头盒的底面半径是5cm,高是
18cm.它的体积是多少?
罐头盒的底面积:
答:它的体积是1413cm3。
罐头盒的体积:
3.14×52=78.5(cm2)
78.5×18=1413(cm3)
综合算式:
3.14×52×18
=3.14×25×18
=1413(cm3)
新知应用
应用三:已知圆柱的底面直径和高,求圆柱的体积.
3、学校要两个同样大小的圆柱形花坛,花坛的底面内直径是3m,高为0.8m,如果里面填土的高度为0.5m,两个花坛中共需要填土多少方?
花坛的底面积:
答:两个花坛中共需要填土7.065方。
两个花坛的体积:
3.14×(3÷2)2
=7.065(cm2)
7.065×0.5×2=7.065(cm3)
综合算式
3.14×(3÷2)2×0.5×2
=7.065(m2)
新知应用
应用四:已知圆柱的底面周长和高,求圆柱的体积。
4、把一个圆柱的侧面展开后得到一个正方形。已知圆柱的高是12.56dm,求圆柱的体积是多少?
圆柱的底面积:
答:它的体积是157.7536cm3。
圆柱的体积:
3.14×22=12.56(cm2)
12.56×12.56=157.7536(cm3)
综合算式
3.14×(12.56÷3.14÷2)2×12.56
=3.14×22×12.56
=157.7536(cm3)
圆柱的半径:
r=c÷π÷?2=
12.56÷3.14÷?2=2(cm)
本节课,你有哪些收获???
1、圆柱体的体积公式的探索:将圆柱体通过分割、拼接的方式,转成近似长方体的立体图形。根据长方体的体积公式,推导出圆柱体的体积公式。
2、圆柱体的体积=底面积×高
V=Sh
=
知道S和h:
知道r和h:
知道d和h:
知道C和h:
V=Sh
V=πr2×h
V=π(C÷π÷2)2×h
V=π(d÷2)2×h
怎样求出饮料罐的体积?
谢
谢
