六年级数学下册课件-4.1.2 比例的基本性质-人教版(共31张PPT)
文档属性
| 名称 | 六年级数学下册课件-4.1.2 比例的基本性质-人教版(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 657.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览










文档简介
(共31张PPT)
比例的基本性质
巩固新知:
应用比例的意义判断下面两个比是否能组成比例:
①6∶9
和
9∶12
②6∶10
和
9∶15
③∶和
6∶4
④0.6∶0.2和
∶
巩固新知:
应用比例的意义判断下面两个比是否能组成比例:
①6∶9
和
9∶12
所以:
6∶9
和
9∶12
不能组成比例
因为:
6
∶
9
=
9∶12
=
≠
②6∶10
和
9∶15
所以:
6∶10
和
9∶15
能组成比例.
因为:
6
∶
10
=
9∶15
=
=
∶
和
6∶4
所以:
∶
和
6∶4
能组成比例.
因为:
∶
=
6∶4
=
=
④0.6∶0.2和
∶
所以:
0.6∶0.2
和
∶
能组成比例.
因为:0.6
∶
0.2
=
3
∶
=
3
3
=
3
1.6
60
40
2.4
︰
︰
=
内项
外项
=
外项
内项
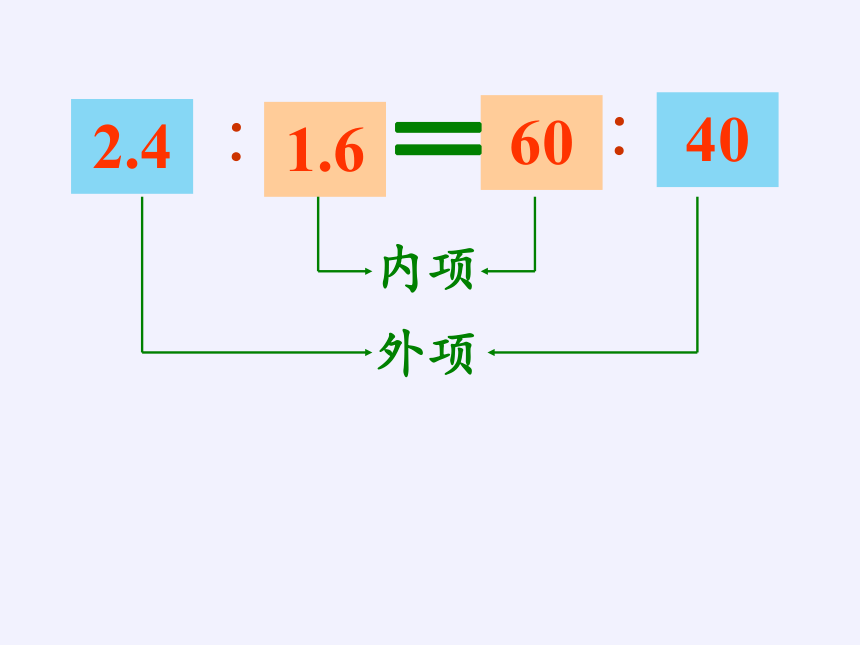
2.4∶1.6=
60
∶40
外项
内项
=
内项
外项
比较下面两种形式的比例,你有什么发现呢?
指出下面比例的外项和内项.
4.5∶2.7
=
10
∶6
6
∶10
=
9
∶15
∶
=
6
∶4
0.6
∶0.2
∶
=
外项
外项
内项
内项
外项
内项
外项
内项
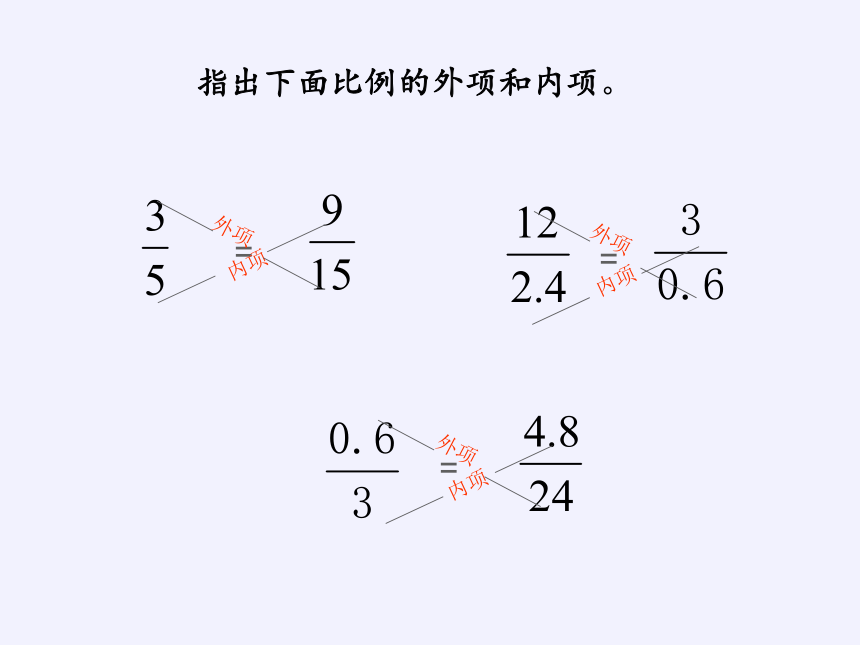
指出下面比例的外项和内项。
=
内项
外项
=
内项
外项
=
内项
外项
2.4:1.6=60:40
=
计算下面比例中两个外项的积和两个内项的积。比较一下,你能发现什么?和组内成员交流你的想法。
外项积:2.4×40=96
内项积:1.6×60=96
外项积:3×15=45
内项积:5×9=45
4.5∶2.7
=
10
∶6
6:10
=
9
∶15
选择一组你喜欢的比例,计算两个外项的积和两个内项的积,验证你刚才的发现。
=
=
4.5∶2.7
=
10
∶6
外项积:4.5×6=27
内项积:2.7×10=27
6
∶10
=
9
∶15
外项积:6×15
=
90
内项积:10×9
=
90
=
外项积:0.6×24=14.4
内项积:3×4.8=14.4
=
外项积:12×0.6=7.2
内项积:2.4×3=7.2
︰
︰
=
外项
内项
内项积是:
1.6
×
60
=96
外项积是:
2.4
×
40
=
96
2.4
40
×
×
=
1.6
60
1.6
60
40
2.4
︰
︰
=
外项
内项
=
2.4×40
1.6×60
在比例里,两个外项的积等于两个内项的积。
2.4︰1.6
60︰40
=
2.4
1.6
=
60
40
外项
外项
内项
内项
交叉相乘
=
2.4×40
1.6×60
你能用字母表示这个性质吗?
用字母表示比例的基本性质:a:b=c:d(b、d≠0)
=
或
ad=bc
填空
⒈组成比例的四个数,叫做比例的(
),两端的两项叫做比例的(
),中间的两项叫做比例的(
)。
项
外项
内项
⒉在比例中,两个(
)的积等于两个(
)的积。
外项
内项
⒊2、3、6、9可以组成比例,如果确定2是比例的第一项,9为比例的第四项,那么这个比例是
(
)
2﹕3=6﹕9
或2﹕6=3﹕9
试一试
应用比例的基本性质,判断下面哪组中的两个比可以组成比例。
6:3和8:5
0.2:2.5和4:50
∶和∶
1.2∶和∶5
试一试
应用比例的基本性质,判断下面哪组中的两个比可以组成比例。
6:3和8:5
6×5=30
3×8=24
不能组成比例
≠
30
24
0.2:2.5和4:50
0.2×50=10
2.5×4=10
10
=
10
可以组成比例
0.2:2.5=4:50
∶和∶
×=
×=
=
可以组成比例
应用比例的基本性质,判断下面哪组中的两个比可以组成比例。
1.2∶和∶5
1.2×5=6
×=0.6
6
≠
0.6
不能组成比例
∶=∶
(√)
(×)
(×)
(1)在比例中,两个外项的积减去两
个内项的积,差是0.
(2)18:30和3:5可以组成比例。
(3)如果4:Ⅹ=3:Y,(X和Y均不为0),
那么4X=3Y.
(4)因为3:6=5:10,所以3×5=10×6
判断
(√)
(
解决问题
1.
李叔叔承包了两块水稻田,面积分别是0.5公顷和0.8公顷。秋收时,
两块水稻田的产量分别为3.75吨和6吨。
(1)两块水稻田的产量与面积之比,是否可以组成比例?
0.5:0.8=3.75:6
?
0.5×6=3
0.8×3.75=3
答:两块水稻田的产量与面积之比,可以组成比例。
(
解决问题
(2)如果可以组成比例,指出比例的内项和外项。
0.5:0.8=3.75:
6
答:比例的内项是0.8和3.75,比例的外项是0.5和6。
内项
外项
1.
李叔叔承包了两块水稻田,面积分别是0.5公顷和0.8公顷。秋收时,
两块水稻田的产量分别为3.75吨和6吨。
谈收获:
说说这节课你有哪些收获?
布置作业
作业:第43页练习八,第5题、
第6题、第7题。
谢
谢
比例的基本性质
巩固新知:
应用比例的意义判断下面两个比是否能组成比例:
①6∶9
和
9∶12
②6∶10
和
9∶15
③∶和
6∶4
④0.6∶0.2和
∶
巩固新知:
应用比例的意义判断下面两个比是否能组成比例:
①6∶9
和
9∶12
所以:
6∶9
和
9∶12
不能组成比例
因为:
6
∶
9
=
9∶12
=
≠
②6∶10
和
9∶15
所以:
6∶10
和
9∶15
能组成比例.
因为:
6
∶
10
=
9∶15
=
=
∶
和
6∶4
所以:
∶
和
6∶4
能组成比例.
因为:
∶
=
6∶4
=
=
④0.6∶0.2和
∶
所以:
0.6∶0.2
和
∶
能组成比例.
因为:0.6
∶
0.2
=
3
∶
=
3
3
=
3
1.6
60
40
2.4
︰
︰
=
内项
外项
=
外项
内项
2.4∶1.6=
60
∶40
外项
内项
=
内项
外项
比较下面两种形式的比例,你有什么发现呢?
指出下面比例的外项和内项.
4.5∶2.7
=
10
∶6
6
∶10
=
9
∶15
∶
=
6
∶4
0.6
∶0.2
∶
=
外项
外项
内项
内项
外项
内项
外项
内项
指出下面比例的外项和内项。
=
内项
外项
=
内项
外项
=
内项
外项
2.4:1.6=60:40
=
计算下面比例中两个外项的积和两个内项的积。比较一下,你能发现什么?和组内成员交流你的想法。
外项积:2.4×40=96
内项积:1.6×60=96
外项积:3×15=45
内项积:5×9=45
4.5∶2.7
=
10
∶6
6:10
=
9
∶15
选择一组你喜欢的比例,计算两个外项的积和两个内项的积,验证你刚才的发现。
=
=
4.5∶2.7
=
10
∶6
外项积:4.5×6=27
内项积:2.7×10=27
6
∶10
=
9
∶15
外项积:6×15
=
90
内项积:10×9
=
90
=
外项积:0.6×24=14.4
内项积:3×4.8=14.4
=
外项积:12×0.6=7.2
内项积:2.4×3=7.2
︰
︰
=
外项
内项
内项积是:
1.6
×
60
=96
外项积是:
2.4
×
40
=
96
2.4
40
×
×
=
1.6
60
1.6
60
40
2.4
︰
︰
=
外项
内项
=
2.4×40
1.6×60
在比例里,两个外项的积等于两个内项的积。
2.4︰1.6
60︰40
=
2.4
1.6
=
60
40
外项
外项
内项
内项
交叉相乘
=
2.4×40
1.6×60
你能用字母表示这个性质吗?
用字母表示比例的基本性质:a:b=c:d(b、d≠0)
=
或
ad=bc
填空
⒈组成比例的四个数,叫做比例的(
),两端的两项叫做比例的(
),中间的两项叫做比例的(
)。
项
外项
内项
⒉在比例中,两个(
)的积等于两个(
)的积。
外项
内项
⒊2、3、6、9可以组成比例,如果确定2是比例的第一项,9为比例的第四项,那么这个比例是
(
)
2﹕3=6﹕9
或2﹕6=3﹕9
试一试
应用比例的基本性质,判断下面哪组中的两个比可以组成比例。
6:3和8:5
0.2:2.5和4:50
∶和∶
1.2∶和∶5
试一试
应用比例的基本性质,判断下面哪组中的两个比可以组成比例。
6:3和8:5
6×5=30
3×8=24
不能组成比例
≠
30
24
0.2:2.5和4:50
0.2×50=10
2.5×4=10
10
=
10
可以组成比例
0.2:2.5=4:50
∶和∶
×=
×=
=
可以组成比例
应用比例的基本性质,判断下面哪组中的两个比可以组成比例。
1.2∶和∶5
1.2×5=6
×=0.6
6
≠
0.6
不能组成比例
∶=∶
(√)
(×)
(×)
(1)在比例中,两个外项的积减去两
个内项的积,差是0.
(2)18:30和3:5可以组成比例。
(3)如果4:Ⅹ=3:Y,(X和Y均不为0),
那么4X=3Y.
(4)因为3:6=5:10,所以3×5=10×6
判断
(√)
(
解决问题
1.
李叔叔承包了两块水稻田,面积分别是0.5公顷和0.8公顷。秋收时,
两块水稻田的产量分别为3.75吨和6吨。
(1)两块水稻田的产量与面积之比,是否可以组成比例?
0.5:0.8=3.75:6
?
0.5×6=3
0.8×3.75=3
答:两块水稻田的产量与面积之比,可以组成比例。
(
解决问题
(2)如果可以组成比例,指出比例的内项和外项。
0.5:0.8=3.75:
6
答:比例的内项是0.8和3.75,比例的外项是0.5和6。
内项
外项
1.
李叔叔承包了两块水稻田,面积分别是0.5公顷和0.8公顷。秋收时,
两块水稻田的产量分别为3.75吨和6吨。
谈收获:
说说这节课你有哪些收获?
布置作业
作业:第43页练习八,第5题、
第6题、第7题。
谢
谢
