六年级数学下册课件-4.2.1 正比例10-人教版(共23张PPT)
文档属性
| 名称 | 六年级数学下册课件-4.2.1 正比例10-人教版(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 236.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
正比例
星期天,小明和爸爸做着车,去接在出版社工作的妈妈,他们做的车2小时行驶了180千米。
汽车平均每小时行驶多少千米?
180÷2=90(千米)
路程÷时间=速度
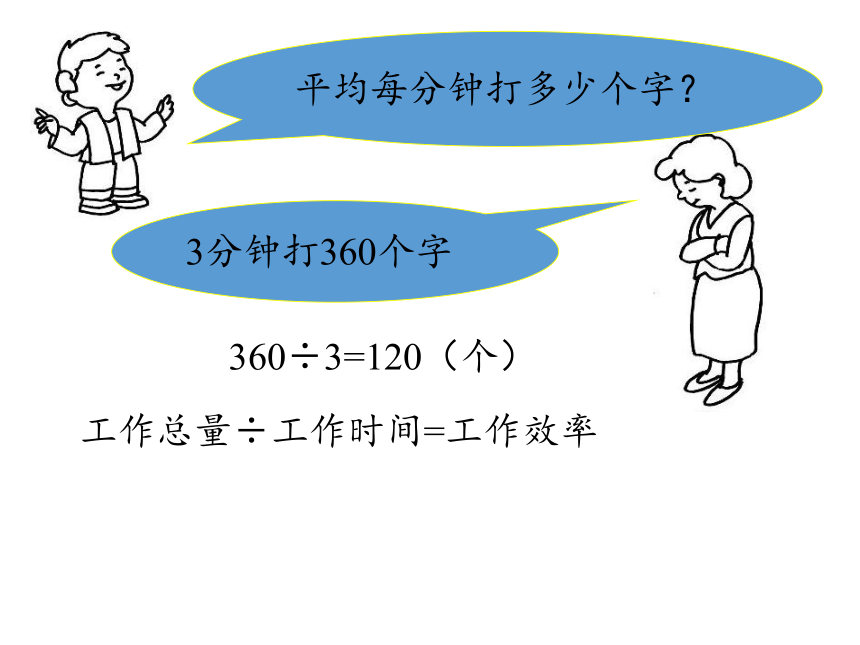
360÷3=120(个)
工作总量÷工作时间=工作效率
平均每分钟打多少个字?
3分钟打360个字
小明花了10元钱买了2支同样的钢笔,每支钢笔多少钱?
10÷2=5(元)
总价÷数量=单价
路程÷时间=速度
工作总量÷工作时间=工作效率
总价÷数量=单价
汽车行驶的时间和路程如下表。
2
观察上表,回答下面的问题:
时间/时
1
2
3
4
5
6
7
8
路程/千米
90
180
270
360
450
540
630
720
(1)表中有哪两种量?
答:表中有汽车行驶的路程和时间两种量。
2
观察上表,回答下面的问题:
时间/时
1
2
3
4
5
6
7
8
路程/千米
90
180
270
360
450
540
630
720
(2)路程是怎样随时间的变化而变化的?
答:时间增加,所行的路程也相应增
加;时间减少,所行的路程也相应减少。
汽车行驶的时间和路程如下表。
观察上表,回答下面的问题:
90
1
=
90
180
2
=
90
270
3
=
90
时间/时
1
2
3
4
5
6
7
8
路程/千米
90
180
270
360
450
540
630
720
(3)相对应的路程与时间的比值各是多少?
汽车行驶的时间和路程如下表。
时间/时
1
2
3
4
5
6
7
8
路程/千米
90
180
270
360
450
540
630
720
(4)从表中你发现了什么规律?
路程
时间
=
速度(一定)
汽车行驶的时间和路程如下表。
路程
时间
=
速度(一定)
2
工作总量和工作时间如下表:
时间/分
1
2
3
4
5
字数/个
120
240
360
480
600
(1)表中有哪两种量?它们是不是相关联的量?
(2)它们的变化规律是怎样的?
(3)写出两种量中相对应的两个数的比值,并比较它们的大小。
(4)这个比值表示什么?
工作总量
工作时间
=
工作效率(一定)
(1)表中有哪两种量?
(2)数量和总价的变化有什么规律?
(3)你能说出这两个量之间的比吗?比值是多少?比值表示什么?
(4)它们之间的关系式是?
4
3
2
数量/支
45
40
35
30
25
20
15
10
总价/元
5
8
7
6
9
钢笔的总价和数量如下表:
那么要判断两种量是否成正比例该看什么?
1.都是两种相关联的量,一种量变化,另一种量也相应变化。
2.它们的比值(商)一定(即不变)。
1、一辆汽车匀速行驶,每小时行60千米.
(路程)和(时间)是两种相关联的量,(路程)随着(时间)的变化而变化。
这两种量相对应的两个数的(比值)一定,所以这两种量叫做成(正比例)的量,它们的关系叫做(
正比例
)关系.
…
420
360
300
240
180
120
60
路程(千米)
…
7
6
5
4
3
2
1
时间(时)
2、在一间布店的柜台上,有一张写着某种花布的米数和总价如下表:
(1
)表中有_____和______两种量。
(2)比值实际上表示_______,请用式子表示它们
的关系,关系式为:
(3)下结论:花布的_______一定,______和________成正比例。
数量x(米)
1
2
3
4
5
6
…
…
总价y(元)
9.5
19
28.5
38
47.5
57
…
…
数量
总价
单价
单价
总价
数量
3.已知a和b成正比例,完成下表。
a
30
50
65
1.5
b
6
3
8
0.5
15
0.3
13
40
2.5
10
拓展创新
4.审判官:判断下面每题中的两种量是不是成正比例,并说明理由。
(1)大豆的出油率一定,豆油的质量和大豆的质量。
(
)
√
因为:
豆油的质量
大豆的质量
=出油率(一定)
所以:豆油的质量和大豆的质量成正比例。
(2)一个人的身高和体重。(
)
理由:虽然人的身高增加,体重也相应增加,但是体重与身高的比值不一定,所以,人的身高和体重不成正比例。
×
√
(3)圆的直径和周长。(
)
因为:
圆的周长
圆的直径
=
圆周率(一定)
所以:圆的直径和周长成正比例
(4)差一定,被减数和减数。(
)
×
因为:被减数
–
减数
=
差
所以:被减数与减数不成比例。
(5)火车的速度一定,路程和时间。(
)
√
5、如果x和y是两种相关联的量,并且
y=3x,那么y
和x成_______
成正比例
经过今天的学习,
你有哪些收获?
谢
谢
正比例
星期天,小明和爸爸做着车,去接在出版社工作的妈妈,他们做的车2小时行驶了180千米。
汽车平均每小时行驶多少千米?
180÷2=90(千米)
路程÷时间=速度
360÷3=120(个)
工作总量÷工作时间=工作效率
平均每分钟打多少个字?
3分钟打360个字
小明花了10元钱买了2支同样的钢笔,每支钢笔多少钱?
10÷2=5(元)
总价÷数量=单价
路程÷时间=速度
工作总量÷工作时间=工作效率
总价÷数量=单价
汽车行驶的时间和路程如下表。
2
观察上表,回答下面的问题:
时间/时
1
2
3
4
5
6
7
8
路程/千米
90
180
270
360
450
540
630
720
(1)表中有哪两种量?
答:表中有汽车行驶的路程和时间两种量。
2
观察上表,回答下面的问题:
时间/时
1
2
3
4
5
6
7
8
路程/千米
90
180
270
360
450
540
630
720
(2)路程是怎样随时间的变化而变化的?
答:时间增加,所行的路程也相应增
加;时间减少,所行的路程也相应减少。
汽车行驶的时间和路程如下表。
观察上表,回答下面的问题:
90
1
=
90
180
2
=
90
270
3
=
90
时间/时
1
2
3
4
5
6
7
8
路程/千米
90
180
270
360
450
540
630
720
(3)相对应的路程与时间的比值各是多少?
汽车行驶的时间和路程如下表。
时间/时
1
2
3
4
5
6
7
8
路程/千米
90
180
270
360
450
540
630
720
(4)从表中你发现了什么规律?
路程
时间
=
速度(一定)
汽车行驶的时间和路程如下表。
路程
时间
=
速度(一定)
2
工作总量和工作时间如下表:
时间/分
1
2
3
4
5
字数/个
120
240
360
480
600
(1)表中有哪两种量?它们是不是相关联的量?
(2)它们的变化规律是怎样的?
(3)写出两种量中相对应的两个数的比值,并比较它们的大小。
(4)这个比值表示什么?
工作总量
工作时间
=
工作效率(一定)
(1)表中有哪两种量?
(2)数量和总价的变化有什么规律?
(3)你能说出这两个量之间的比吗?比值是多少?比值表示什么?
(4)它们之间的关系式是?
4
3
2
数量/支
45
40
35
30
25
20
15
10
总价/元
5
8
7
6
9
钢笔的总价和数量如下表:
那么要判断两种量是否成正比例该看什么?
1.都是两种相关联的量,一种量变化,另一种量也相应变化。
2.它们的比值(商)一定(即不变)。
1、一辆汽车匀速行驶,每小时行60千米.
(路程)和(时间)是两种相关联的量,(路程)随着(时间)的变化而变化。
这两种量相对应的两个数的(比值)一定,所以这两种量叫做成(正比例)的量,它们的关系叫做(
正比例
)关系.
…
420
360
300
240
180
120
60
路程(千米)
…
7
6
5
4
3
2
1
时间(时)
2、在一间布店的柜台上,有一张写着某种花布的米数和总价如下表:
(1
)表中有_____和______两种量。
(2)比值实际上表示_______,请用式子表示它们
的关系,关系式为:
(3)下结论:花布的_______一定,______和________成正比例。
数量x(米)
1
2
3
4
5
6
…
…
总价y(元)
9.5
19
28.5
38
47.5
57
…
…
数量
总价
单价
单价
总价
数量
3.已知a和b成正比例,完成下表。
a
30
50
65
1.5
b
6
3
8
0.5
15
0.3
13
40
2.5
10
拓展创新
4.审判官:判断下面每题中的两种量是不是成正比例,并说明理由。
(1)大豆的出油率一定,豆油的质量和大豆的质量。
(
)
√
因为:
豆油的质量
大豆的质量
=出油率(一定)
所以:豆油的质量和大豆的质量成正比例。
(2)一个人的身高和体重。(
)
理由:虽然人的身高增加,体重也相应增加,但是体重与身高的比值不一定,所以,人的身高和体重不成正比例。
×
√
(3)圆的直径和周长。(
)
因为:
圆的周长
圆的直径
=
圆周率(一定)
所以:圆的直径和周长成正比例
(4)差一定,被减数和减数。(
)
×
因为:被减数
–
减数
=
差
所以:被减数与减数不成比例。
(5)火车的速度一定,路程和时间。(
)
√
5、如果x和y是两种相关联的量,并且
y=3x,那么y
和x成_______
成正比例
经过今天的学习,
你有哪些收获?
谢
谢
