2020-2021学年苏科版八年级上册数学5.2平面直角坐标系(3) 巩固训练卷(Word版,有答案)
文档属性
| 名称 | 2020-2021学年苏科版八年级上册数学5.2平面直角坐标系(3) 巩固训练卷(Word版,有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 249.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 14:16:11 | ||
图片预览

文档简介
2020-2021学年苏科版八年级上学期数学5.2平面直角坐标系(3)
巩固训练卷
一、选择题
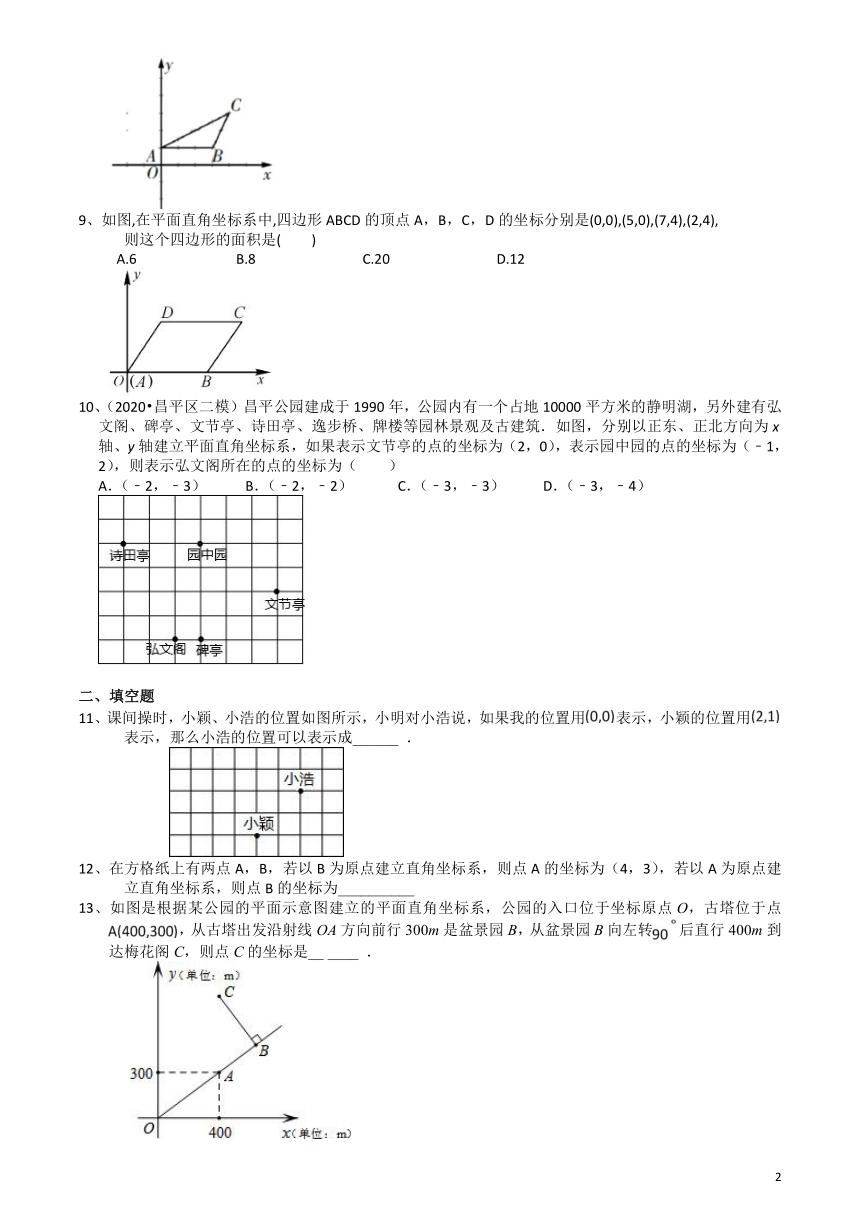
1、在如图所示的象棋盘上,若“帅”和“相”所在的坐标分别是和上,则“炮”的坐标是
B.
C.
D.
2、如图,在的正方形网格中由四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是
A点
B.
B点
C.
C点
D.
D点
3、长方形ABCD的长为6,宽为4,建立平面直角坐标系如图所示,则下列各点中,不在这个长方形上的是(
)
A.
(3,2)
B.
(-2,-3)
C.
(0,2)
D.
(-3,2)
4、如图,在平面直角坐标系中,正方形OACB的顶点O,C的坐标分别是(0,0),(2,0),
则顶点B的坐标是(
)
A.(1,1)
B.(-1,-1)
C.(1,-1)
D.(-1,1)
5、设三角形三个顶点坐标分别为A(0,0),B(3,0),C(3,-3),则这个三角形是(
)
A.等边三角形
B.等腰直角三角形
C.钝角三角形
D.锐角三角形
6、如图,AB∥CD,AD∥BC∥x轴,下列说法正确的是(
)
A.A与D的横坐标相同
B.A与B的横坐标相同
C.B与C的纵坐标相同
D.C与D的纵坐标相同
7、等腰三角形ABC在直角坐标系中,底边的两端点坐标是(-2,0),(6,0),
则其顶点的坐标,能确定的是(
)
A.横坐标
B.纵坐标
C.横坐标及纵坐标
D.横坐标或纵坐标
8、如图,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),如果△ABD与△ABC全等,
那么点D的坐标是_________.
9、如图,在平面直角坐标系中,四边形ABCD的顶点A,B,C,D的坐标分别是(0,0),(5,0),(7,4),(2,4),
则这个四边形的面积是(
)
A.6
B.8
C.20
D.12
10、(2020?昌平区二模)昌平公园建成于1990年,公园内有一个占地10000平方米的静明湖,另外建有弘文阁、碑亭、文节亭、诗田亭、逸步桥、牌楼等园林景观及古建筑.如图,分别以正东、正北方向为x轴、y轴建立平面直角坐标系,如果表示文节亭的点的坐标为(2,0),表示园中园的点的坐标为(﹣1,2),则表示弘文阁所在的点的坐标为( )
A.(﹣2,﹣3)
B.(﹣2,﹣2)
C.(﹣3,﹣3)
D.(﹣3,﹣4)
二、填空题
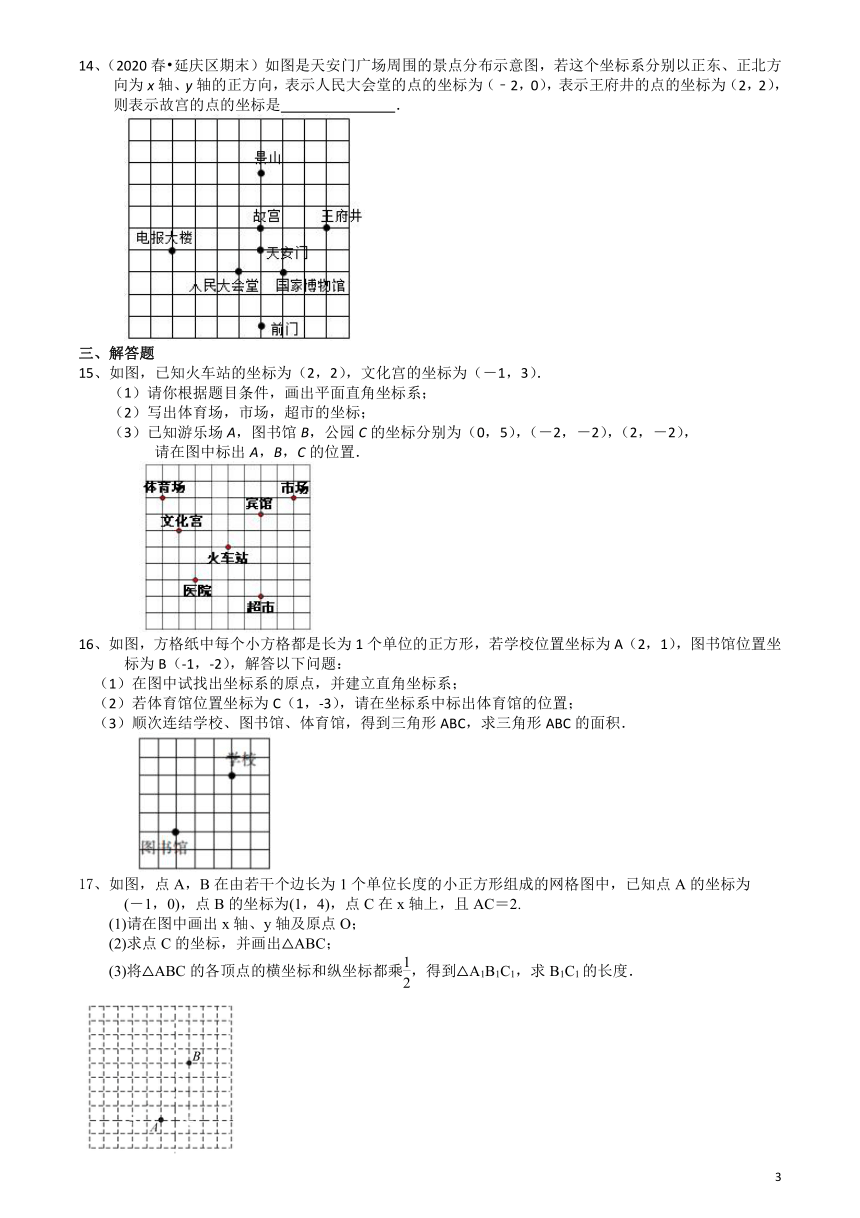
11、课间操时,小颖、小浩的位置如图所示,小明对小浩说,如果我的位置用表示,小颖的位置用表示,那么小浩的位置可以表示成______
.
12、在方格纸上有两点A,B,若以B为原点建立直角坐标系,则点A的坐标为(4,3),若以A为原点建立直角坐标系,则点B的坐标为__________
13、如图是根据某公园的平面示意图建立的平面直角坐标系,公园的入口位于坐标原点O,古塔位于点,从古塔出发沿射线OA方向前行300m是盆景园B,从盆景园B向左转后直行400m到达梅花阁C,则点C的坐标是__?____
.
14、(2020春?延庆区期末)如图是天安门广场周围的景点分布示意图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示人民大会堂的点的坐标为(﹣2,0),表示王府井的点的坐标为(2,2),则表示故宫的点的坐标是
.
三、解答题
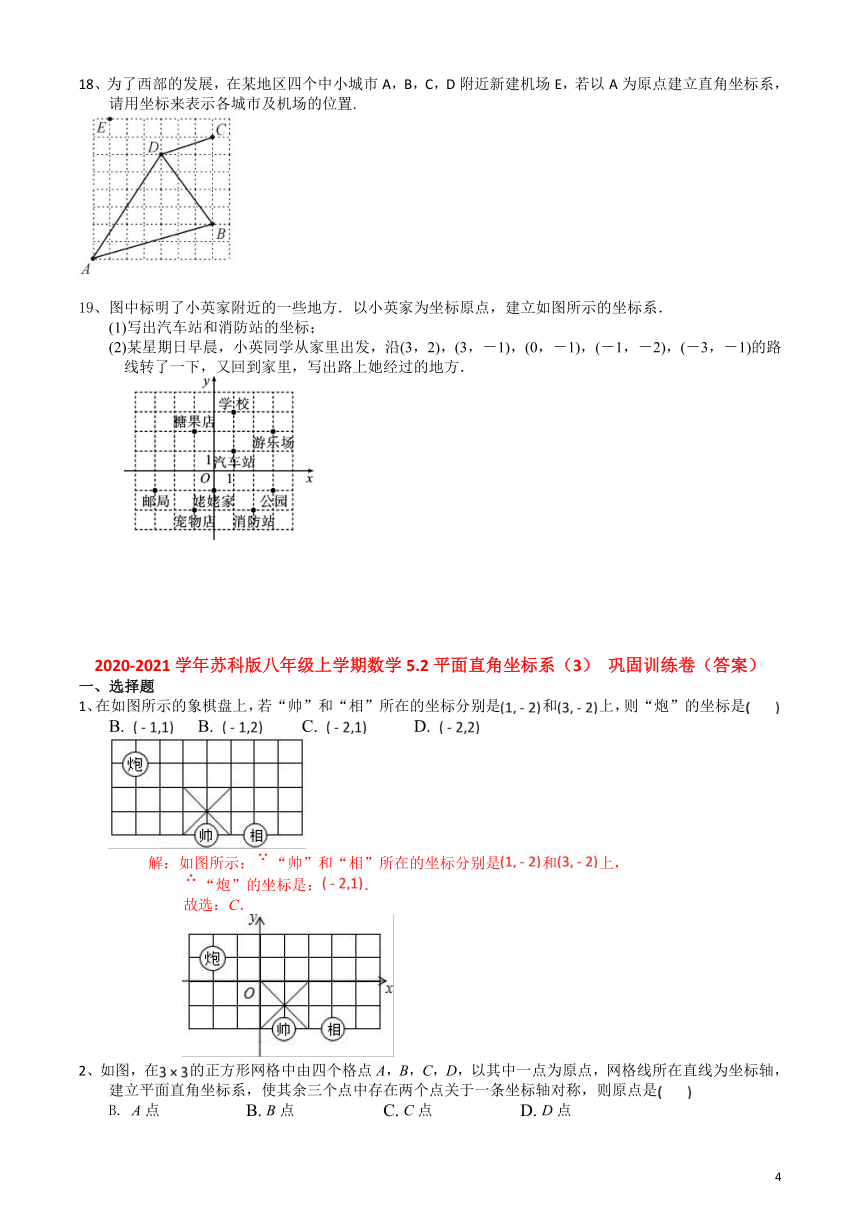
15、如图,已知火车站的坐标为(2,2),文化宫的坐标为(-1,3).
(1)请你根据题目条件,画出平面直角坐标系;
(2)写出体育场,市场,超市的坐标;
(3)已知游乐场A,图书馆B,公园C的坐标分别为(0,5),(-2,-2),(2,-2),
请在图中标出A,B,C的位置.
16、如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(2,1),图书馆位置坐标为B(-1,-2),解答以下问题:
(1)在图中试找出坐标系的原点,并建立直角坐标系;
(2)若体育馆位置坐标为C(1,-3),请在坐标系中标出体育馆的位置;
(3)顺次连结学校、图书馆、体育馆,得到三角形ABC,求三角形ABC的面积.
17、如图,点A,B在由若干个边长为1个单位长度的小正方形组成的网格图中,已知点A的坐标为
(-1,0),点B的坐标为(1,4),点C在x轴上,且AC=2.
(1)请在图中画出x轴、y轴及原点O;
(2)求点C的坐标,并画出△ABC;
(3)将△ABC的各顶点的横坐标和纵坐标都乘,得到△A1B1C1,求B1C1的长度.
18、为了西部的发展,在某地区四个中小城市A,B,C,D附近新建机场E,若以A为原点建立直角坐标系,请用坐标来表示各城市及机场的位置.
19、图中标明了小英家附近的一些地方.以小英家为坐标原点,建立如图所示的坐标系.
(1)写出汽车站和消防站的坐标;
(2)某星期日早晨,小英同学从家里出发,沿(3,2),(3,-1),(0,-1),(-1,-2),(-3,-1)的路线转了一下,又回到家里,写出路上她经过的地方.
2020-2021学年苏科版八年级上学期数学5.2平面直角坐标系(3)
巩固训练卷(答案)
一、选择题
1、在如图所示的象棋盘上,若“帅”和“相”所在的坐标分别是和上,则“炮”的坐标是
B.
C.
D.
解:如图所示:“帅”和“相”所在的坐标分别是和上,
“炮”的坐标是:.
故选:C.
2、如图,在的正方形网格中由四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是
A点
B.
B点
C.
C点
D.
D点
解:当以点B为原点时,,,
则点A和点C关于y轴对称,
符合条件,
故选:B
3、长方形ABCD的长为6,宽为4,建立平面直角坐标系如图所示,则下列各点中,不在这个长方形上的是(
B
)
A.
(3,2)
B.
(-2,-3)
C.
(0,2)
D.
(-3,2)
4、如图,在平面直角坐标系中,正方形OACB的顶点O,C的坐标分别是(0,0),(2,0),
则顶点B的坐标是(
C
)
A.(1,1)
B.(-1,-1)
C.(1,-1)
D.(-1,1)
5、设三角形三个顶点坐标分别为A(0,0),B(3,0),C(3,-3),则这个三角形是(
B
)
A.等边三角形
B.等腰直角三角形
C.钝角三角形
D.锐角三角形
6、如图,AB∥CD,AD∥BC∥x轴,下列说法正确的是(
C
)
A.A与D的横坐标相同
B.A与B的横坐标相同
C.B与C的纵坐标相同
D.C与D的纵坐标相同
7、等腰三角形ABC在直角坐标系中,底边的两端点坐标是(-2,0),(6,0),
则其顶点的坐标,能确定的是(
A
)
A.横坐标
B.纵坐标
C.横坐标及纵坐标
D.横坐标或纵坐标
8、如图,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),如果△ABD与△ABC全等,
那么点D的坐标是___(4,-1)或(-1,3)或(-1,-1)______.
9、如图,在平面直角坐标系中,四边形ABCD的顶点A,B,C,D的坐标分别是(0,0),(5,0),(7,4),(2,4),
则这个四边形的面积是(
C
)
A.6
B.8
C.20
D.12
10、(2020?昌平区二模)昌平公园建成于1990年,公园内有一个占地10000平方米的静明湖,另外建有弘文阁、碑亭、文节亭、诗田亭、逸步桥、牌楼等园林景观及古建筑.如图,分别以正东、正北方向为x轴、y轴建立平面直角坐标系,如果表示文节亭的点的坐标为(2,0),表示园中园的点的坐标为(﹣1,2),则表示弘文阁所在的点的坐标为( )
A.(﹣2,﹣3)
B.(﹣2,﹣2)
C.(﹣3,﹣3)
D.(﹣3,﹣4)
【解答】解:如图所示:弘文阁所在的点的坐标为:(﹣2,﹣2).
故选:B.
二、填空题
11、课间操时,小颖、小浩的位置如图所示,小明对小浩说,如果我的位置用表示,小颖的位置用表示,那么小浩的位置可以表示成__??____
.
12、在方格纸上有两点A,B,若以B为原点建立直角坐标系,则点A的坐标为(4,3),若以A为原点建立直角坐标系,则点B的坐标为____(-4,-3)______
13、如图是根据某公园的平面示意图建立的平面直角坐标系,公园的入口位于坐标原点O,古塔位于点,从古塔出发沿射线OA方向前行300m是盆景园B,从盆景园B向左转后直行400m到达梅花阁C,则点C的坐标是__?____
.
14、(2020春?延庆区期末)如图是天安门广场周围的景点分布示意图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示人民大会堂的点的坐标为(﹣2,0),表示王府井的点的坐标为(2,2),则表示故宫的点的坐标是
.
【解答】解:如图所示:故宫的点的坐标是:(﹣1,2).
故答案为:(﹣1,2).
三、解答题
15、如图,已知火车站的坐标为(2,2),文化宫的坐标为(-1,3).
(1)请你根据题目条件,画出平面直角坐标系;
(2)写出体育场,市场,超市的坐标;
(3)已知游乐场A,图书馆B,公园C的坐标分别为(0,5),(-2,-2),(2,-2),
请在图中标出A,B,C的位置.
解答:(1)如图
(2)体育场(-2,5)市场(6,5)超市(4,-1)
(3)如图
16、如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(2,1),图书馆位置坐标为B(-1,-2),解答以下问题:
(1)在图中试找出坐标系的原点,并建立直角坐标系;
(2)若体育馆位置坐标为C(1,-3),请在坐标系中标出体育馆的位置;
(3)顺次连结学校、图书馆、体育馆,得到三角形ABC,求三角形ABC的面积.
解:
(1)如图;
(2)如图;
(3)S△ABC=3×4-×2×1-×1×4-×3×3=4.5.
17、如图,点A,B在由若干个边长为1个单位长度的小正方形组成的网格图中,已知点A的坐标为
(-1,0),点B的坐标为(1,4),点C在x轴上,且AC=2.
(1)请在图中画出x轴、y轴及原点O;
(2)求点C的坐标,并画出△ABC;
(3)将△ABC的各顶点的横坐标和纵坐标都乘,得到△A1B1C1,求B1C1的长度.
解:(1)如图,
(2)点C坐标为(-3,0)或(1,0),△ABC如图所示.
(3)当点C坐标为(-3,0)时,B1C1=BC=×=2;
当点C坐标为(1,0)时,B1C1=BC=×4=2.
18、为了西部的发展,在某地区四个中小城市A,B,C,D附近新建机场E,若以A为原点建立直角坐标系,请用坐标来表示各城市及机场的位置.
解:若以A点为坐标原点,水平方向为x轴,竖直方向为y轴建立坐标系.
则各城市的坐标为:A(0,0),B(7,2),C(7,7),D(4,6),E(1,8).
19、图中标明了小英家附近的一些地方.以小英家为坐标原点,建立如图所示的坐标系.
(1)写出汽车站和消防站的坐标;
(2)某星期日早晨,小英同学从家里出发,沿(3,2),(3,-1),(0,-1),(-1,-2),(-3,-1)的路线转了一下,又回到家里,写出路上她经过的地方.
解:(1)汽车站(1,1),消防站(2,-2);
(2)小英路上经过的地方:游乐场,公园,姥姥家,宠物店,邮局.
巩固训练卷
一、选择题
1、在如图所示的象棋盘上,若“帅”和“相”所在的坐标分别是和上,则“炮”的坐标是
B.
C.
D.
2、如图,在的正方形网格中由四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是
A点
B.
B点
C.
C点
D.
D点
3、长方形ABCD的长为6,宽为4,建立平面直角坐标系如图所示,则下列各点中,不在这个长方形上的是(
)
A.
(3,2)
B.
(-2,-3)
C.
(0,2)
D.
(-3,2)
4、如图,在平面直角坐标系中,正方形OACB的顶点O,C的坐标分别是(0,0),(2,0),
则顶点B的坐标是(
)
A.(1,1)
B.(-1,-1)
C.(1,-1)
D.(-1,1)
5、设三角形三个顶点坐标分别为A(0,0),B(3,0),C(3,-3),则这个三角形是(
)
A.等边三角形
B.等腰直角三角形
C.钝角三角形
D.锐角三角形
6、如图,AB∥CD,AD∥BC∥x轴,下列说法正确的是(
)
A.A与D的横坐标相同
B.A与B的横坐标相同
C.B与C的纵坐标相同
D.C与D的纵坐标相同
7、等腰三角形ABC在直角坐标系中,底边的两端点坐标是(-2,0),(6,0),
则其顶点的坐标,能确定的是(
)
A.横坐标
B.纵坐标
C.横坐标及纵坐标
D.横坐标或纵坐标
8、如图,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),如果△ABD与△ABC全等,
那么点D的坐标是_________.
9、如图,在平面直角坐标系中,四边形ABCD的顶点A,B,C,D的坐标分别是(0,0),(5,0),(7,4),(2,4),
则这个四边形的面积是(
)
A.6
B.8
C.20
D.12
10、(2020?昌平区二模)昌平公园建成于1990年,公园内有一个占地10000平方米的静明湖,另外建有弘文阁、碑亭、文节亭、诗田亭、逸步桥、牌楼等园林景观及古建筑.如图,分别以正东、正北方向为x轴、y轴建立平面直角坐标系,如果表示文节亭的点的坐标为(2,0),表示园中园的点的坐标为(﹣1,2),则表示弘文阁所在的点的坐标为( )
A.(﹣2,﹣3)
B.(﹣2,﹣2)
C.(﹣3,﹣3)
D.(﹣3,﹣4)
二、填空题
11、课间操时,小颖、小浩的位置如图所示,小明对小浩说,如果我的位置用表示,小颖的位置用表示,那么小浩的位置可以表示成______
.
12、在方格纸上有两点A,B,若以B为原点建立直角坐标系,则点A的坐标为(4,3),若以A为原点建立直角坐标系,则点B的坐标为__________
13、如图是根据某公园的平面示意图建立的平面直角坐标系,公园的入口位于坐标原点O,古塔位于点,从古塔出发沿射线OA方向前行300m是盆景园B,从盆景园B向左转后直行400m到达梅花阁C,则点C的坐标是__?____
.
14、(2020春?延庆区期末)如图是天安门广场周围的景点分布示意图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示人民大会堂的点的坐标为(﹣2,0),表示王府井的点的坐标为(2,2),则表示故宫的点的坐标是
.
三、解答题
15、如图,已知火车站的坐标为(2,2),文化宫的坐标为(-1,3).
(1)请你根据题目条件,画出平面直角坐标系;
(2)写出体育场,市场,超市的坐标;
(3)已知游乐场A,图书馆B,公园C的坐标分别为(0,5),(-2,-2),(2,-2),
请在图中标出A,B,C的位置.
16、如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(2,1),图书馆位置坐标为B(-1,-2),解答以下问题:
(1)在图中试找出坐标系的原点,并建立直角坐标系;
(2)若体育馆位置坐标为C(1,-3),请在坐标系中标出体育馆的位置;
(3)顺次连结学校、图书馆、体育馆,得到三角形ABC,求三角形ABC的面积.
17、如图,点A,B在由若干个边长为1个单位长度的小正方形组成的网格图中,已知点A的坐标为
(-1,0),点B的坐标为(1,4),点C在x轴上,且AC=2.
(1)请在图中画出x轴、y轴及原点O;
(2)求点C的坐标,并画出△ABC;
(3)将△ABC的各顶点的横坐标和纵坐标都乘,得到△A1B1C1,求B1C1的长度.
18、为了西部的发展,在某地区四个中小城市A,B,C,D附近新建机场E,若以A为原点建立直角坐标系,请用坐标来表示各城市及机场的位置.
19、图中标明了小英家附近的一些地方.以小英家为坐标原点,建立如图所示的坐标系.
(1)写出汽车站和消防站的坐标;
(2)某星期日早晨,小英同学从家里出发,沿(3,2),(3,-1),(0,-1),(-1,-2),(-3,-1)的路线转了一下,又回到家里,写出路上她经过的地方.
2020-2021学年苏科版八年级上学期数学5.2平面直角坐标系(3)
巩固训练卷(答案)
一、选择题
1、在如图所示的象棋盘上,若“帅”和“相”所在的坐标分别是和上,则“炮”的坐标是
B.
C.
D.
解:如图所示:“帅”和“相”所在的坐标分别是和上,
“炮”的坐标是:.
故选:C.
2、如图,在的正方形网格中由四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是
A点
B.
B点
C.
C点
D.
D点
解:当以点B为原点时,,,
则点A和点C关于y轴对称,
符合条件,
故选:B
3、长方形ABCD的长为6,宽为4,建立平面直角坐标系如图所示,则下列各点中,不在这个长方形上的是(
B
)
A.
(3,2)
B.
(-2,-3)
C.
(0,2)
D.
(-3,2)
4、如图,在平面直角坐标系中,正方形OACB的顶点O,C的坐标分别是(0,0),(2,0),
则顶点B的坐标是(
C
)
A.(1,1)
B.(-1,-1)
C.(1,-1)
D.(-1,1)
5、设三角形三个顶点坐标分别为A(0,0),B(3,0),C(3,-3),则这个三角形是(
B
)
A.等边三角形
B.等腰直角三角形
C.钝角三角形
D.锐角三角形
6、如图,AB∥CD,AD∥BC∥x轴,下列说法正确的是(
C
)
A.A与D的横坐标相同
B.A与B的横坐标相同
C.B与C的纵坐标相同
D.C与D的纵坐标相同
7、等腰三角形ABC在直角坐标系中,底边的两端点坐标是(-2,0),(6,0),
则其顶点的坐标,能确定的是(
A
)
A.横坐标
B.纵坐标
C.横坐标及纵坐标
D.横坐标或纵坐标
8、如图,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),如果△ABD与△ABC全等,
那么点D的坐标是___(4,-1)或(-1,3)或(-1,-1)______.
9、如图,在平面直角坐标系中,四边形ABCD的顶点A,B,C,D的坐标分别是(0,0),(5,0),(7,4),(2,4),
则这个四边形的面积是(
C
)
A.6
B.8
C.20
D.12
10、(2020?昌平区二模)昌平公园建成于1990年,公园内有一个占地10000平方米的静明湖,另外建有弘文阁、碑亭、文节亭、诗田亭、逸步桥、牌楼等园林景观及古建筑.如图,分别以正东、正北方向为x轴、y轴建立平面直角坐标系,如果表示文节亭的点的坐标为(2,0),表示园中园的点的坐标为(﹣1,2),则表示弘文阁所在的点的坐标为( )
A.(﹣2,﹣3)
B.(﹣2,﹣2)
C.(﹣3,﹣3)
D.(﹣3,﹣4)
【解答】解:如图所示:弘文阁所在的点的坐标为:(﹣2,﹣2).
故选:B.
二、填空题
11、课间操时,小颖、小浩的位置如图所示,小明对小浩说,如果我的位置用表示,小颖的位置用表示,那么小浩的位置可以表示成__??____
.
12、在方格纸上有两点A,B,若以B为原点建立直角坐标系,则点A的坐标为(4,3),若以A为原点建立直角坐标系,则点B的坐标为____(-4,-3)______
13、如图是根据某公园的平面示意图建立的平面直角坐标系,公园的入口位于坐标原点O,古塔位于点,从古塔出发沿射线OA方向前行300m是盆景园B,从盆景园B向左转后直行400m到达梅花阁C,则点C的坐标是__?____
.
14、(2020春?延庆区期末)如图是天安门广场周围的景点分布示意图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示人民大会堂的点的坐标为(﹣2,0),表示王府井的点的坐标为(2,2),则表示故宫的点的坐标是
.
【解答】解:如图所示:故宫的点的坐标是:(﹣1,2).
故答案为:(﹣1,2).
三、解答题
15、如图,已知火车站的坐标为(2,2),文化宫的坐标为(-1,3).
(1)请你根据题目条件,画出平面直角坐标系;
(2)写出体育场,市场,超市的坐标;
(3)已知游乐场A,图书馆B,公园C的坐标分别为(0,5),(-2,-2),(2,-2),
请在图中标出A,B,C的位置.
解答:(1)如图
(2)体育场(-2,5)市场(6,5)超市(4,-1)
(3)如图
16、如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(2,1),图书馆位置坐标为B(-1,-2),解答以下问题:
(1)在图中试找出坐标系的原点,并建立直角坐标系;
(2)若体育馆位置坐标为C(1,-3),请在坐标系中标出体育馆的位置;
(3)顺次连结学校、图书馆、体育馆,得到三角形ABC,求三角形ABC的面积.
解:
(1)如图;
(2)如图;
(3)S△ABC=3×4-×2×1-×1×4-×3×3=4.5.
17、如图,点A,B在由若干个边长为1个单位长度的小正方形组成的网格图中,已知点A的坐标为
(-1,0),点B的坐标为(1,4),点C在x轴上,且AC=2.
(1)请在图中画出x轴、y轴及原点O;
(2)求点C的坐标,并画出△ABC;
(3)将△ABC的各顶点的横坐标和纵坐标都乘,得到△A1B1C1,求B1C1的长度.
解:(1)如图,
(2)点C坐标为(-3,0)或(1,0),△ABC如图所示.
(3)当点C坐标为(-3,0)时,B1C1=BC=×=2;
当点C坐标为(1,0)时,B1C1=BC=×4=2.
18、为了西部的发展,在某地区四个中小城市A,B,C,D附近新建机场E,若以A为原点建立直角坐标系,请用坐标来表示各城市及机场的位置.
解:若以A点为坐标原点,水平方向为x轴,竖直方向为y轴建立坐标系.
则各城市的坐标为:A(0,0),B(7,2),C(7,7),D(4,6),E(1,8).
19、图中标明了小英家附近的一些地方.以小英家为坐标原点,建立如图所示的坐标系.
(1)写出汽车站和消防站的坐标;
(2)某星期日早晨,小英同学从家里出发,沿(3,2),(3,-1),(0,-1),(-1,-2),(-3,-1)的路线转了一下,又回到家里,写出路上她经过的地方.
解:(1)汽车站(1,1),消防站(2,-2);
(2)小英路上经过的地方:游乐场,公园,姥姥家,宠物店,邮局.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
