人教版八年级数学下册18.1平行四边形同步测试(Word版,附答案)
文档属性
| 名称 | 人教版八年级数学下册18.1平行四边形同步测试(Word版,附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 150.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 00:00:00 | ||
图片预览



文档简介
18.1 平行四边形
一、选择题(每小题4分,共28分)
1.如图1,若平行四边形ABCD的周长是28
cm,△ABC的周长是22
cm,则AC的长为( )
图1
A.6
cm
B.12
cm
C.4
cm
D.8
cm
2.下列命题中,不正确的是
( )
A.两组对边分别平行的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行,另一组对边相等的四边形是平行四边形
D.对角线互相平分的四边形是平行四边形
3.如图2,已知?ABCD,根据图中尺规作图的痕迹,判断下列结论中不一定成立的是( )
图2
A.∠DAE=∠BAE
B.∠DEA=∠DAB
C.DE=BE
D.BC=DE
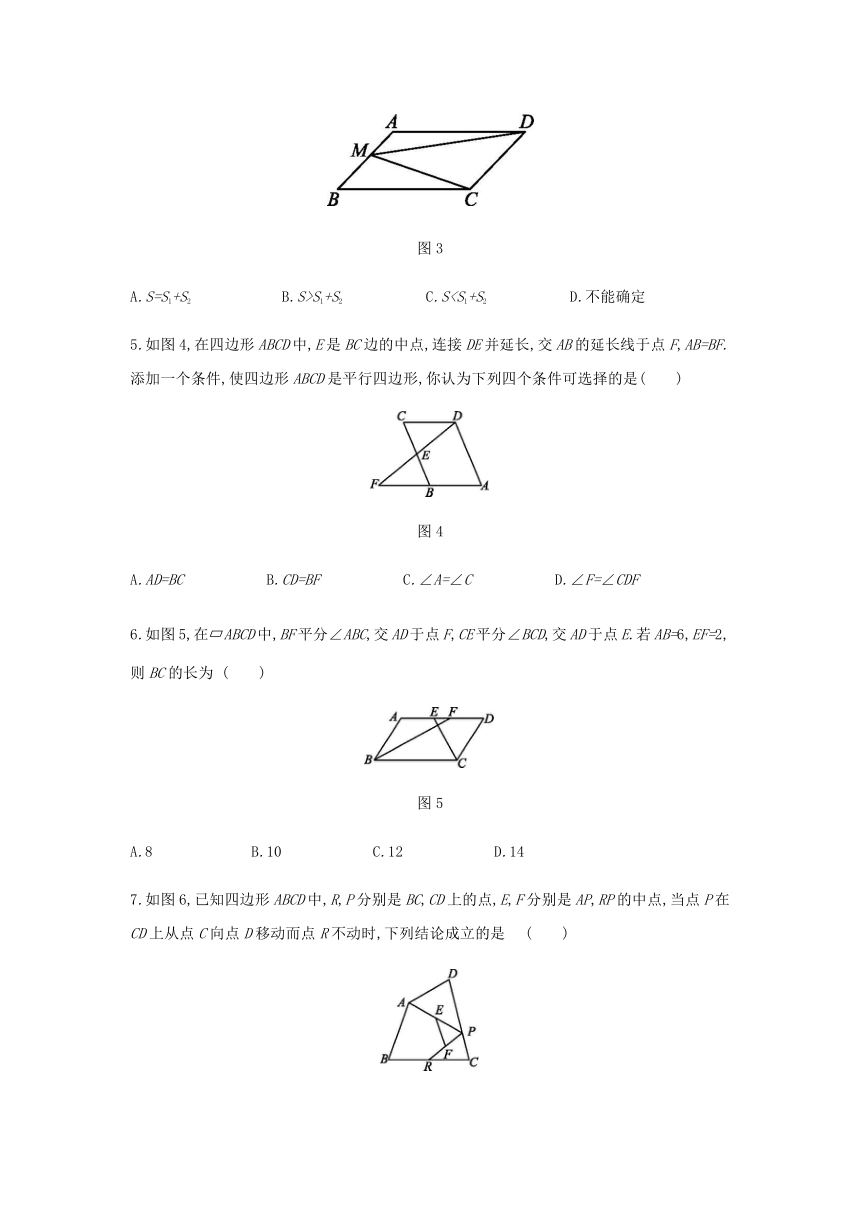
4.如图3,M为?ABCD的边AB上任意一点,设△AMD的面积为S1,△BMC的面积为S2,△CDM的面积为S,则
( )
图3
A.S=S1+S2
B.S>S1+S2
C.SD.不能确定
5.如图4,在四边形ABCD中,E是BC边的中点,连接DE并延长,交AB的延长线于点F,AB=BF.添加一个条件,使四边形ABCD是平行四边形,你认为下列四个条件可选择的是( )
图4
A.AD=BC
B.CD=BF
C.∠A=∠C
D.∠F=∠CDF
6.如图5,在?ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E.若AB=6,EF=2,则BC的长为
( )
图5
A.8
B.10
C.12
D.14
7.如图6,已知四边形ABCD中,R,P分别是BC,CD上的点,E,F分别是AP,RP的中点,当点P在CD上从点C向点D移动而点R不动时,下列结论成立的是
( )
图6
A.线段EF的长度逐渐增大
B.线段EF的长度逐渐减小
C.线段EF的长度不变
D.线段EF的长度与点P的位置有关
二、填空题(每小题4分,共24分)
8.如图7所示,在?ABCD中,BD是对角线,E,F是BD上的点,且BE=DF,请写出图中的一对全等三角形: .?
图7
9.在四边形ABCD中,给出下列条件:①AB∥CD;②AD=BC;③∠A=∠C;④AD∥BC.选其中两个条件就能判定四边形ABCD是平行四边形的所有组合是 (填序号).?
10.如图8,在四边形ABCD中,两条对角线AC,BD相交于点O,且OA=OC,OB=OD.若△ABO的面积是3,则?ABCD的面积为 .?
图8
11.如图9,CD是△ABC的中线,E,F分别是AC,DC的中点,EF=1,则BD= .?
图9
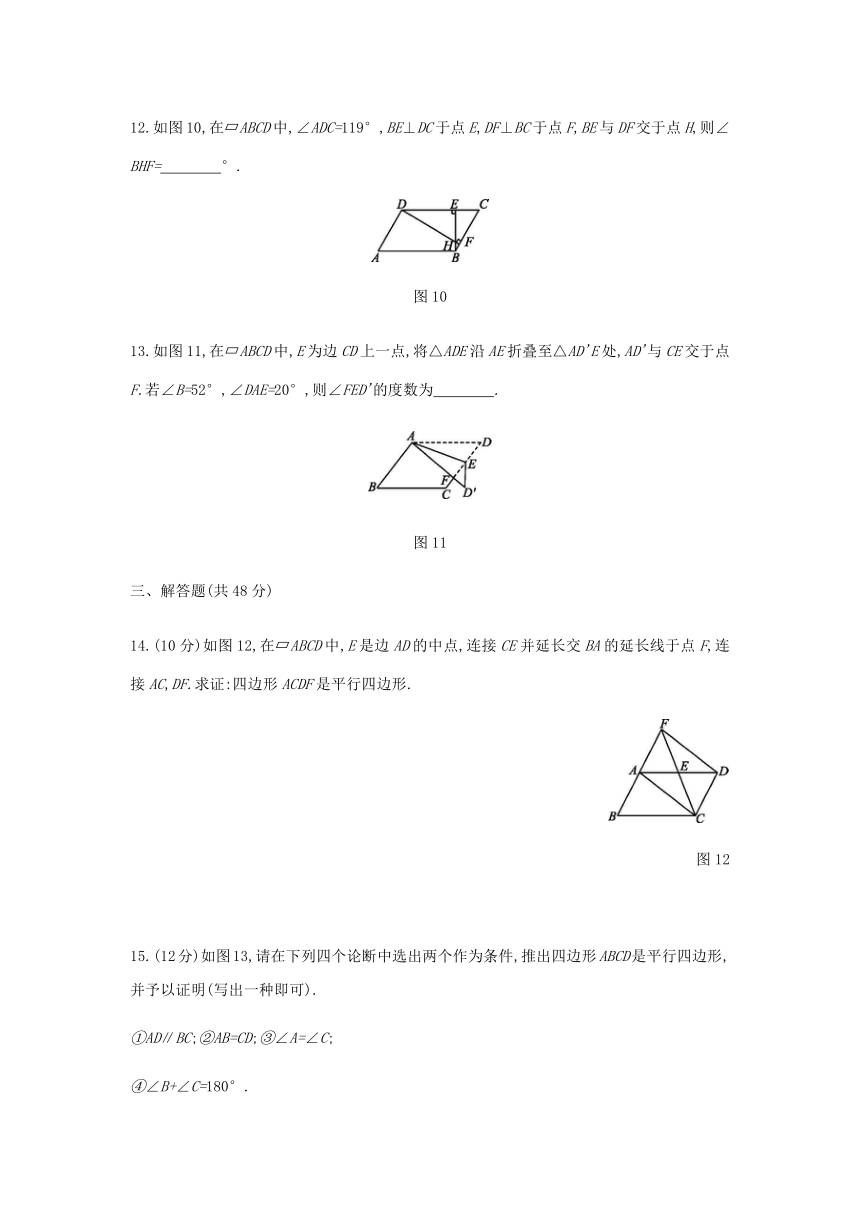
12.如图10,在?ABCD中,∠ADC=119°,BE⊥DC于点E,DF⊥BC于点F,BE与DF交于点H,则∠BHF= °.?
图10
13.如图11,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD'E处,AD'与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED'的度数为 .?
图11
三、解答题(共48分)
14.(10分)如图12,在?ABCD中,E是边AD的中点,连接CE并延长交BA的延长线于点F,连接AC,DF.求证:四边形ACDF是平行四边形.
图12
15.(12分)如图13,请在下列四个论断中选出两个作为条件,推出四边形ABCD是平行四边形,并予以证明(写出一种即可).
①AD∥BC;②AB=CD;③∠A=∠C;
④∠B+∠C=180°.
已知:在四边形ABCD中, .?
求证:四边形ABCD是平行四边形.
图13
16.(12分)如图14,已知点A,C在EF上,AD∥BC,DE∥BF,AE=CF.
(1)求证:四边形ABCD是平行四边形;
(2)直接写出图中所有相等的线段(AE=CF除外).
图14
17.(14分)如图15,在Rt△ABC中,∠B=90°,AC=60
cm,∠A=60°,点D从点C出发沿CA方向以4
cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2
cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t
s(0(1)求证:四边形AEFD是平行四边形;
(2)当t为何值时,△DEF为直角三角形?
图15
答案
1.D [解析]
根据平行四边形的对边相等可得AB+BC=×28=14(cm).又△ABC的周长是22
cm,所以AC=22-14=8(cm).
2.C
3.C [解析]
A选项,由作法可知AE平分∠DAB,∴∠DAE=∠BAE,故本选项不符合题意;
B选项,∵CD∥AB,∴∠DEA=∠BAE=∠DAB=∠DAE,故本选项不符合题意;
C选项,无法证明DE=BE,故本选项符合题意;
D选项,∵∠DAE=∠DEA,∴AD=DE.又∵AD=BC,∴BC=DE,故本选项不符合题意.
4.A
5.D [解析]
题干中有AB=BF,因此证AB∥CD,AB=CD即可,而要证这两个条件应证△BEF≌△CED.结合题干中条件:E为BC的中点,又有对顶角,因此添加∠F=∠CDF可证△BEF≌△CED,可得AB∥CD,AB=CD.
6.B [解析]
∵四边形ABCD是平行四边形,
∴AD∥BC,DC=AB=6,AD=BC,
∴∠AFB=∠FBC.
∵BF平分∠ABC,∴∠ABF=∠FBC,
则∠ABF=∠AFB,∴AF=AB=6.
同理可得:DE=DC=6.
∵EF=AF+DE-AD=2,
即6+6-AD=2,解得AD=10.故BC=10.
故选B.
7.C [解析]
如图,连接AR,则EF是△APR的中位线,EF=AR.因为在点P的移动过程中,点A和点R的位置不变,所以AR的长度不变.因此,线段EF的长度也不变.
8.△AFD≌△CEB,△BAF≌△DCE,△ABD≌△CDB(答案不唯一,选其中一对即可)
9.①③,①④,②④,③④
10.12 [解析]
∵OA=OC,
∴S△ABO=S△CBO=3,
∴S?ABCD=2S△ABC=4S△ABO=12.
11.2
12.61 [解析]
∵四边形ABCD是平行四边形,
∴AD∥BC,DC∥AB.
∵∠ADC=119°,DF⊥BC,
∴∠ADF=90°,
则∠EDH=29°,
∵BE⊥DC,
∴∠DEH=90°,
∴∠DHE=∠BHF=90°-29°=61°.
故答案为61.
13.36° [解析]
∵四边形ABCD是平行四边形,
∴∠D=∠B=52°.
由折叠的性质得:∠D'=∠D=52°,∠EAD'=∠DAE=20°,
∴∠AEF=∠D+∠DAE=52°+20°=72°,∠AED'=180°-∠EAD'-∠D'=108°,
∴∠FED'=108°-72°=36°.
14.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠FAE=∠CDE.
∵E是AD的中点,
∴AE=DE.
又∵∠FEA=∠CED,
∴△FAE≌△CDE(ASA),
∴CD=FA.
又∵CD∥FA,
∴四边形ACDF是平行四边形.
15.解:答案不唯一,选以下解法中的一个即可.
解法一:
已知:在四边形ABCD中,①AD∥BC,③∠A=∠C.
求证:四边形ABCD是平行四边形.
证明:∵AD∥BC,
∴∠A+∠B=180°,∠C+∠D=180°.
∵∠A=∠C,∴∠B=∠D,
∴四边形ABCD是平行四边形.
解法二:
已知:在四边形ABCD中,①AD∥BC,④∠B+∠C=180°.
求证:四边形ABCD是平行四边形.
证明:∵∠B+∠C=180°,∴AB∥CD.
又∵AD∥BC,
∴四边形ABCD是平行四边形.
解法三:
已知:在四边形ABCD中,②AB=CD,④∠B+∠C=180°.
求证:四边形ABCD是平行四边形.
证明:∵∠B+∠C=180°,∴AB∥CD.
又∵AB=CD,
∴四边形ABCD是平行四边形.
解法四:
已知:在四边形ABCD中,③∠A=∠C,④∠B+∠C=180°.
求证:四边形ABCD是平行四边形.
证明:∵∠B+∠C=180°,
∴AB∥CD,∴∠A+∠D=180°.
∵∠A=∠C,∴∠B=∠D,
∴四边形ABCD是平行四边形.
16.解:(1)证明:∵AD∥BC,DE∥BF,∴∠E=∠F,∠DAC=∠BCA,∴∠DAE=∠BCF.
在△ADE和△CBF中,
∴△ADE≌△CBF(ASA),∴AD=BC.
又AD∥BC,∴四边形ABCD是平行四边形.
(2)AD=BC,EC=AF,ED=BF,AB=DC.
17.解:(1)证明:∵∠B=90°,∠A=60°,
∴∠C=30°,
∴AB=AC=30
cm.
由题意,得CD=4t
cm,AE=2t
cm.
∵DF⊥BC,∠C=30°,
∴DF=CD=2t
cm,
∴DF=AE.
∵DF⊥BC,∠B=90°,∴DF∥AE,
∴四边形AEFD是平行四边形.
(2)若∠EDF=90°,如图①.
又∵DF⊥BC,∴DE∥BC,
∴∠ADE=∠C=30°,∠AED=∠B=90°,
∴AD=2AE,即60-4t=2t×2,
解得t=.
若∠DEF=90°,如图②.
∵四边形AEFD是平行四边形,∴AD∥EF,
∴DE⊥AC.
又∵∠A=60°,∴∠AED=30°,
∴AE=2AD,即2t=2×(60-4t),
解得t=12.
综上所述,当t=或t=12时,△DEF为直角三角形.
一、选择题(每小题4分,共28分)
1.如图1,若平行四边形ABCD的周长是28
cm,△ABC的周长是22
cm,则AC的长为( )
图1
A.6
cm
B.12
cm
C.4
cm
D.8
cm
2.下列命题中,不正确的是
( )
A.两组对边分别平行的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行,另一组对边相等的四边形是平行四边形
D.对角线互相平分的四边形是平行四边形
3.如图2,已知?ABCD,根据图中尺规作图的痕迹,判断下列结论中不一定成立的是( )
图2
A.∠DAE=∠BAE
B.∠DEA=∠DAB
C.DE=BE
D.BC=DE
4.如图3,M为?ABCD的边AB上任意一点,设△AMD的面积为S1,△BMC的面积为S2,△CDM的面积为S,则
( )
图3
A.S=S1+S2
B.S>S1+S2
C.S
5.如图4,在四边形ABCD中,E是BC边的中点,连接DE并延长,交AB的延长线于点F,AB=BF.添加一个条件,使四边形ABCD是平行四边形,你认为下列四个条件可选择的是( )
图4
A.AD=BC
B.CD=BF
C.∠A=∠C
D.∠F=∠CDF
6.如图5,在?ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E.若AB=6,EF=2,则BC的长为
( )
图5
A.8
B.10
C.12
D.14
7.如图6,已知四边形ABCD中,R,P分别是BC,CD上的点,E,F分别是AP,RP的中点,当点P在CD上从点C向点D移动而点R不动时,下列结论成立的是
( )
图6
A.线段EF的长度逐渐增大
B.线段EF的长度逐渐减小
C.线段EF的长度不变
D.线段EF的长度与点P的位置有关
二、填空题(每小题4分,共24分)
8.如图7所示,在?ABCD中,BD是对角线,E,F是BD上的点,且BE=DF,请写出图中的一对全等三角形: .?
图7
9.在四边形ABCD中,给出下列条件:①AB∥CD;②AD=BC;③∠A=∠C;④AD∥BC.选其中两个条件就能判定四边形ABCD是平行四边形的所有组合是 (填序号).?
10.如图8,在四边形ABCD中,两条对角线AC,BD相交于点O,且OA=OC,OB=OD.若△ABO的面积是3,则?ABCD的面积为 .?
图8
11.如图9,CD是△ABC的中线,E,F分别是AC,DC的中点,EF=1,则BD= .?
图9
12.如图10,在?ABCD中,∠ADC=119°,BE⊥DC于点E,DF⊥BC于点F,BE与DF交于点H,则∠BHF= °.?
图10
13.如图11,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD'E处,AD'与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED'的度数为 .?
图11
三、解答题(共48分)
14.(10分)如图12,在?ABCD中,E是边AD的中点,连接CE并延长交BA的延长线于点F,连接AC,DF.求证:四边形ACDF是平行四边形.
图12
15.(12分)如图13,请在下列四个论断中选出两个作为条件,推出四边形ABCD是平行四边形,并予以证明(写出一种即可).
①AD∥BC;②AB=CD;③∠A=∠C;
④∠B+∠C=180°.
已知:在四边形ABCD中, .?
求证:四边形ABCD是平行四边形.
图13
16.(12分)如图14,已知点A,C在EF上,AD∥BC,DE∥BF,AE=CF.
(1)求证:四边形ABCD是平行四边形;
(2)直接写出图中所有相等的线段(AE=CF除外).
图14
17.(14分)如图15,在Rt△ABC中,∠B=90°,AC=60
cm,∠A=60°,点D从点C出发沿CA方向以4
cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2
cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t
s(0
(2)当t为何值时,△DEF为直角三角形?
图15
答案
1.D [解析]
根据平行四边形的对边相等可得AB+BC=×28=14(cm).又△ABC的周长是22
cm,所以AC=22-14=8(cm).
2.C
3.C [解析]
A选项,由作法可知AE平分∠DAB,∴∠DAE=∠BAE,故本选项不符合题意;
B选项,∵CD∥AB,∴∠DEA=∠BAE=∠DAB=∠DAE,故本选项不符合题意;
C选项,无法证明DE=BE,故本选项符合题意;
D选项,∵∠DAE=∠DEA,∴AD=DE.又∵AD=BC,∴BC=DE,故本选项不符合题意.
4.A
5.D [解析]
题干中有AB=BF,因此证AB∥CD,AB=CD即可,而要证这两个条件应证△BEF≌△CED.结合题干中条件:E为BC的中点,又有对顶角,因此添加∠F=∠CDF可证△BEF≌△CED,可得AB∥CD,AB=CD.
6.B [解析]
∵四边形ABCD是平行四边形,
∴AD∥BC,DC=AB=6,AD=BC,
∴∠AFB=∠FBC.
∵BF平分∠ABC,∴∠ABF=∠FBC,
则∠ABF=∠AFB,∴AF=AB=6.
同理可得:DE=DC=6.
∵EF=AF+DE-AD=2,
即6+6-AD=2,解得AD=10.故BC=10.
故选B.
7.C [解析]
如图,连接AR,则EF是△APR的中位线,EF=AR.因为在点P的移动过程中,点A和点R的位置不变,所以AR的长度不变.因此,线段EF的长度也不变.
8.△AFD≌△CEB,△BAF≌△DCE,△ABD≌△CDB(答案不唯一,选其中一对即可)
9.①③,①④,②④,③④
10.12 [解析]
∵OA=OC,
∴S△ABO=S△CBO=3,
∴S?ABCD=2S△ABC=4S△ABO=12.
11.2
12.61 [解析]
∵四边形ABCD是平行四边形,
∴AD∥BC,DC∥AB.
∵∠ADC=119°,DF⊥BC,
∴∠ADF=90°,
则∠EDH=29°,
∵BE⊥DC,
∴∠DEH=90°,
∴∠DHE=∠BHF=90°-29°=61°.
故答案为61.
13.36° [解析]
∵四边形ABCD是平行四边形,
∴∠D=∠B=52°.
由折叠的性质得:∠D'=∠D=52°,∠EAD'=∠DAE=20°,
∴∠AEF=∠D+∠DAE=52°+20°=72°,∠AED'=180°-∠EAD'-∠D'=108°,
∴∠FED'=108°-72°=36°.
14.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠FAE=∠CDE.
∵E是AD的中点,
∴AE=DE.
又∵∠FEA=∠CED,
∴△FAE≌△CDE(ASA),
∴CD=FA.
又∵CD∥FA,
∴四边形ACDF是平行四边形.
15.解:答案不唯一,选以下解法中的一个即可.
解法一:
已知:在四边形ABCD中,①AD∥BC,③∠A=∠C.
求证:四边形ABCD是平行四边形.
证明:∵AD∥BC,
∴∠A+∠B=180°,∠C+∠D=180°.
∵∠A=∠C,∴∠B=∠D,
∴四边形ABCD是平行四边形.
解法二:
已知:在四边形ABCD中,①AD∥BC,④∠B+∠C=180°.
求证:四边形ABCD是平行四边形.
证明:∵∠B+∠C=180°,∴AB∥CD.
又∵AD∥BC,
∴四边形ABCD是平行四边形.
解法三:
已知:在四边形ABCD中,②AB=CD,④∠B+∠C=180°.
求证:四边形ABCD是平行四边形.
证明:∵∠B+∠C=180°,∴AB∥CD.
又∵AB=CD,
∴四边形ABCD是平行四边形.
解法四:
已知:在四边形ABCD中,③∠A=∠C,④∠B+∠C=180°.
求证:四边形ABCD是平行四边形.
证明:∵∠B+∠C=180°,
∴AB∥CD,∴∠A+∠D=180°.
∵∠A=∠C,∴∠B=∠D,
∴四边形ABCD是平行四边形.
16.解:(1)证明:∵AD∥BC,DE∥BF,∴∠E=∠F,∠DAC=∠BCA,∴∠DAE=∠BCF.
在△ADE和△CBF中,
∴△ADE≌△CBF(ASA),∴AD=BC.
又AD∥BC,∴四边形ABCD是平行四边形.
(2)AD=BC,EC=AF,ED=BF,AB=DC.
17.解:(1)证明:∵∠B=90°,∠A=60°,
∴∠C=30°,
∴AB=AC=30
cm.
由题意,得CD=4t
cm,AE=2t
cm.
∵DF⊥BC,∠C=30°,
∴DF=CD=2t
cm,
∴DF=AE.
∵DF⊥BC,∠B=90°,∴DF∥AE,
∴四边形AEFD是平行四边形.
(2)若∠EDF=90°,如图①.
又∵DF⊥BC,∴DE∥BC,
∴∠ADE=∠C=30°,∠AED=∠B=90°,
∴AD=2AE,即60-4t=2t×2,
解得t=.
若∠DEF=90°,如图②.
∵四边形AEFD是平行四边形,∴AD∥EF,
∴DE⊥AC.
又∵∠A=60°,∴∠AED=30°,
∴AE=2AD,即2t=2×(60-4t),
解得t=12.
综上所述,当t=或t=12时,△DEF为直角三角形.
