3.2圆的对称性2课件
图片预览



文档简介
(共14张PPT)
3.2 圆的对称性(2)
济宁十二中 陈伟利
做一做
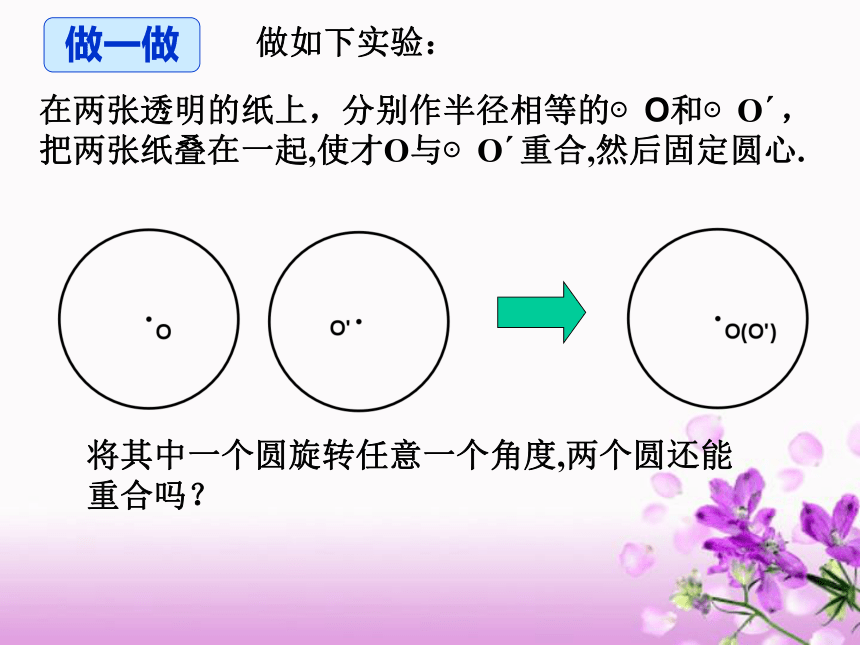
做如下实验:
在两张透明的纸上,分别作半径相等的⊙O和⊙O ,把两张纸叠在一起,使才O与⊙O 重合,然后固定圆心.
将其中一个圆旋转任意一个角度,两个圆还能重合吗?
利用旋转的方法可以得到:一个圆绕着它的圆心旋转任意一个角度,都能与原图形重合.这叫做圆的旋转不变性.
特别地
圆是中心对称图形,对称中心是圆心.
做一做
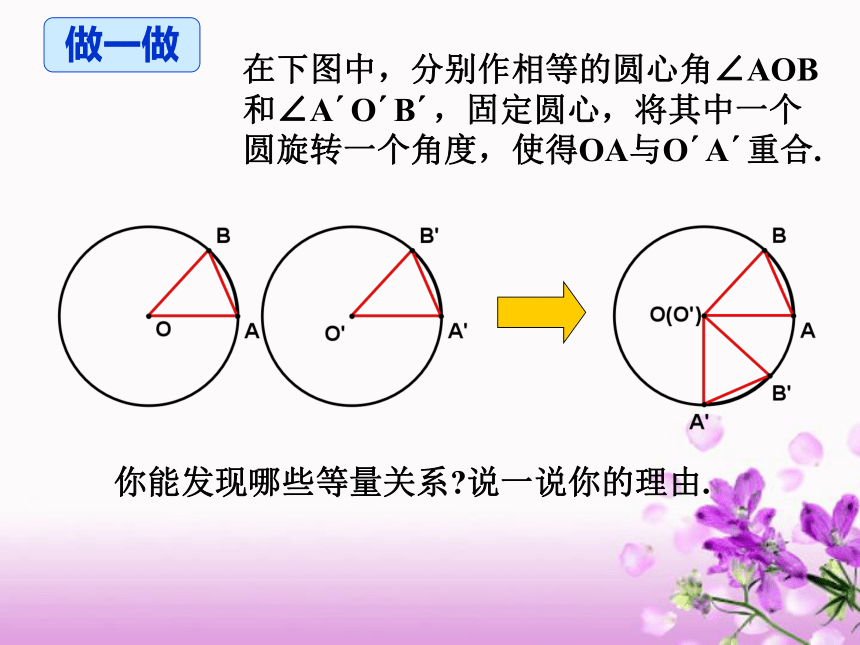
在下图中,分别作相等的圆心角∠AOB和∠A O B ,固定圆心,将其中一个圆旋转一个角度,使得OA与O A 重合.
你能发现哪些等量关系 说一说你的理由.
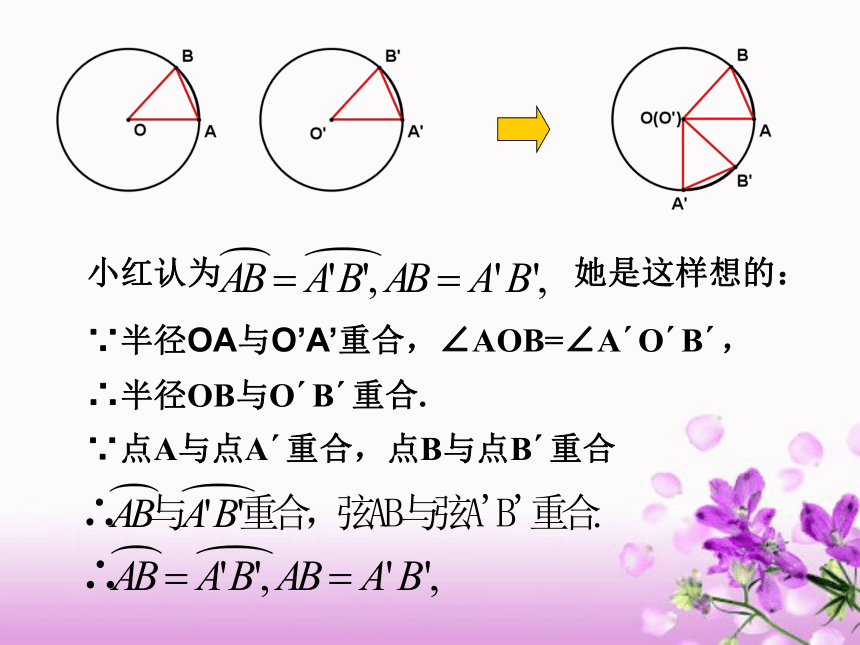
小红认为
她是这样想的:
∵半径OA与O’A’重合,∠AOB=∠A O B ,
∴半径OB与O B 重合.
∵点A与点A 重合,点B与点B 重合
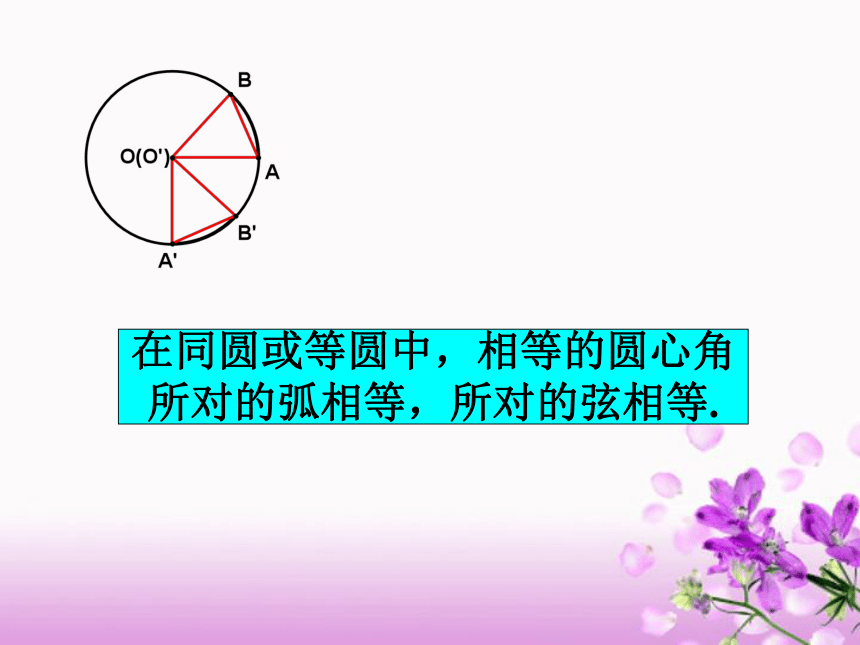
在同圆或等圆中,相等的圆心角
所对的弧相等,所对的弦相等.
想一想
在同圆或等圆中,如果两个圆心角所对的弧相等,那么它们所对的弦相等吗?
它们所对的圆心角相等吗?
你是怎么想的?
如果弦相等,你又能得到什么结论?
在同圆或等圆中,如果两个圆心角、两条弧、
两条弦中有一组量相等,那么它们所对应的其余
各组量都分别相等.
例1:如图,在⊙O中,AB、CD是两条弦OE⊥AB,OF⊥CD,垂足分别为E、F.
(1) 如果∠AOB = ∠COD ,那么OE与OF的大小有什么关系?为什么?
解: (1) 如果∠AOB = ∠COD ,那么OE=OF
∵ ∠AOB = ∠COD
∴AB=CD
∵ OE⊥AB,OF⊥CD
∴
∴AE=CF
又∵OA=OC
∴Rt△OAE≌Rt△OCF
∴ OE=OF
例1:如图,在⊙O中,AB、CD是两条弦OE⊥AB,OF⊥CD,垂足分别为E、F.
(2) 如果OE=OF,那么AB与CD的大小有什么关系?为什么?
与 的大小有什么关系?
为什么?
∠AOB 与∠COD呢?
(2) 如果OE=OF,那么AB=CD,
=
,∠AOB =∠COD
∵OA=OC, OE=OF
∴Rt△OAE≌Rt△OCF
∴AE=CF
又∵ OE⊥AB,OF⊥CD
∴
∴AB=2AE,CD=2CF
∴AB=CD
,∠AOB =∠COD
=
∴
议一议
在得到本节结论的过程中,你用到了哪些方法?与同伴进行交流.
折叠(轴对称)
旋转
证明
随堂练习
1.日常生活中的许多图案或现象都与圆的对称性有关,试举几例.
2.利用一个圆及其若干条弦分别设计出符合下列条件的图案:
(1)是轴对称图形但不是中心对称图形;
(2)既是轴对称图形又是中心对称图形.
随堂练习
3.已知A、B是⊙O上的两点, ∠AOB =120°,C是 的中点,试确定四边形OACB的形状,并说明理由.
随堂练习
4。A、B、C、D是⊙ O上的四点,AB=DC, △ABC与△DCB全等吗?为什么?
3.2 圆的对称性(2)
济宁十二中 陈伟利
做一做
做如下实验:
在两张透明的纸上,分别作半径相等的⊙O和⊙O ,把两张纸叠在一起,使才O与⊙O 重合,然后固定圆心.
将其中一个圆旋转任意一个角度,两个圆还能重合吗?
利用旋转的方法可以得到:一个圆绕着它的圆心旋转任意一个角度,都能与原图形重合.这叫做圆的旋转不变性.
特别地
圆是中心对称图形,对称中心是圆心.
做一做
在下图中,分别作相等的圆心角∠AOB和∠A O B ,固定圆心,将其中一个圆旋转一个角度,使得OA与O A 重合.
你能发现哪些等量关系 说一说你的理由.
小红认为
她是这样想的:
∵半径OA与O’A’重合,∠AOB=∠A O B ,
∴半径OB与O B 重合.
∵点A与点A 重合,点B与点B 重合
在同圆或等圆中,相等的圆心角
所对的弧相等,所对的弦相等.
想一想
在同圆或等圆中,如果两个圆心角所对的弧相等,那么它们所对的弦相等吗?
它们所对的圆心角相等吗?
你是怎么想的?
如果弦相等,你又能得到什么结论?
在同圆或等圆中,如果两个圆心角、两条弧、
两条弦中有一组量相等,那么它们所对应的其余
各组量都分别相等.
例1:如图,在⊙O中,AB、CD是两条弦OE⊥AB,OF⊥CD,垂足分别为E、F.
(1) 如果∠AOB = ∠COD ,那么OE与OF的大小有什么关系?为什么?
解: (1) 如果∠AOB = ∠COD ,那么OE=OF
∵ ∠AOB = ∠COD
∴AB=CD
∵ OE⊥AB,OF⊥CD
∴
∴AE=CF
又∵OA=OC
∴Rt△OAE≌Rt△OCF
∴ OE=OF
例1:如图,在⊙O中,AB、CD是两条弦OE⊥AB,OF⊥CD,垂足分别为E、F.
(2) 如果OE=OF,那么AB与CD的大小有什么关系?为什么?
与 的大小有什么关系?
为什么?
∠AOB 与∠COD呢?
(2) 如果OE=OF,那么AB=CD,
=
,∠AOB =∠COD
∵OA=OC, OE=OF
∴Rt△OAE≌Rt△OCF
∴AE=CF
又∵ OE⊥AB,OF⊥CD
∴
∴AB=2AE,CD=2CF
∴AB=CD
,∠AOB =∠COD
=
∴
议一议
在得到本节结论的过程中,你用到了哪些方法?与同伴进行交流.
折叠(轴对称)
旋转
证明
随堂练习
1.日常生活中的许多图案或现象都与圆的对称性有关,试举几例.
2.利用一个圆及其若干条弦分别设计出符合下列条件的图案:
(1)是轴对称图形但不是中心对称图形;
(2)既是轴对称图形又是中心对称图形.
随堂练习
3.已知A、B是⊙O上的两点, ∠AOB =120°,C是 的中点,试确定四边形OACB的形状,并说明理由.
随堂练习
4。A、B、C、D是⊙ O上的四点,AB=DC, △ABC与△DCB全等吗?为什么?
