人教版2020年八年级数学上册课时作业本 13.3.1轴对称与等腰三角形-等腰三角形性质与判定(word含答案)
文档属性
| 名称 | 人教版2020年八年级数学上册课时作业本 13.3.1轴对称与等腰三角形-等腰三角形性质与判定(word含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 108.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 00:00:00 | ||
图片预览



文档简介
人教版2020年八年级数学上册课时作业本
轴对称与等腰三角形-等腰三角形性质与判定
、选择题
一个等腰三角形的两边长分别为4,8,则它的周长为(
)
A.12
B.16
C.20
D.16或20
等腰三角形的一条边长为6,另一边长为13,则它的周长为(
)
A.25
B.25或32
C.32
D.19
如图,在△ABC中,AB=AC=4,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC分别交AB、AC于M、N,则△AMN的周长为(
)
A.12
B.4
C.8
D.不确定
如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为(
)
A.BD=CE
B.AD=AE
C.DA=DE
D.BE=CD
若等腰三角形的顶角为40°,则它的底角度数为(
)
A.40°
B.50°
C.60°
D.70°
如果等腰三角形的一个底角为α,那么(
)
A.α不大于45°
B.0°<α<90°
C.α不大于90°
D.45°<α<90°
如图,MN是线段AB的垂直平分线,C在MN外,且与A点在MN的同一侧,BC交MN于P点,则(
)
A.BC>PC+AP
B.BC<PC+AP
C.BC=PC+AP
D.BC≥PC+AP
如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF的度数为(
)
A.48°
B.36°
C.30°
D.24°
如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于(
)
A.110°
B.120°
C.130°
D.140°
如图,已知下列三角形中,AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( )
A.①③④
B.①②③④
C.①②④
D.①③
、填空题
一个等腰三角形的一个角为80°,则它的顶角的度数是 .
已知一个等腰三角形两内角的度数之比为1:4,则这个等腰三角形顶角的度数为 .
若等腰三角形的一个外角为70°,则它的底角为
度.
已知等腰三角形的顶角为40°,则它一腰上的高与底边的夹角为
.
如图,在△ABC中,AB=AC,AD⊥BC于D点,点E、F分别是AD的三等分点,若△ABC的面积为18cm2,则图中阴影部分面积为
cm2.
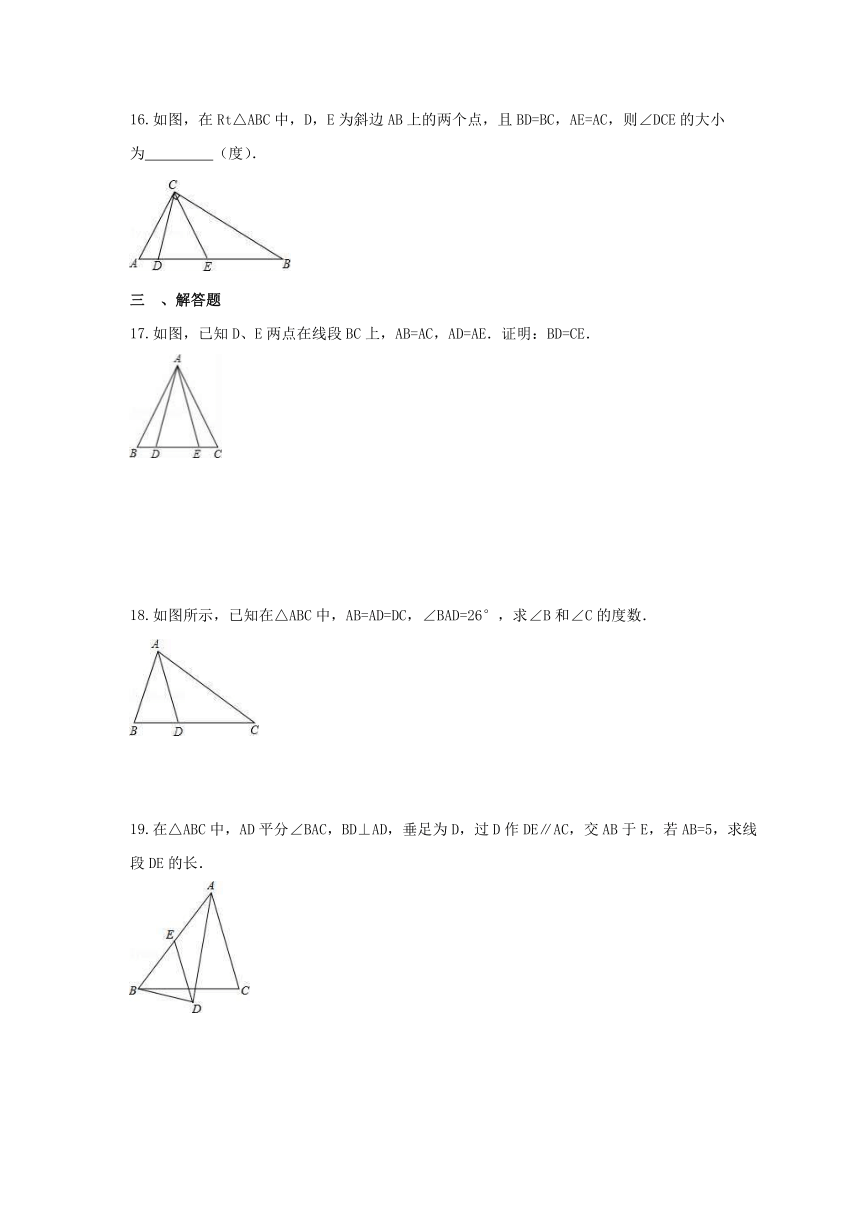
如图,在Rt△ABC中,D,E为斜边AB上的两个点,且BD=BC,AE=AC,则∠DCE的大小
为
(度).
、解答题
如图,已知D、E两点在线段BC上,AB=AC,AD=AE.证明:BD=CE.
如图所示,已知在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E,若AB=5,求线段DE的长.
如图,△ABC中BD、CD平分∠ABC、∠ACB,过D作直线平行于BC,交AB、AC于E、F,求证:EF=BE+CF.
如图,在△ABC中,AB=AC,D、E分别在AC、AB边上,且BC=BD,AD=DE=EB,求∠A的度数.
如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(1)求证:BE=CE;
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其它条件不变.求证:△AEF≌△BCF.
参考答案
C
C
C
C
D
B
C
A
答案为:A.
A.
答案为:80°或20°.
答案为:120°或20°.
答案为:35.
答案为:20°.
答案为:9.
答案为:45.
证明:
过A作AF⊥BC于F,
∵AB=AC,AD=AE,AF⊥BC,
∴BF=CF,DF=EF,
∴BF﹣DF=CF﹣EF,
∴BD=CE.
解:在△ABC中,AB=AD=DC,
∵AB=AD,在三角形ABD中,
∠B=∠ADB=(180°﹣26°)×=77°,
又∵AD=DC,在三角形ADC中,
∴∠C==77°×=38.5°.
解:∵AD平分∠BAC,∴∠BAD=∠CAD,
∵DE∥AC,∴∠CAD=∠ADE,∴∠BAD=∠ADE,∴AE=DE,
∵AD⊥DB,∴∠ADB=90°,
∴∠EAD+∠ABD=90°,∠ADE+∠BDE=∠ADB=90°,
∴∠ABD=∠BDE,∴DE=BE,
∵AB=5,∴DE=BE=AE==2.5.
解:∵△ABC中BD、CD平分∠ABC、∠ACB,
∴∠1=∠2,∠5=∠6,
∵EF∥BC,∴∠2=∠3,∠4=∠6,
∴∠1=∠3,∠4=∠5,
根据在同一三角形中等角对等边的原则可知,BE=ED,DF=FC,
故EF=ED+DF=BE+CF.
解:∵DE=EB∴设∠BDE=∠ABD=x,
∴∠AED=∠BDE+∠ABD=2x,
∵AD=DE,∴∠AED=∠A=2x,
∴∠BDC=∠A+∠ABD=3x,
∵BD=BC,
∴∠C=∠BDC=3x,
∵AB=AC,
∴∠ABC=∠C=3x,
在△ABC中,3x+3x+2x=180°,解得x=22.5°,
∴∠A=2x=22.5°×2=45°.
证明:(1)∵AB=AC,D是BC的中点,
∴∠BAE=∠EAC,
在△ABE和△ACE中,,
∴△ABE≌△ACE(SAS),
∴BE=CE;
(2)∵∠BAC=45°,BF⊥AF,
∴△ABF为等腰直角三角形,
∴AF=BF,
∵AB=AC,点D是BC的中点,
∴AD⊥BC,
∴∠EAF+∠C=90°,
∵BF⊥AC,
∴∠CBF+∠C=90°,
∴∠EAF=∠CBF,
在△AEF和△BCF中,,
∴△AEF≌△BCF(ASA).
轴对称与等腰三角形-等腰三角形性质与判定
、选择题
一个等腰三角形的两边长分别为4,8,则它的周长为(
)
A.12
B.16
C.20
D.16或20
等腰三角形的一条边长为6,另一边长为13,则它的周长为(
)
A.25
B.25或32
C.32
D.19
如图,在△ABC中,AB=AC=4,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC分别交AB、AC于M、N,则△AMN的周长为(
)
A.12
B.4
C.8
D.不确定
如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为(
)
A.BD=CE
B.AD=AE
C.DA=DE
D.BE=CD
若等腰三角形的顶角为40°,则它的底角度数为(
)
A.40°
B.50°
C.60°
D.70°
如果等腰三角形的一个底角为α,那么(
)
A.α不大于45°
B.0°<α<90°
C.α不大于90°
D.45°<α<90°
如图,MN是线段AB的垂直平分线,C在MN外,且与A点在MN的同一侧,BC交MN于P点,则(
)
A.BC>PC+AP
B.BC<PC+AP
C.BC=PC+AP
D.BC≥PC+AP
如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF的度数为(
)
A.48°
B.36°
C.30°
D.24°
如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于(
)
A.110°
B.120°
C.130°
D.140°
如图,已知下列三角形中,AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( )
A.①③④
B.①②③④
C.①②④
D.①③
、填空题
一个等腰三角形的一个角为80°,则它的顶角的度数是 .
已知一个等腰三角形两内角的度数之比为1:4,则这个等腰三角形顶角的度数为 .
若等腰三角形的一个外角为70°,则它的底角为
度.
已知等腰三角形的顶角为40°,则它一腰上的高与底边的夹角为
.
如图,在△ABC中,AB=AC,AD⊥BC于D点,点E、F分别是AD的三等分点,若△ABC的面积为18cm2,则图中阴影部分面积为
cm2.
如图,在Rt△ABC中,D,E为斜边AB上的两个点,且BD=BC,AE=AC,则∠DCE的大小
为
(度).
、解答题
如图,已知D、E两点在线段BC上,AB=AC,AD=AE.证明:BD=CE.
如图所示,已知在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E,若AB=5,求线段DE的长.
如图,△ABC中BD、CD平分∠ABC、∠ACB,过D作直线平行于BC,交AB、AC于E、F,求证:EF=BE+CF.
如图,在△ABC中,AB=AC,D、E分别在AC、AB边上,且BC=BD,AD=DE=EB,求∠A的度数.
如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(1)求证:BE=CE;
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其它条件不变.求证:△AEF≌△BCF.
参考答案
C
C
C
C
D
B
C
A
答案为:A.
A.
答案为:80°或20°.
答案为:120°或20°.
答案为:35.
答案为:20°.
答案为:9.
答案为:45.
证明:
过A作AF⊥BC于F,
∵AB=AC,AD=AE,AF⊥BC,
∴BF=CF,DF=EF,
∴BF﹣DF=CF﹣EF,
∴BD=CE.
解:在△ABC中,AB=AD=DC,
∵AB=AD,在三角形ABD中,
∠B=∠ADB=(180°﹣26°)×=77°,
又∵AD=DC,在三角形ADC中,
∴∠C==77°×=38.5°.
解:∵AD平分∠BAC,∴∠BAD=∠CAD,
∵DE∥AC,∴∠CAD=∠ADE,∴∠BAD=∠ADE,∴AE=DE,
∵AD⊥DB,∴∠ADB=90°,
∴∠EAD+∠ABD=90°,∠ADE+∠BDE=∠ADB=90°,
∴∠ABD=∠BDE,∴DE=BE,
∵AB=5,∴DE=BE=AE==2.5.
解:∵△ABC中BD、CD平分∠ABC、∠ACB,
∴∠1=∠2,∠5=∠6,
∵EF∥BC,∴∠2=∠3,∠4=∠6,
∴∠1=∠3,∠4=∠5,
根据在同一三角形中等角对等边的原则可知,BE=ED,DF=FC,
故EF=ED+DF=BE+CF.
解:∵DE=EB∴设∠BDE=∠ABD=x,
∴∠AED=∠BDE+∠ABD=2x,
∵AD=DE,∴∠AED=∠A=2x,
∴∠BDC=∠A+∠ABD=3x,
∵BD=BC,
∴∠C=∠BDC=3x,
∵AB=AC,
∴∠ABC=∠C=3x,
在△ABC中,3x+3x+2x=180°,解得x=22.5°,
∴∠A=2x=22.5°×2=45°.
证明:(1)∵AB=AC,D是BC的中点,
∴∠BAE=∠EAC,
在△ABE和△ACE中,,
∴△ABE≌△ACE(SAS),
∴BE=CE;
(2)∵∠BAC=45°,BF⊥AF,
∴△ABF为等腰直角三角形,
∴AF=BF,
∵AB=AC,点D是BC的中点,
∴AD⊥BC,
∴∠EAF+∠C=90°,
∵BF⊥AC,
∴∠CBF+∠C=90°,
∴∠EAF=∠CBF,
在△AEF和△BCF中,,
∴△AEF≌△BCF(ASA).
