苏科版八年级上册一次函数提优微专题:函数与特殊三角形、过定点、定直线问题、面积问题(word版,无答案)
文档属性
| 名称 | 苏科版八年级上册一次函数提优微专题:函数与特殊三角形、过定点、定直线问题、面积问题(word版,无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 765.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 21:19:18 | ||
图片预览



文档简介
微专题六:一次函数与动点构成特殊三角形
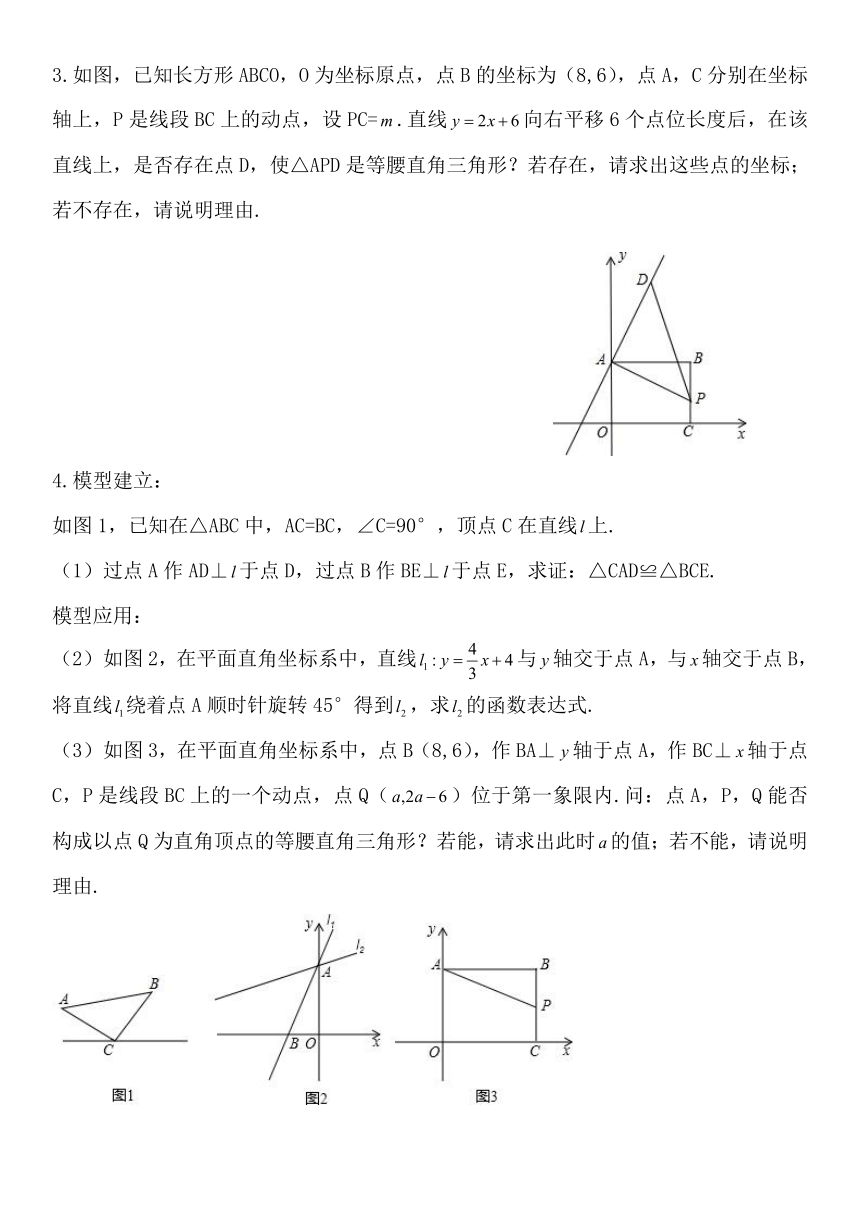
1.如图,直线与轴、轴分别交于两点,直线与轴、轴分别交于两点,点为直线的交点.
(1)试求出值及的面积;
(2)在轴上是否存在一点,使的面积与的面积相等.若存在,请求出点坐标;若不存在,请说明理由;
(3)点是轴上一动点,若是等腰三角形,
则点的坐标为
(写出所有可能的情况)
2.如图,直线与轴交于点C,与轴交于点A,过C、A分别作轴、轴的垂线交于点B,P是线段BC上的动点,(1)求A、C坐标;(2)若点Q位于第一象限内.问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请求出此时的值,若不能,请说明理由.
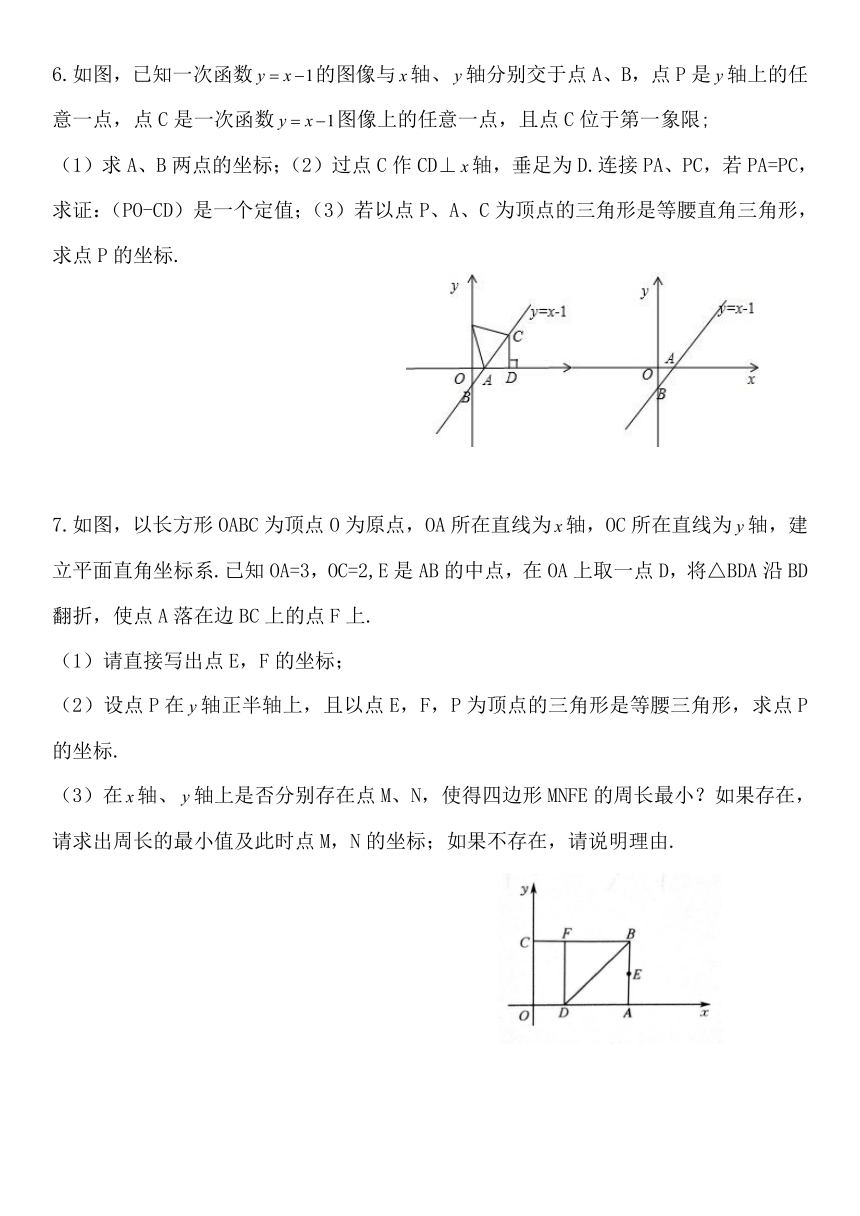
3.如图,已知长方形ABCO,O为坐标原点,点B的坐标为(8,6),点A,C分别在坐标轴上,P是线段BC上的动点,设PC=.直线向右平移6个点位长度后,在该直线上,是否存在点D,使△APD是等腰直角三角形?若存在,请求出这些点的坐标;若不存在,请说明理由.
4.模型建立:
如图1,已知在△ABC中,AC=BC,∠C=90°,顶点C在直线上.
(1)过点A作AD⊥于点D,过点B作BE⊥于点E,求证:△CAD≌△BCE.
模型应用:
如图2,在平面直角坐标系中,直线与轴交于点A,与轴交于点B,将直线绕着点A顺时针旋转45°得到,求的函数表达式.
如图3,在平面直角坐标系中,点B(8,6),作BA⊥轴于点A,作BC⊥轴于点C,P是线段BC上的一个动点,点Q()位于第一象限内.问:点A,P,Q能否构成以点Q为直角顶点的等腰直角三角形?若能,请求出此时的值;若不能,请说明理由.
5.如图,在平面直角坐标系中,一次函数的图象与轴的正半轴交于点,与轴交于点,的面积为2,动点从点出发,以每秒1个单位长度的速度在射线上运动,动点从出发,沿轴的正半轴与点同时以相同的速度运动,过作轴交直线于.
(1)求直线的解析式.
(2)当点在线段上运动时,设的面积为,点运动的时间为秒,求与的函数关系式(直接写出自变量的取值范围).
(3)过点作轴交直线于,在运动过程中(点不与点重合),是否存在某一时刻(秒),使是等腰三角形?若存在,求出时间的值.
6.如图,已知一次函数的图像与轴、轴分别交于点A、B,点P是轴上的任意一点,点C是一次函数图像上的任意一点,且点C位于第一象限;
(1)求A、B两点的坐标;(2)过点C作CD⊥轴,垂足为D.连接PA、PC,若PA=PC,求证:(PO-CD)是一个定值;(3)若以点P、A、C为顶点的三角形是等腰直角三角形,求点P的坐标.
7.如图,以长方形OABC为顶点O为原点,OA所在直线为轴,OC所在直线为轴,建立平面直角坐标系.已知OA=3,OC=2,E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在边BC上的点F上.
(1)请直接写出点E,F的坐标;
(2)设点P在轴正半轴上,且以点E,F,P为顶点的三角形是等腰三角形,求点P的坐标.
(3)在轴、轴上是否分别存在点M、N,使得四边形MNFE的周长最小?如果存在,请求出周长的最小值及此时点M,N的坐标;如果不存在,请说明理由.
微专题七:一次函数提升——过定点、定直线问题
1.关于直线:y=kx+k(k≠0),下列说法不正确的是(
)
A.点(0,k)在l上
B.经过定点(-1,0)
C.当k>0时,y随x的增大而增大
D.经过第一、二、三象限
2.无论取何值时,关于的一次函数必过一个定点,则这个定点的坐标为
.
3.已知点的坐标为,则点的纵坐标随横坐标变化的函数关系式可以
是
.
4.已知一次函数,且,则该一次函数图像必经过点
.
5.无论a取什么实数,点P
(a-1,2a-3)
都在直线l上.若Q
(m,n)
是直线l上的点,则
(2m-n+3)2的值等于
.
已知点P为平面直角坐标系中一点,其坐标是,则OP的最小值为
.
6.如图,直线与轴交于点C,与轴交于点A,过C、A分别作轴、轴的垂线交于点B,P是线段BC上的动点,(1)求A、C坐标;(2)若点Q位于第一象限内.问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请求出此时的值,若不能,请说明理由.
微专题八:一次函数与面积问题
1.如图,一次函数的图像与的图像交于点,且点的横坐标为,与轴、轴分别交于点、点.
(1)求的值与的长;
(2)若点为线段上一点,且,求点的坐标.
2.如图,已知直线:经过点,交轴于点,直线:与直线:交于点,交轴于点.
(1)求的值;
(2)求△BCD的面积.
(3)当时,则的取值范围是
;(直接写出结果)
3.如图,直线AD:y1=k1x+b1过点A(0,4),D(4,0),直线BC:y2=k2x+b2过点C(﹣2,0),且与直线AD交于点B,且点B的横坐标为a.
(1)当a=1时,求直线BC的解析式;
(2)在(1)的条件下,请直接写出k1x+b1>k2x+b2时,对应的x的取值范围;
(3)设△ABC的面积为S,用含a的代数式表示S,并求出当直线CB把△ACD的面积分为1:2的两部分时,对应a的值.
4.如图:直线y=kx+3与x轴、y轴分别交于A、B两点,,点C(x,y)是直线y=kx+3上与A、B不重合的动点.
(1)求直线y=kx+3的解析式;
(2)当点C运动到什么位置时△AOC的面积是6;
(3)过点C的另一直线CD与y轴相交于D点,是否存在点C使△BCD与△AOB全等?若存在,请求出点C的坐标;若不存在,请说明理由.
5.一次函数与的图像都经过点A,且与轴分别交于点B、C.
(1)试求△ABC的面积;
(2)过△ABC的顶点能否画一条直线,使它能平分△ABC的面积?若能,求出直线的函数关系式,若不能,说明理由.
6.如图,在平面直角坐标系中,一次函数的图像与轴、轴分别交于点,点的坐标为(2,0)
(1)求的值;
(2)已知点在第四象限,且到两坐标轴距离相等,若的面积是面积的2倍,
求点的坐标.
7.一次函数的图像与轴、轴分别交于点A、B.在轴左侧有一点P(-1,).
(1)如图,以线段AB为直角边在第一象限内作等腰直角三角形ABC,且∠BAC=90°,求点C的坐标.
(2)当时,求△ABP的面积.
(3)当时,点Q是直线上一点,且△POQ的面积为5,求点Q的坐标.
8.如图,一次函数的图像分别与轴、轴相交于点A,B,且与过点C(2,0)的一次函数的图像相交于点D,点D的横坐标为4,直线CD与轴相交于点E.
(1)直线CD的函数表达式为
.
(2)点Q为线段DE上的一个动点,连接EQ.
①若直线BQ将△BDE的面积分为1:2两部分,试求点Q的坐标.
②点
Q是否存在某个位置,将△BQD沿着直线BQ翻折,使得点D恰好落在直线AB下方的坐标轴上?若存在,求点Q的坐标;若不存在,请说明理由.
9.如图,在平面直角坐标系中,长方形的顶点的坐标分别为是的中点,动点从点出发,以每秒1个单位长度的速度,沿着运动,设点运动的时间为秒(0<<13).
(1)①点的坐标是(
,
);
②当点在上运动时,点的坐标是(
,
)
(用表示);
(2)写出的面积与之间的函数关系式,并求出的面积等于9时点的坐标;
(3)当点P在OA上运动时,连接BP,将线段BP绕点P逆时针旋转,点B恰好落到OC的中点处,则此时点运动的时间=
秒.(直接写出答案)
1.如图,直线与轴、轴分别交于两点,直线与轴、轴分别交于两点,点为直线的交点.
(1)试求出值及的面积;
(2)在轴上是否存在一点,使的面积与的面积相等.若存在,请求出点坐标;若不存在,请说明理由;
(3)点是轴上一动点,若是等腰三角形,
则点的坐标为
(写出所有可能的情况)
2.如图,直线与轴交于点C,与轴交于点A,过C、A分别作轴、轴的垂线交于点B,P是线段BC上的动点,(1)求A、C坐标;(2)若点Q位于第一象限内.问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请求出此时的值,若不能,请说明理由.
3.如图,已知长方形ABCO,O为坐标原点,点B的坐标为(8,6),点A,C分别在坐标轴上,P是线段BC上的动点,设PC=.直线向右平移6个点位长度后,在该直线上,是否存在点D,使△APD是等腰直角三角形?若存在,请求出这些点的坐标;若不存在,请说明理由.
4.模型建立:
如图1,已知在△ABC中,AC=BC,∠C=90°,顶点C在直线上.
(1)过点A作AD⊥于点D,过点B作BE⊥于点E,求证:△CAD≌△BCE.
模型应用:
如图2,在平面直角坐标系中,直线与轴交于点A,与轴交于点B,将直线绕着点A顺时针旋转45°得到,求的函数表达式.
如图3,在平面直角坐标系中,点B(8,6),作BA⊥轴于点A,作BC⊥轴于点C,P是线段BC上的一个动点,点Q()位于第一象限内.问:点A,P,Q能否构成以点Q为直角顶点的等腰直角三角形?若能,请求出此时的值;若不能,请说明理由.
5.如图,在平面直角坐标系中,一次函数的图象与轴的正半轴交于点,与轴交于点,的面积为2,动点从点出发,以每秒1个单位长度的速度在射线上运动,动点从出发,沿轴的正半轴与点同时以相同的速度运动,过作轴交直线于.
(1)求直线的解析式.
(2)当点在线段上运动时,设的面积为,点运动的时间为秒,求与的函数关系式(直接写出自变量的取值范围).
(3)过点作轴交直线于,在运动过程中(点不与点重合),是否存在某一时刻(秒),使是等腰三角形?若存在,求出时间的值.
6.如图,已知一次函数的图像与轴、轴分别交于点A、B,点P是轴上的任意一点,点C是一次函数图像上的任意一点,且点C位于第一象限;
(1)求A、B两点的坐标;(2)过点C作CD⊥轴,垂足为D.连接PA、PC,若PA=PC,求证:(PO-CD)是一个定值;(3)若以点P、A、C为顶点的三角形是等腰直角三角形,求点P的坐标.
7.如图,以长方形OABC为顶点O为原点,OA所在直线为轴,OC所在直线为轴,建立平面直角坐标系.已知OA=3,OC=2,E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在边BC上的点F上.
(1)请直接写出点E,F的坐标;
(2)设点P在轴正半轴上,且以点E,F,P为顶点的三角形是等腰三角形,求点P的坐标.
(3)在轴、轴上是否分别存在点M、N,使得四边形MNFE的周长最小?如果存在,请求出周长的最小值及此时点M,N的坐标;如果不存在,请说明理由.
微专题七:一次函数提升——过定点、定直线问题
1.关于直线:y=kx+k(k≠0),下列说法不正确的是(
)
A.点(0,k)在l上
B.经过定点(-1,0)
C.当k>0时,y随x的增大而增大
D.经过第一、二、三象限
2.无论取何值时,关于的一次函数必过一个定点,则这个定点的坐标为
.
3.已知点的坐标为,则点的纵坐标随横坐标变化的函数关系式可以
是
.
4.已知一次函数,且,则该一次函数图像必经过点
.
5.无论a取什么实数,点P
(a-1,2a-3)
都在直线l上.若Q
(m,n)
是直线l上的点,则
(2m-n+3)2的值等于
.
已知点P为平面直角坐标系中一点,其坐标是,则OP的最小值为
.
6.如图,直线与轴交于点C,与轴交于点A,过C、A分别作轴、轴的垂线交于点B,P是线段BC上的动点,(1)求A、C坐标;(2)若点Q位于第一象限内.问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请求出此时的值,若不能,请说明理由.
微专题八:一次函数与面积问题
1.如图,一次函数的图像与的图像交于点,且点的横坐标为,与轴、轴分别交于点、点.
(1)求的值与的长;
(2)若点为线段上一点,且,求点的坐标.
2.如图,已知直线:经过点,交轴于点,直线:与直线:交于点,交轴于点.
(1)求的值;
(2)求△BCD的面积.
(3)当时,则的取值范围是
;(直接写出结果)
3.如图,直线AD:y1=k1x+b1过点A(0,4),D(4,0),直线BC:y2=k2x+b2过点C(﹣2,0),且与直线AD交于点B,且点B的横坐标为a.
(1)当a=1时,求直线BC的解析式;
(2)在(1)的条件下,请直接写出k1x+b1>k2x+b2时,对应的x的取值范围;
(3)设△ABC的面积为S,用含a的代数式表示S,并求出当直线CB把△ACD的面积分为1:2的两部分时,对应a的值.
4.如图:直线y=kx+3与x轴、y轴分别交于A、B两点,,点C(x,y)是直线y=kx+3上与A、B不重合的动点.
(1)求直线y=kx+3的解析式;
(2)当点C运动到什么位置时△AOC的面积是6;
(3)过点C的另一直线CD与y轴相交于D点,是否存在点C使△BCD与△AOB全等?若存在,请求出点C的坐标;若不存在,请说明理由.
5.一次函数与的图像都经过点A,且与轴分别交于点B、C.
(1)试求△ABC的面积;
(2)过△ABC的顶点能否画一条直线,使它能平分△ABC的面积?若能,求出直线的函数关系式,若不能,说明理由.
6.如图,在平面直角坐标系中,一次函数的图像与轴、轴分别交于点,点的坐标为(2,0)
(1)求的值;
(2)已知点在第四象限,且到两坐标轴距离相等,若的面积是面积的2倍,
求点的坐标.
7.一次函数的图像与轴、轴分别交于点A、B.在轴左侧有一点P(-1,).
(1)如图,以线段AB为直角边在第一象限内作等腰直角三角形ABC,且∠BAC=90°,求点C的坐标.
(2)当时,求△ABP的面积.
(3)当时,点Q是直线上一点,且△POQ的面积为5,求点Q的坐标.
8.如图,一次函数的图像分别与轴、轴相交于点A,B,且与过点C(2,0)的一次函数的图像相交于点D,点D的横坐标为4,直线CD与轴相交于点E.
(1)直线CD的函数表达式为
.
(2)点Q为线段DE上的一个动点,连接EQ.
①若直线BQ将△BDE的面积分为1:2两部分,试求点Q的坐标.
②点
Q是否存在某个位置,将△BQD沿着直线BQ翻折,使得点D恰好落在直线AB下方的坐标轴上?若存在,求点Q的坐标;若不存在,请说明理由.
9.如图,在平面直角坐标系中,长方形的顶点的坐标分别为是的中点,动点从点出发,以每秒1个单位长度的速度,沿着运动,设点运动的时间为秒(0<<13).
(1)①点的坐标是(
,
);
②当点在上运动时,点的坐标是(
,
)
(用表示);
(2)写出的面积与之间的函数关系式,并求出的面积等于9时点的坐标;
(3)当点P在OA上运动时,连接BP,将线段BP绕点P逆时针旋转,点B恰好落到OC的中点处,则此时点运动的时间=
秒.(直接写出答案)
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
