3.6圆和圆的位置关系课件
图片预览




文档简介
(共15张PPT)
3.6、圆和圆的位置关系
课件改编:济宁十二中 陈伟利
教学目标:
经历探索两个圆之间位置关系的过程.
了解圆与圆之间的几种位置关系.
了解两圆外切、内切与两圆圆心距
d、半径R和r数量关系的联系.
在一张纸上作一个⊙O1,再在纸上任取一个不同于O1的点O2,以O2为圆心,以任意长为半径画一个⊙O2. 你画的⊙O2和⊙O1有公共点吗?有几个?你和同座位画的情形一样吗?想想看,以任意长为半径画⊙O2,⊙O1 和⊙O2会有几种不同的位置关系?你能把它们都画出来吗?
做一做
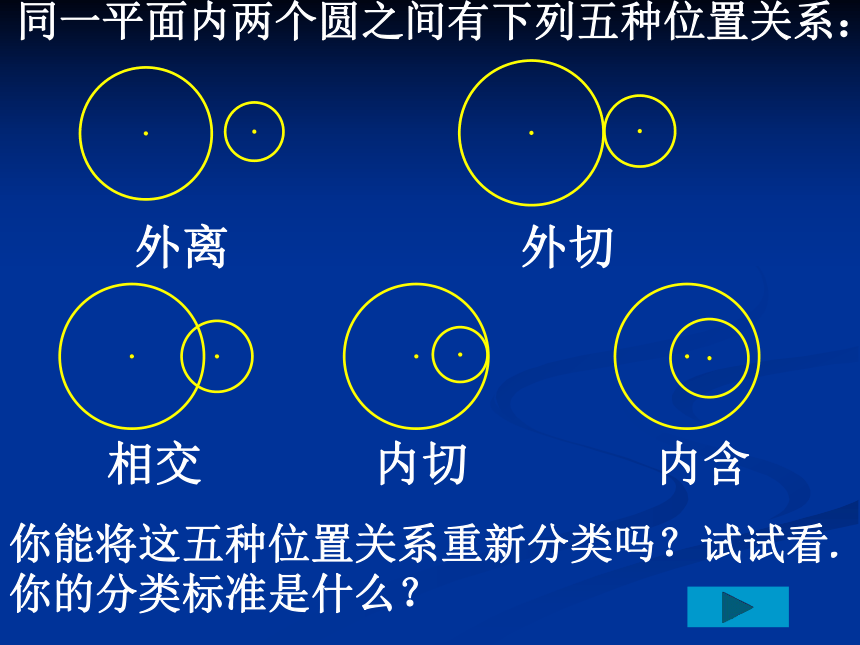
同一平面内两个圆之间有下列五种位置关系:
外离
外切
相交
内切
内含
你能将这五种位置关系重新分类吗?试试看.你的分类标准是什么?
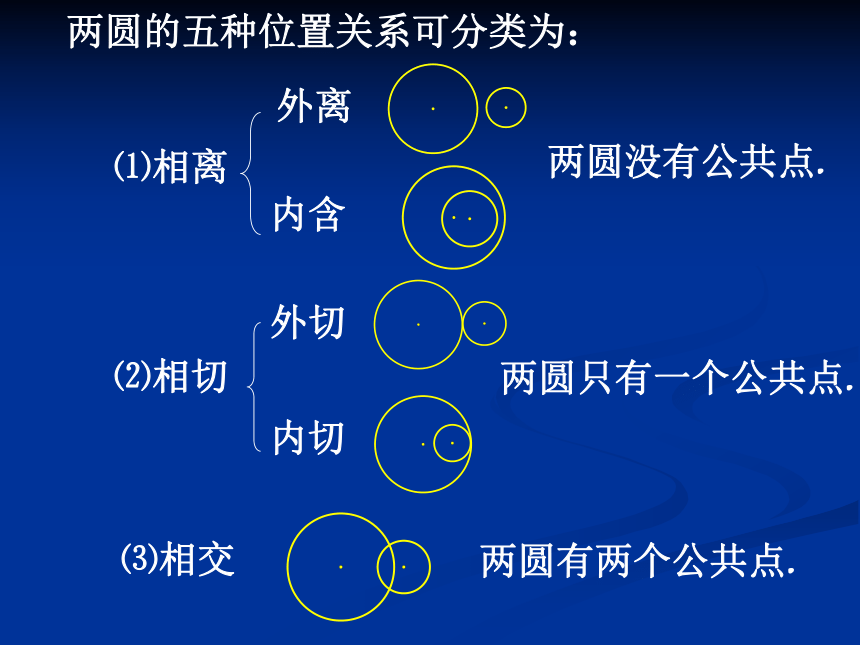
两圆的五种位置关系可分类为:
⑴相离
外离
内含
⑵相切
外切
内切
⑶相交
两圆没有公共点.
两圆只有一个公共点.
两圆有两个公共点.
想一想
下图是反映圆和圆位置关系的一些生活实例,你还能举出另外一些实例吗?
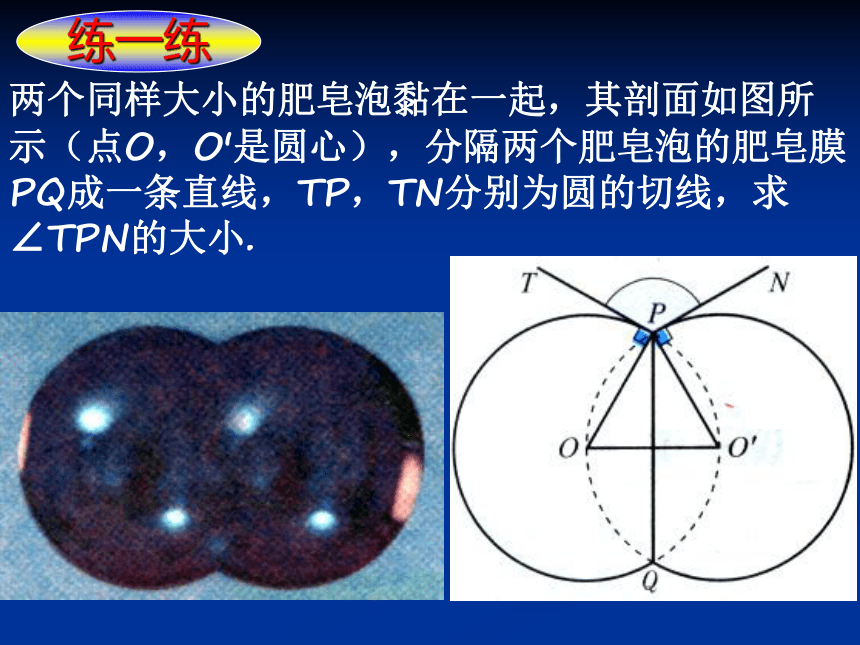
两个同样大小的肥皂泡黏在一起,其剖面如图所示(点O,O'是圆心),分隔两个肥皂泡的肥皂膜PQ成一条直线,TP,TN分别为圆的切线,求∠TPN的大小.
练一练
解:∵PO=OO'=PO',
∴△PO'O是一个等边三角形.
∴∠OPO'=60°,
又∵TP与NP分别为圆的切线,
∴TPO=90°, NPO=90 °.
∴TPN=360°-2×90°-60°=120°.
想一想
O1
O1
O2
O2
如图(1), ⊙O1 与⊙O2外切,这个图是轴对称图形吗?如果是,它的对称轴是什么?切点与对称轴有什么位置关系?如果 ⊙O1 与⊙O2内切呢?(如图(2) )
图(1)
图(2)
议一议
设两圆的半径分别为R和r
(1)当两圆外切时,两圆圆心之间的距离(简称圆心距)d与R和r具有怎样的关系?反之,当d与R和r满足这一关系时,这两个圆一定外切吗?
O1
O2
两圆外切
d=R+r
(2)当两圆内切时(R>r),圆心距d与R和r具有怎样的关系?反之,当d与R和r满足这一关系时,这两个圆一定内切吗?
O1
O2
两圆内切
d=R-r
问 题
⑴若两圆外切,圆心距是7cm,一个圆的半径是3cm,则另一个圆的半径是多少?
⑵若两圆相切,圆心距是7cm,一个圆的半径是3cm,则另一个圆的半径是多少?
⑶如图,已知⊙O1 ,半径为5cm,求作半径为2cm的⊙O2,使得⊙O2与 ⊙O1 相切.
O1
作业:
3.6、圆和圆的位置关系
课件改编:济宁十二中 陈伟利
教学目标:
经历探索两个圆之间位置关系的过程.
了解圆与圆之间的几种位置关系.
了解两圆外切、内切与两圆圆心距
d、半径R和r数量关系的联系.
在一张纸上作一个⊙O1,再在纸上任取一个不同于O1的点O2,以O2为圆心,以任意长为半径画一个⊙O2. 你画的⊙O2和⊙O1有公共点吗?有几个?你和同座位画的情形一样吗?想想看,以任意长为半径画⊙O2,⊙O1 和⊙O2会有几种不同的位置关系?你能把它们都画出来吗?
做一做
同一平面内两个圆之间有下列五种位置关系:
外离
外切
相交
内切
内含
你能将这五种位置关系重新分类吗?试试看.你的分类标准是什么?
两圆的五种位置关系可分类为:
⑴相离
外离
内含
⑵相切
外切
内切
⑶相交
两圆没有公共点.
两圆只有一个公共点.
两圆有两个公共点.
想一想
下图是反映圆和圆位置关系的一些生活实例,你还能举出另外一些实例吗?
两个同样大小的肥皂泡黏在一起,其剖面如图所示(点O,O'是圆心),分隔两个肥皂泡的肥皂膜PQ成一条直线,TP,TN分别为圆的切线,求∠TPN的大小.
练一练
解:∵PO=OO'=PO',
∴△PO'O是一个等边三角形.
∴∠OPO'=60°,
又∵TP与NP分别为圆的切线,
∴TPO=90°, NPO=90 °.
∴TPN=360°-2×90°-60°=120°.
想一想
O1
O1
O2
O2
如图(1), ⊙O1 与⊙O2外切,这个图是轴对称图形吗?如果是,它的对称轴是什么?切点与对称轴有什么位置关系?如果 ⊙O1 与⊙O2内切呢?(如图(2) )
图(1)
图(2)
议一议
设两圆的半径分别为R和r
(1)当两圆外切时,两圆圆心之间的距离(简称圆心距)d与R和r具有怎样的关系?反之,当d与R和r满足这一关系时,这两个圆一定外切吗?
O1
O2
两圆外切
d=R+r
(2)当两圆内切时(R>r),圆心距d与R和r具有怎样的关系?反之,当d与R和r满足这一关系时,这两个圆一定内切吗?
O1
O2
两圆内切
d=R-r
问 题
⑴若两圆外切,圆心距是7cm,一个圆的半径是3cm,则另一个圆的半径是多少?
⑵若两圆相切,圆心距是7cm,一个圆的半径是3cm,则另一个圆的半径是多少?
⑶如图,已知⊙O1 ,半径为5cm,求作半径为2cm的⊙O2,使得⊙O2与 ⊙O1 相切.
O1
作业:
