人教版八年级上册14.1.1同底数幂的乘法(共22张ppt)
文档属性
| 名称 | 人教版八年级上册14.1.1同底数幂的乘法(共22张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 229.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 22:20:20 | ||
图片预览







文档简介
第十四章 整式的乘法与因式分解
14.1 整式的乘法
14.1.1 同底数幂的乘法
八年级数学上(RJ)教学课件
疃里镇第三中学
学习目标
1.理解并掌握同底数幂的乘法法则.(重点)
2.能够运用同底数幂的乘法法则进行相关计算.(难点)
3.通过对同底数幂的乘法运算法则的推导与总结,提升自身的推理能力.
一、温故知新,引出法则
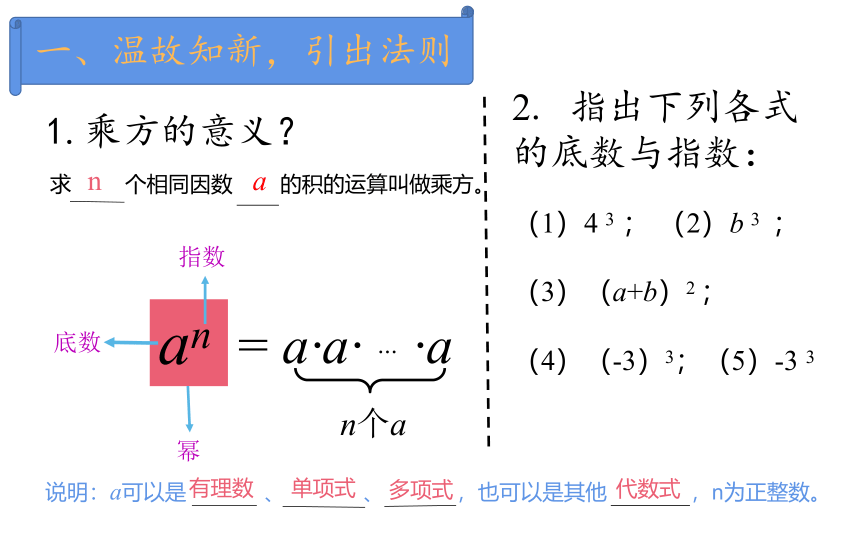
1.乘方的意义?
求 个相同因数 的积的运算叫做乘方。
n
a
an
= a·a· … ·a
n个a
指数
底数
幂
2. 指出下列各式的底数与指数:
(1)4 3 ; (2)b 3 ;
(3)(a+b)2 ;
(4)(-3)3;(5)-3 3
说明:a可以是 、 、 ,也可以是其他 ,n为正整数。
有理数
单项式
多项式
代数式
一、温故知新,引出法则
3.引例
神威·太湖之光超级计算机是世界上首台每秒运算速度超过十亿亿次(1017)的超级计算机.它工作103s可进行多少次运算?
问题1 怎样列式?
1017 ×103
问题2 怎样计算?
二、归纳概括,探究法则
1.初探法则:
(1) 102×103 ; (2) 105×108; (3) 10m×10n (m, n都是正整数)
问题1 根据乘方的意义,尝试计算102×103.
102×103=
×(10×10×10)
(10×10)
5个10
= 10 2+3
二、归纳概括,探究法则
类似地可以得出:
(2) 105×108 =1013=105+8
(3) 10m×10n =10 m+n
问题2 乘法算式中两个幂因数有何特点?
把底数换成其他数试一试:
(4) 2m×2n =
(5) (-3)m×(-3)n =
(6) a2×a3 =a 2+3=
2m+n
(-3)m+n
a5
两个幂的底数相同,称为同底数幂。
问题3 结果和算式中两个幂有什么关系?
底数和前面相同,指数则是左边两个指数的和。
二、归纳概括,探究法则
2.建立法则:
猜想:
am×an = a( ),m, n都是正整数.
m+n
你能利用乘方的意义推导吗?
am×an=
( 个a)
(a·a·…a)
m
(a·a·…a)
·
n
( 个a)
=a( )
m+n
同底数幂的乘法法则
同底数幂相乘,底数不变,指数相加
3.剖析法则:
(1)等号左边是什么运算?
同底数幂相乘
(2)等号两边的底数有什么关系?
相同,即“底数不变”
(3)等号两边的指数有什么关系?
右边指数是左边两个指数的和
(4)公式中的底数a可以表示什么?
有理数,单项式,多项式或者其他代数式
三、应用举例,巩固法则
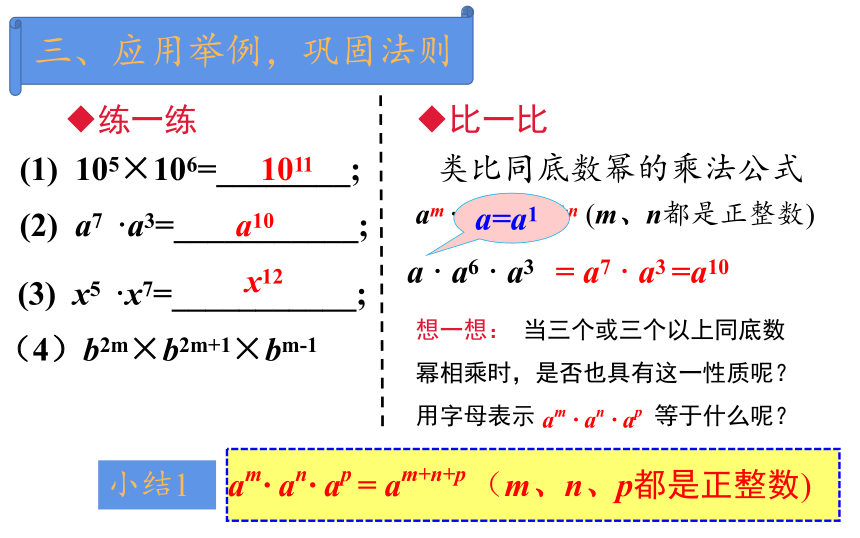
(1) 105×106=________;
1011
(2) a7 ·a3=___________;
a10
(3) x5 ·x7=___________;
x12
练一练
比一比
类比同底数幂的乘法公式
am · an = am+n (m、n都是正整数)
a · a6 · a3
= a7 · a3 =a10
想一想: 当三个或三个以上同底数幂相乘时,是否也具有这一性质呢?用字母表示 等于什么呢?
am · an · ap
am· an· ap = am+n+p (m、n、p都是正整数)
小结1
a=a1
(4)b2m×b2m+1×bm-1
三、应用举例,巩固法则
练一练
7
3
×
(1)(-3)7×(-3)6
(2) 1
7
1
2
(3)-x3×x5
解:
(1)(-3)7×(-3)6 =(-3)7+6=(-3)13
3+2
1
7
2
3
×
(2) =
1
7
1
7
1
7
=
5
(3) -x3×x5=-x3+5 =-x8
小结2
正确运用同底数幂乘法法则可概括为“一看、二定、三计算”
“一 看”:看底数是否相同(或可化为相同),看是否是两个(或多个)幂相乘.
“二 定”:确定采用“同底数幂乘法法则”.
“三计算”:底数不变,指数相加,得出结果.
(4) b3 ×(-b)2
(4) b3 ×(-b)2=b3×b2=b3+2=b5
三、应用举例,巩固法则
例1 计算:
(1)x2 ·(- x)5 ;
(2)a · (-a)6;
(3)(-2) × (-2)4 × (-2)3;
(4) xm · x3m+1.
解:(1) x2 · (-x)5= -x2·x5= - x2+5 =-x7
(2)a ·(- a)6= a1+6 = a7;
(3)(-2) × (-2)4 × (-2)3= (-2) 1+4+3 = (-2)8 = 256;
(4) xm · x3m+1= xm+3m+1 = x4m+1.
解析:当两个幂的底数为相反数时,变形后可以运用同底数幂的乘法法则。
三、应用举例,巩固法则
例2 计算:
(1)(a+b)4 · (a+b)7 ;
(2)(m-n)3 ·(m-n)5 ·(m-n)7 ;
(3)(x-y)2·(y-x)5.
解析:当两个幂的底数为多项式时,把多项式看作一个整体仍可以运用同底数幂的乘法法则。
解:(1) (a+b)4 · (a+b)7 = (a+b)4+7 =(a+b)11;
(2)(m-n)3 ·(m-n)5 ·(m-n)7 =(m-n)3+5+7=(m-n)15;
(3)(x-y)2·(y-x)5=(y-x)2(y-x)5
=(y-x)2+5=(y-x)7.
三、应用举例,巩固法则
小结3
底数不同先转换,底数相同再运算.转换时常用到以下变形:
n为偶数
n为奇数
(-a)n=
-an.
an,
n为偶数
n为奇数
跟踪联系:
(1) -a4·(-a)2=_______;
-a6
(2) (a-b)2·(a-b)3=_______;
(a-b)5
三、应用举例,巩固法则
想一想:am+n可以写成哪两个因式的积?
am+n = am · an
填一填:若xm =3 ,xn =2,那么,
(1)xm+n = × = × = ;
xm
xn
3
2
6
(2)x2m = × = × = ;
xm
xm
3
9
3
同底数幂乘法法则的逆用
(1)将所求代数式转化为几个已知因式的乘积的形式,然后再求值.
(2)将等式两边转化为底数相同的形式,然后根据指数相等列方程解答.
小结4
下面的计算对不对?如果不对,应当怎样改正.
(1)b3·b3=2b3 (2)b3+b3=b6
(3)a·a5·a3=a8 (4)(-x)4·(-x)4=(-x)16
×
×
×
×
b6
2b3
=x8
a9
(-x)8
练一练:
注意区分同底数幂乘法和合并同类项:
(1)同类项要求各项每个幂因数的底数和指数均相同,合并后各幂的底数和指数不变。
(2)同底数幂乘法只要求底数相同,指数可以不同。
小结5
三、应用举例,巩固法则
四、明辨是非,深化法则
1.引例解答
神威·太湖之光超级计算机是世界上首台每秒运算速度超过十亿亿次(1017次)的超级计算机.它工作103s可进行多少次运算?
问题1 怎样列式?
1017 ×103
问题2 怎样计算?
1017×103
=(10×10×10 ×…×10)
17个10
×(10×10×10)
3个10
=10×10×…×10
20个10
=1020
=1017+3
四、明辨是非,深化法则
问题2 怎样计算?
解:
1.下列各式的结果等于26的是( )
A 2+25 B 2·25
C 23·25 D 0.22· 0.24
B
2.下列计算结果正确的是( )
A a3 · a3=a9 B m2 · n2=mn4
C xm · x3=x3m D y · yn=yn+1
D
四、明辨是非,深化法则
(1)x·x2·x( )=x7; (2)xm·( )=x3m;
(3)8×4=2x,则x=( ).
4
5
x2m
4.填空:
3.计算:
(1) xn+1·x2n=_______;
(2) (a-b)2·(a-b)3=_______;
(3) -a4·(-a)2=_______;
(4) y4·y3·y2·y =_______.
x3n+1
(a-b)5
-a6
y10
四、明辨是非,深化法则
5.计算下列各题:
(4)-a3·(-a)2·(-a)3.
(2)(a-b)3·(b-a)4;
(3) (-3)×(-3)2 ×(-3)3;
(1)(2a+b)2n+1·(2a+b)3;
解:(1)(2a+b)2n+1·(2a+b)3=(2a+b)2n+4;
(2)(a-b)3·(b-a)4=(a-b)7;
(3) (-3)×(-3)2 ×(-3)3=36;
(4)-a3·(-a)2·(-a)3=a8.
四、明辨是非,深化法则
(2)已知an-3·a2n+1=a10, 求n的值;
解:n-3+2n+1=10,
n=4;
6.(1)已知xa=8, xb=9, 求xa+b的值;
解:xa+b=xa·xb
=8×9=72;
(3) 3×27×9 = 32x-4, 求x的值;
解:3×27×9 =3×33×32=32x-4,
2x-4=6;
x=5.
四、明辨是非,深化法则
同底数幂的乘法
法则
am·an=am+n (m,n都是正整数)
注意
同底数幂相乘,底数不变,指数相加
am·an·ap=am+n+p(m,n,p都是正整数)
直接应用法则
常见变形:(-a)2=a2, (-a)3=-a3
底数相同时
底数不相同时
先变成同底数再应用法则
五、课堂小结
六、课后作业
1、课本:104页 复习巩固第1题
2、智慧学习:88页
14.1 整式的乘法
14.1.1 同底数幂的乘法
八年级数学上(RJ)教学课件
疃里镇第三中学
学习目标
1.理解并掌握同底数幂的乘法法则.(重点)
2.能够运用同底数幂的乘法法则进行相关计算.(难点)
3.通过对同底数幂的乘法运算法则的推导与总结,提升自身的推理能力.
一、温故知新,引出法则
1.乘方的意义?
求 个相同因数 的积的运算叫做乘方。
n
a
an
= a·a· … ·a
n个a
指数
底数
幂
2. 指出下列各式的底数与指数:
(1)4 3 ; (2)b 3 ;
(3)(a+b)2 ;
(4)(-3)3;(5)-3 3
说明:a可以是 、 、 ,也可以是其他 ,n为正整数。
有理数
单项式
多项式
代数式
一、温故知新,引出法则
3.引例
神威·太湖之光超级计算机是世界上首台每秒运算速度超过十亿亿次(1017)的超级计算机.它工作103s可进行多少次运算?
问题1 怎样列式?
1017 ×103
问题2 怎样计算?
二、归纳概括,探究法则
1.初探法则:
(1) 102×103 ; (2) 105×108; (3) 10m×10n (m, n都是正整数)
问题1 根据乘方的意义,尝试计算102×103.
102×103=
×(10×10×10)
(10×10)
5个10
= 10 2+3
二、归纳概括,探究法则
类似地可以得出:
(2) 105×108 =1013=105+8
(3) 10m×10n =10 m+n
问题2 乘法算式中两个幂因数有何特点?
把底数换成其他数试一试:
(4) 2m×2n =
(5) (-3)m×(-3)n =
(6) a2×a3 =a 2+3=
2m+n
(-3)m+n
a5
两个幂的底数相同,称为同底数幂。
问题3 结果和算式中两个幂有什么关系?
底数和前面相同,指数则是左边两个指数的和。
二、归纳概括,探究法则
2.建立法则:
猜想:
am×an = a( ),m, n都是正整数.
m+n
你能利用乘方的意义推导吗?
am×an=
( 个a)
(a·a·…a)
m
(a·a·…a)
·
n
( 个a)
=a( )
m+n
同底数幂的乘法法则
同底数幂相乘,底数不变,指数相加
3.剖析法则:
(1)等号左边是什么运算?
同底数幂相乘
(2)等号两边的底数有什么关系?
相同,即“底数不变”
(3)等号两边的指数有什么关系?
右边指数是左边两个指数的和
(4)公式中的底数a可以表示什么?
有理数,单项式,多项式或者其他代数式
三、应用举例,巩固法则
(1) 105×106=________;
1011
(2) a7 ·a3=___________;
a10
(3) x5 ·x7=___________;
x12
练一练
比一比
类比同底数幂的乘法公式
am · an = am+n (m、n都是正整数)
a · a6 · a3
= a7 · a3 =a10
想一想: 当三个或三个以上同底数幂相乘时,是否也具有这一性质呢?用字母表示 等于什么呢?
am · an · ap
am· an· ap = am+n+p (m、n、p都是正整数)
小结1
a=a1
(4)b2m×b2m+1×bm-1
三、应用举例,巩固法则
练一练
7
3
×
(1)(-3)7×(-3)6
(2) 1
7
1
2
(3)-x3×x5
解:
(1)(-3)7×(-3)6 =(-3)7+6=(-3)13
3+2
1
7
2
3
×
(2) =
1
7
1
7
1
7
=
5
(3) -x3×x5=-x3+5 =-x8
小结2
正确运用同底数幂乘法法则可概括为“一看、二定、三计算”
“一 看”:看底数是否相同(或可化为相同),看是否是两个(或多个)幂相乘.
“二 定”:确定采用“同底数幂乘法法则”.
“三计算”:底数不变,指数相加,得出结果.
(4) b3 ×(-b)2
(4) b3 ×(-b)2=b3×b2=b3+2=b5
三、应用举例,巩固法则
例1 计算:
(1)x2 ·(- x)5 ;
(2)a · (-a)6;
(3)(-2) × (-2)4 × (-2)3;
(4) xm · x3m+1.
解:(1) x2 · (-x)5= -x2·x5= - x2+5 =-x7
(2)a ·(- a)6= a1+6 = a7;
(3)(-2) × (-2)4 × (-2)3= (-2) 1+4+3 = (-2)8 = 256;
(4) xm · x3m+1= xm+3m+1 = x4m+1.
解析:当两个幂的底数为相反数时,变形后可以运用同底数幂的乘法法则。
三、应用举例,巩固法则
例2 计算:
(1)(a+b)4 · (a+b)7 ;
(2)(m-n)3 ·(m-n)5 ·(m-n)7 ;
(3)(x-y)2·(y-x)5.
解析:当两个幂的底数为多项式时,把多项式看作一个整体仍可以运用同底数幂的乘法法则。
解:(1) (a+b)4 · (a+b)7 = (a+b)4+7 =(a+b)11;
(2)(m-n)3 ·(m-n)5 ·(m-n)7 =(m-n)3+5+7=(m-n)15;
(3)(x-y)2·(y-x)5=(y-x)2(y-x)5
=(y-x)2+5=(y-x)7.
三、应用举例,巩固法则
小结3
底数不同先转换,底数相同再运算.转换时常用到以下变形:
n为偶数
n为奇数
(-a)n=
-an.
an,
n为偶数
n为奇数
跟踪联系:
(1) -a4·(-a)2=_______;
-a6
(2) (a-b)2·(a-b)3=_______;
(a-b)5
三、应用举例,巩固法则
想一想:am+n可以写成哪两个因式的积?
am+n = am · an
填一填:若xm =3 ,xn =2,那么,
(1)xm+n = × = × = ;
xm
xn
3
2
6
(2)x2m = × = × = ;
xm
xm
3
9
3
同底数幂乘法法则的逆用
(1)将所求代数式转化为几个已知因式的乘积的形式,然后再求值.
(2)将等式两边转化为底数相同的形式,然后根据指数相等列方程解答.
小结4
下面的计算对不对?如果不对,应当怎样改正.
(1)b3·b3=2b3 (2)b3+b3=b6
(3)a·a5·a3=a8 (4)(-x)4·(-x)4=(-x)16
×
×
×
×
b6
2b3
=x8
a9
(-x)8
练一练:
注意区分同底数幂乘法和合并同类项:
(1)同类项要求各项每个幂因数的底数和指数均相同,合并后各幂的底数和指数不变。
(2)同底数幂乘法只要求底数相同,指数可以不同。
小结5
三、应用举例,巩固法则
四、明辨是非,深化法则
1.引例解答
神威·太湖之光超级计算机是世界上首台每秒运算速度超过十亿亿次(1017次)的超级计算机.它工作103s可进行多少次运算?
问题1 怎样列式?
1017 ×103
问题2 怎样计算?
1017×103
=(10×10×10 ×…×10)
17个10
×(10×10×10)
3个10
=10×10×…×10
20个10
=1020
=1017+3
四、明辨是非,深化法则
问题2 怎样计算?
解:
1.下列各式的结果等于26的是( )
A 2+25 B 2·25
C 23·25 D 0.22· 0.24
B
2.下列计算结果正确的是( )
A a3 · a3=a9 B m2 · n2=mn4
C xm · x3=x3m D y · yn=yn+1
D
四、明辨是非,深化法则
(1)x·x2·x( )=x7; (2)xm·( )=x3m;
(3)8×4=2x,则x=( ).
4
5
x2m
4.填空:
3.计算:
(1) xn+1·x2n=_______;
(2) (a-b)2·(a-b)3=_______;
(3) -a4·(-a)2=_______;
(4) y4·y3·y2·y =_______.
x3n+1
(a-b)5
-a6
y10
四、明辨是非,深化法则
5.计算下列各题:
(4)-a3·(-a)2·(-a)3.
(2)(a-b)3·(b-a)4;
(3) (-3)×(-3)2 ×(-3)3;
(1)(2a+b)2n+1·(2a+b)3;
解:(1)(2a+b)2n+1·(2a+b)3=(2a+b)2n+4;
(2)(a-b)3·(b-a)4=(a-b)7;
(3) (-3)×(-3)2 ×(-3)3=36;
(4)-a3·(-a)2·(-a)3=a8.
四、明辨是非,深化法则
(2)已知an-3·a2n+1=a10, 求n的值;
解:n-3+2n+1=10,
n=4;
6.(1)已知xa=8, xb=9, 求xa+b的值;
解:xa+b=xa·xb
=8×9=72;
(3) 3×27×9 = 32x-4, 求x的值;
解:3×27×9 =3×33×32=32x-4,
2x-4=6;
x=5.
四、明辨是非,深化法则
同底数幂的乘法
法则
am·an=am+n (m,n都是正整数)
注意
同底数幂相乘,底数不变,指数相加
am·an·ap=am+n+p(m,n,p都是正整数)
直接应用法则
常见变形:(-a)2=a2, (-a)3=-a3
底数相同时
底数不相同时
先变成同底数再应用法则
五、课堂小结
六、课后作业
1、课本:104页 复习巩固第1题
2、智慧学习:88页
