人教版八年级上册14.3.2公式法——平方差公式课件(共20张ppt)
文档属性
| 名称 | 人教版八年级上册14.3.2公式法——平方差公式课件(共20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 847.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 22:23:30 | ||
图片预览







文档简介
人教版八年级上册
14.3.2公式法——平方差公式
2、判断下列变形过程,哪些是因式分解?
(1) (x+2)(x-2)=x2- 4 ( )
(2) x2- 4+3x=(x+2)(x-2)+3x ( )
(3) 7m-7n-7=7(m-n-1) ( )
(4) 4x2- 9 =(2x+3)(2x- 3 ) ( )
×
×
√
√
1:什么叫多项式的因式分解?
把一个多项式化为几个整式乘积的形式,叫做多项式的因式分解
复习回顾:
你们能快速计算:
752- 252 =?吗?
情景设置
1、什么叫分解因式?
把一个多项式化成几个整式的积的形式,叫做多项式的分解因式.
一、激趣导入—复习旧知
2、已学过哪一种分解因式的方法?
提公因式法
3、【问题】你能将a2-b2分解因式吗?
你是如何思考的?
学习目标:
1、探索能用平方差公式进行因式分解的多项式特征。
2、正确熟练运用平方差公式进行分解因式。
两个数的平 方差,等于这两个数的和与这两个数的差的积.
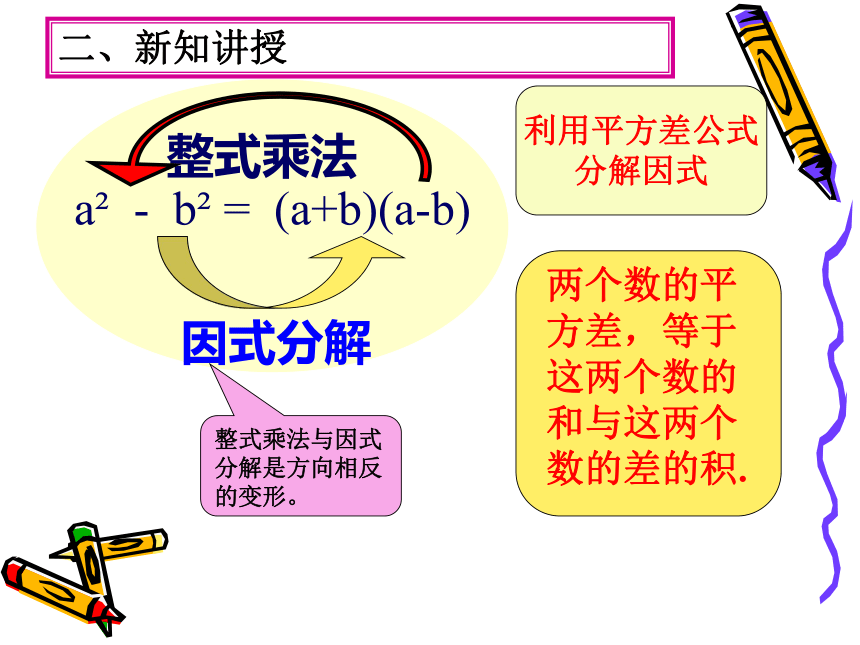
a? - b? = (a+b)(a-b)
因式分解
整式乘法
整式乘法与因式分解是方向相反的变形。
利用平方差公式
分解因式
二、新知讲授
思考:多项式 a2-b2 有什么特点?你能将它分解因式吗?
(a+b)(a-b)=a2 - b2
a2 - b2 =(a+b)(a-b)
等号两边
互换位置
特点:(1)多项式是一个二项式;
(2)有两个平方项,且两项的符号相反。
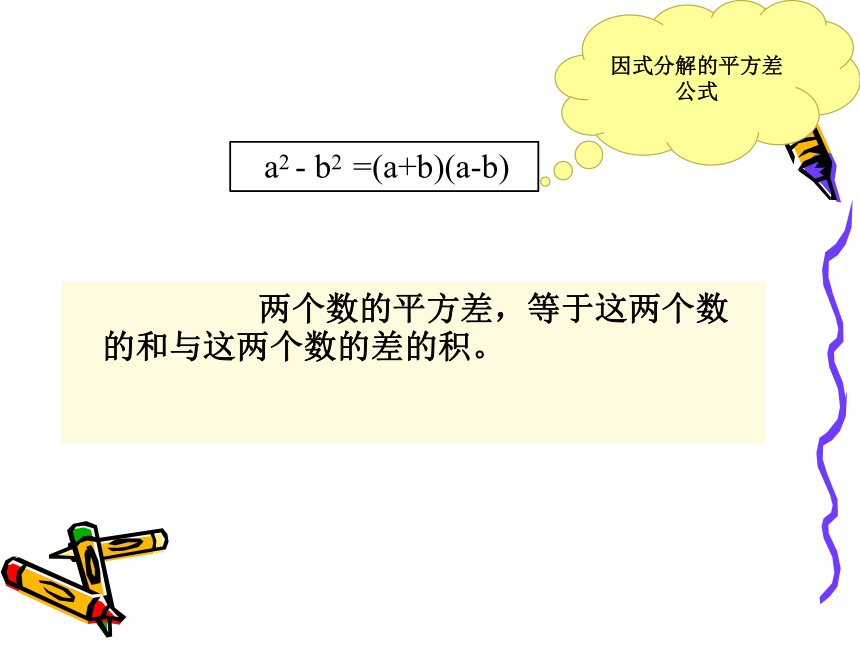
两个数的平方差,等于这两个数的和与这两个数的差的积。
a2 - b2 =(a+b)(a-b)
因式分解的平方差公式
下列多项式能否用平方差公式分解因式?为什么?
(1) ; (2) ;
(3) ; (4) .
不能。
因为两个平方项符号相同,不符合条件。
能。
该多项式是两个数的平方差的形式。
三、应用新知
能。
该多项式是两个数的平方差的形式。
不能。
因为两个平方项符号相同,不符合条件。
例1.分解因式
(1) 4x? - 9 (2 ) (x+p)? - (x+q)?
4x? - 9= (2x)? - 3?
a? - b? = ( a + b)( a - b )
(x+p)?-(x+q)?
= ( 2x + 3 )(2x - 3)
=[(x+p)+(x+q)][(x+p) -(x+q)]
=(2x+p+q)(p-q)
三、应用新知
三、应用新知
例1 分解因式:
(1) (2) .
解:(2)
练习1 将下列多项式分解因式:
(1) (2)
三、应用新知
三、应用新知
例2 分解因式:
(1) (2) .
解:(1)
三、应用新知
例2 分解因式:
(1) (2) .
解:(1)
练习2 将下列多项式分解因式:
(1) (2)
解:原式= y ( x2 - 4 )
= y ( x2 - 22 )
= y (x + 2 )( x – 2 )
解:原式 = 16 – a4
= 42 - (a2) 2
= (4+ a2)(4- a2)
= (4+ a2)(2+ a)(2-a)
三、应用新知
(1)9a2-4b2;
(2)x2y-4y;
(3)(a+1)2-1;
(4)x4-1;
(5)(x+y+z)2-(x-y+z)2.
四、实练:应用平方进行分解因式
(1)1002-992
(2)682-672
(4) 5.52-4.52
8
15
(
)
2
7
15
(
)
2
-
(3)
看谁算的又快又准确!
比一比!
等号两边
互换位置
整式乘法
因式分解
a、b可表示单项式,多项式等
公式结构特点
(1)多项式是一个二项式,有两个平方项,且两项的符号相反;
(2)等号右边是两个数的和与这两个数的差的积。
整体思想
1、提公因式
2、判断能否用平方差公式分解
3、检查分解是否彻底
a2 - b2 = (a+b)(a-b)
(a+b)(a-b) =a2 -b2
五、课堂小结
两个数的平方差,等于这两个数的和与这两个数的差的积。
文字语言表述
谢谢聆听
14.3.2公式法——平方差公式
2、判断下列变形过程,哪些是因式分解?
(1) (x+2)(x-2)=x2- 4 ( )
(2) x2- 4+3x=(x+2)(x-2)+3x ( )
(3) 7m-7n-7=7(m-n-1) ( )
(4) 4x2- 9 =(2x+3)(2x- 3 ) ( )
×
×
√
√
1:什么叫多项式的因式分解?
把一个多项式化为几个整式乘积的形式,叫做多项式的因式分解
复习回顾:
你们能快速计算:
752- 252 =?吗?
情景设置
1、什么叫分解因式?
把一个多项式化成几个整式的积的形式,叫做多项式的分解因式.
一、激趣导入—复习旧知
2、已学过哪一种分解因式的方法?
提公因式法
3、【问题】你能将a2-b2分解因式吗?
你是如何思考的?
学习目标:
1、探索能用平方差公式进行因式分解的多项式特征。
2、正确熟练运用平方差公式进行分解因式。
两个数的平 方差,等于这两个数的和与这两个数的差的积.
a? - b? = (a+b)(a-b)
因式分解
整式乘法
整式乘法与因式分解是方向相反的变形。
利用平方差公式
分解因式
二、新知讲授
思考:多项式 a2-b2 有什么特点?你能将它分解因式吗?
(a+b)(a-b)=a2 - b2
a2 - b2 =(a+b)(a-b)
等号两边
互换位置
特点:(1)多项式是一个二项式;
(2)有两个平方项,且两项的符号相反。
两个数的平方差,等于这两个数的和与这两个数的差的积。
a2 - b2 =(a+b)(a-b)
因式分解的平方差公式
下列多项式能否用平方差公式分解因式?为什么?
(1) ; (2) ;
(3) ; (4) .
不能。
因为两个平方项符号相同,不符合条件。
能。
该多项式是两个数的平方差的形式。
三、应用新知
能。
该多项式是两个数的平方差的形式。
不能。
因为两个平方项符号相同,不符合条件。
例1.分解因式
(1) 4x? - 9 (2 ) (x+p)? - (x+q)?
4x? - 9= (2x)? - 3?
a? - b? = ( a + b)( a - b )
(x+p)?-(x+q)?
= ( 2x + 3 )(2x - 3)
=[(x+p)+(x+q)][(x+p) -(x+q)]
=(2x+p+q)(p-q)
三、应用新知
三、应用新知
例1 分解因式:
(1) (2) .
解:(2)
练习1 将下列多项式分解因式:
(1) (2)
三、应用新知
三、应用新知
例2 分解因式:
(1) (2) .
解:(1)
三、应用新知
例2 分解因式:
(1) (2) .
解:(1)
练习2 将下列多项式分解因式:
(1) (2)
解:原式= y ( x2 - 4 )
= y ( x2 - 22 )
= y (x + 2 )( x – 2 )
解:原式 = 16 – a4
= 42 - (a2) 2
= (4+ a2)(4- a2)
= (4+ a2)(2+ a)(2-a)
三、应用新知
(1)9a2-4b2;
(2)x2y-4y;
(3)(a+1)2-1;
(4)x4-1;
(5)(x+y+z)2-(x-y+z)2.
四、实练:应用平方进行分解因式
(1)1002-992
(2)682-672
(4) 5.52-4.52
8
15
(
)
2
7
15
(
)
2
-
(3)
看谁算的又快又准确!
比一比!
等号两边
互换位置
整式乘法
因式分解
a、b可表示单项式,多项式等
公式结构特点
(1)多项式是一个二项式,有两个平方项,且两项的符号相反;
(2)等号右边是两个数的和与这两个数的差的积。
整体思想
1、提公因式
2、判断能否用平方差公式分解
3、检查分解是否彻底
a2 - b2 = (a+b)(a-b)
(a+b)(a-b) =a2 -b2
五、课堂小结
两个数的平方差,等于这两个数的和与这两个数的差的积。
文字语言表述
谢谢聆听
