人教版八年级上册数学课件:13.1.2.1线段的垂直平分线的性质(共22张ppt)
文档属性
| 名称 | 人教版八年级上册数学课件:13.1.2.1线段的垂直平分线的性质(共22张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 579.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览




文档简介
13.1.2 线段的垂直平
分线的性质(1)
一、教学目标?
1、?能够利用尺规作已知线段的垂直平分线;?
2、?能已知底边及底边上的高用尺规作等腰三角形?
二、教学重、难点?、
1、重点:用尺规作已知线段垂直平分线?
2、难点:已知底边及底边上的高求作等腰三角形?
三、教学过程
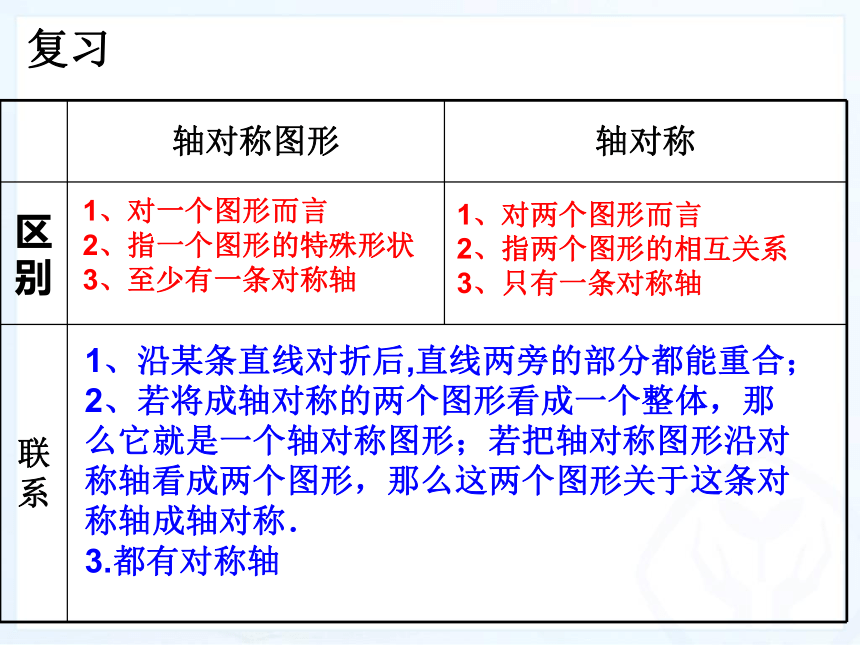
轴对称图形
轴对称
区别
联系
1、对两个图形而言
2、指两个图形的相互关系
3、只有一条对称轴
1、对一个图形而言
2、指一个图形的特殊形状
3、至少有一条对称轴
1、沿某条直线对折后,直线两旁的部分都能重合;
2、若将成轴对称的两个图形看成一个整体,那么它就是一个轴对称图形;若把轴对称图形沿对称轴看成两个图形,那么这两个图形关于这条对称轴成轴对称.
3.都有对称轴
复习
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线
轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线
你能用不同的方法验证
这一结论吗?
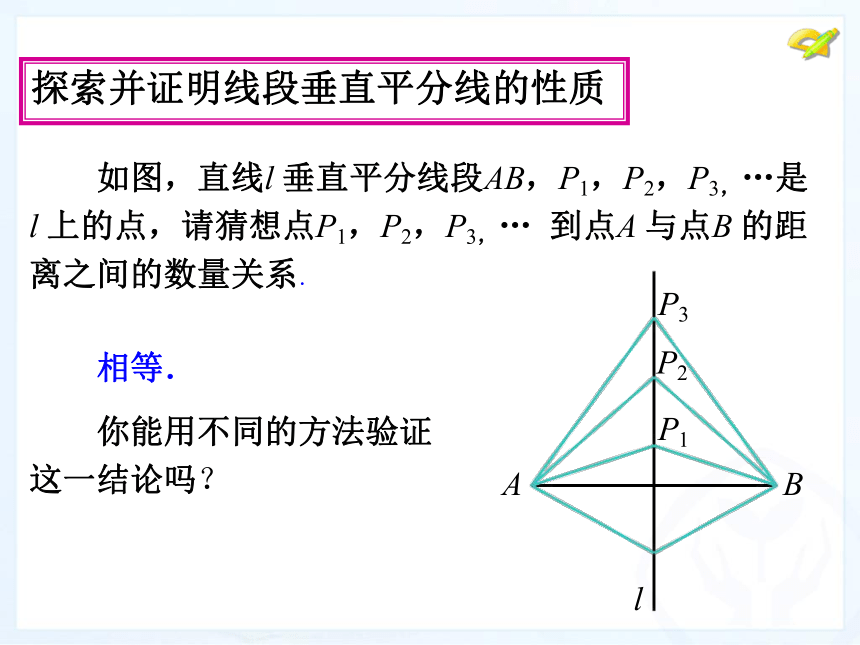
探索并证明线段垂直平分线的性质
如图,直线l 垂直平分线段AB,P1,P2,P3,…是
l 上的点,请猜想点P1,P2,P3,… 到点A 与点B 的距
离之间的数量关系.
相等.
A
B
l
P1
P2
P3
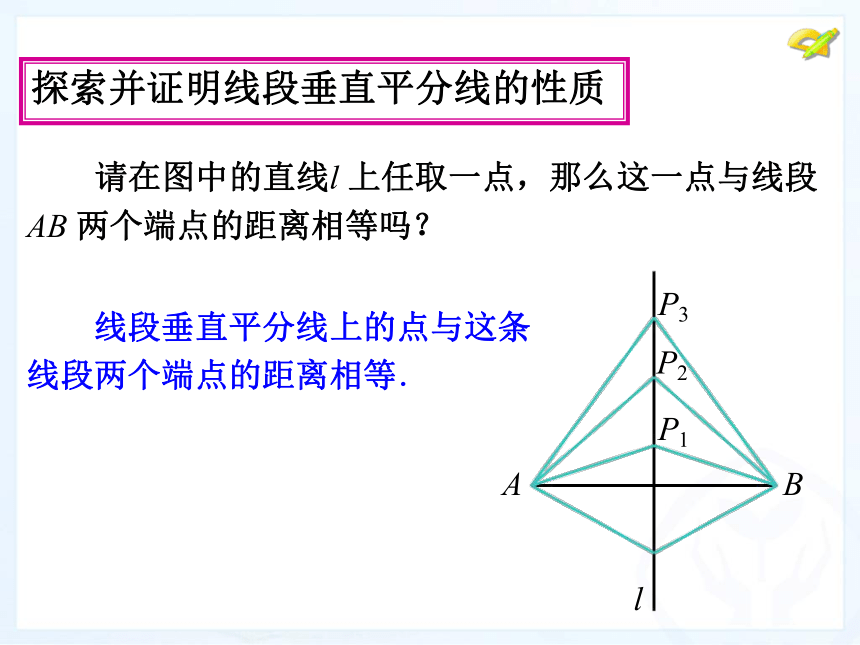
探索并证明线段垂直平分线的性质
请在图中的直线l 上任取一点,那么这一点与线段
AB 两个端点的距离相等吗?
线段垂直平分线上的点与这条
线段两个端点的距离相等.
A
B
l
P1
P2
P3
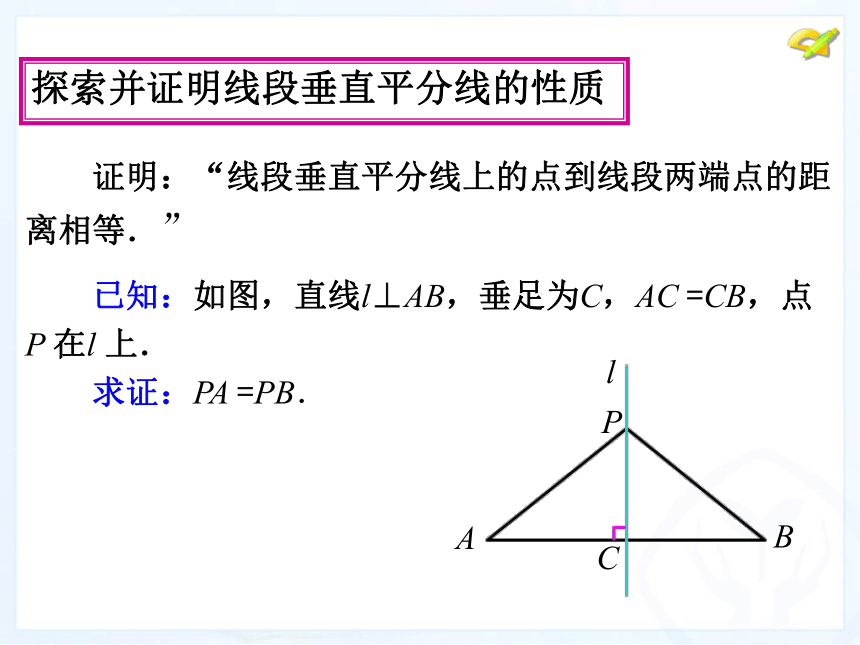
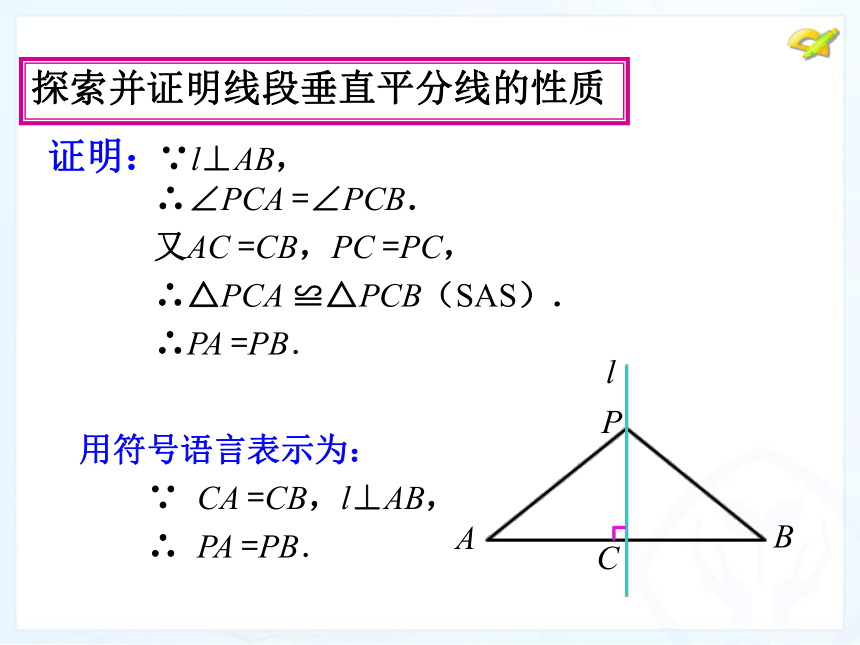
已知:如图,直线l⊥AB,垂足为C,AC =CB,点
P 在l 上.
求证:PA =PB.
探索并证明线段垂直平分线的性质
证明:“线段垂直平分线上的点到线段两端点的距
离相等.”
A
B
P
C
l
探索并证明线段垂直平分线的性质
用符号语言表示为:
∵ CA =CB,l⊥AB,
∴ PA =PB.
∴∠PCA =∠PCB.
又AC =CB,PC =PC,
∴△PCA ≌△PCB(SAS).
∴PA =PB.
A
B
P
C
l
证明:
∵l⊥AB,
探索并证明线段垂直平分线的性质
线段垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的距离
相等.
8
课堂练习
练习1 如图,在△ABC 中,BC =8,AB 的中垂线
交BC于D,AC 的中垂线交BC 与E,则△ADE 的周长等
于______.
A
B
C
D
E
∵ AD⊥BC,BD =DC,
∴ AD 是BC 的垂直平分线,
∴ AB =AC.
∵ 点C 在AE 的垂直平分线上,
∴ AC =CE.
课堂练习
练习2 如图,AD⊥BC,BD =DC,点C 在AE 的
垂直平分线上,AB,AC,CE 的长度有什么关系?
AB+BD与DE 有什么关系?
A
B
C
D
E
解:
∴ AB =AC =CE.
又 AB =CE,BD =DC,
∴ AB +BD =CD +CE.
即 AB +BD =DE .
探索并证明线段垂直平分线的判定
反过来,如果PA =PB,那么点P 是否在线段AB 的
垂直平分线上呢?
点P 在线段AB 的垂直平分线上.
已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平分线上.
P
A
B
C
探索并证明线段垂直平分线的判定
证明:过点P 作PC⊥AB,垂足为C.
则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上.
P
A
B
C
探索并证明线段垂直平分线的判定
∵ PA =PB,
∴ 点P 在AB 的垂直平分线上.
与一条线段两个端点距离相
等的点,在这条线段的垂直平分
线上.
P
A
B
C
用数学符号表示为:
这些点能组成什么几何图形?
探索并证明线段垂直平分线的判定
你能再找一些到线段AB 两端点的距离相等的点吗?
能找到多少个到线段AB 两端点距离相等的点?
在线段AB 的垂直平分线l 上的
点与A,B 的距离都相等;反过来,
与A,B 的距离相等的点都在直线l
上,所以直线l 可以看成与两点A、
B 的距离相等的所有点的集合.
P
A
B
C
结论:
线段垂直平分线上的点与这条线段两个端点的距离相等。
反之,与线段两个端点的距离相等的点在这条线段垂直平分线上。
所以,线段垂直平分线可以看作到线段两端的距离相等的所有点的集合。
解:∵ AB =AC,
∴ 点A 在BC 的垂直平分线.
∵ MB =MC,
∵ 点M 在BC 的垂直平分线上,
∴ 直线AM 是线段BC 的垂直平分线.
课堂练习
练习3 如图,AB =AC,MB =MC.直线AM 是线段
BC 的垂直平分线吗?
A
B
C
D
M
已知:直线AB和AB外一点C,
求作:AB的垂线,使它经过点C。
尺规作图
如何用尺规作图的方法经过直线外一点作已知直线
的垂线?
作法:
C
A
B
(1)任意取一点K,使点K和点C在AB的两旁,
.
K
(2)以点C为圆心,CK长半径作弧,交AB于点D和E,
(3)分别以点D和点E为圆心,大于DE长的一半为
半径作弧,两弧相交于点F.
D
E
⌒
⌒
F
(4)作直线CF,直线CF
就是所求的垂线。
课堂练习
练习4 如图,过点P 画∠AOB 两边的垂线,并和
同桌交流你的作图过程.
A
B
O
P
(1)本节课学习了哪些内容?
(2)线段垂直平分线的性质和判定是如何得到的?
两者之间有什么关系?
(3)如何判断一条直线是否是线段的垂直平分线?
课堂小结
角的平分线
O
D
E
A
B
P
C
定理1 在角的平分线上的点到这个角的两边的距离相等。
定理2 到一个角的两边的距离相等的点,在这个角的平分线上。
角的平分线是到角的两边距离相等的所有点的集合
线段的垂直平分线
定 理 线段垂直平分线上的点和这条线段两个端点的距离相等。
逆定理 和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合
A
B
M
N
P
点的集合是一条射线
点的集合是一条直线
布置作业
教科书习题13.1第6、9题.
分线的性质(1)
一、教学目标?
1、?能够利用尺规作已知线段的垂直平分线;?
2、?能已知底边及底边上的高用尺规作等腰三角形?
二、教学重、难点?、
1、重点:用尺规作已知线段垂直平分线?
2、难点:已知底边及底边上的高求作等腰三角形?
三、教学过程
轴对称图形
轴对称
区别
联系
1、对两个图形而言
2、指两个图形的相互关系
3、只有一条对称轴
1、对一个图形而言
2、指一个图形的特殊形状
3、至少有一条对称轴
1、沿某条直线对折后,直线两旁的部分都能重合;
2、若将成轴对称的两个图形看成一个整体,那么它就是一个轴对称图形;若把轴对称图形沿对称轴看成两个图形,那么这两个图形关于这条对称轴成轴对称.
3.都有对称轴
复习
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线
轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线
你能用不同的方法验证
这一结论吗?
探索并证明线段垂直平分线的性质
如图,直线l 垂直平分线段AB,P1,P2,P3,…是
l 上的点,请猜想点P1,P2,P3,… 到点A 与点B 的距
离之间的数量关系.
相等.
A
B
l
P1
P2
P3
探索并证明线段垂直平分线的性质
请在图中的直线l 上任取一点,那么这一点与线段
AB 两个端点的距离相等吗?
线段垂直平分线上的点与这条
线段两个端点的距离相等.
A
B
l
P1
P2
P3
已知:如图,直线l⊥AB,垂足为C,AC =CB,点
P 在l 上.
求证:PA =PB.
探索并证明线段垂直平分线的性质
证明:“线段垂直平分线上的点到线段两端点的距
离相等.”
A
B
P
C
l
探索并证明线段垂直平分线的性质
用符号语言表示为:
∵ CA =CB,l⊥AB,
∴ PA =PB.
∴∠PCA =∠PCB.
又AC =CB,PC =PC,
∴△PCA ≌△PCB(SAS).
∴PA =PB.
A
B
P
C
l
证明:
∵l⊥AB,
探索并证明线段垂直平分线的性质
线段垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的距离
相等.
8
课堂练习
练习1 如图,在△ABC 中,BC =8,AB 的中垂线
交BC于D,AC 的中垂线交BC 与E,则△ADE 的周长等
于______.
A
B
C
D
E
∵ AD⊥BC,BD =DC,
∴ AD 是BC 的垂直平分线,
∴ AB =AC.
∵ 点C 在AE 的垂直平分线上,
∴ AC =CE.
课堂练习
练习2 如图,AD⊥BC,BD =DC,点C 在AE 的
垂直平分线上,AB,AC,CE 的长度有什么关系?
AB+BD与DE 有什么关系?
A
B
C
D
E
解:
∴ AB =AC =CE.
又 AB =CE,BD =DC,
∴ AB +BD =CD +CE.
即 AB +BD =DE .
探索并证明线段垂直平分线的判定
反过来,如果PA =PB,那么点P 是否在线段AB 的
垂直平分线上呢?
点P 在线段AB 的垂直平分线上.
已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平分线上.
P
A
B
C
探索并证明线段垂直平分线的判定
证明:过点P 作PC⊥AB,垂足为C.
则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上.
P
A
B
C
探索并证明线段垂直平分线的判定
∵ PA =PB,
∴ 点P 在AB 的垂直平分线上.
与一条线段两个端点距离相
等的点,在这条线段的垂直平分
线上.
P
A
B
C
用数学符号表示为:
这些点能组成什么几何图形?
探索并证明线段垂直平分线的判定
你能再找一些到线段AB 两端点的距离相等的点吗?
能找到多少个到线段AB 两端点距离相等的点?
在线段AB 的垂直平分线l 上的
点与A,B 的距离都相等;反过来,
与A,B 的距离相等的点都在直线l
上,所以直线l 可以看成与两点A、
B 的距离相等的所有点的集合.
P
A
B
C
结论:
线段垂直平分线上的点与这条线段两个端点的距离相等。
反之,与线段两个端点的距离相等的点在这条线段垂直平分线上。
所以,线段垂直平分线可以看作到线段两端的距离相等的所有点的集合。
解:∵ AB =AC,
∴ 点A 在BC 的垂直平分线.
∵ MB =MC,
∵ 点M 在BC 的垂直平分线上,
∴ 直线AM 是线段BC 的垂直平分线.
课堂练习
练习3 如图,AB =AC,MB =MC.直线AM 是线段
BC 的垂直平分线吗?
A
B
C
D
M
已知:直线AB和AB外一点C,
求作:AB的垂线,使它经过点C。
尺规作图
如何用尺规作图的方法经过直线外一点作已知直线
的垂线?
作法:
C
A
B
(1)任意取一点K,使点K和点C在AB的两旁,
.
K
(2)以点C为圆心,CK长半径作弧,交AB于点D和E,
(3)分别以点D和点E为圆心,大于DE长的一半为
半径作弧,两弧相交于点F.
D
E
⌒
⌒
F
(4)作直线CF,直线CF
就是所求的垂线。
课堂练习
练习4 如图,过点P 画∠AOB 两边的垂线,并和
同桌交流你的作图过程.
A
B
O
P
(1)本节课学习了哪些内容?
(2)线段垂直平分线的性质和判定是如何得到的?
两者之间有什么关系?
(3)如何判断一条直线是否是线段的垂直平分线?
课堂小结
角的平分线
O
D
E
A
B
P
C
定理1 在角的平分线上的点到这个角的两边的距离相等。
定理2 到一个角的两边的距离相等的点,在这个角的平分线上。
角的平分线是到角的两边距离相等的所有点的集合
线段的垂直平分线
定 理 线段垂直平分线上的点和这条线段两个端点的距离相等。
逆定理 和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合
A
B
M
N
P
点的集合是一条射线
点的集合是一条直线
布置作业
教科书习题13.1第6、9题.
