人教版九年级数学下册 27.2.1相似三角形的判定3 课件(共19张ppt)
文档属性
| 名称 | 人教版九年级数学下册 27.2.1相似三角形的判定3 课件(共19张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 277.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览






文档简介
课前导入
06:00:49
27.2.1相似三角形的判定3
第二十七章 相似
06:00:49
06:00:49
学习目标
1.知道“两个角分别相等两个三角形相似”的判定
定理
2.会利用相似三角形判定定理解决问题
3.熟悉基本的相似模型
06:00:49
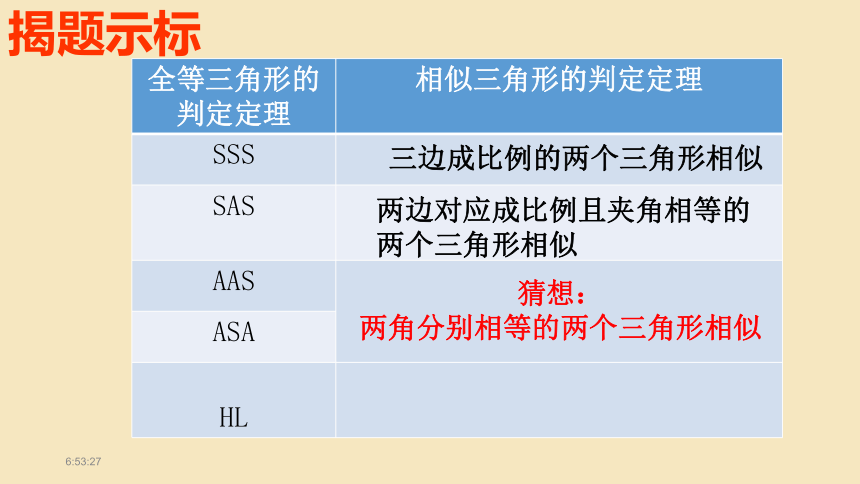
揭题示标
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}全等三角形的判定定理
相似三角形的判定定理
SSS
SAS
AAS
ASA
HL
三边成比例的两个三角形相似
两边对应成比例且夹角相等的两个三角形相似
猜想:
两角分别相等的两个三角形相似
06:00:49
在导学案上验证猜想:
两角分别相等的两个三角形相似
验证猜想:(时间3分钟)
自研共探1
06:00:49
证明猜想
如图,在△ABC和△A'B'C'中,∠A=∠A',∠B=∠B',求证△ABC∽△A'B'C'.
证明:在A'B'上截取点A'D=AB,过点D作DE//B'C'交A'C'于点E
∴△ABC∽△A'B'C'.
∵∠B=∠B',∴∠B=∠A'DE
又∵∠A=∠A',A'D=AB
∴△ABC≌△A'DE
则有:△A'B'C'∽△A'DE,∠A'DE=∠B'
两角分别相等的两个三角形相似
定理的数学符号语言
06:00:49
∵∠A=∠A',∠B=∠B'
∴△ABC∽△A'B'C'.
06:00:49
巩固新知
1.判断正误
(1)两个等腰三角形一定相似
(2)顶角相等的两个等腰三角形一定相似
(3)两个直角三角形一定相似
(4)有一个锐角对应相等的两个直角三角形一定相似
(5)两个等腰直角三角形一定相似
(6)两个等边三角形一定相似
×
√
×
√
√
√
认真自学课本35页例2,仔细看例2的解题过程
1.感受如何利用相似三角形判定定理解题的过程:
2.完成导学案上的习题1,2
注: 自学完成后,小组讨论。时间6分钟。
自研共探2
06:00:49
变式训练
1.如图,在△ABC中,D为AB边上一点,E为AC上一点。
(1)若∠ADE=∠C.证明:
证: ∵∠A=∠A,∠ADE=∠C
∴△ADE∽△ACB
∴
(2)要使△ABC∽△AED成立,还需要添加一个条
件为________.
三点定形法:横找竖找定相似
找准模型,类比做题
基础相似模型—“A”型
06:00:49
巩固提升
3.如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的高
发现与证明:
①求证AC?=AD.BD
②猜想:BC?_____BD.AB ,CD?___AD.BD
扩展与探究:
应用:
若AD=8,BD=2.则AC=_____,BC=_______,CD=_____
重点相似模型-射影模型
①求证:△ACD∽△ABC
②猜想:△CBD∽△ABC,△ACD∽△CBD成立吗?
06:00:49
巩固提升
发现与证明:
①求证:△ACD∽△ABC
②猜想:△CBD∽△ABC,△ACD∽△CBD成立吗?
∵∠A=∠A,∠ADC=∠ACB=90°
∴△ACD∽△ABC
证:
重点相似模型-射影模型
06:00:49
巩固提升
扩展与探究:
①求证:AC?=AD.AB
②猜想:BC?___BD.AB ,CD?___AD.BD成立
①证:由发现与证明知:△ABC∽△ACD
∴AC?=AD.BD
∴
遇等积,化比例,横找竖找定相似
=
=
重点相似模型-射影模型
06:00:49
巩固提升
应用:
若AD=8,BD=2.则AC=_____,BC=_______,CD=_____
熟记模型,快速做题
8
2
重点相似模型-射影模型
06:00:49
巧记模型—射影模型
AC?=AD.AB
BC?=BD.AB
CD?=AD.BD
二、相似模型
一 、相似三角形的判定定理
课堂小结
基础相似模型—A型,X型
重点相似模型—射影模型
A
B
C
D
E
一线三等角(直角)
06:00:49
解题小技巧:
1.找模型
2.遇等积,化比例,横找竖找定相似,
不相似,不着急,等线、等比和等积
06:00:49
课后作业
课本42页,习题27.2:4、5、7、13题
谢 谢
THANK YOU
06:00:49
06:00:49
27.2.1相似三角形的判定3
第二十七章 相似
06:00:49
06:00:49
学习目标
1.知道“两个角分别相等两个三角形相似”的判定
定理
2.会利用相似三角形判定定理解决问题
3.熟悉基本的相似模型
06:00:49
揭题示标
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}全等三角形的判定定理
相似三角形的判定定理
SSS
SAS
AAS
ASA
HL
三边成比例的两个三角形相似
两边对应成比例且夹角相等的两个三角形相似
猜想:
两角分别相等的两个三角形相似
06:00:49
在导学案上验证猜想:
两角分别相等的两个三角形相似
验证猜想:(时间3分钟)
自研共探1
06:00:49
证明猜想
如图,在△ABC和△A'B'C'中,∠A=∠A',∠B=∠B',求证△ABC∽△A'B'C'.
证明:在A'B'上截取点A'D=AB,过点D作DE//B'C'交A'C'于点E
∴△ABC∽△A'B'C'.
∵∠B=∠B',∴∠B=∠A'DE
又∵∠A=∠A',A'D=AB
∴△ABC≌△A'DE
则有:△A'B'C'∽△A'DE,∠A'DE=∠B'
两角分别相等的两个三角形相似
定理的数学符号语言
06:00:49
∵∠A=∠A',∠B=∠B'
∴△ABC∽△A'B'C'.
06:00:49
巩固新知
1.判断正误
(1)两个等腰三角形一定相似
(2)顶角相等的两个等腰三角形一定相似
(3)两个直角三角形一定相似
(4)有一个锐角对应相等的两个直角三角形一定相似
(5)两个等腰直角三角形一定相似
(6)两个等边三角形一定相似
×
√
×
√
√
√
认真自学课本35页例2,仔细看例2的解题过程
1.感受如何利用相似三角形判定定理解题的过程:
2.完成导学案上的习题1,2
注: 自学完成后,小组讨论。时间6分钟。
自研共探2
06:00:49
变式训练
1.如图,在△ABC中,D为AB边上一点,E为AC上一点。
(1)若∠ADE=∠C.证明:
证: ∵∠A=∠A,∠ADE=∠C
∴△ADE∽△ACB
∴
(2)要使△ABC∽△AED成立,还需要添加一个条
件为________.
三点定形法:横找竖找定相似
找准模型,类比做题
基础相似模型—“A”型
06:00:49
巩固提升
3.如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的高
发现与证明:
①求证AC?=AD.BD
②猜想:BC?_____BD.AB ,CD?___AD.BD
扩展与探究:
应用:
若AD=8,BD=2.则AC=_____,BC=_______,CD=_____
重点相似模型-射影模型
①求证:△ACD∽△ABC
②猜想:△CBD∽△ABC,△ACD∽△CBD成立吗?
06:00:49
巩固提升
发现与证明:
①求证:△ACD∽△ABC
②猜想:△CBD∽△ABC,△ACD∽△CBD成立吗?
∵∠A=∠A,∠ADC=∠ACB=90°
∴△ACD∽△ABC
证:
重点相似模型-射影模型
06:00:49
巩固提升
扩展与探究:
①求证:AC?=AD.AB
②猜想:BC?___BD.AB ,CD?___AD.BD成立
①证:由发现与证明知:△ABC∽△ACD
∴AC?=AD.BD
∴
遇等积,化比例,横找竖找定相似
=
=
重点相似模型-射影模型
06:00:49
巩固提升
应用:
若AD=8,BD=2.则AC=_____,BC=_______,CD=_____
熟记模型,快速做题
8
2
重点相似模型-射影模型
06:00:49
巧记模型—射影模型
AC?=AD.AB
BC?=BD.AB
CD?=AD.BD
二、相似模型
一 、相似三角形的判定定理
课堂小结
基础相似模型—A型,X型
重点相似模型—射影模型
A
B
C
D
E
一线三等角(直角)
06:00:49
解题小技巧:
1.找模型
2.遇等积,化比例,横找竖找定相似,
不相似,不着急,等线、等比和等积
06:00:49
课后作业
课本42页,习题27.2:4、5、7、13题
谢 谢
THANK YOU
06:00:49
