人教版七年级上册数学课件:3.4一元一次方程应用题总结(共25张ppt)
文档属性
| 名称 | 人教版七年级上册数学课件:3.4一元一次方程应用题总结(共25张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 867.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 21:44:48 | ||
图片预览







文档简介
3.4一元一次方程应用题专项
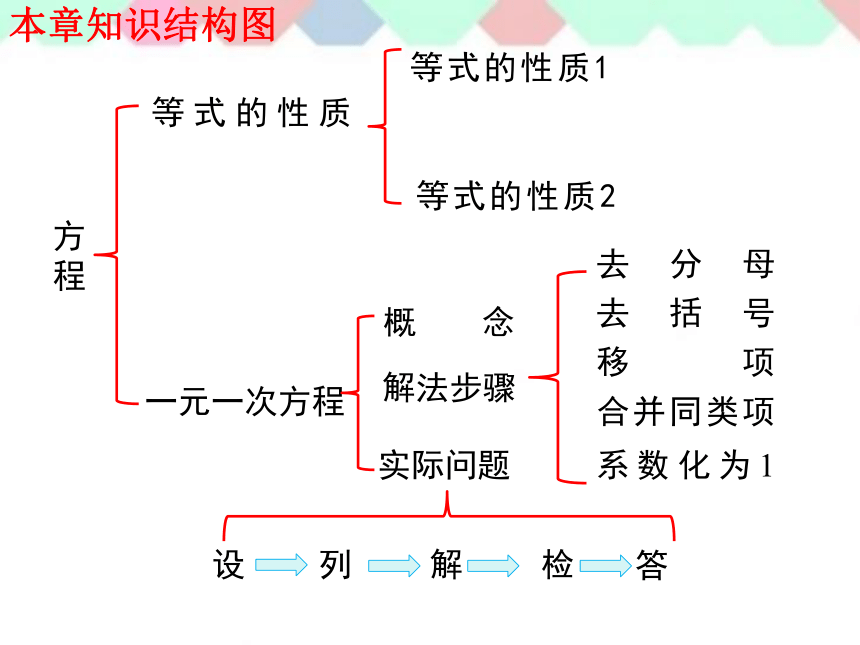
本章知识结构图
去括号
等式的性质
移项
合并同类项
概念
实际问题
去分母
系数化为1
解法步骤
一元一次方程
方程
等式的性质1
等式的性质2
设
列
解
检
答
列方程是解决实际问题的有效途径之一
1、审题:分析题意,找出图中的数量及其关系
2、设元:选择一个适当的未知数用字母表示(如x)
3、列方程:根据找出的相等关系列出方程
4、解方程:求出未知数的值
5、检验:检查求得的值是否正确和符合实际情形,
6、答:写出答案
基础题
已知矩形的周长为20厘米,设长为x厘米,则宽为( ).
A. 20-x B. 10-x C. 10-2x D. 20-2x
2.学生a人,以每10人为一组,其中有两组各少
1人,则学生共有( )组.
10a-2 B. 10-2a
C. 10-(2-a) D. (a +2)
B
D
数字问题
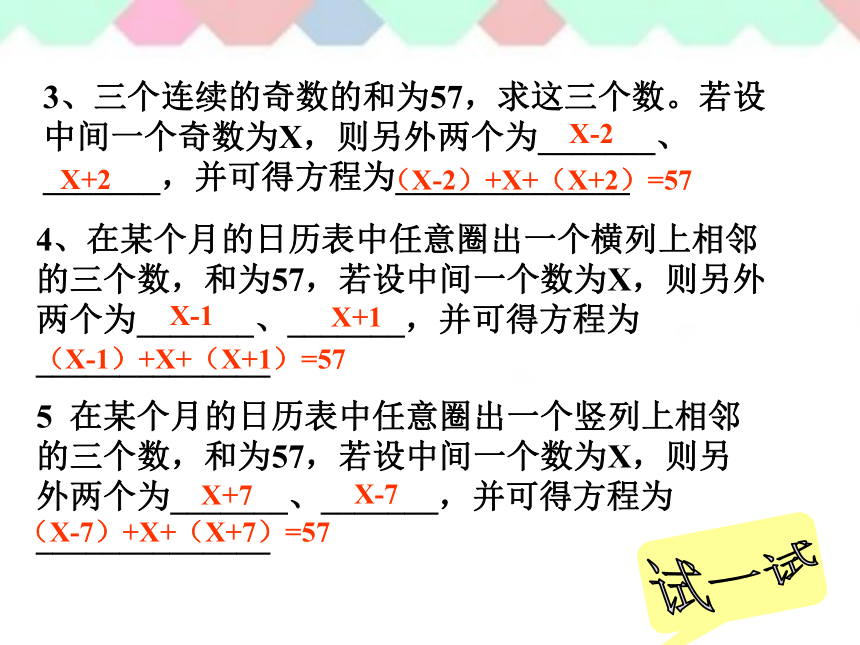
3、三个连续的奇数的和为57,求这三个数。若设中间一个奇数为X,则另外两个为_______、_______,并可得方程为______________
X-2
X+2
(X-2)+X+(X+2)=57
4、在某个月的日历表中任意圈出一个横列上相邻的三个数,和为57,若设中间一个数为X,则另外两个为_______、_______,并可得方程为______________
X-1
X+1
(X-1)+X+(X+1)=57
5 在某个月的日历表中任意圈出一个竖列上相邻的三个数,和为57,若设中间一个数为X,则另外两个为_______、_______,并可得方程为______________
X-7
X+7
(X-7)+X+(X+7)=57
综合题
1. 在课外活动中,张老师发现同学们的年龄大多是13岁.就问同学:“我今年45岁,几年以后你们的年龄是我年龄的三分之一?”
2. 小明的爸爸三年前为小明存了一份3000元的教育储蓄.今年到期时取出,得到的本息和为3243元,请你帮小明算一算这种储蓄的年利率.
3.小赵去商店买练习本,回来后问同学:“店主告诉我,如果多买一些就给我八折优惠.我就买了20本,结果便宜了1.60元.”你能算出练习本的单价吗?
行程问题
一、本课重点
1.基本关系式:_________________
2.基本类型: 相遇问题; 相距问题
3.基本分析方法:画示意图分析题意,分清速度及
时间,找等量关系(路程分成几部分).
4.航行问题的数量关系:
(1)顺流(风)航行的路程=逆流(风)航行的路程
(2)顺水(风)速度=_________________
逆水(风)速度=_________________
路程=速度X时间
静水(无风)速+水(风)速
静水(无风)速—水(风)速
二、基础题
1、甲的速度是每小时行4千米,则他x小时行( )千米.
2、乙3小时走了x千米,则他的速度( ).
3、甲每小时行4千米,乙每小时行5千米,则甲、 乙 一小时共行( )千米,y小时共行( )千米.
4、某一段路程 x 千米,如果火车以49千米/时的速度行驶,那么火车行完全程需要( )小时.
4X
9
9y
1、若明明以每小时4千米的速度行驶上学,哥哥半小时后发现明明忘了作业本,就骑车以每小时8千米追赶,问哥哥需要多长时间才可以送到作业?
解:设哥哥要X小时才可以送到作业本
8X = 4X + 4×0.5
解得 X = 0.5
答:哥哥要0.5小时才可以把作业送到
2、甲、乙两地路程为180千米,一人骑自行车从甲地出发每时走15千米,另一人骑摩托车从乙地出发,已知摩托车速度是自行车速度的3倍,若两人同时出发,相向而行,问经过多少时间两人相遇?
1. 甲、乙两地路程为180千米,一人骑自行车从甲地出发每时走15千米,另一人骑摩托车从乙地出发,已知摩托车速度是自行车速度的3倍,若两人同向而行,骑自行车在先且先出发2小时, 问摩托车经过多少时间追上自行车?
2.一架直升机在A,B两个城市之间飞行,顺风飞行需要4小时,逆风飞行需要5小时 .如果已知风速为30km/h,求A,B两个城市之间的距离.
三、综合题
一、基础题
1.某人用三天做零件330个,已知第二天比第一天多做3个,第三天做的是第二天的2倍少3个,则他第一天做了多少个零件?
解:设他第一天做零件 x 个,则他第二天做零件_____个,第三天做零件________个,根据“某人用三天做零件330个”
列出方程得:__________________________.
解这个方程得:______________.
答:他第一天做零件 ________ 个.
X+3
2(X+3)-3
2(X+3)-3+X+3+X=330
调配问题
2.初一甲、乙两班各有学生48人和52人,现从外校转来12人插入甲班 x 人,其余的都插入乙班,问插入后,
甲班有学生______人,乙班有学生_______人,若已知插入后,甲班学生人数的3倍比乙班学生人数的2倍还多4人,列出方程是: ________________.
48+X
52+(12-X)
3(48+X)=2[52+(12-X)]+4
3、甲仓库储粮35吨 ,乙仓库储粮19吨,现调粮食15吨,应分配给两仓库各多少吨,才能使得甲仓库的粮食数量是乙仓库的两倍?
分析 :若设应分给甲仓库粮食X吨,则数量关系如下表
原有粮食
新分给粮食
现有粮食
甲仓库
35
X
35+X
乙仓库
19
(15-X)
19+(15-X)
相等关系为 :
甲仓库现有粮食的重量=2×乙仓库现有粮食的重量
解 :设应分给甲仓库粮食X吨,则应分给乙仓库粮食(15-X)吨。
依题意得
解之得 X=11
则 15-X=4
答 :应分给甲仓库11吨粮食,分给乙仓库4吨粮食。
二、综合题
1、配制一种混凝土,水泥、沙、石子、水的质量比是1:3:10:4,要配制这种混凝土360千克,各种原料分别需要多少千克?
2. 为鼓励节约用水,某地按以下规定收取每月的水费:如果每月每户用水不超过20吨,那么每吨水按1.2元收费;如果每月每户用水超过20吨,那么超过的部分按每吨2元收费。若某用户五月份的水费为平均每吨1.5元,问,该用户五月份应交水费多少元?
3. 甲种糖果的单价是每千克20元,乙种糖果的单价是每千克15元,若要配制200千克单价为每千克18元的混合糖果,并使之和分别销售两种糖果的总收入保持不变,问需甲、乙两种糖果各多少千克?
一、基础题
1.做某件工作,甲单独做要8时才能完成,乙单独做要12时才能完成,问:
①甲做1时完成全部工作量的几分之几?_____ 。
②乙做1时完成全部工作量的几分之几?_____ 。
③甲、乙合做1时完成全部工作量的几分之几?_____ 。
④甲做x时完成全部工作量的几分之几?_____ 。
工程问题
2、一个工人加工一批零件,限期完成,若他每小时做10个,到期可超额完成3个,若每小时做11个,则可提前1小时完成任务,问他共要加工多少个零件,限期多少小时完成?
分析 :相等关系为
按第一种工作效率所做的零件数=按第二种工作效率所做的零件数
解 :设限期X小时完成,则依题意得
解之得 X=8
则零件总数为 10X-3=77
答 :共要加工零件77个,限期8小时完成。
二、综合题
1.一项工程,甲单独做要10天完成,乙单独做要15天完成,两人合做4天后,剩下的部分由乙单独做,还需要几天完成?
2.食堂存煤若干吨,原来每天烧煤4吨,用去15吨后,改进设备,耗煤量改为原来的一半,结果多烧了10天,求原存煤量.
3.一水池,单开进水管3小时可将水池注满,单开出水管4小时可将满池水放完。现对空水池先打开进水管2小时,然后打开出水管,使进水管、出水管一起开放,问再过几小时可将水池注满?
4.一项工程,甲单独做要10天完成,乙单独做要15天完成,甲单独做5天,然后甲、乙合作完成,共得到1000元,如果按照每人完成工作量计算报酬,那么甲、乙两人该如何分配?
一、基础题
1.某商品按定价的八折出售,售价14.80元, 则原定价是________元。
2.盛超把爸、妈给的压岁钱1000元按定期一年存入银行。当时一年期定期存款的年利率为1.98%,利息税的税率为20%。到期支取时,利息为_______
税后利息________,小明实得本利和为__________.
销售问题
3.A、B两家售货亭以同样价格出售商品,一星期后A家把价格降低了10%,再过一个星期又提高20%,B家只是在两星期后才提价10%,两星期后_____家售货亭的售价低。
4.某服装商贩同时卖出两套服装,每套均卖168元,以成本计算其中一套盈利20%,另一套亏本20%,则这次出售商贩__________(盈利或亏本)
二、综合题
1.一商店将某型号彩电按原售价提高40%,然后在广告中写上“大酬宾,八折优惠”,经顾客投诉后,执法部门按已得非法收入10倍处以每台2700元的罚款,求每台彩电的原售价?
2.一种商品的买入单价为1500元,如果出售一件商品获得的毛利润是卖出单价的15%,那么这种商品出售单价应定为多少元?(精确到1元)
其它类型应用题
(1)和差倍分问题 :
例1 :一桶煤油连桶重8公斤,用去一半煤油后,连桶重4.5公斤,求桶中原有煤油多少公斤及桶重。
分析 :相等关系为
用去的煤油的重量+余下的油量及桶重=原来连桶带油的重量
解 :设原有煤油x公斤
依题意得
解之得 x=7
则桶重为 8-x=1
答 :原有煤油7公斤,桶重为1公斤。
(2)形积变换问题
例2 :一个长方形的长比宽多2㎝,若把它的长和宽分别增加3㎝,则面积增加45㎝2,求原长方形的长与宽。
分析 :若设原长方形的宽为x 厘米,画图如下
x
X+2
X+3
(X+2)+3
可知相等关系为 :
原长方形的面积+45 ㎝ 2 =新长方形的面积
解 :设原长方形的宽为x 厘米,则其长为(x+2)厘米。 依题意得
解之得 x=5
则原长方形的长为 x+2=7
答 :原长方形的长为7㎝,宽为5㎝。
(3)、数字问题
例7 :一个两位数的十位上的数是个位上的数的两倍,若把两个数字对调,则新得到的两位数比原两位数小36,求原两位数。
分析 :题中数量关系如下表 (若设原数的个位数字为X)
十位数字
个位数字
本数
原两位数
2 X
X
20X+X
新两位数
X
2X
10X+2X
解 :设原两位数的个位数字为X,则其十位数字为2X。
列出方程为
(10x+2x)+36=20x+x
解之得 X=4
则原数的十位数字为 2X=8
答 :原两位数是84。
可知相等关系为:原两位数+36=新两位数
本章知识结构图
去括号
等式的性质
移项
合并同类项
概念
实际问题
去分母
系数化为1
解法步骤
一元一次方程
方程
等式的性质1
等式的性质2
设
列
解
检
答
列方程是解决实际问题的有效途径之一
1、审题:分析题意,找出图中的数量及其关系
2、设元:选择一个适当的未知数用字母表示(如x)
3、列方程:根据找出的相等关系列出方程
4、解方程:求出未知数的值
5、检验:检查求得的值是否正确和符合实际情形,
6、答:写出答案
基础题
已知矩形的周长为20厘米,设长为x厘米,则宽为( ).
A. 20-x B. 10-x C. 10-2x D. 20-2x
2.学生a人,以每10人为一组,其中有两组各少
1人,则学生共有( )组.
10a-2 B. 10-2a
C. 10-(2-a) D. (a +2)
B
D
数字问题
3、三个连续的奇数的和为57,求这三个数。若设中间一个奇数为X,则另外两个为_______、_______,并可得方程为______________
X-2
X+2
(X-2)+X+(X+2)=57
4、在某个月的日历表中任意圈出一个横列上相邻的三个数,和为57,若设中间一个数为X,则另外两个为_______、_______,并可得方程为______________
X-1
X+1
(X-1)+X+(X+1)=57
5 在某个月的日历表中任意圈出一个竖列上相邻的三个数,和为57,若设中间一个数为X,则另外两个为_______、_______,并可得方程为______________
X-7
X+7
(X-7)+X+(X+7)=57
综合题
1. 在课外活动中,张老师发现同学们的年龄大多是13岁.就问同学:“我今年45岁,几年以后你们的年龄是我年龄的三分之一?”
2. 小明的爸爸三年前为小明存了一份3000元的教育储蓄.今年到期时取出,得到的本息和为3243元,请你帮小明算一算这种储蓄的年利率.
3.小赵去商店买练习本,回来后问同学:“店主告诉我,如果多买一些就给我八折优惠.我就买了20本,结果便宜了1.60元.”你能算出练习本的单价吗?
行程问题
一、本课重点
1.基本关系式:_________________
2.基本类型: 相遇问题; 相距问题
3.基本分析方法:画示意图分析题意,分清速度及
时间,找等量关系(路程分成几部分).
4.航行问题的数量关系:
(1)顺流(风)航行的路程=逆流(风)航行的路程
(2)顺水(风)速度=_________________
逆水(风)速度=_________________
路程=速度X时间
静水(无风)速+水(风)速
静水(无风)速—水(风)速
二、基础题
1、甲的速度是每小时行4千米,则他x小时行( )千米.
2、乙3小时走了x千米,则他的速度( ).
3、甲每小时行4千米,乙每小时行5千米,则甲、 乙 一小时共行( )千米,y小时共行( )千米.
4、某一段路程 x 千米,如果火车以49千米/时的速度行驶,那么火车行完全程需要( )小时.
4X
9
9y
1、若明明以每小时4千米的速度行驶上学,哥哥半小时后发现明明忘了作业本,就骑车以每小时8千米追赶,问哥哥需要多长时间才可以送到作业?
解:设哥哥要X小时才可以送到作业本
8X = 4X + 4×0.5
解得 X = 0.5
答:哥哥要0.5小时才可以把作业送到
2、甲、乙两地路程为180千米,一人骑自行车从甲地出发每时走15千米,另一人骑摩托车从乙地出发,已知摩托车速度是自行车速度的3倍,若两人同时出发,相向而行,问经过多少时间两人相遇?
1. 甲、乙两地路程为180千米,一人骑自行车从甲地出发每时走15千米,另一人骑摩托车从乙地出发,已知摩托车速度是自行车速度的3倍,若两人同向而行,骑自行车在先且先出发2小时, 问摩托车经过多少时间追上自行车?
2.一架直升机在A,B两个城市之间飞行,顺风飞行需要4小时,逆风飞行需要5小时 .如果已知风速为30km/h,求A,B两个城市之间的距离.
三、综合题
一、基础题
1.某人用三天做零件330个,已知第二天比第一天多做3个,第三天做的是第二天的2倍少3个,则他第一天做了多少个零件?
解:设他第一天做零件 x 个,则他第二天做零件_____个,第三天做零件________个,根据“某人用三天做零件330个”
列出方程得:__________________________.
解这个方程得:______________.
答:他第一天做零件 ________ 个.
X+3
2(X+3)-3
2(X+3)-3+X+3+X=330
调配问题
2.初一甲、乙两班各有学生48人和52人,现从外校转来12人插入甲班 x 人,其余的都插入乙班,问插入后,
甲班有学生______人,乙班有学生_______人,若已知插入后,甲班学生人数的3倍比乙班学生人数的2倍还多4人,列出方程是: ________________.
48+X
52+(12-X)
3(48+X)=2[52+(12-X)]+4
3、甲仓库储粮35吨 ,乙仓库储粮19吨,现调粮食15吨,应分配给两仓库各多少吨,才能使得甲仓库的粮食数量是乙仓库的两倍?
分析 :若设应分给甲仓库粮食X吨,则数量关系如下表
原有粮食
新分给粮食
现有粮食
甲仓库
35
X
35+X
乙仓库
19
(15-X)
19+(15-X)
相等关系为 :
甲仓库现有粮食的重量=2×乙仓库现有粮食的重量
解 :设应分给甲仓库粮食X吨,则应分给乙仓库粮食(15-X)吨。
依题意得
解之得 X=11
则 15-X=4
答 :应分给甲仓库11吨粮食,分给乙仓库4吨粮食。
二、综合题
1、配制一种混凝土,水泥、沙、石子、水的质量比是1:3:10:4,要配制这种混凝土360千克,各种原料分别需要多少千克?
2. 为鼓励节约用水,某地按以下规定收取每月的水费:如果每月每户用水不超过20吨,那么每吨水按1.2元收费;如果每月每户用水超过20吨,那么超过的部分按每吨2元收费。若某用户五月份的水费为平均每吨1.5元,问,该用户五月份应交水费多少元?
3. 甲种糖果的单价是每千克20元,乙种糖果的单价是每千克15元,若要配制200千克单价为每千克18元的混合糖果,并使之和分别销售两种糖果的总收入保持不变,问需甲、乙两种糖果各多少千克?
一、基础题
1.做某件工作,甲单独做要8时才能完成,乙单独做要12时才能完成,问:
①甲做1时完成全部工作量的几分之几?_____ 。
②乙做1时完成全部工作量的几分之几?_____ 。
③甲、乙合做1时完成全部工作量的几分之几?_____ 。
④甲做x时完成全部工作量的几分之几?_____ 。
工程问题
2、一个工人加工一批零件,限期完成,若他每小时做10个,到期可超额完成3个,若每小时做11个,则可提前1小时完成任务,问他共要加工多少个零件,限期多少小时完成?
分析 :相等关系为
按第一种工作效率所做的零件数=按第二种工作效率所做的零件数
解 :设限期X小时完成,则依题意得
解之得 X=8
则零件总数为 10X-3=77
答 :共要加工零件77个,限期8小时完成。
二、综合题
1.一项工程,甲单独做要10天完成,乙单独做要15天完成,两人合做4天后,剩下的部分由乙单独做,还需要几天完成?
2.食堂存煤若干吨,原来每天烧煤4吨,用去15吨后,改进设备,耗煤量改为原来的一半,结果多烧了10天,求原存煤量.
3.一水池,单开进水管3小时可将水池注满,单开出水管4小时可将满池水放完。现对空水池先打开进水管2小时,然后打开出水管,使进水管、出水管一起开放,问再过几小时可将水池注满?
4.一项工程,甲单独做要10天完成,乙单独做要15天完成,甲单独做5天,然后甲、乙合作完成,共得到1000元,如果按照每人完成工作量计算报酬,那么甲、乙两人该如何分配?
一、基础题
1.某商品按定价的八折出售,售价14.80元, 则原定价是________元。
2.盛超把爸、妈给的压岁钱1000元按定期一年存入银行。当时一年期定期存款的年利率为1.98%,利息税的税率为20%。到期支取时,利息为_______
税后利息________,小明实得本利和为__________.
销售问题
3.A、B两家售货亭以同样价格出售商品,一星期后A家把价格降低了10%,再过一个星期又提高20%,B家只是在两星期后才提价10%,两星期后_____家售货亭的售价低。
4.某服装商贩同时卖出两套服装,每套均卖168元,以成本计算其中一套盈利20%,另一套亏本20%,则这次出售商贩__________(盈利或亏本)
二、综合题
1.一商店将某型号彩电按原售价提高40%,然后在广告中写上“大酬宾,八折优惠”,经顾客投诉后,执法部门按已得非法收入10倍处以每台2700元的罚款,求每台彩电的原售价?
2.一种商品的买入单价为1500元,如果出售一件商品获得的毛利润是卖出单价的15%,那么这种商品出售单价应定为多少元?(精确到1元)
其它类型应用题
(1)和差倍分问题 :
例1 :一桶煤油连桶重8公斤,用去一半煤油后,连桶重4.5公斤,求桶中原有煤油多少公斤及桶重。
分析 :相等关系为
用去的煤油的重量+余下的油量及桶重=原来连桶带油的重量
解 :设原有煤油x公斤
依题意得
解之得 x=7
则桶重为 8-x=1
答 :原有煤油7公斤,桶重为1公斤。
(2)形积变换问题
例2 :一个长方形的长比宽多2㎝,若把它的长和宽分别增加3㎝,则面积增加45㎝2,求原长方形的长与宽。
分析 :若设原长方形的宽为x 厘米,画图如下
x
X+2
X+3
(X+2)+3
可知相等关系为 :
原长方形的面积+45 ㎝ 2 =新长方形的面积
解 :设原长方形的宽为x 厘米,则其长为(x+2)厘米。 依题意得
解之得 x=5
则原长方形的长为 x+2=7
答 :原长方形的长为7㎝,宽为5㎝。
(3)、数字问题
例7 :一个两位数的十位上的数是个位上的数的两倍,若把两个数字对调,则新得到的两位数比原两位数小36,求原两位数。
分析 :题中数量关系如下表 (若设原数的个位数字为X)
十位数字
个位数字
本数
原两位数
2 X
X
20X+X
新两位数
X
2X
10X+2X
解 :设原两位数的个位数字为X,则其十位数字为2X。
列出方程为
(10x+2x)+36=20x+x
解之得 X=4
则原数的十位数字为 2X=8
答 :原两位数是84。
可知相等关系为:原两位数+36=新两位数
