圆的有关计算课件
图片预览

文档简介
(共14张PPT)
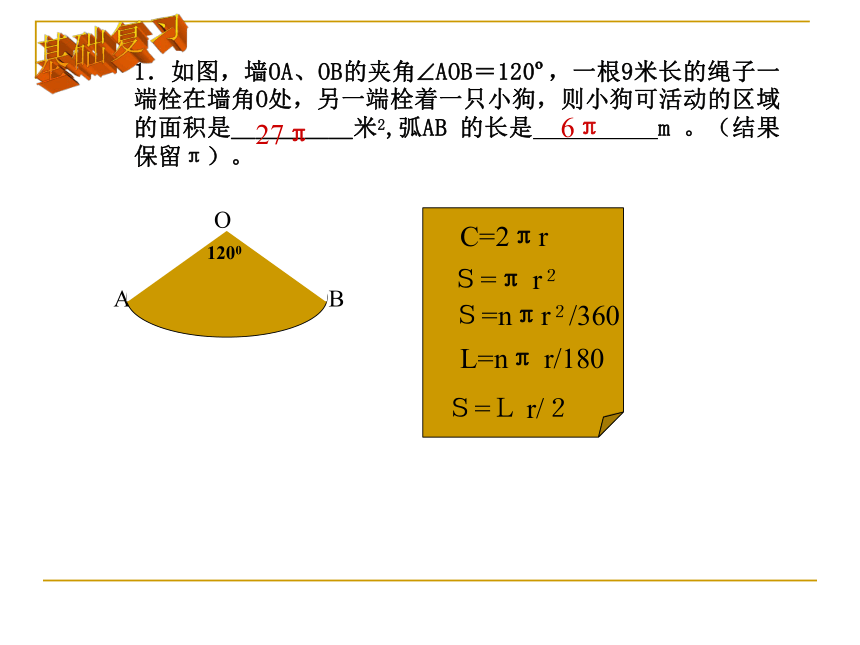
S=L r/2
1.如图,墙OA、OB的夹角 AOB=120 ,一根9米长的绳子一端栓在墙角O处,另一端栓着一只小狗,则小狗可活动的区域的面积是_____米2,弧AB 的长是 m 。(结果保留π)。
B
A
O
1200
S=nπr2/360
L=nπ r/180
S=π r2
C=2πr
27π
6π
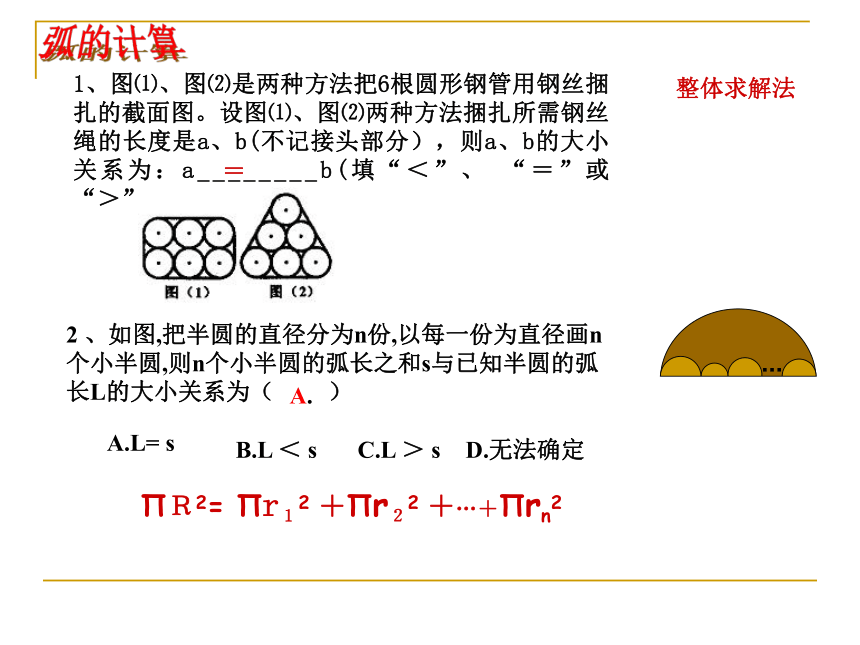
1、图⑴、图⑵是两种方法把6根圆形钢管用钢丝捆扎的截面图。设图⑴、图⑵两种方法捆扎所需钢丝绳的长度是a、b(不记接头部分),则a、b的大小关系为:a________b(填“<”、 “=”或“>”)。
=
2 、如图,把半圆的直径分为n份,以每一份为直径画n个小半圆,则n个小半圆的弧长之和s与已知半圆的弧长L的大小关系为( )
A.L= s
B.L < s
C.L > s
D.无法确定
A.
整体求解法
ΠR2= Πr12 +Πr22 +…+Πrn2
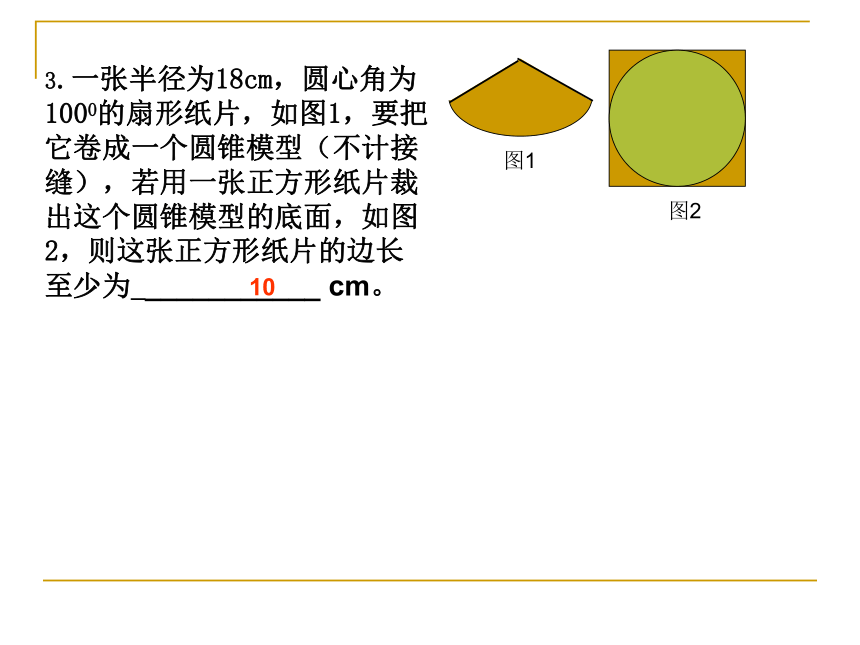
3.一张半径为18cm,圆心角为1000的扇形纸片,如图1,要把它卷成一个圆锥模型(不计接缝),若用一张正方形纸片裁出这个圆锥模型的底面,如图2,则这张正方形纸片的边长至少为____________ cm。
图1
图2
10
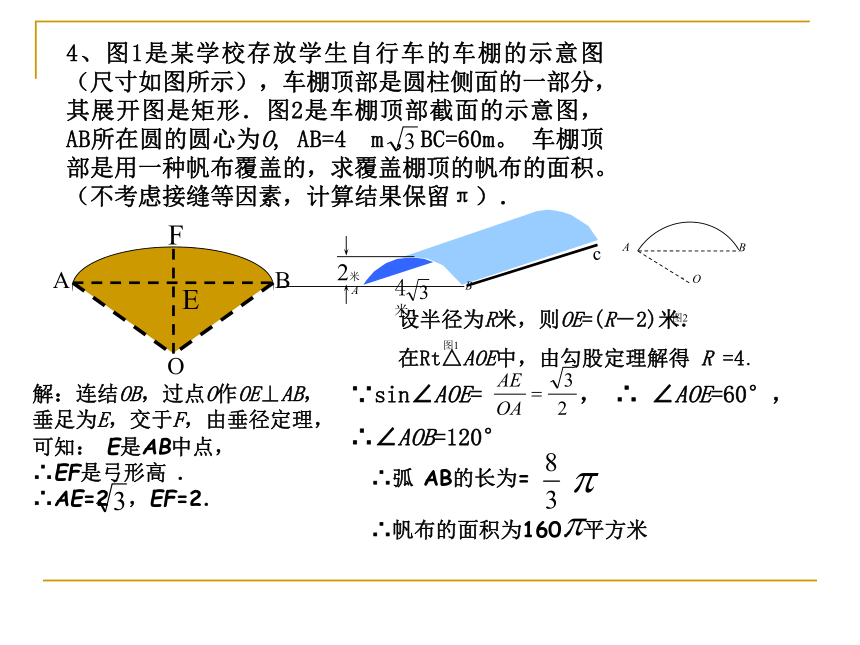
4、图1是某学校存放学生自行车的车棚的示意图(尺寸如图所示),车棚顶部是圆柱侧面的一部分,其展开图是矩形.图2是车棚顶部截面的示意图,AB所在圆的圆心为O, AB=4 m , BC=60m。 车棚顶部是用一种帆布覆盖的,求覆盖棚顶的帆布的面积。(不考虑接缝等因素,计算结果保留π).
B
A
O
E
F
c
O
B
A
·
图2
图1
A
B
2米
4 米
设半径为R米,则OE=(R-2)米.
在Rt△AOE中,由勾股定理解得 R =4.
∵sin∠AOE= , ∴ ∠AOE=60°,
∴∠AOB=120°
∴弧 AB的长为=
∴帆布的面积为160.平方米
解:连结OB,过点O作OE⊥AB,垂足为E,交于F,由垂径定理,可知: E是AB中点,
∴EF是弓形高 .
∴AE=2 ,EF=2.
1.如图,半径为2的两圆⊙O1和⊙O2均与Y轴相切于点O,反比例函数 ( )的图像与两圆分别交于点A,B,C,D,则图中阴影部分的面积是 .
x
C
D
A
B
O
O2
O1
y
-2
2
2π
图2
2.如图2所示,分别以n边形的顶点为圆心,以单位1为半径画圆,则图中阴影部分的面积之和为 个平方单位.
π
整体求解法
割补法
3.如图,从P点引⊙O的两切线PA、PB,A、B为切点,已知⊙O的半径为2,∠P=60°,则图中阴影部分的面积为 。
(第16题图)
A
B
P
O
S阴影=S△AOP-S△BOP-S扇形
4.如图1,小丽同学设计的图案《我的宝贝》,图案的一部分是斜边为12 cm 的等腰直角三角形,其余是分别以其它三边为直径作的半圆,则图中阴影部分的面积为____________。
36cm 2
S阴影=2S小半圆-(S大半圆-S△)
S半圆= S小半圆+ S小半圆
4 -4 π/3
A
B
O1
O2
1.如图, ⊙O1的弦AB是⊙O2 的切线,且AB// O1 O2,如果AB=12cm,那么阴影部分的面积是( )
A.6π
D.无法计算
B.12π
C.36π
2.如图,半圆O的直径AB=12,P为AB上一点,
点C,D为半圆0的三等分点,则阴影部分的
面积等于_______.
C
D
A
P
O
B
图(9)
C
6π
O1
A
B
平移法
等面积代换法
图1
4、已知,点P是正方形ABCD内的一点,连PA、PB、PC.(1)将△PAB绕点B顺时针旋转90°到△P′CB的位置(如图1).①设AB的长为a,PB的长为b(b3、如图(一),水平地面上有一面积为30
平方公分的灰色扇形OAB,其中OA的长度
为6公分,且OA与地面垂直。若在没有滑动
的情况下,将图(一)的扇形向右滚动至OB
垂直地面为止,如图(二)所示,
则O点移动____________ 公分。
A
B
O
圗(一)
A
B
O
圗(二)
10π
S阴影= π(a2- b2)/4
旋转法
5 、如图,A、B、C、D是圆周上的四点,
AB
CD
+
AC
BD
+
=
且弦AB=8,弦CD=6,
则图中阴影部分的面积为____________。
B
A
C
D
B
A
C
(D)
25π-24
已知:B、C是线段AD上的两点,且AB=CD,分别以AB、BC、CD、AD为直径作四个半圆,得到一个如图所示的轴对称图形.此图的对称轴分别交其中两个半圆于M、N,交AD于O.
若AD=16,AB=2r(0<r<4),回答下列问题:
(1)用含r的代数式表示BC=____________,MN=____________;
(2)设以MN为直径的圆的面积为S,阴影部分的面积为S阴影,请通过计算填写下表:
r S S阴影
r=1 49π
r=2 36π
r=3 25π
A
B
C
D
O
M
N
(3)由此猜想S与S阴影的大小关系。
16-2r
16-4r
49π
36π
25π
S= S阴影
小结:
S=L r/2
S=nπr2/360
L=nπ r/180
S=π r2
C=2πr
1计算公式
2数学思想
转化的思想
割补法
平移法
等面积代换法
旋转法
整体求解法
作业:略。
3方法
S=L r/2
1.如图,墙OA、OB的夹角 AOB=120 ,一根9米长的绳子一端栓在墙角O处,另一端栓着一只小狗,则小狗可活动的区域的面积是_____米2,弧AB 的长是 m 。(结果保留π)。
B
A
O
1200
S=nπr2/360
L=nπ r/180
S=π r2
C=2πr
27π
6π
1、图⑴、图⑵是两种方法把6根圆形钢管用钢丝捆扎的截面图。设图⑴、图⑵两种方法捆扎所需钢丝绳的长度是a、b(不记接头部分),则a、b的大小关系为:a________b(填“<”、 “=”或“>”)。
=
2 、如图,把半圆的直径分为n份,以每一份为直径画n个小半圆,则n个小半圆的弧长之和s与已知半圆的弧长L的大小关系为( )
A.L= s
B.L < s
C.L > s
D.无法确定
A.
整体求解法
ΠR2= Πr12 +Πr22 +…+Πrn2
3.一张半径为18cm,圆心角为1000的扇形纸片,如图1,要把它卷成一个圆锥模型(不计接缝),若用一张正方形纸片裁出这个圆锥模型的底面,如图2,则这张正方形纸片的边长至少为____________ cm。
图1
图2
10
4、图1是某学校存放学生自行车的车棚的示意图(尺寸如图所示),车棚顶部是圆柱侧面的一部分,其展开图是矩形.图2是车棚顶部截面的示意图,AB所在圆的圆心为O, AB=4 m , BC=60m。 车棚顶部是用一种帆布覆盖的,求覆盖棚顶的帆布的面积。(不考虑接缝等因素,计算结果保留π).
B
A
O
E
F
c
O
B
A
·
图2
图1
A
B
2米
4 米
设半径为R米,则OE=(R-2)米.
在Rt△AOE中,由勾股定理解得 R =4.
∵sin∠AOE= , ∴ ∠AOE=60°,
∴∠AOB=120°
∴弧 AB的长为=
∴帆布的面积为160.平方米
解:连结OB,过点O作OE⊥AB,垂足为E,交于F,由垂径定理,可知: E是AB中点,
∴EF是弓形高 .
∴AE=2 ,EF=2.
1.如图,半径为2的两圆⊙O1和⊙O2均与Y轴相切于点O,反比例函数 ( )的图像与两圆分别交于点A,B,C,D,则图中阴影部分的面积是 .
x
C
D
A
B
O
O2
O1
y
-2
2
2π
图2
2.如图2所示,分别以n边形的顶点为圆心,以单位1为半径画圆,则图中阴影部分的面积之和为 个平方单位.
π
整体求解法
割补法
3.如图,从P点引⊙O的两切线PA、PB,A、B为切点,已知⊙O的半径为2,∠P=60°,则图中阴影部分的面积为 。
(第16题图)
A
B
P
O
S阴影=S△AOP-S△BOP-S扇形
4.如图1,小丽同学设计的图案《我的宝贝》,图案的一部分是斜边为12 cm 的等腰直角三角形,其余是分别以其它三边为直径作的半圆,则图中阴影部分的面积为____________。
36cm 2
S阴影=2S小半圆-(S大半圆-S△)
S半圆= S小半圆+ S小半圆
4 -4 π/3
A
B
O1
O2
1.如图, ⊙O1的弦AB是⊙O2 的切线,且AB// O1 O2,如果AB=12cm,那么阴影部分的面积是( )
A.6π
D.无法计算
B.12π
C.36π
2.如图,半圆O的直径AB=12,P为AB上一点,
点C,D为半圆0的三等分点,则阴影部分的
面积等于_______.
C
D
A
P
O
B
图(9)
C
6π
O1
A
B
平移法
等面积代换法
图1
4、已知,点P是正方形ABCD内的一点,连PA、PB、PC.(1)将△PAB绕点B顺时针旋转90°到△P′CB的位置(如图1).①设AB的长为a,PB的长为b(b
平方公分的灰色扇形OAB,其中OA的长度
为6公分,且OA与地面垂直。若在没有滑动
的情况下,将图(一)的扇形向右滚动至OB
垂直地面为止,如图(二)所示,
则O点移动____________ 公分。
A
B
O
圗(一)
A
B
O
圗(二)
10π
S阴影= π(a2- b2)/4
旋转法
5 、如图,A、B、C、D是圆周上的四点,
AB
CD
+
AC
BD
+
=
且弦AB=8,弦CD=6,
则图中阴影部分的面积为____________。
B
A
C
D
B
A
C
(D)
25π-24
已知:B、C是线段AD上的两点,且AB=CD,分别以AB、BC、CD、AD为直径作四个半圆,得到一个如图所示的轴对称图形.此图的对称轴分别交其中两个半圆于M、N,交AD于O.
若AD=16,AB=2r(0<r<4),回答下列问题:
(1)用含r的代数式表示BC=____________,MN=____________;
(2)设以MN为直径的圆的面积为S,阴影部分的面积为S阴影,请通过计算填写下表:
r S S阴影
r=1 49π
r=2 36π
r=3 25π
A
B
C
D
O
M
N
(3)由此猜想S与S阴影的大小关系。
16-2r
16-4r
49π
36π
25π
S= S阴影
小结:
S=L r/2
S=nπr2/360
L=nπ r/180
S=π r2
C=2πr
1计算公式
2数学思想
转化的思想
割补法
平移法
等面积代换法
旋转法
整体求解法
作业:略。
3方法
