2020-2021学年苏科版九年级数学上册2.4.3 圆内接四边形(word版含答案)
文档属性
| 名称 | 2020-2021学年苏科版九年级数学上册2.4.3 圆内接四边形(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 712.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 23:16:47 | ||
图片预览


文档简介
2.4
圆周角2.4.3
圆内接四边形
一、选择题(共7小题;共35分)
1.
已知四边形
内接于圆,则
,,,
的度数之比可能是
A.
B.
C.
D.
2.
下列关于圆内接四边形叙述正确的有
①圆内接四边形的一个外角等于它的内对角;
②圆内接四边形对角相等;
③圆内接四边形中不相邻的两个内角互补;
④在圆内部的四边形叫圆内接四边形.
A.
个
B.
个
C.
个
D.
个
3.
如图,四边形
为
的内接四边形,已知
,则
A.
B.
C.
D.
4.
平行四边形的四个顶点在同一个圆上,则该平行四边形一定是
A.
正方形
B.
菱形
C.
矩形
D.
梯形
5.
如图,点
,,,
都在
上,,,,则
的直径的长是
A.
B.
C.
D.
6.
如图,四边形
内接于
,四边形
是平行四边形,则
A.
B.
C.
D.
7.
如图,
过原点,且与两坐标轴分别交于点
,点
,点
的坐标为
,
是第三象限内
上一点,,则
的半径长为
A.
B.
C.
D.
二、填空题(共5小题;共25分)
8.
如图,
是
的直径,,
是
上两点,,则
的度数为
?
度.
9.
圆内接四边形
中,,则
?.
10.
如图,
是钝角
的外接圆,连接
.已知
,,则
与
之间的函数表达式为
?.
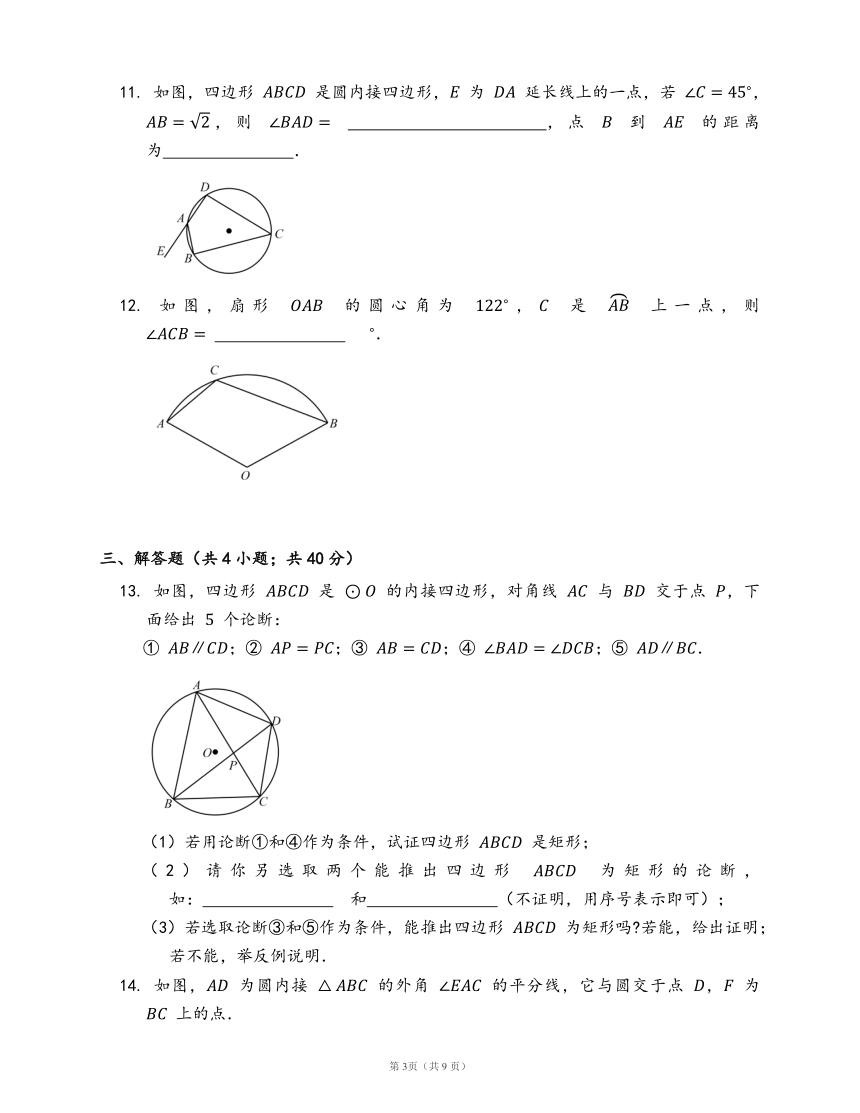
11.
如图,四边形
是圆内接四边形,
为
延长线上的一点,若
,,则
?,点
到
的距离为
?.
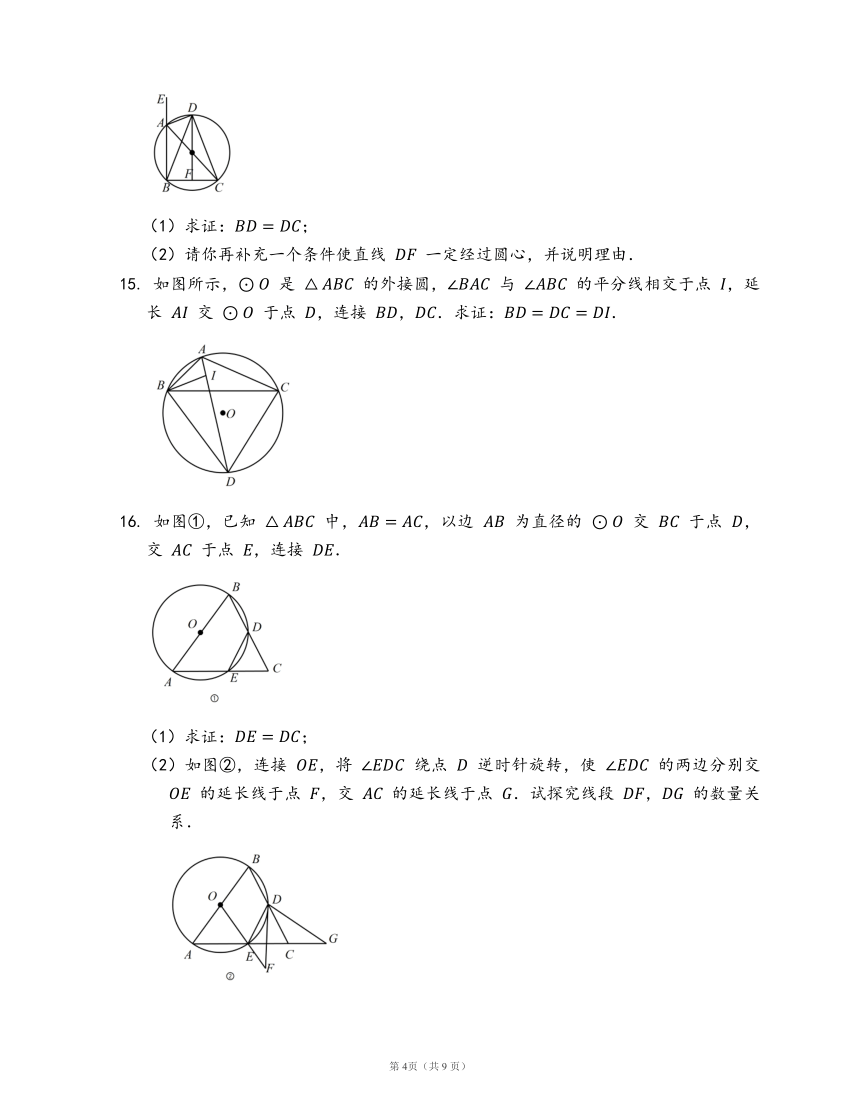
12.
如图,扇形
的圆心角为
,
是
上一点,则
?
.
三、解答题(共4小题;共40分)
13.
如图,四边形
是
的内接四边形,对角线
与
交于点
,下面给出
个论断:
①
;②
;③
;④
;⑤
.
(1)若用论断①和④作为条件,试证四边形
是矩形;
(2)请你另选取两个能推出四边形
为矩形的论断,如:
?
和
?(不证明,用序号表示即可);
(3)若选取论断③和⑤作为条件,能推出四边形
为矩形吗?若能,给出证明;若不能,举反例说明.
14.
如图,
为圆内接
的外角
的平分线,它与圆交于点
,
为
上的点.
(1)求证:;
(2)请你再补充一个条件使直线
一定经过圆心,并说明理由.
15.
如图所示,
是
的外接圆,
与
的平分线相交于点
,延长
交
于点
,连接
,.求证:.
16.
如图①,已知
中,,以边
为直径的
交
于点
,交
于点
,连接
.
(1)求证:;
(2)如图②,连接
,将
绕点
逆时针旋转,使
的两边分别交
的延长线于点
,交
的延长线于点
.试探究线段
,
的数量关系.
答案
第一部分
1.
D
2.
B
3.
A
4.
C
5.
C
6.
C
【解析】
圆周角
与圆心角
所对的弧都是
,
,即
.
四边形
是平行四边形,
,
.
四边形
内接于
,
,即
,
解得
.
7.
C
【解析】
四边形
是圆内接四边形,,
.
,
是
的直径,
.
点
的坐标为
,
,
,
的半径长
.
第二部分
8.
9.
【解析】
四边形
是圆内接四边形,
.
,
设
,则
,,可得
,解得
,
,得
.
10.
【解析】延长
交
于点
,连接
.
为
的直径,
.
为
度数的一半,
为
度数的一半,
为
度数的一半,
,
.
11.
,
【解析】过点
作
于点
,
四边形
为圆内接四边形,,
,
.
又
,
,
.
,
,即点
到
的距离为
.
12.
【解析】提示:连接
.
则
.
,
.
.
第三部分
13.
(1)
四边形
是
的内接四边形,
.
,
.
又
,
,
,
故四边形
是矩形.
??????(2)
①;③(答案不唯一)
??????(3)
不能,例如:如图,
,,四边形
是等腰梯形.
14.
(1)
四边形
是圆内接四边形,
.
又
,
.
是
的平分线,
,
又
,
,
是等腰三角形,
.
??????(2)
答案不唯一,如:
为
的中点,则
经过圆心.理由如下:
由()知
是等腰三角形,
又
为
的中点,
是
的中垂线.
三角形外接圆的圆心是三边中垂线的交点,
必过圆心.
15.
平分
,
,
,
.
平分
,
.
,,
.
,,
,
,
.
16.
(1)
四边形
内接于
,
.
,
.
,
,
,
.
??????(2)
四边形
内接于
,
.
,
.
,
.
,
,
.
,
,即
.
又
,
.
旋转得到
,
,
,即
.
,
,
.
第9页(共9
页)
圆周角2.4.3
圆内接四边形
一、选择题(共7小题;共35分)
1.
已知四边形
内接于圆,则
,,,
的度数之比可能是
A.
B.
C.
D.
2.
下列关于圆内接四边形叙述正确的有
①圆内接四边形的一个外角等于它的内对角;
②圆内接四边形对角相等;
③圆内接四边形中不相邻的两个内角互补;
④在圆内部的四边形叫圆内接四边形.
A.
个
B.
个
C.
个
D.
个
3.
如图,四边形
为
的内接四边形,已知
,则
A.
B.
C.
D.
4.
平行四边形的四个顶点在同一个圆上,则该平行四边形一定是
A.
正方形
B.
菱形
C.
矩形
D.
梯形
5.
如图,点
,,,
都在
上,,,,则
的直径的长是
A.
B.
C.
D.
6.
如图,四边形
内接于
,四边形
是平行四边形,则
A.
B.
C.
D.
7.
如图,
过原点,且与两坐标轴分别交于点
,点
,点
的坐标为
,
是第三象限内
上一点,,则
的半径长为
A.
B.
C.
D.
二、填空题(共5小题;共25分)
8.
如图,
是
的直径,,
是
上两点,,则
的度数为
?
度.
9.
圆内接四边形
中,,则
?.
10.
如图,
是钝角
的外接圆,连接
.已知
,,则
与
之间的函数表达式为
?.
11.
如图,四边形
是圆内接四边形,
为
延长线上的一点,若
,,则
?,点
到
的距离为
?.
12.
如图,扇形
的圆心角为
,
是
上一点,则
?
.
三、解答题(共4小题;共40分)
13.
如图,四边形
是
的内接四边形,对角线
与
交于点
,下面给出
个论断:
①
;②
;③
;④
;⑤
.
(1)若用论断①和④作为条件,试证四边形
是矩形;
(2)请你另选取两个能推出四边形
为矩形的论断,如:
?
和
?(不证明,用序号表示即可);
(3)若选取论断③和⑤作为条件,能推出四边形
为矩形吗?若能,给出证明;若不能,举反例说明.
14.
如图,
为圆内接
的外角
的平分线,它与圆交于点
,
为
上的点.
(1)求证:;
(2)请你再补充一个条件使直线
一定经过圆心,并说明理由.
15.
如图所示,
是
的外接圆,
与
的平分线相交于点
,延长
交
于点
,连接
,.求证:.
16.
如图①,已知
中,,以边
为直径的
交
于点
,交
于点
,连接
.
(1)求证:;
(2)如图②,连接
,将
绕点
逆时针旋转,使
的两边分别交
的延长线于点
,交
的延长线于点
.试探究线段
,
的数量关系.
答案
第一部分
1.
D
2.
B
3.
A
4.
C
5.
C
6.
C
【解析】
圆周角
与圆心角
所对的弧都是
,
,即
.
四边形
是平行四边形,
,
.
四边形
内接于
,
,即
,
解得
.
7.
C
【解析】
四边形
是圆内接四边形,,
.
,
是
的直径,
.
点
的坐标为
,
,
,
的半径长
.
第二部分
8.
9.
【解析】
四边形
是圆内接四边形,
.
,
设
,则
,,可得
,解得
,
,得
.
10.
【解析】延长
交
于点
,连接
.
为
的直径,
.
为
度数的一半,
为
度数的一半,
为
度数的一半,
,
.
11.
,
【解析】过点
作
于点
,
四边形
为圆内接四边形,,
,
.
又
,
,
.
,
,即点
到
的距离为
.
12.
【解析】提示:连接
.
则
.
,
.
.
第三部分
13.
(1)
四边形
是
的内接四边形,
.
,
.
又
,
,
,
故四边形
是矩形.
??????(2)
①;③(答案不唯一)
??????(3)
不能,例如:如图,
,,四边形
是等腰梯形.
14.
(1)
四边形
是圆内接四边形,
.
又
,
.
是
的平分线,
,
又
,
,
是等腰三角形,
.
??????(2)
答案不唯一,如:
为
的中点,则
经过圆心.理由如下:
由()知
是等腰三角形,
又
为
的中点,
是
的中垂线.
三角形外接圆的圆心是三边中垂线的交点,
必过圆心.
15.
平分
,
,
,
.
平分
,
.
,,
.
,,
,
,
.
16.
(1)
四边形
内接于
,
.
,
.
,
,
,
.
??????(2)
四边形
内接于
,
.
,
.
,
.
,
,
.
,
,即
.
又
,
.
旋转得到
,
,
,即
.
,
,
.
第9页(共9
页)
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
