人教版数学九年级下册 26.2实际问题与反比例函数练习题 (word版 含解析)
文档属性
| 名称 | 人教版数学九年级下册 26.2实际问题与反比例函数练习题 (word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 187.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 17:04:41 | ||
图片预览



文档简介
初中数学人教版九年级下册第二十六章26.2实际问题与反比例函数练习题
一、选择题
为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,下列选项错误的是(????)
A. 4月份的利润为50万元
B. 治污改造完成后每月利润比前一个月增加30万元
C. 治污改造完成前后共有4个月的利润低于100万元
D. 9月份该厂利润达到200万元
公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即:阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1200N和0.5m,则动力F(单位:N)关于动力臂l(单位:m)的函数解析式正确的是(????)
A. F=1200l B. F=600l C. F=500l D. F=0.5l
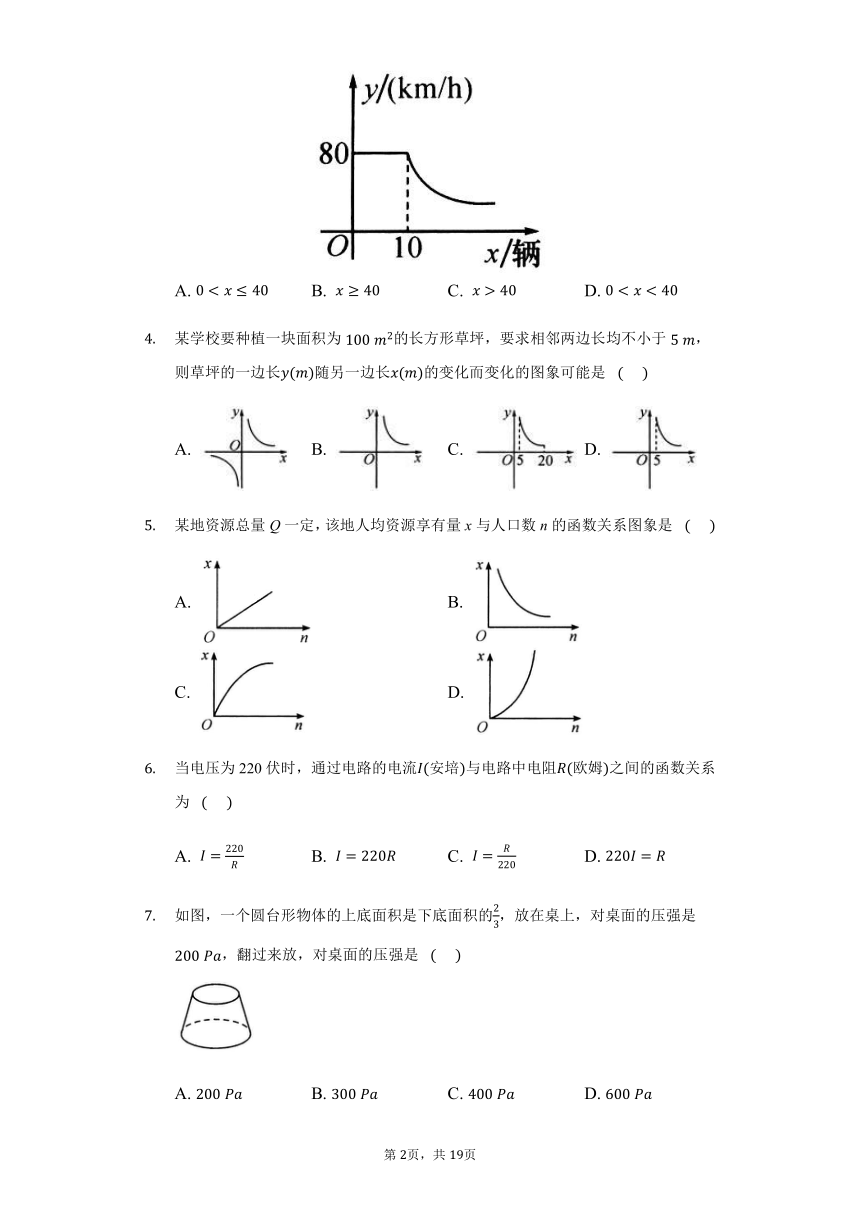
随着私家车的增加,城市的交通也越来越拥挤,通常情况下,某段高架桥上车辆的行驶速度y(km/h)与高架桥上每百米拥有车的数量x(辆)的关系如图所示,当x≥10时,y与x成反比例函数关系,当车辆的行驶速度低于20?km/h,交通就会拥堵.为避免出现交通拥堵,高架桥上每百米拥有车的数量x应该满足的范围是? (??? )
A. 040 D. 0某学校要种植一块面积为100?m2的长方形草坪,要求相邻两边长均不小于5?m,则草坪的一边长y(m)随另一边长x(m)的变化而变化的图象可能是? (??? )
A. B. C. D.
某地资源总量Q一定,该地人均资源享有量x与人口数n的函数关系图象是? (??? )
A. B.
C. D.
当电压为220伏时,通过电路的电流I(安培)与电路中电阻R(欧姆)之间的函数关系为? (??? )
A. I=220R B. I=220R C. I=R220 D. 220I=R
如图,一个圆台形物体的上底面积是下底面积的23,放在桌上,对桌面的压强是200?Pa,翻过来放,对桌面的压强是? (??? )
A. 200?Pa B. 300?Pa C. 400?Pa D. 600?Pa
某人对地面的压强与他和地面接触面积的函数关系如下图所示.若某一沼泽地地面能承受的压强不超过300N/m2,那么此人必须站立在面积________的木板上才不至于下陷.(木板的重量忽略不计)(??? )
A. 至少2m2 B. 至多2m2 C. 大于2m2 D. 小于2m2
已知力F所做的功是15?J(功=力×物体在力的方向上通过的距离),则力F与物体在力的方向上通过的距离s之间的函数关系图象大致是? (??? )
A. B. C. D.
近视眼镜的度数y(度)与镜片焦距x(m)成反比例.已知400度近视眼镜镜片的焦距为0.25m,则y与x之间的函数关系式为
A. y=400x B. y=14x C. y=1100x D. y=100x
如图,点A是反比例函数y=kx图象上的一点,过点A作AC⊥x轴,垂足为C,D为AC的中点,若△AOD的面积为1,则k的值为? (??? )
A. 43 B. 83 C. 3 D. 4
在闭合电路中,电流I,电压U,电阻R之间的关系为:I=UR.电压U(伏特)一定时,电流I(安培)关于电阻R(欧姆)的函数关系的大致图象是(????)
A. B.
C. D.
二、填空题
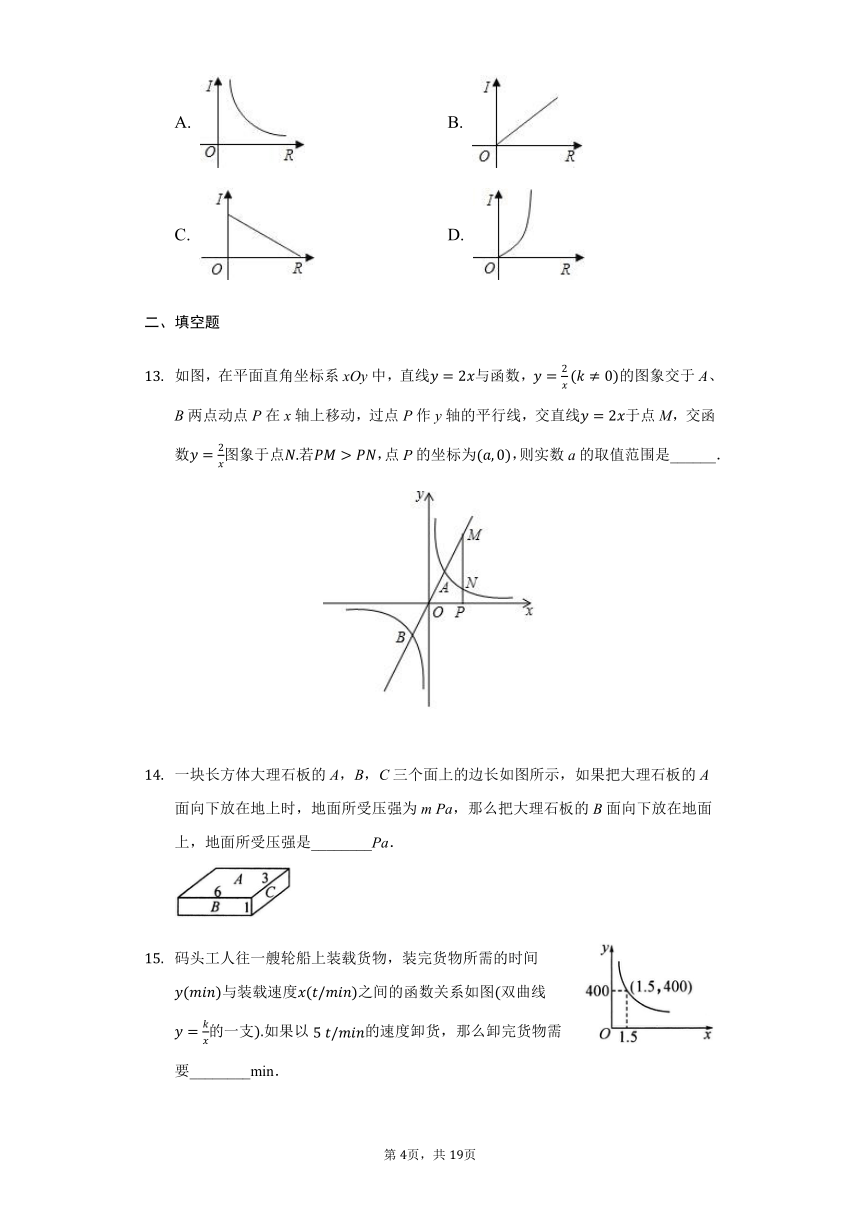
如图,在平面直角坐标系xOy中,直线y=2x与函数,y=2x(k≠0)的图象交于A、B两点动点P在x轴上移动,过点P作y轴的平行线,交直线y=2x于点M,交函数y=2x图象于点N.若PM>PN,点P的坐标为(a,0),则实数a的取值范围是______.
一块长方体大理石板的A,B,C三个面上的边长如图所示,如果把大理石板的A面向下放在地上时,地面所受压强为m Pa,那么把大理石板的B面向下放在地面上,地面所受压强是________Pa.
码头工人往一艘轮船上装载货物,装完货物所需的时间y(min)与装载速度x(t/min)之间的函数关系如图(双曲线y=kx的一支).如果以5?t/min的速度卸货,那么卸完货物需要________min.
某公司汽车司机驾驶汽车将货物从甲地运往乙地,他以60?km/h的平均速度用8?h把货物送到目的地.当他按原路返回时,汽车的速度v(km/h)关于时间t(h)的函数解析式为______________;若公司要求该司机送完货物后必须在6?h内返回公司,则返程时的平均速度不低于________km/h.
某单位要建一个200平方米的矩形草坪,已知它的长是y米,宽是x米,则y与x之间的函数关系式为________,当它的长为25米时,它的宽为________.
三、解答题
如图,电源两端的电压U保持不变,电流强度I与总电阻R成反比例.在实验课上,调整滑动变阻器的电阻,改变灯泡亮度.实验测得电路中总电阻R为15Ω时,通过的电流强度I为0.4A.
(1)求I关于R的函数表达式,并说明比例系数的实际意义;
(2)如果灯泡的电阻为5Ω,电路中电流控制在0.3A到0.6A之间(包括0.3,0.6),那么这个滑动变阻器的电阻应控制在什么范围;
(3)若电路中的总电阻扩大到原来的n倍,则所通过的电流将怎样变化?请利用I关于R的函数表达式来说明理由.
要求取消市场上使用杆秤的呼声越来越高.原因在于一些不法商贩在卖货时将秤砣挖空,或更换较小的秤砣,使秤砣较轻,从而欺骗顾客.
(1)如图,对于同一物体,哪个用了较轻的秤砣?并说明理由.
(2)在称同一物体时,秤砣到支点的距离y与所用秤砣质量x之间满足________关系;
(3)当秤砣较轻时,称得的物体变重,这正好符合哪个函数的哪些性质?
某气球内充满了一定量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)求这一函数的解析式;
(2)当气体体积为1?m3时,气压是多少?
(3)当气球内的气压大于140?kPa时,气球将爆炸,为了安全起见,气体的体积应不小于多少?(精确到0.01?m3)
某学校食堂为方便学生就餐,同时又节约成本,常根据学生的多少来决定开放售饭窗口的数量,假定每个窗口平均每分钟可以售给3个学生,开放10个窗口时,需要1h才能使全部学生就餐完毕.
(1)共有多少学生就餐?
(2)设开放x个窗口时,需要y h才能使就餐的同学全部吃上饭,试求出y与x之间的函数关系.
(3)已知该学校最多可以同时开放20个窗口,那么最少多长时间可以使就餐的学生全部就餐?
答案和解析
1.【答案】C
【解析】解:A、设反比例函数的解析式为y=kx,
把(1,200)代入得,k=200,
∴反比例函数的解析式为:y=200x,
当x=4时,y=50,
∴4月份的利润为50万元,故此选项正确,不合题意;
B、治污改造完成后,从4月到6月,利润从50万到110万,故每月利润比前一个月增加30万元,故此选项正确,不合题意;
C、当y=100时,则100=200x,
解得:x=2,
设一次函数解析式为:y=kx+b,
则4k+b=506k+b=110,
解得:k=30b=?70,
故一次函数解析式为:y=30x?70,
当y=100时,则x=173,
则只有3月,4月,5月,共3个月的利润低于100万元,故此选项不正确,符合题意.
D、一次函数解析式为:y=30x?70,
故y=200时,200=30x?70,
解得:x=9,
则治污改造完成后的第5个月,即9月份该厂利润达到200万元,故此选项正确,不合题意.
故选:C.
直接利用已知点求出一次函数与反比例函数的解析式进而分别分析得出答案.
此题主要考查了一次函数与反比例函数的应用,正确得出函数解析式是解题关键.
2.【答案】B
【解析】解:∵阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1200N和0.5m,
∴动力F(单位:N)关于动力臂l(单位:m)的函数解析式为:1200×0.5=Fl,
则F=600l.
故选:B.
直接利用阻力×阻力臂=动力×动力臂,进而将已知量据代入得出函数关系式.
此题主要考查了反比例函数的应用,正确读懂题意得出关系式是解题关键.
3.【答案】A
【解析】
【分析】
此题主要考查了反比例函数的应用,待定系数法求反比例函数解析式有关知识,利用已知反比例函数图象过(10,80),得出其函数解析式,再利用y=20时,求出x的最值,进而求出x的取值范围.
【解答】
解:设反比例函数的解析式为:y=kx,
则将(10,80),代入得:y=800x,
故当车速度为20千米/时,则20=800x,
解得:x=40,
故高架桥上每百米拥有车的数量x应该满足的范围是:0故选A.
4.【答案】C
【解析】
【分析】
本题主要考查反比例函数的应用,根据反比例函数解析式确定y的取值范围,即可求得x的取值范围,熟练掌握实际问题的反比例函数图象是解题的关键.易知y是x的反比例函数,再根据边长的取值范围即可解题.
【解答】
解:∵草坪面积为100m2,
∴x,y存在关系y=100x,
∵两边长均不小于5m,
∴x≥5,y≥5,
则x≤20,
故选C.
5.【答案】B
【解析】
【分析】
此题考查了反比例函数在实际生活中的应用有关知识,根据题意有:x=Qn;故y与x之间的函数图象是双曲线,且根据x,n的实际意义x,n应大于0;其图象在第一象限.
【解答】
解:∵由题意,得Q=xn,
∴x=Qn,
∵Q为一定值,
∴x是n的反比例函数,其图象为双曲线,
又∵x>0,n>0,
∴图象在第一象限.
故选B.
6.【答案】A
【解析】
【分析】
本题主要考查了根据实际问题列反比例函数关系式,熟知电流I与电阻R成反比例是解题的关键,由物理知识可知,当电压一定时,电流I与电阻R成反比例,即可得出I=UR,再根据U=220伏即可得出函数关系式.
【解答】
解:根据题意设I=UR,
∵U=220伏,
∴I=220R.
故选A.
7.【答案】B
【解析】
【分析】
此题主要考查了反比例函数的应用,根据已知关系式得出F=200S,进而求解是解题关键.利用已知反比例函数解析式,将已知代入求出答案.
【解答】
解:设P=FS,
∵一个圆台形物体正放在桌面上,对桌面的压强是200Pa,
∴P=FS=200,
故F=200S,
∵这个圆台形物体的上底面积是下底面积的23,
则翻过来放,对桌面的压强是:P=200S23S=300(Pa).
故选B.
8.【答案】A
【解析】解:设函数的解析式为P=FS,
∵经过点(10,60)
∴F=PS=10×60=600,
∴P=600S
当P=300时,
S=2,
故选A.
首先根据图象确定反比例函数的解析式,然后代入P=300求得S的值即可.
本题考查了反比例函数的应用,关键是压强公式变形的灵活运用,要知道在水平面上压力等于物体自身的重力,本题所求接触面积为最小面积,接触面积越大,压强越小,越不容易陷入沼泽地.
9.【答案】B
【解析】
【分析】
本题主要考查反比例函数的图象特点:反比例函数y=kx的图象是双曲线,当k>0时,它的两个分支分别位于第一、三象限;当k<0时,它的两个分支分别位于第二、四象限.
先根据题意列出函数关系式,再根据s的取值范围确定其函数图象所在的象限即可.
【解答】
解:已知力F所作的功是15J,
则力F与物体在力的方向上通过的距离S的关系为:F=15s;
且根据实际意义有,s>0;
故其图象只在第一象限.
故选B.
10.【答案】D
【解析】
【分析】
本题考查了根据实际问题列反比例函数关系式,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.反比例函数的一般形式为y=kx(k是常数,且k≠0),常用待定系数法求解函数解析式.设出反比例函数解析式,把(0.25,400)代入即可求解.
【解答】
解:设y=kx,
400度近视眼镜镜片的焦距为0.25m,
即x=0.25,y=400,
∴k=0.25×400=100,
∴y=100x.
故选D.
11.【答案】D
【解析】
【分析】
本题考查了反比例函数的比例系数k的几何意义,三角形的面积有关知识,根据题意可知△AOC的面积为2,然后根据反比例函数系数k的几何意义即可求得k的值.
【解答】
解:∵AC⊥x轴,垂足为点C,D为AC的中点,若△AOD的面积为1,
∴△AOC的面积为2,
∵S△AOC=
1
2
|k|=2,且反比例函数y=
k
x
图象在第一象限,
∴k=4,
故选D.
12.【答案】A
【解析】解:∵I=UR(U>0,R>0)
∴图象是在第一象限的双曲线的一个分支
故选:A.
电阻R之间的关系为:I=UR.电压U(伏特)一定时,电流I(安培)关于电阻R(欧姆)的函数关系为反比例函数其图象为双曲线,电压U>0,电阻R>0,故其图象在第一象限,所以应该选A.
反比例函数y=kx的图象是双曲线,当k>0时,它的两个分支分别位于第一、三象限;当k<0时,它的两个分支分别位于第二、四象限.
13.【答案】a>1或a【解析】解:∵直线y=2x与函数,y=2x(k≠0)的图象交于A、B两点,
∴解y=2xy=2x得x=1y=2或x=?1y=?2,
∴A(1,2),B(?1,?2),
∵动点P在x轴上移动,过点P作y轴的平行线,交直线y=2x于点M,交函数y=2x图象于点N.若PM>PN,
∴a>1或a故答案为a>1或a求得交点A、B的坐标,根据图象即可求得.
本题考查了一次函数与反比例函数的交点问题,利用函数图象性质解决问题是本题的关键.
14.【答案】3m
【解析】
【分析】
本题主要考查反比例函数的应用,待定系数法求反比例函数解析式.由于石板对地面的压力不变,根据题意可求得A面向下时对地面的压力为18m,根据压强公式进而可求得当B面向下时对地面的压强.
【解答】
解:由压强公式可得:p=FS,
当A面向下时对地面的压强为:m=F3×6=F18,
∴F=18m,
当B面向下时对地面的压强为:p=FS=18m6×1=3m.
故答案为3m.
15.【答案】120
【解析】
【分析】此题主要考查了反比例函数的实际应用.解题的关键是根据实际意义列出函数关系式,从实际意义中找到对应的变量的值,利用待定系数法求出函数解析式,再根据题意进行解答.把(1.5,400)代入双曲线y=kx,可求y与x之间的函数关系式;利用函数关系式,当装载速度x=5时,得到y=6005,即可求解.
【解答】
解:把(1.5,400)代入双曲线y=kx,得400=k1.5,解得k=600,
则y与x之间的函数关系式为y=600x.
当x=5时,y=?6005=120.
故答案为120.
16.【答案】ν=480t;80
【解析】
【分析】
本题考查了反比例函数的应用,掌握路程、速度、时间三者之间的关系是解答本题的关键.先根据速度×时间=路程,求出甲地与乙地的路程;再根据行驶速度=路程÷时间,即可得到v与t的函数解析式;由所求的解析式和t≤6可得v的范围.
【解答】
解:由已知得:vt=60×8,
v=480t,
∴t=480t,
∵t≤6,
∴480t≤6,
∴v≥80.
故答案为ν=480t;80.
17.【答案】y=200x(x>0);8
【解析】
【分析】
本题主要考查的是反比例函数解析式的求法和反比例函数的应用的有关知识。由题意利用矩形的面积等于长×宽,即可得到y与x之间的函数解析式,然后将y=25代入解析式即可求解。
【解答】
解:由题意得:
xy=200,
整理得:
y=200x,
当y=25时,25=200x,故x=8
则y与x之间的函数解析式为y=200x,若它的长为25米,则它的宽为8米.
故答案为y=200x;8.
18.【答案】解:(1)由题意得:U=IR,则U=15×0.4=6,则I=6R;
实际意义:电流强度I与总电阻R的乘积是定值,定值为6.
(2)R=6I,当I=0.3时,R=20,当I=0.6时,R=10,
则滑动变阻器的电阻应控制在5?15Ω之间;
(3)总电阻扩大到原来的n倍,由I=6R知,电流缩小到原来的1n.
【解析】(1)由题意得:U=IR,则U=15×0.4=6,即可求解;
(2)R=6I,当I=0.3时,R=20,当I=0.6时,R=10,即可求解;
(3)总电阻扩大到原来的n倍,由I=6R知,即可求解.
本题考查的是反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后根据关系式求解相关数据.
19.【答案】解:(1)图①用了较轻的秤砣.
理由如下:设重物的质量为G,秤砣的质量为x,重物的受力点到支点的距离为l.
∵G,l为定值,xy=Gl,且y1>y2,
∴x1故图①中的秤砣较轻;
(2)反比例函数;
(3)符合反比例函数y=Glx(x>0)“在第一象限内,y随x的增大而减小”的性质.
【解析】解:(1)见答案;
(2)由(1)可知称得的物体变重,说明秤砣到提纽之间的距离变大,秤砣越轻,秤砣到提纽之间的距离就会越大,物体就会变得越重,但实际物体质量与物体到提纽之间的距离的乘积不变,因此所称得的物体质量与所用秤砣质量之间满足反比例函数关系;
故答案为:反比例函数.
(3)见答案.
(1)利用杠杆的原理来解决,物体质量×物体到提纽之间的距离=秤砣质量×秤砣到提纽之间的距离,由图可知答案;
(2)由(1)可知物体到提纽之间的距离是一定的,所称得的物体质量与所用秤砣质量之间满足反比例关系;
(3)当物体质量与物体到提纽之间的距离的乘积不变时,当砣较轻时,秤砣到提纽之间的距离变大,显示物体变重,由此得出函数的性质.
此题是运用(杠杆的原理)反比例函数的观点来解决实际问题.从实际意义中找到对应的变量的值,利用待定系数法求出函数解析式.会用不等式解决实际问题.
20.【答案】解:(1)设p=kV,由题意知120=k0.8,所以k=96,故p=96V.
(2)当V=1?m3时,p=961=96(kPa).
所以当气体体积为1?m3时,气压是96?kPa.
(3)当p=140?kPa时,V=96140≈0.69(m3).
所以为了安全起见,气体的体积应不少于0.69?m3.
【解析】考查反比例函数的应用;应熟练掌握符合反比例函数解析式的数值的意义.
(1)设出反比例函数解析式,把A坐标代入可得函数解析式;
(2)把V=1代入(1)得到的函数解析式,可得p;
(3)把p=140代入得到V即可.
21.【答案】解:(1)3×10×60=1800;?
答:共有1800学生就餐.
(2)依题意得3×60xy=1800,
∴y=10x;?
(3)当x=20时,
y=1020=12小时=30分钟,
故最少30分钟可以使就餐学生全部就餐.
【解析】本题考查的是有理数的混合运算,反比例函数应用有关知识.
(1)根据题意列出算式进行即可解答;
(2)设开放x个窗口,找出数量关系列出函数关系即可;
(3)把x=20代入函数解析式中即可解答.
一、选择题
为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,下列选项错误的是(????)
A. 4月份的利润为50万元
B. 治污改造完成后每月利润比前一个月增加30万元
C. 治污改造完成前后共有4个月的利润低于100万元
D. 9月份该厂利润达到200万元
公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即:阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1200N和0.5m,则动力F(单位:N)关于动力臂l(单位:m)的函数解析式正确的是(????)
A. F=1200l B. F=600l C. F=500l D. F=0.5l
随着私家车的增加,城市的交通也越来越拥挤,通常情况下,某段高架桥上车辆的行驶速度y(km/h)与高架桥上每百米拥有车的数量x(辆)的关系如图所示,当x≥10时,y与x成反比例函数关系,当车辆的行驶速度低于20?km/h,交通就会拥堵.为避免出现交通拥堵,高架桥上每百米拥有车的数量x应该满足的范围是? (??? )
A. 0
A. B. C. D.
某地资源总量Q一定,该地人均资源享有量x与人口数n的函数关系图象是? (??? )
A. B.
C. D.
当电压为220伏时,通过电路的电流I(安培)与电路中电阻R(欧姆)之间的函数关系为? (??? )
A. I=220R B. I=220R C. I=R220 D. 220I=R
如图,一个圆台形物体的上底面积是下底面积的23,放在桌上,对桌面的压强是200?Pa,翻过来放,对桌面的压强是? (??? )
A. 200?Pa B. 300?Pa C. 400?Pa D. 600?Pa
某人对地面的压强与他和地面接触面积的函数关系如下图所示.若某一沼泽地地面能承受的压强不超过300N/m2,那么此人必须站立在面积________的木板上才不至于下陷.(木板的重量忽略不计)(??? )
A. 至少2m2 B. 至多2m2 C. 大于2m2 D. 小于2m2
已知力F所做的功是15?J(功=力×物体在力的方向上通过的距离),则力F与物体在力的方向上通过的距离s之间的函数关系图象大致是? (??? )
A. B. C. D.
近视眼镜的度数y(度)与镜片焦距x(m)成反比例.已知400度近视眼镜镜片的焦距为0.25m,则y与x之间的函数关系式为
A. y=400x B. y=14x C. y=1100x D. y=100x
如图,点A是反比例函数y=kx图象上的一点,过点A作AC⊥x轴,垂足为C,D为AC的中点,若△AOD的面积为1,则k的值为? (??? )
A. 43 B. 83 C. 3 D. 4
在闭合电路中,电流I,电压U,电阻R之间的关系为:I=UR.电压U(伏特)一定时,电流I(安培)关于电阻R(欧姆)的函数关系的大致图象是(????)
A. B.
C. D.
二、填空题
如图,在平面直角坐标系xOy中,直线y=2x与函数,y=2x(k≠0)的图象交于A、B两点动点P在x轴上移动,过点P作y轴的平行线,交直线y=2x于点M,交函数y=2x图象于点N.若PM>PN,点P的坐标为(a,0),则实数a的取值范围是______.
一块长方体大理石板的A,B,C三个面上的边长如图所示,如果把大理石板的A面向下放在地上时,地面所受压强为m Pa,那么把大理石板的B面向下放在地面上,地面所受压强是________Pa.
码头工人往一艘轮船上装载货物,装完货物所需的时间y(min)与装载速度x(t/min)之间的函数关系如图(双曲线y=kx的一支).如果以5?t/min的速度卸货,那么卸完货物需要________min.
某公司汽车司机驾驶汽车将货物从甲地运往乙地,他以60?km/h的平均速度用8?h把货物送到目的地.当他按原路返回时,汽车的速度v(km/h)关于时间t(h)的函数解析式为______________;若公司要求该司机送完货物后必须在6?h内返回公司,则返程时的平均速度不低于________km/h.
某单位要建一个200平方米的矩形草坪,已知它的长是y米,宽是x米,则y与x之间的函数关系式为________,当它的长为25米时,它的宽为________.
三、解答题
如图,电源两端的电压U保持不变,电流强度I与总电阻R成反比例.在实验课上,调整滑动变阻器的电阻,改变灯泡亮度.实验测得电路中总电阻R为15Ω时,通过的电流强度I为0.4A.
(1)求I关于R的函数表达式,并说明比例系数的实际意义;
(2)如果灯泡的电阻为5Ω,电路中电流控制在0.3A到0.6A之间(包括0.3,0.6),那么这个滑动变阻器的电阻应控制在什么范围;
(3)若电路中的总电阻扩大到原来的n倍,则所通过的电流将怎样变化?请利用I关于R的函数表达式来说明理由.
要求取消市场上使用杆秤的呼声越来越高.原因在于一些不法商贩在卖货时将秤砣挖空,或更换较小的秤砣,使秤砣较轻,从而欺骗顾客.
(1)如图,对于同一物体,哪个用了较轻的秤砣?并说明理由.
(2)在称同一物体时,秤砣到支点的距离y与所用秤砣质量x之间满足________关系;
(3)当秤砣较轻时,称得的物体变重,这正好符合哪个函数的哪些性质?
某气球内充满了一定量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)求这一函数的解析式;
(2)当气体体积为1?m3时,气压是多少?
(3)当气球内的气压大于140?kPa时,气球将爆炸,为了安全起见,气体的体积应不小于多少?(精确到0.01?m3)
某学校食堂为方便学生就餐,同时又节约成本,常根据学生的多少来决定开放售饭窗口的数量,假定每个窗口平均每分钟可以售给3个学生,开放10个窗口时,需要1h才能使全部学生就餐完毕.
(1)共有多少学生就餐?
(2)设开放x个窗口时,需要y h才能使就餐的同学全部吃上饭,试求出y与x之间的函数关系.
(3)已知该学校最多可以同时开放20个窗口,那么最少多长时间可以使就餐的学生全部就餐?
答案和解析
1.【答案】C
【解析】解:A、设反比例函数的解析式为y=kx,
把(1,200)代入得,k=200,
∴反比例函数的解析式为:y=200x,
当x=4时,y=50,
∴4月份的利润为50万元,故此选项正确,不合题意;
B、治污改造完成后,从4月到6月,利润从50万到110万,故每月利润比前一个月增加30万元,故此选项正确,不合题意;
C、当y=100时,则100=200x,
解得:x=2,
设一次函数解析式为:y=kx+b,
则4k+b=506k+b=110,
解得:k=30b=?70,
故一次函数解析式为:y=30x?70,
当y=100时,则x=173,
则只有3月,4月,5月,共3个月的利润低于100万元,故此选项不正确,符合题意.
D、一次函数解析式为:y=30x?70,
故y=200时,200=30x?70,
解得:x=9,
则治污改造完成后的第5个月,即9月份该厂利润达到200万元,故此选项正确,不合题意.
故选:C.
直接利用已知点求出一次函数与反比例函数的解析式进而分别分析得出答案.
此题主要考查了一次函数与反比例函数的应用,正确得出函数解析式是解题关键.
2.【答案】B
【解析】解:∵阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1200N和0.5m,
∴动力F(单位:N)关于动力臂l(单位:m)的函数解析式为:1200×0.5=Fl,
则F=600l.
故选:B.
直接利用阻力×阻力臂=动力×动力臂,进而将已知量据代入得出函数关系式.
此题主要考查了反比例函数的应用,正确读懂题意得出关系式是解题关键.
3.【答案】A
【解析】
【分析】
此题主要考查了反比例函数的应用,待定系数法求反比例函数解析式有关知识,利用已知反比例函数图象过(10,80),得出其函数解析式,再利用y=20时,求出x的最值,进而求出x的取值范围.
【解答】
解:设反比例函数的解析式为:y=kx,
则将(10,80),代入得:y=800x,
故当车速度为20千米/时,则20=800x,
解得:x=40,
故高架桥上每百米拥有车的数量x应该满足的范围是:0
4.【答案】C
【解析】
【分析】
本题主要考查反比例函数的应用,根据反比例函数解析式确定y的取值范围,即可求得x的取值范围,熟练掌握实际问题的反比例函数图象是解题的关键.易知y是x的反比例函数,再根据边长的取值范围即可解题.
【解答】
解:∵草坪面积为100m2,
∴x,y存在关系y=100x,
∵两边长均不小于5m,
∴x≥5,y≥5,
则x≤20,
故选C.
5.【答案】B
【解析】
【分析】
此题考查了反比例函数在实际生活中的应用有关知识,根据题意有:x=Qn;故y与x之间的函数图象是双曲线,且根据x,n的实际意义x,n应大于0;其图象在第一象限.
【解答】
解:∵由题意,得Q=xn,
∴x=Qn,
∵Q为一定值,
∴x是n的反比例函数,其图象为双曲线,
又∵x>0,n>0,
∴图象在第一象限.
故选B.
6.【答案】A
【解析】
【分析】
本题主要考查了根据实际问题列反比例函数关系式,熟知电流I与电阻R成反比例是解题的关键,由物理知识可知,当电压一定时,电流I与电阻R成反比例,即可得出I=UR,再根据U=220伏即可得出函数关系式.
【解答】
解:根据题意设I=UR,
∵U=220伏,
∴I=220R.
故选A.
7.【答案】B
【解析】
【分析】
此题主要考查了反比例函数的应用,根据已知关系式得出F=200S,进而求解是解题关键.利用已知反比例函数解析式,将已知代入求出答案.
【解答】
解:设P=FS,
∵一个圆台形物体正放在桌面上,对桌面的压强是200Pa,
∴P=FS=200,
故F=200S,
∵这个圆台形物体的上底面积是下底面积的23,
则翻过来放,对桌面的压强是:P=200S23S=300(Pa).
故选B.
8.【答案】A
【解析】解:设函数的解析式为P=FS,
∵经过点(10,60)
∴F=PS=10×60=600,
∴P=600S
当P=300时,
S=2,
故选A.
首先根据图象确定反比例函数的解析式,然后代入P=300求得S的值即可.
本题考查了反比例函数的应用,关键是压强公式变形的灵活运用,要知道在水平面上压力等于物体自身的重力,本题所求接触面积为最小面积,接触面积越大,压强越小,越不容易陷入沼泽地.
9.【答案】B
【解析】
【分析】
本题主要考查反比例函数的图象特点:反比例函数y=kx的图象是双曲线,当k>0时,它的两个分支分别位于第一、三象限;当k<0时,它的两个分支分别位于第二、四象限.
先根据题意列出函数关系式,再根据s的取值范围确定其函数图象所在的象限即可.
【解答】
解:已知力F所作的功是15J,
则力F与物体在力的方向上通过的距离S的关系为:F=15s;
且根据实际意义有,s>0;
故其图象只在第一象限.
故选B.
10.【答案】D
【解析】
【分析】
本题考查了根据实际问题列反比例函数关系式,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.反比例函数的一般形式为y=kx(k是常数,且k≠0),常用待定系数法求解函数解析式.设出反比例函数解析式,把(0.25,400)代入即可求解.
【解答】
解:设y=kx,
400度近视眼镜镜片的焦距为0.25m,
即x=0.25,y=400,
∴k=0.25×400=100,
∴y=100x.
故选D.
11.【答案】D
【解析】
【分析】
本题考查了反比例函数的比例系数k的几何意义,三角形的面积有关知识,根据题意可知△AOC的面积为2,然后根据反比例函数系数k的几何意义即可求得k的值.
【解答】
解:∵AC⊥x轴,垂足为点C,D为AC的中点,若△AOD的面积为1,
∴△AOC的面积为2,
∵S△AOC=
1
2
|k|=2,且反比例函数y=
k
x
图象在第一象限,
∴k=4,
故选D.
12.【答案】A
【解析】解:∵I=UR(U>0,R>0)
∴图象是在第一象限的双曲线的一个分支
故选:A.
电阻R之间的关系为:I=UR.电压U(伏特)一定时,电流I(安培)关于电阻R(欧姆)的函数关系为反比例函数其图象为双曲线,电压U>0,电阻R>0,故其图象在第一象限,所以应该选A.
反比例函数y=kx的图象是双曲线,当k>0时,它的两个分支分别位于第一、三象限;当k<0时,它的两个分支分别位于第二、四象限.
13.【答案】a>1或a【解析】解:∵直线y=2x与函数,y=2x(k≠0)的图象交于A、B两点,
∴解y=2xy=2x得x=1y=2或x=?1y=?2,
∴A(1,2),B(?1,?2),
∵动点P在x轴上移动,过点P作y轴的平行线,交直线y=2x于点M,交函数y=2x图象于点N.若PM>PN,
∴a>1或a故答案为a>1或a求得交点A、B的坐标,根据图象即可求得.
本题考查了一次函数与反比例函数的交点问题,利用函数图象性质解决问题是本题的关键.
14.【答案】3m
【解析】
【分析】
本题主要考查反比例函数的应用,待定系数法求反比例函数解析式.由于石板对地面的压力不变,根据题意可求得A面向下时对地面的压力为18m,根据压强公式进而可求得当B面向下时对地面的压强.
【解答】
解:由压强公式可得:p=FS,
当A面向下时对地面的压强为:m=F3×6=F18,
∴F=18m,
当B面向下时对地面的压强为:p=FS=18m6×1=3m.
故答案为3m.
15.【答案】120
【解析】
【分析】此题主要考查了反比例函数的实际应用.解题的关键是根据实际意义列出函数关系式,从实际意义中找到对应的变量的值,利用待定系数法求出函数解析式,再根据题意进行解答.把(1.5,400)代入双曲线y=kx,可求y与x之间的函数关系式;利用函数关系式,当装载速度x=5时,得到y=6005,即可求解.
【解答】
解:把(1.5,400)代入双曲线y=kx,得400=k1.5,解得k=600,
则y与x之间的函数关系式为y=600x.
当x=5时,y=?6005=120.
故答案为120.
16.【答案】ν=480t;80
【解析】
【分析】
本题考查了反比例函数的应用,掌握路程、速度、时间三者之间的关系是解答本题的关键.先根据速度×时间=路程,求出甲地与乙地的路程;再根据行驶速度=路程÷时间,即可得到v与t的函数解析式;由所求的解析式和t≤6可得v的范围.
【解答】
解:由已知得:vt=60×8,
v=480t,
∴t=480t,
∵t≤6,
∴480t≤6,
∴v≥80.
故答案为ν=480t;80.
17.【答案】y=200x(x>0);8
【解析】
【分析】
本题主要考查的是反比例函数解析式的求法和反比例函数的应用的有关知识。由题意利用矩形的面积等于长×宽,即可得到y与x之间的函数解析式,然后将y=25代入解析式即可求解。
【解答】
解:由题意得:
xy=200,
整理得:
y=200x,
当y=25时,25=200x,故x=8
则y与x之间的函数解析式为y=200x,若它的长为25米,则它的宽为8米.
故答案为y=200x;8.
18.【答案】解:(1)由题意得:U=IR,则U=15×0.4=6,则I=6R;
实际意义:电流强度I与总电阻R的乘积是定值,定值为6.
(2)R=6I,当I=0.3时,R=20,当I=0.6时,R=10,
则滑动变阻器的电阻应控制在5?15Ω之间;
(3)总电阻扩大到原来的n倍,由I=6R知,电流缩小到原来的1n.
【解析】(1)由题意得:U=IR,则U=15×0.4=6,即可求解;
(2)R=6I,当I=0.3时,R=20,当I=0.6时,R=10,即可求解;
(3)总电阻扩大到原来的n倍,由I=6R知,即可求解.
本题考查的是反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后根据关系式求解相关数据.
19.【答案】解:(1)图①用了较轻的秤砣.
理由如下:设重物的质量为G,秤砣的质量为x,重物的受力点到支点的距离为l.
∵G,l为定值,xy=Gl,且y1>y2,
∴x1
(2)反比例函数;
(3)符合反比例函数y=Glx(x>0)“在第一象限内,y随x的增大而减小”的性质.
【解析】解:(1)见答案;
(2)由(1)可知称得的物体变重,说明秤砣到提纽之间的距离变大,秤砣越轻,秤砣到提纽之间的距离就会越大,物体就会变得越重,但实际物体质量与物体到提纽之间的距离的乘积不变,因此所称得的物体质量与所用秤砣质量之间满足反比例函数关系;
故答案为:反比例函数.
(3)见答案.
(1)利用杠杆的原理来解决,物体质量×物体到提纽之间的距离=秤砣质量×秤砣到提纽之间的距离,由图可知答案;
(2)由(1)可知物体到提纽之间的距离是一定的,所称得的物体质量与所用秤砣质量之间满足反比例关系;
(3)当物体质量与物体到提纽之间的距离的乘积不变时,当砣较轻时,秤砣到提纽之间的距离变大,显示物体变重,由此得出函数的性质.
此题是运用(杠杆的原理)反比例函数的观点来解决实际问题.从实际意义中找到对应的变量的值,利用待定系数法求出函数解析式.会用不等式解决实际问题.
20.【答案】解:(1)设p=kV,由题意知120=k0.8,所以k=96,故p=96V.
(2)当V=1?m3时,p=961=96(kPa).
所以当气体体积为1?m3时,气压是96?kPa.
(3)当p=140?kPa时,V=96140≈0.69(m3).
所以为了安全起见,气体的体积应不少于0.69?m3.
【解析】考查反比例函数的应用;应熟练掌握符合反比例函数解析式的数值的意义.
(1)设出反比例函数解析式,把A坐标代入可得函数解析式;
(2)把V=1代入(1)得到的函数解析式,可得p;
(3)把p=140代入得到V即可.
21.【答案】解:(1)3×10×60=1800;?
答:共有1800学生就餐.
(2)依题意得3×60xy=1800,
∴y=10x;?
(3)当x=20时,
y=1020=12小时=30分钟,
故最少30分钟可以使就餐学生全部就餐.
【解析】本题考查的是有理数的混合运算,反比例函数应用有关知识.
(1)根据题意列出算式进行即可解答;
(2)设开放x个窗口,找出数量关系列出函数关系即可;
(3)把x=20代入函数解析式中即可解答.
