广西柳江中学2020-2021学年高一上学期数学周测试卷(12月9日) Word版含答案
文档属性
| 名称 | 广西柳江中学2020-2021学年高一上学期数学周测试卷(12月9日) Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 131.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 07:47:48 | ||
图片预览



文档简介
柳江中学2020年12月9日高一数学周测
一.选择题(共12小题)
1.已知集合U=R,A={x|x=2n,n∈N},B={x|x(x﹣2)>0},则A∩(?UB)=( )
A.{0} B.{2} C.{0,2} D.{0,1,2}
2.设a=30.5,b=log0.53,c=0.53.则a,b,c的大小关系为( )
A.a>b>c B.c>b>a C.a>c>b D.c>a>b
3.已知x?log32=1,则4x=( )
A.4 B.6 C.4 D.9
4.若幂函数f(x)的图象过点(4,2),则f(a2)=( )
A.a B.﹣a C.±a D.|a|
41167053378205.图中C1、C2、C3为三个幂函数y=xα在第一象限内的图象,则解析式中指数α的值依次可以是( )
A.、3、﹣1 B.﹣1、3、
C.、﹣1、3 D.﹣1、、3
6.方程lgx+2x=3的解所在区间为( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
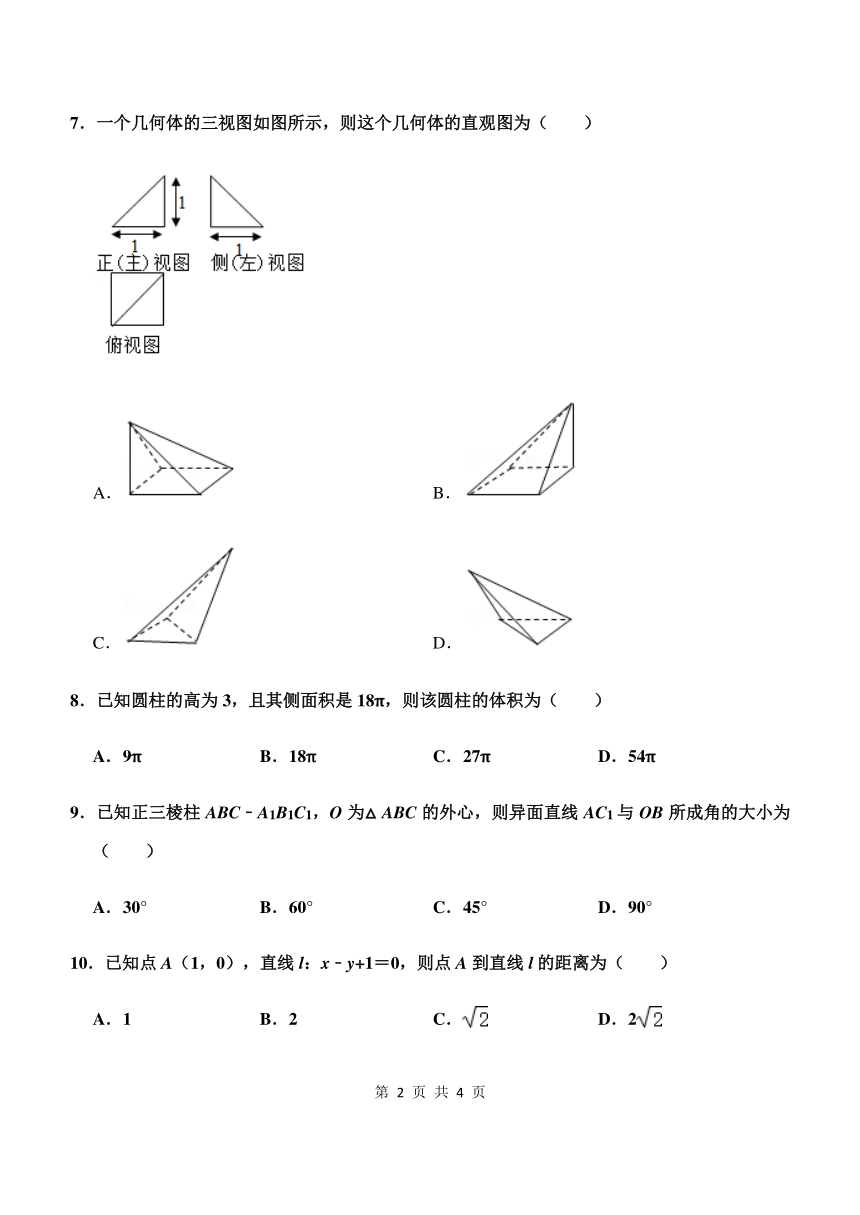
7.一个几何体的三视图如图所示,则这个几何体的直观图为( )
A. B.
C. D.
8.已知圆柱的高为3,且其侧面积是18π,则该圆柱的体积为( )
A.9π B.18π C.27π D.54π
9.已知正三棱柱ABC﹣A1B1C1,O为△ABC的外心,则异面直线AC1与OB所成角的大小为( )
A.30° B.60° C.45° D.90°
10.已知点A(1,0),直线l:x﹣y+1=0,则点A到直线l的距离为( )
A.1 B.2 C. D.2
11.已知直线x+2y+3=0与直线2x+my+1=0平行,则它们之间的距离为( )
A. B. C. D.
12.若函数f(x)=x2+(a﹣2)x+1为偶函数,g(x)=为奇函数,则a+b的值为( )
A.2 B.3 C.4 D.5
二.填空题(共4小题)
13.函数f(x)=ax﹣2019+2019(a>0且a≠1)图象所过的定点坐标是
14.直线l1:ax+3y+1=0,与l2:2x+(a+1)y+1=0.若l1∥l2,则实数a= ;若l1⊥l2,则实数a= .
15.已知直线l经过两条直线2x﹣3y+10=0和3x+4y﹣2=0的交点,且垂直于直线3x﹣2y+4=0,则直线l方程为 .
16.已知平面α,β,γ和直线a,b,则下列命题正确的是 (填序号).
①若α⊥β,β⊥γ,则α∥γ; ②若α∥β,β⊥γ,则α⊥γ;
③若α∩β=a,β∩γ=b,α⊥β,则a⊥b; ④若α⊥β,α∩β=a,a⊥b,则b⊥α;
⑤若a⊥α,a∥β,则α⊥β.
三.解答题(共8小题)
17.已知函数f(x)=x|x|﹣2x,x∈R.
(1)求y=f(x)的奇偶性;
(2)画出函数y=f(x)的图象;
(3)求y=f(x),x∈[﹣4,2]的值域.
18.已知二次函数f(x)=ax2+bx+c,满足f(1+x)=f(1﹣x)且不等式f(x)≤2x的解集为[1,3].
(1)求函数f(x)的解析式;
(2)方程f(x)=2x+k在(0,3]上有解,求实数k的取值范围.
19.设函数f(x)=loga(3+x)+loga(3﹣x),(a>0,且a≠1),f(1)=3.
(1)求a的值及f(x)的定义域;
(2)判断f(x)的奇偶性,并给出证明;
(3)求函数f(x)在[1,2]上的值域.
20.直线l过点(1,4),且倾斜角为45°.
(1)求直线l的方程;
(2)求直线l与坐标轴所围成的三角形面积.
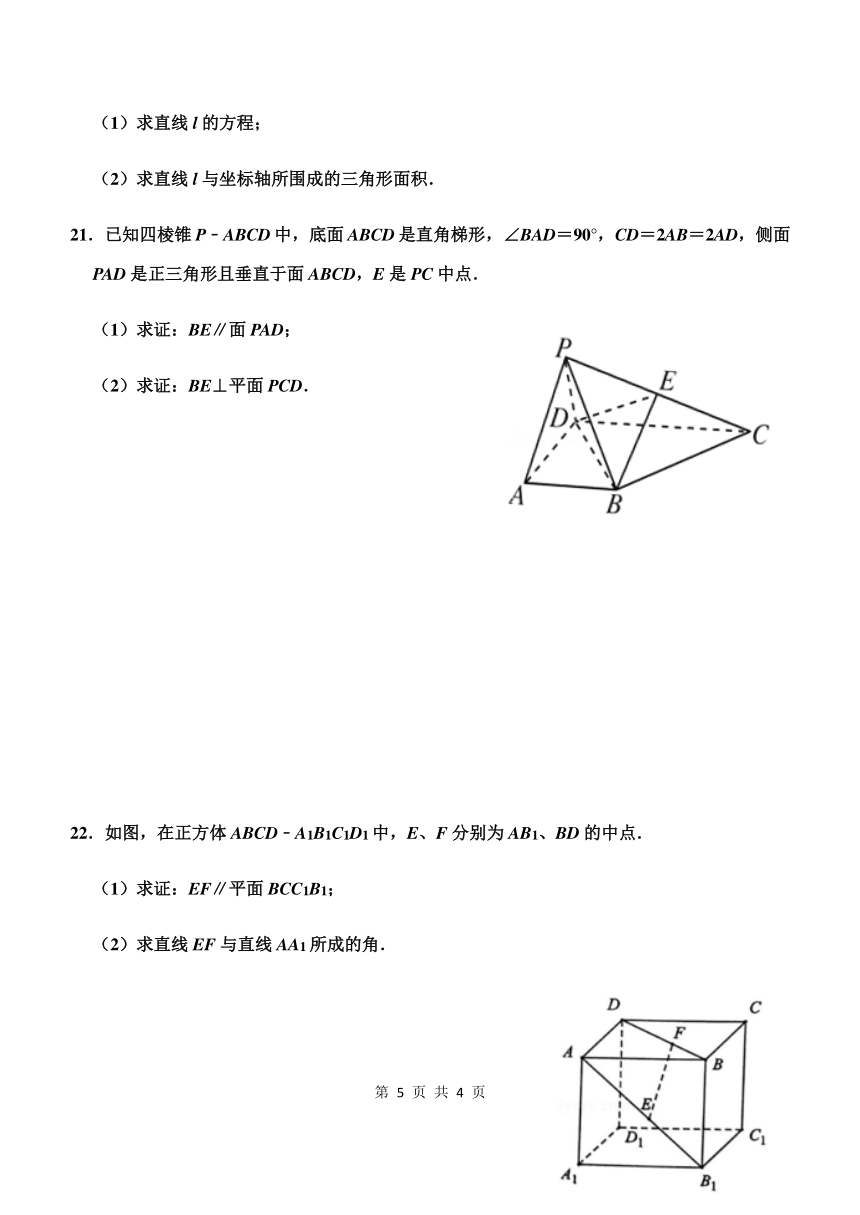
21.已知四棱锥P﹣ABCD中,底面ABCD是直角梯形,∠BAD=90°,CD=2AB=2AD,侧面PAD是正三角形且垂直于面ABCD,E是PC中点.
3364230198120(1)求证:BE∥面PAD;
(2)求证:BE⊥平面PCD.
22.如图,在正方体ABCD﹣A1B1C1D1中,E、F分别为AB1、BD的中点.
(1)求证:EF∥平面BCC1B1;
(2)求直线EF与直线AA1所成的角.
3735705135890
2020年12月9日数学周测
参考答案与试题解析
一.选择题(共20小题)
1.C 2 C 3 D 4 D 5D 6B 7B 8C 9D 10C 11A 12D
二.填空题(共4小题)
13(2019,2020)
14.﹣3;﹣
15.2x+3y﹣2=0.
16.②⑤.
三.解答题(共6小题)
17.
【解答】解:(1)函数的定义域为R,
∵f(﹣x)=﹣x|﹣x|﹣2(﹣x)=﹣x|x|+2x=﹣(x|x|﹣2x)=﹣f(x),
∴f(x)为奇函数,
(2)f(x)=x|x|﹣2x=,
图象如图所示:
(3)由f(﹣4)=﹣4×|4|﹣2×(﹣4)=﹣16+8=﹣8,f(2)=2×|2|﹣2×2=0,f(﹣1)=﹣1×|﹣1|﹣2×(﹣1)=1,
结合图象可得y=f(x),x∈[﹣4,2]的值域为[﹣8,1].
18.
【解答】解:(1)由f(1+x)=f(1﹣x)知:f(x)关于x=1对称,
故﹣=1,即b=﹣2a,
又f(x)≤2x的解集是[1,3],
即ax2﹣(2a+2)x+c=0的两根是1,3,
即,解得:,
故f(x)=x2﹣2x+3;
(2)方程f(x)=2x+k在(0,3]上有解,
即方程k=x2﹣4x+3在(0,3]上有解,
即y=k的图象和g(x)=x2﹣4x+3的图象在(0,3]上有交点,
g(x)=(x﹣2)2﹣1,对称轴是x=2,
故g(x)在(0,2)递减,在(2,3]递增,
g(0)=3,g(2)=﹣1,故x∈(0,3]时,g(x)∈[﹣1,3),
故﹣1≤k<3.
19.
【解答】解:(1)因为f(x)=loga(3+x)+loga(3﹣x)=,
由题意f(1)=loga8=3,
故a=2,
由可得﹣3<x<3,
故函数的定义域(﹣3,3);
(2)因为f(﹣x)=loga(9﹣x2)=f(x),即函数f(x)为偶函数,
(3)∵1≤x≤2,
所以5≤9﹣x2≤8,
当a=2>1时,函数的值域[loga5,loga8],
20.
【解答】解:(1)∵直线l过点(1,4),且倾斜角为45°,故它的斜率为tan45°=1,
故它的方程为 y﹣4=1×(x﹣1),即x﹣y+3=0.
(2)∵直线x﹣y+3=0和坐标轴的交点为(﹣3,0)、(0,3),
故它与坐标轴所围成的三角形面积为×3×3=.
21.
【解答】证明:(1)取PD的中点F,连接AF、EF,
∵E是PC中点,∴EF∥CD,EF=CD,
∵AB∥CD,CD=2AB,
∴EF∥AB,EF=AB,
∴四边形ABEF是平行四边形,
∴BE∥AF,
又BE?平面PAD,AF?平面PAD,
∴BE∥面PAD.
(2)∵面PAD⊥面ABCD,面PAD∩面ABCD=AD,CD⊥AD,
∴CD⊥面PAD,
∵AF?平面PAD,∴CD⊥AF,
∵等边三角形PAD,F为PD的中点,∴AF⊥PD,
又CD∩PD=D,CD、PD?平面PCD,∴AF⊥平面PCD,
∵AF∥BE,∴BE⊥平面PCD.
22.如图,D
【解答】解:(1)证明:连结AC,B1C,
∵F是正方形ABCD对角线BC的中点,
∴F是AC的中点,
∵E是AB1的中点,∴EF∥B1C,
又EF?平面BCC1B1,B1C?面BCC1B1,
∴EF∥平面BCC1B1.
(2)由(1)知EF∥B1C,且AA1∥BB1,
∴直线EF与直线AA1所成角为直线B1C与直线BB1所成角,
∵正方形BCC1B1中,∠BB1C=45°,
∴直线EF与直线AA1所成的角为45°.
3049905102870
一.选择题(共12小题)
1.已知集合U=R,A={x|x=2n,n∈N},B={x|x(x﹣2)>0},则A∩(?UB)=( )
A.{0} B.{2} C.{0,2} D.{0,1,2}
2.设a=30.5,b=log0.53,c=0.53.则a,b,c的大小关系为( )
A.a>b>c B.c>b>a C.a>c>b D.c>a>b
3.已知x?log32=1,则4x=( )
A.4 B.6 C.4 D.9
4.若幂函数f(x)的图象过点(4,2),则f(a2)=( )
A.a B.﹣a C.±a D.|a|
41167053378205.图中C1、C2、C3为三个幂函数y=xα在第一象限内的图象,则解析式中指数α的值依次可以是( )
A.、3、﹣1 B.﹣1、3、
C.、﹣1、3 D.﹣1、、3
6.方程lgx+2x=3的解所在区间为( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
7.一个几何体的三视图如图所示,则这个几何体的直观图为( )
A. B.
C. D.
8.已知圆柱的高为3,且其侧面积是18π,则该圆柱的体积为( )
A.9π B.18π C.27π D.54π
9.已知正三棱柱ABC﹣A1B1C1,O为△ABC的外心,则异面直线AC1与OB所成角的大小为( )
A.30° B.60° C.45° D.90°
10.已知点A(1,0),直线l:x﹣y+1=0,则点A到直线l的距离为( )
A.1 B.2 C. D.2
11.已知直线x+2y+3=0与直线2x+my+1=0平行,则它们之间的距离为( )
A. B. C. D.
12.若函数f(x)=x2+(a﹣2)x+1为偶函数,g(x)=为奇函数,则a+b的值为( )
A.2 B.3 C.4 D.5
二.填空题(共4小题)
13.函数f(x)=ax﹣2019+2019(a>0且a≠1)图象所过的定点坐标是
14.直线l1:ax+3y+1=0,与l2:2x+(a+1)y+1=0.若l1∥l2,则实数a= ;若l1⊥l2,则实数a= .
15.已知直线l经过两条直线2x﹣3y+10=0和3x+4y﹣2=0的交点,且垂直于直线3x﹣2y+4=0,则直线l方程为 .
16.已知平面α,β,γ和直线a,b,则下列命题正确的是 (填序号).
①若α⊥β,β⊥γ,则α∥γ; ②若α∥β,β⊥γ,则α⊥γ;
③若α∩β=a,β∩γ=b,α⊥β,则a⊥b; ④若α⊥β,α∩β=a,a⊥b,则b⊥α;
⑤若a⊥α,a∥β,则α⊥β.
三.解答题(共8小题)
17.已知函数f(x)=x|x|﹣2x,x∈R.
(1)求y=f(x)的奇偶性;
(2)画出函数y=f(x)的图象;
(3)求y=f(x),x∈[﹣4,2]的值域.
18.已知二次函数f(x)=ax2+bx+c,满足f(1+x)=f(1﹣x)且不等式f(x)≤2x的解集为[1,3].
(1)求函数f(x)的解析式;
(2)方程f(x)=2x+k在(0,3]上有解,求实数k的取值范围.
19.设函数f(x)=loga(3+x)+loga(3﹣x),(a>0,且a≠1),f(1)=3.
(1)求a的值及f(x)的定义域;
(2)判断f(x)的奇偶性,并给出证明;
(3)求函数f(x)在[1,2]上的值域.
20.直线l过点(1,4),且倾斜角为45°.
(1)求直线l的方程;
(2)求直线l与坐标轴所围成的三角形面积.
21.已知四棱锥P﹣ABCD中,底面ABCD是直角梯形,∠BAD=90°,CD=2AB=2AD,侧面PAD是正三角形且垂直于面ABCD,E是PC中点.
3364230198120(1)求证:BE∥面PAD;
(2)求证:BE⊥平面PCD.
22.如图,在正方体ABCD﹣A1B1C1D1中,E、F分别为AB1、BD的中点.
(1)求证:EF∥平面BCC1B1;
(2)求直线EF与直线AA1所成的角.
3735705135890
2020年12月9日数学周测
参考答案与试题解析
一.选择题(共20小题)
1.C 2 C 3 D 4 D 5D 6B 7B 8C 9D 10C 11A 12D
二.填空题(共4小题)
13(2019,2020)
14.﹣3;﹣
15.2x+3y﹣2=0.
16.②⑤.
三.解答题(共6小题)
17.
【解答】解:(1)函数的定义域为R,
∵f(﹣x)=﹣x|﹣x|﹣2(﹣x)=﹣x|x|+2x=﹣(x|x|﹣2x)=﹣f(x),
∴f(x)为奇函数,
(2)f(x)=x|x|﹣2x=,
图象如图所示:
(3)由f(﹣4)=﹣4×|4|﹣2×(﹣4)=﹣16+8=﹣8,f(2)=2×|2|﹣2×2=0,f(﹣1)=﹣1×|﹣1|﹣2×(﹣1)=1,
结合图象可得y=f(x),x∈[﹣4,2]的值域为[﹣8,1].
18.
【解答】解:(1)由f(1+x)=f(1﹣x)知:f(x)关于x=1对称,
故﹣=1,即b=﹣2a,
又f(x)≤2x的解集是[1,3],
即ax2﹣(2a+2)x+c=0的两根是1,3,
即,解得:,
故f(x)=x2﹣2x+3;
(2)方程f(x)=2x+k在(0,3]上有解,
即方程k=x2﹣4x+3在(0,3]上有解,
即y=k的图象和g(x)=x2﹣4x+3的图象在(0,3]上有交点,
g(x)=(x﹣2)2﹣1,对称轴是x=2,
故g(x)在(0,2)递减,在(2,3]递增,
g(0)=3,g(2)=﹣1,故x∈(0,3]时,g(x)∈[﹣1,3),
故﹣1≤k<3.
19.
【解答】解:(1)因为f(x)=loga(3+x)+loga(3﹣x)=,
由题意f(1)=loga8=3,
故a=2,
由可得﹣3<x<3,
故函数的定义域(﹣3,3);
(2)因为f(﹣x)=loga(9﹣x2)=f(x),即函数f(x)为偶函数,
(3)∵1≤x≤2,
所以5≤9﹣x2≤8,
当a=2>1时,函数的值域[loga5,loga8],
20.
【解答】解:(1)∵直线l过点(1,4),且倾斜角为45°,故它的斜率为tan45°=1,
故它的方程为 y﹣4=1×(x﹣1),即x﹣y+3=0.
(2)∵直线x﹣y+3=0和坐标轴的交点为(﹣3,0)、(0,3),
故它与坐标轴所围成的三角形面积为×3×3=.
21.
【解答】证明:(1)取PD的中点F,连接AF、EF,
∵E是PC中点,∴EF∥CD,EF=CD,
∵AB∥CD,CD=2AB,
∴EF∥AB,EF=AB,
∴四边形ABEF是平行四边形,
∴BE∥AF,
又BE?平面PAD,AF?平面PAD,
∴BE∥面PAD.
(2)∵面PAD⊥面ABCD,面PAD∩面ABCD=AD,CD⊥AD,
∴CD⊥面PAD,
∵AF?平面PAD,∴CD⊥AF,
∵等边三角形PAD,F为PD的中点,∴AF⊥PD,
又CD∩PD=D,CD、PD?平面PCD,∴AF⊥平面PCD,
∵AF∥BE,∴BE⊥平面PCD.
22.如图,D
【解答】解:(1)证明:连结AC,B1C,
∵F是正方形ABCD对角线BC的中点,
∴F是AC的中点,
∵E是AB1的中点,∴EF∥B1C,
又EF?平面BCC1B1,B1C?面BCC1B1,
∴EF∥平面BCC1B1.
(2)由(1)知EF∥B1C,且AA1∥BB1,
∴直线EF与直线AA1所成角为直线B1C与直线BB1所成角,
∵正方形BCC1B1中,∠BB1C=45°,
∴直线EF与直线AA1所成的角为45°.
3049905102870
同课章节目录
