华东师大版七年级数学下册第10章 轴对称、平移与旋转单元测试题(word版 含答案)
文档属性
| 名称 | 华东师大版七年级数学下册第10章 轴对称、平移与旋转单元测试题(word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 728.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 00:00:00 | ||
图片预览


文档简介
第10章 轴对称、平移与旋转
一、选择题(本大题共10个小题,每题3分,共30分)
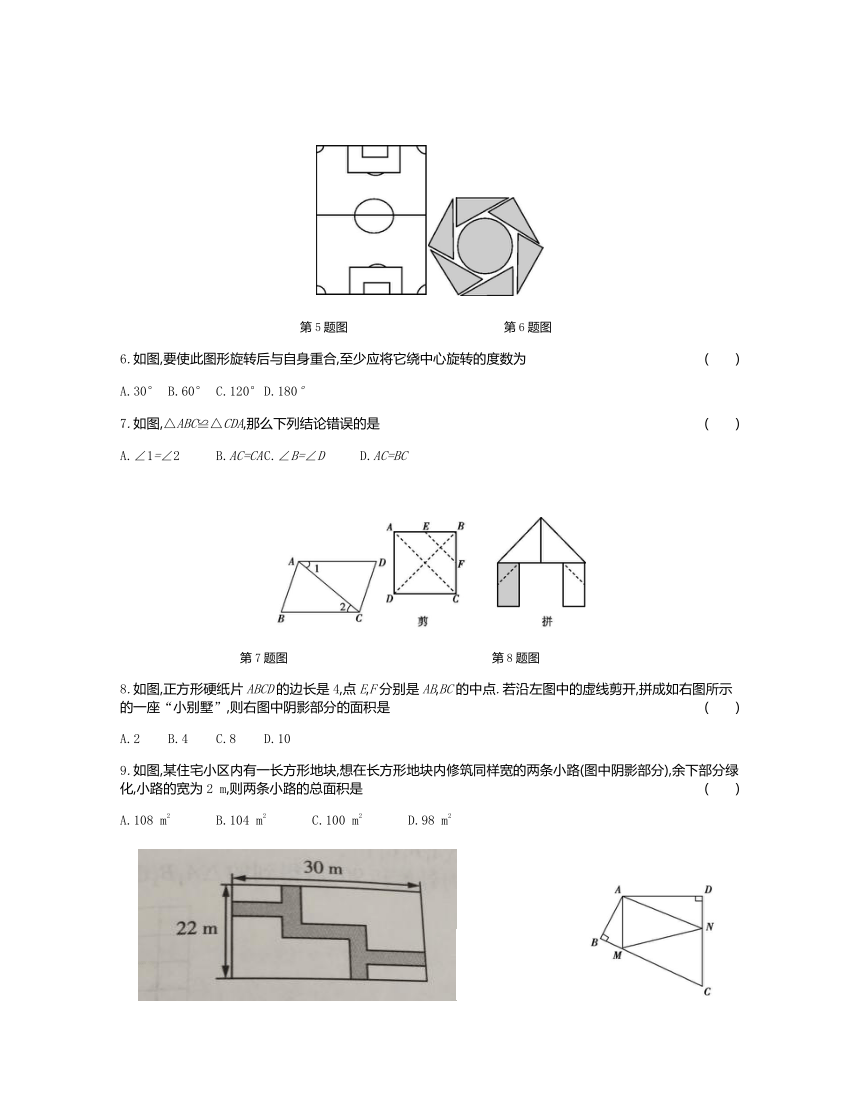
1.以下标志中,轴对称图形的个数是( )
A.0 B.1 C.2 D.3
2.将如图所示的图案以圆心为中心旋转180°后得到的图案是( )
A B C D
3.在下列各组图形中,是全等图形的是( )
A B C D
4. 把一张长方形纸片按如图①、图②的方式从右向左连续对折两次后得到图③,再在图③中挖去一个如图所示的三角形小孔,则重新展开后得到的图形是( )
A B C D
5.某学校足球场的平面示意图如图所示,它是轴对称图形,其对称轴的条数为( )
A.1 B.2 C.3 D.4
第5题图 第6题图
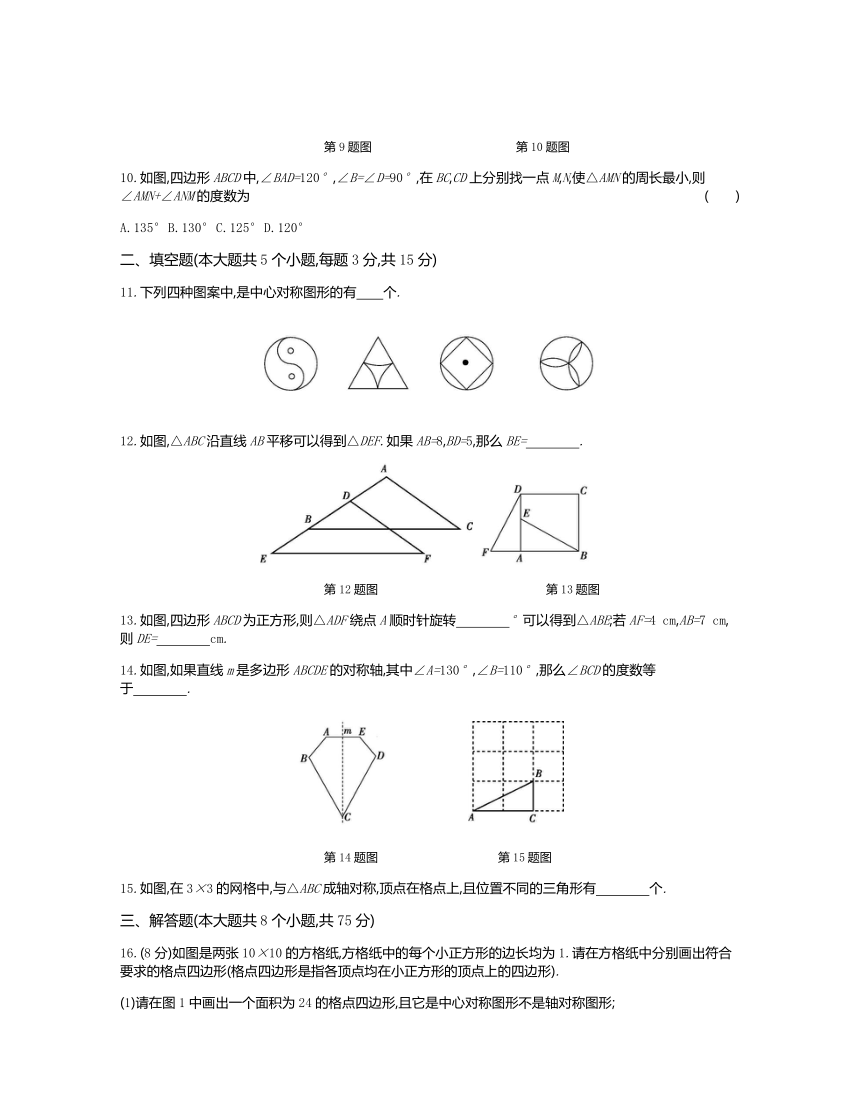
6.如图,要使此图形旋转后与自身重合,至少应将它绕中心旋转的度数为( )
A.30° B.60° C.120° D.180°
7.如图,△ABC≌△CDA,那么下列结论错误的是( )
A.∠1=∠2 B.AC=CA C.∠B=∠D D.AC=BC
第7题图 第8题图
8.如图,正方形硬纸片ABCD的边长是4,点E,F分别是AB,BC的中点.若沿左图中的虚线剪开,拼成如右图所示的一座“小别墅”,则右图中阴影部分的面积是( )
A.2 B.4 C.8 D.10
9.如图,某住宅小区内有一长方形地块,想在长方形地块内修筑同样宽的两条小路(图中阴影部分),余下部分绿化,小路的宽为2 m,则两条小路的总面积是( )
A.108 m2 B.104 m2 C.100 m2 D.98 m2
第9题图 第10题图
10.如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN的周长最小,则∠AMN+∠ANM的度数为( )
A.135° B.130° C.125° D.120°
二、填空题(本大题共5个小题,每题3分,共15分)
11.下列四种图案中,是中心对称图形的有 个.?
12.如图,△ABC沿直线AB平移可以得到△DEF.如果AB=8,BD=5,那么BE= .?
第12题图 第13题图
13.如图,四边形ABCD为正方形,则△ADF绕点A顺时针旋转 °可以得到△ABE;若AF=4 cm,AB=7 cm,则DE= cm.?
14.如图,如果直线m是多边形ABCDE的对称轴,其中∠A=130°,∠B=110°,那么∠BCD的度数等于 .?
第14题图 第15题图
15.如图,在3×3的网格中,与△ABC成轴对称,顶点在格点上,且位置不同的三角形有 个.?
三、解答题(本大题共8个小题,共75分)
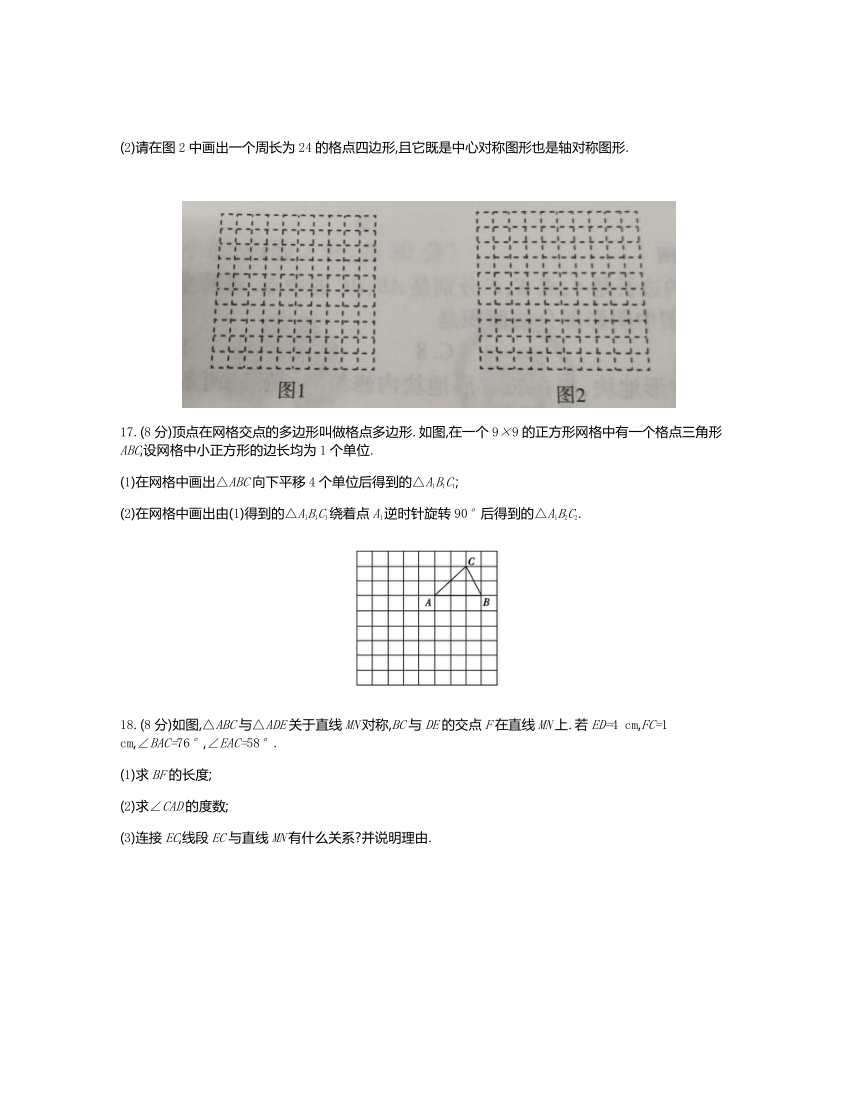
16.(8分)如图是两张10×10的方格纸,方格纸中的每个小正方形的边长均为1.请在方格纸中分别画出符合要求的格点四边形(格点四边形是指各顶点均在小正方形的顶点上的四边形).
(1)请在图1中画出一个面积为24的格点四边形,且它是中心对称图形不是轴对称图形;
(2)请在图2中画出一个周长为24的格点四边形,且它既是中心对称图形也是轴对称图形.
17.(8分)顶点在网格交点的多边形叫做格点多边形.如图,在一个9×9的正方形网格中有一个格点三角形ABC,设网格中小正方形的边长均为1个单位.
(1)在网格中画出△ABC向下平移4个单位后得到的△A1B1C1;
(2)在网格中画出由(1)得到的△A1B1C1绕着点A1逆时针旋转90°后得到的△A1B2C2.
18.(8分)如图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.若ED=4 cm,FC=1 cm,∠BAC=76°,∠EAC=58°.
(1)求BF的长度;
(2)求∠CAD的度数;
(3)连接EC,线段EC与直线MN有什么关系?并说明理由.
19.(9分)世界上因为有了圆的图案,万物才显得富有生机,如图所示的几个图形,是来自现实生活中的圆与其他图形结合在一起构成的轴对称图形,请你在后面的两个图中,分别画出与前面不重复的轴对称图形.
20.(10分)如图,在直角三角形ABC中,∠ACB=90°,∠A=37°,将△ABC沿AB方向平移得到△DEF.
(1)试求出∠E的度数;
(2)若AE=9 cm,DB=2 cm,求出CF的长度.
21.(10分)如图,△ABC≌△ADE,∠BAD=52°.
(1)求∠EAC的度数;
(2)△ABC怎样运动才能和△ADE重合?
22.(10分)如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F.若DE=7,BC=4,∠D=35°,∠C=60°.
(1)求线段AE的长;
(2)求∠DFA的度数.
23.(12分)取一副直角三角尺按图1拼接,其中∠ACD=30°,∠ACB=45°.
(1)如图2,三角尺ACD固定,将三角尺ABC绕点A按顺时针方向旋转一定的角度得到△ABC'.当∠CAC'=15°时,请你判断AB与CD的位置关系,并说明理由.
(2)如图3,三角尺ACD固定,将三角尺ABC绕点A按逆时针方向旋转一定的角度得到△ABC',猜想当∠CAC'为多少度时,能使CD∥BC',并说明理由.
584835205740
答案
题号
1
2
3
4
5
6
7
8
9
10
答案
D
D
A
C
B
B
D
B
C
D
11.2 12.3 13.90 3 14.60° 15.8
16. 答案不唯一.(1)如图1所示.
(2)如图2所示.
17. (1)(2)如图所示.
18. (1)∵△ABC与△ADE关于直线MN对称,∴BC=ED=4 cm,
∴BF=BC-FC=3 cm.
(2)∵△ABC与△ADE关于直线MN对称,
∴∠EAD=∠BAC=76°,
∴∠CAD=∠EAD-∠EAC=76°-58°=18°.
(3)直线MN垂直平分线段EC.理由如下:
∵E,C关于直线MN对称,
∴直线MN垂直平分线段EC.
19. 此题为开放性试题,只要是轴对称图形即可,以下图形供参考.(画出两种即可)
20. (1)∵在直角三角形ABC中,∠ACB=90°,∠A=37°,
∴∠CBA=90°-37°=53°,
由平移得,∠E=∠CBA=53°.
(2)由平移得,AD=BE=CF,
∵AE=9 cm,DB=2 cm,
∴AD=BE=12×(9-2)=3.5(cm),
∴CF=3.5 cm.
21. (1)由△ABC≌△ADE,得∠BAC=∠DAE,
所以∠BAC-∠BAE=∠DAE-∠BAE,
所以∠EAC=∠BAD=52°.
(2)△ABC绕点A顺时针旋转52°即可与△ADE重合.(答案不唯一)
22. (1)因为△ABC≌△DEB,所以AB=DE,BE=BC,
所以AE=AB-BE=DE-BC=7-4=3.
(2)因为△ABC≌△DEB,
所以∠A=∠D,∠C=∠ABD,
由三角形外角的性质,得∠AED=∠D+∠ABD=∠D+∠C=35°+60°=95°,
所以∠DFA=∠A+∠AED=35°+95°=130°.
23. (1)AB∥CD.理由如下:
∵∠BAC=∠BAC'-∠CAC'=45°-15°=30°,
∴∠BAC=∠C=30°,
∴AB∥CD.
(2)当∠CAC'=75°时,能使CD∥BC'.理由如下:
延长BA交CD于点E.
当∠CAC'=75°时,∵∠BAC'=45°,
∴∠BAC=75°+45°=120°.
又∵∠BAC=∠AEC+∠ACD,
∴∠AEC=120°-30°=90°,
又∵∠B=90°,
∴∠B+∠AEC=90°+90°=180°,
∴CD∥BC'.
一、选择题(本大题共10个小题,每题3分,共30分)
1.以下标志中,轴对称图形的个数是( )
A.0 B.1 C.2 D.3
2.将如图所示的图案以圆心为中心旋转180°后得到的图案是( )
A B C D
3.在下列各组图形中,是全等图形的是( )
A B C D
4. 把一张长方形纸片按如图①、图②的方式从右向左连续对折两次后得到图③,再在图③中挖去一个如图所示的三角形小孔,则重新展开后得到的图形是( )
A B C D
5.某学校足球场的平面示意图如图所示,它是轴对称图形,其对称轴的条数为( )
A.1 B.2 C.3 D.4
第5题图 第6题图
6.如图,要使此图形旋转后与自身重合,至少应将它绕中心旋转的度数为( )
A.30° B.60° C.120° D.180°
7.如图,△ABC≌△CDA,那么下列结论错误的是( )
A.∠1=∠2 B.AC=CA C.∠B=∠D D.AC=BC
第7题图 第8题图
8.如图,正方形硬纸片ABCD的边长是4,点E,F分别是AB,BC的中点.若沿左图中的虚线剪开,拼成如右图所示的一座“小别墅”,则右图中阴影部分的面积是( )
A.2 B.4 C.8 D.10
9.如图,某住宅小区内有一长方形地块,想在长方形地块内修筑同样宽的两条小路(图中阴影部分),余下部分绿化,小路的宽为2 m,则两条小路的总面积是( )
A.108 m2 B.104 m2 C.100 m2 D.98 m2
第9题图 第10题图
10.如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN的周长最小,则∠AMN+∠ANM的度数为( )
A.135° B.130° C.125° D.120°
二、填空题(本大题共5个小题,每题3分,共15分)
11.下列四种图案中,是中心对称图形的有 个.?
12.如图,△ABC沿直线AB平移可以得到△DEF.如果AB=8,BD=5,那么BE= .?
第12题图 第13题图
13.如图,四边形ABCD为正方形,则△ADF绕点A顺时针旋转 °可以得到△ABE;若AF=4 cm,AB=7 cm,则DE= cm.?
14.如图,如果直线m是多边形ABCDE的对称轴,其中∠A=130°,∠B=110°,那么∠BCD的度数等于 .?
第14题图 第15题图
15.如图,在3×3的网格中,与△ABC成轴对称,顶点在格点上,且位置不同的三角形有 个.?
三、解答题(本大题共8个小题,共75分)
16.(8分)如图是两张10×10的方格纸,方格纸中的每个小正方形的边长均为1.请在方格纸中分别画出符合要求的格点四边形(格点四边形是指各顶点均在小正方形的顶点上的四边形).
(1)请在图1中画出一个面积为24的格点四边形,且它是中心对称图形不是轴对称图形;
(2)请在图2中画出一个周长为24的格点四边形,且它既是中心对称图形也是轴对称图形.
17.(8分)顶点在网格交点的多边形叫做格点多边形.如图,在一个9×9的正方形网格中有一个格点三角形ABC,设网格中小正方形的边长均为1个单位.
(1)在网格中画出△ABC向下平移4个单位后得到的△A1B1C1;
(2)在网格中画出由(1)得到的△A1B1C1绕着点A1逆时针旋转90°后得到的△A1B2C2.
18.(8分)如图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.若ED=4 cm,FC=1 cm,∠BAC=76°,∠EAC=58°.
(1)求BF的长度;
(2)求∠CAD的度数;
(3)连接EC,线段EC与直线MN有什么关系?并说明理由.
19.(9分)世界上因为有了圆的图案,万物才显得富有生机,如图所示的几个图形,是来自现实生活中的圆与其他图形结合在一起构成的轴对称图形,请你在后面的两个图中,分别画出与前面不重复的轴对称图形.
20.(10分)如图,在直角三角形ABC中,∠ACB=90°,∠A=37°,将△ABC沿AB方向平移得到△DEF.
(1)试求出∠E的度数;
(2)若AE=9 cm,DB=2 cm,求出CF的长度.
21.(10分)如图,△ABC≌△ADE,∠BAD=52°.
(1)求∠EAC的度数;
(2)△ABC怎样运动才能和△ADE重合?
22.(10分)如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F.若DE=7,BC=4,∠D=35°,∠C=60°.
(1)求线段AE的长;
(2)求∠DFA的度数.
23.(12分)取一副直角三角尺按图1拼接,其中∠ACD=30°,∠ACB=45°.
(1)如图2,三角尺ACD固定,将三角尺ABC绕点A按顺时针方向旋转一定的角度得到△ABC'.当∠CAC'=15°时,请你判断AB与CD的位置关系,并说明理由.
(2)如图3,三角尺ACD固定,将三角尺ABC绕点A按逆时针方向旋转一定的角度得到△ABC',猜想当∠CAC'为多少度时,能使CD∥BC',并说明理由.
584835205740
答案
题号
1
2
3
4
5
6
7
8
9
10
答案
D
D
A
C
B
B
D
B
C
D
11.2 12.3 13.90 3 14.60° 15.8
16. 答案不唯一.(1)如图1所示.
(2)如图2所示.
17. (1)(2)如图所示.
18. (1)∵△ABC与△ADE关于直线MN对称,∴BC=ED=4 cm,
∴BF=BC-FC=3 cm.
(2)∵△ABC与△ADE关于直线MN对称,
∴∠EAD=∠BAC=76°,
∴∠CAD=∠EAD-∠EAC=76°-58°=18°.
(3)直线MN垂直平分线段EC.理由如下:
∵E,C关于直线MN对称,
∴直线MN垂直平分线段EC.
19. 此题为开放性试题,只要是轴对称图形即可,以下图形供参考.(画出两种即可)
20. (1)∵在直角三角形ABC中,∠ACB=90°,∠A=37°,
∴∠CBA=90°-37°=53°,
由平移得,∠E=∠CBA=53°.
(2)由平移得,AD=BE=CF,
∵AE=9 cm,DB=2 cm,
∴AD=BE=12×(9-2)=3.5(cm),
∴CF=3.5 cm.
21. (1)由△ABC≌△ADE,得∠BAC=∠DAE,
所以∠BAC-∠BAE=∠DAE-∠BAE,
所以∠EAC=∠BAD=52°.
(2)△ABC绕点A顺时针旋转52°即可与△ADE重合.(答案不唯一)
22. (1)因为△ABC≌△DEB,所以AB=DE,BE=BC,
所以AE=AB-BE=DE-BC=7-4=3.
(2)因为△ABC≌△DEB,
所以∠A=∠D,∠C=∠ABD,
由三角形外角的性质,得∠AED=∠D+∠ABD=∠D+∠C=35°+60°=95°,
所以∠DFA=∠A+∠AED=35°+95°=130°.
23. (1)AB∥CD.理由如下:
∵∠BAC=∠BAC'-∠CAC'=45°-15°=30°,
∴∠BAC=∠C=30°,
∴AB∥CD.
(2)当∠CAC'=75°时,能使CD∥BC'.理由如下:
延长BA交CD于点E.
当∠CAC'=75°时,∵∠BAC'=45°,
∴∠BAC=75°+45°=120°.
又∵∠BAC=∠AEC+∠ACD,
∴∠AEC=120°-30°=90°,
又∵∠B=90°,
∴∠B+∠AEC=90°+90°=180°,
∴CD∥BC'.
