华东师大版七年级数学下册 第9章 多边形单元测试题(word版 含答案)
文档属性
| 名称 | 华东师大版七年级数学下册 第9章 多边形单元测试题(word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 674.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 00:00:00 | ||
图片预览



文档简介
第9章多边形
一.选择题(本大题共10个小题,每题3分,共30分)
1.下列物品不是利用三角形稳定性的是( )
A.长方形门框的斜拉条 B.三角形房架
C.埃及金字塔 D.学校的电动伸缩大门
2.在下列长度的三条线段中,不能组成三角形的是( )
A.2 cm,3 cm,4 cm B.3 cm,6 cm,6 cm
C.2 cm,2 cm,6 cm D.5 cm,6 cm,7 cm
3.在△ABC中,若一个内角等于另外两个内角的差,则( )
A.必有一个内角等于90° B.必有一个内角等于45°
C.必有一个内角等于60° D.必有一个内角等于30°
4.如图,∠1,∠2,∠3,∠4一定满足的关系式是( )
A.∠1+∠2=∠3+∠4
B.∠1+∠2=∠4-∠3
C.∠1+∠4=∠2+∠3
D.∠1+∠4=∠2-∠3
5.若一个多边形的内角和比外角和大360°,则这个多边形的边数为( )
A.4 B.5 C.6 D.7
6.三角形三个外角之比为2∶4∶3,则它的最小内角是( )
A.20° B.30° C.40° D.以上都不对
7.在给定的下列条件中,不能判定三角形是直角三角形的是( )
A.∠A∶∠B∶∠C=1∶2∶3 B.∠A+∠B=∠C
C.∠A=12∠B=13∠C D.∠A=2∠B=3∠C
8.如图,将△ABC的三个角分别沿DE,HG,EF翻折,三个顶点均落在点O处,则∠1+∠2的度数为( )
A.120° B.135° C.150° D.180°
第8题图 第9题图
9.在如图所示的七边形ABCDEFG中,∠1,∠2,∠3,∠4四个角的外角和为180°,∠5的外角为60°,BP,DP分别平分∠ABC,∠CDE,则∠BPD的度数是( )
A.130° B.120° C.110° D.100°
10.如图,若干个相同的正五边形排成环状.图中所示的是前3个正五边形,要完成这一圆环还需正五边形的个数为( )
A.6 B.7 C.8 D.9
二、填空题(本大题共5个小题,每题3分,共15分)
11.如果一个三角形的三条高的交点恰是该三角形的一个顶点,那么这个三角形的形状是 .?
12.过m边形的一个顶点有7条对角线,n边形没有对角线,则m+n的值是 .?
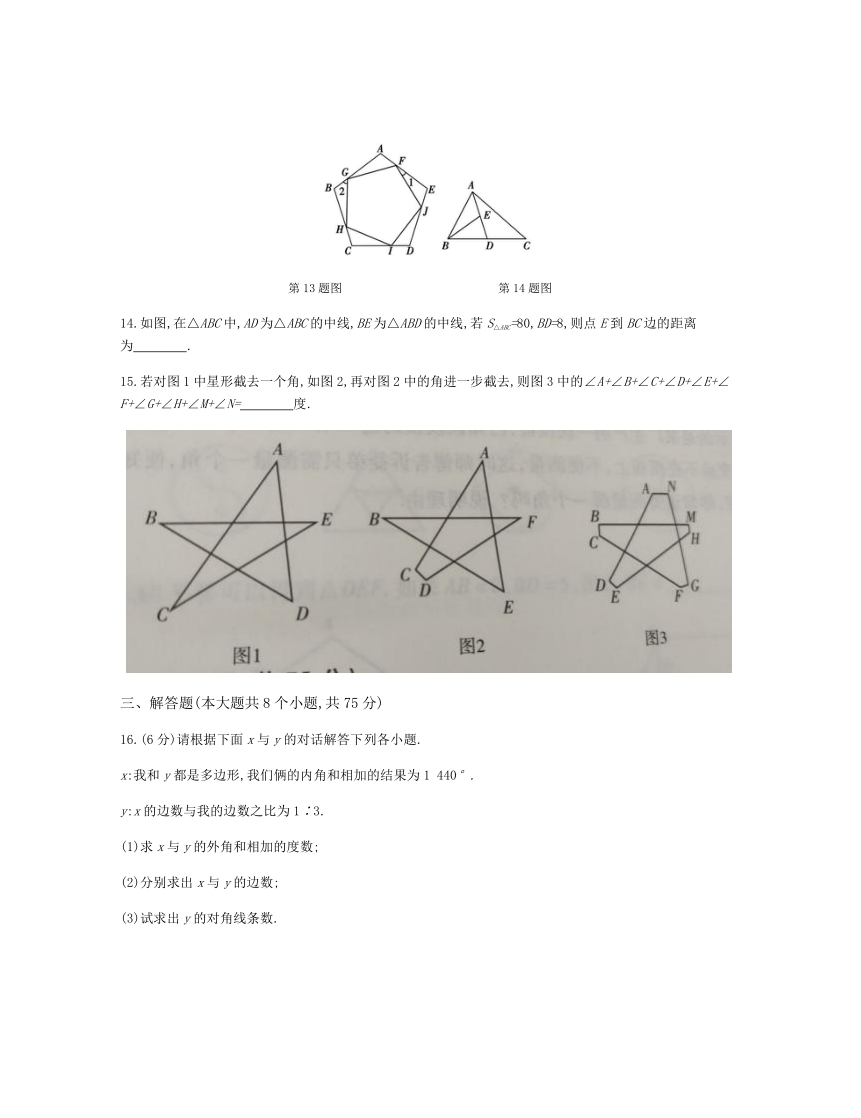
13.如图,正五边形FGHIJ的顶点在正五边形ABCDE的边上.若∠1=20°,则∠2= °.?
第13题图 第14题图
14.如图,在△ABC中,AD为△ABC的中线,BE为△ABD的中线,若S△ABC=80,BD=8,则点E到BC边的距离为 .?
15.若对图1中星形截去一个角,如图2,再对图2中的角进一步截去,则图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N= 度.?
三、解答题(本大题共8个小题,共75分)
16.(6分)请根据下面x与y的对话解答下列各小题.
x:我和y都是多边形,我们俩的内角和相加的结果为1 440°.
y:x的边数与我的边数之比为1∶3.
(1)求x与y的外角和相加的度数;
(2)分别求出x与y的边数;
(3)试求出y的对角线条数.
17.(8分)将一副三角尺拼成如图1所示的形状,画出示意图如图2所示,过点C作CF平分∠DCE交DE于点F.
(1)试说明:CF∥AB.
(2)求∠DFC的度数.
18.(9分)已知a,b,c为△ABC的三边长,b,c满足(b-2)2+|c-3|=0,且a为方程|a-4|=2的解,求△ABC的周长,并判断△ABC的形状.
19.(9分)如图所示的是某厂生产的一块模板,已知该模板的边AB∥CF,CD∥AE.按规定AB,CD的延长线相交成80°角,因交点不在模板上,不便测量,这时师傅告诉徒弟只需测量一个角,便知道AB,CD延长线的夹角是否符合规定,你知道需测量哪一个角吗?说明理由.
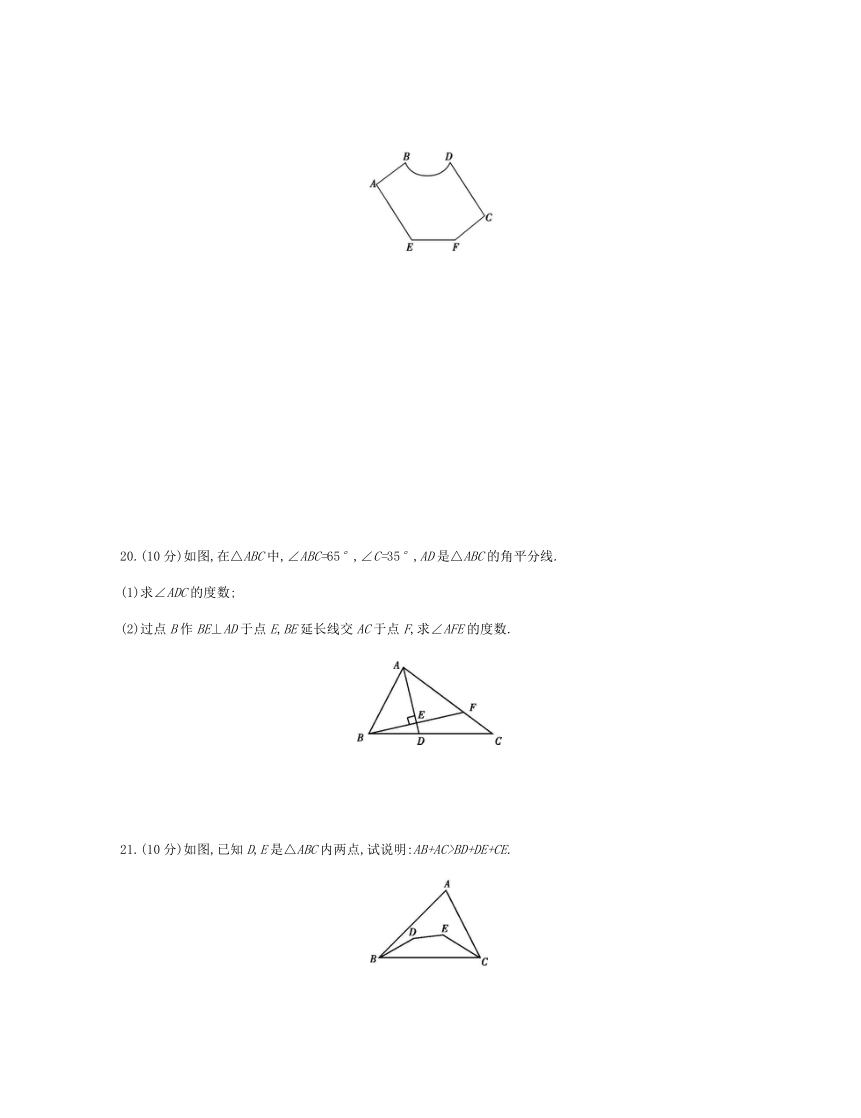
20.(10分)如图,在△ABC中,∠ABC=65°,∠C=35°,AD是△ABC的角平分线.
(1)求∠ADC的度数;
(2)过点B作BE⊥AD于点E,BE延长线交AC于点F,求∠AFE的度数.
21.(10分)如图,已知D,E是△ABC内两点,试说明:AB+AC>BD+DE+CE.
22.(11分)请回答下列问题:
(1)如图1,有一块直角三角尺XYZ放置在△ABC上,恰好三角尺XYZ的两条直角边XY,XZ分别经过点B,C,已知在△ABC中,∠A=30°,则∠ABC+∠ACB= °,∠ABX+∠ACX= °;?
(2)如图2,改变(1)中直角三角尺XYZ的位置,使三角尺XYZ的两条直角边XY,XZ仍然分别经过B,C两点,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.
23.(12分)在直角三角形ABC中,∠C=90°,点D,E分别是边AC,BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图1,且∠α=50°,则∠1+∠2= ;?
(2)若点P在斜边AB上运动,如图2,则∠α,∠1,∠2之间的关系为 ;?
(3)如图3,若点P在斜边BA的延长线上运动(CE(4)若点P运动到△ABC外(只需研究图4的情形),则∠α,∠1,∠2之间有何关系?并说明理由.
答案
题号
1
2
3
4
5
6
7
8
9
10
答案
D
C
A
D
C
A
C
D
B
B
11.直角三角形 12.13 13.52 14.5 15.1 080
16. (1)360°+360°=720°.
(2)设x的边数为n,y的边数为3n,
由题意得180(n-2)+180(3n-2)=1 440,
解得n=3,
∴3n=9,
∴x与y的边数分别为3和9.
(3)92×(9-3)=27(条).
答:y共有27条对角线.
17. (1)由题意,知∠D=30°,∠3=45°,∠DCE=90°.
因为CF平分∠DCE,所以∠1=∠2=12∠DCE=45°,
所以∠1=∠3,所以CF∥AB.
(2)∠DFC=180°-∠1-∠D=180°-45°-30°=105°.
18. ∵(b-2)2+|c-3|=0,
∴b-2=0,c-3=0,
解得b=2,c=3.
∵a为方程|a-4|=2的解,
∴a-4=±2,
解得a=6或2.
∵a,b,c为△ABC的三边长,b+c<6,
∴a=6不合题意舍去,
∴只能取a=2,
∴△ABC的周长为2+2+3=7,△ABC是等腰三角形.
19. 只需要测量∠DCF或∠BAE是否等于100°,就能够知道AB,CD延长线的夹角是否符合规定.理由如下:
连接AF.
因为AB∥CF,
所以∠BAF+∠AFC=180°.
因为∠EAF+∠E +∠AFE=180°,
所以∠BAE+∠E +∠EFC=360°.
若∠DCF=100°,则AB,CD延长线的夹角为540°-360°-100°=80°,即符合规定.
同理,若连接CE,则可得∠AEF+∠F +∠DCF=360°,若∠BAE=100°,则也符合规定.
20. (1)∵∠ABC=65°,∠C=35°,
∴∠BAC=180°-∠ABC-∠C=80°,
又∵AD是△ABC的角平分线,
∴∠DAF=12∠BAC=40°,
∴∠ADC=180°-∠C-∠DAC=180°-40°-35°=105°.
(2)∵BE⊥AD,∴∠AEF=90°,
由(1)可得∠EAF=40°,
∴∠AFE=180°-∠AEF-∠EAF=180°-40°-90°=50°.
21. 如图,延长ED,DE分别交AB,AC于点F,G.
在△AFG中,AF+AG>FG,
在△BFD中,FB+FD>BD,
在△EGC中,EG+GC>CE,
所以AF+AG+FB+FD+EG+GC>FG+BD+CE,
所以AB+FD+EG+AC>FG+BD+CE,即AB+AC>FG-FD-EG+BD+CE.
因为FD+ED+EG=FG,所以AB+AC>BD+DE+CE.
22. (1)150 60
(2)不变化.
∵∠A=30°,∴∠ABC+∠ACB=150°,
∵∠X=90°,∴∠XBC+∠XCB=90°,
∴∠ABX+∠ACX=(∠ABC -∠XBC)+(∠ACB -∠XCB)=(∠ABC+∠ACB)-(∠XBC+∠XCB)=150°-90°=60°.
23. (1)140°
连接PC,可得∠1=∠PCD+∠CPD,∠2=∠PCE+∠CPE,
∴∠1+∠2=∠PCD+∠CPD+∠PCE+∠CPE=∠DPE+∠ECD,
而∠DPE=∠α=50°,∠ECD=90°,
∴∠1+∠2=50°+90°=140°.
(2)∠1+∠2=90°+∠α
如图1,连接PC.
图1
∵∠1=∠PCD+∠CPD,∠2=∠PCE+∠CPE,
∴∠1+∠2=∠PCD+∠CPD+∠PCE+∠CPE=∠DPE+∠ECD.
∵∠ECD=90°,∠DPE=∠α,
∴∠1+∠2=90°+∠α.
(3)∠2-∠1=90°+∠α或∠2=∠1+90°或∠1-∠2=∠α-90°
如图2,∠2=∠C+∠1+∠α,
∴∠2-∠1=90°+∠α;
如图3,∠α=0°,∠2=∠1+90°;
如图4,∵∠2=∠1-∠α+∠C,
∴∠1-∠2=∠α-90°.
图4
故∠α,∠1,∠2之间的关系为∠2-∠1=90°+∠α或∠2=∠1+90°或∠1-∠2=∠α-90°.
(4)关系是∠2=90°+∠1-∠α,理由如下:
如图5,∵∠PFD=∠EFC,
∴180°-∠PFD=180°-∠EFC,
∴∠α+180°-∠1=∠C+180°-∠2,
∴∠2=90°+∠1-∠α.
图5
一.选择题(本大题共10个小题,每题3分,共30分)
1.下列物品不是利用三角形稳定性的是( )
A.长方形门框的斜拉条 B.三角形房架
C.埃及金字塔 D.学校的电动伸缩大门
2.在下列长度的三条线段中,不能组成三角形的是( )
A.2 cm,3 cm,4 cm B.3 cm,6 cm,6 cm
C.2 cm,2 cm,6 cm D.5 cm,6 cm,7 cm
3.在△ABC中,若一个内角等于另外两个内角的差,则( )
A.必有一个内角等于90° B.必有一个内角等于45°
C.必有一个内角等于60° D.必有一个内角等于30°
4.如图,∠1,∠2,∠3,∠4一定满足的关系式是( )
A.∠1+∠2=∠3+∠4
B.∠1+∠2=∠4-∠3
C.∠1+∠4=∠2+∠3
D.∠1+∠4=∠2-∠3
5.若一个多边形的内角和比外角和大360°,则这个多边形的边数为( )
A.4 B.5 C.6 D.7
6.三角形三个外角之比为2∶4∶3,则它的最小内角是( )
A.20° B.30° C.40° D.以上都不对
7.在给定的下列条件中,不能判定三角形是直角三角形的是( )
A.∠A∶∠B∶∠C=1∶2∶3 B.∠A+∠B=∠C
C.∠A=12∠B=13∠C D.∠A=2∠B=3∠C
8.如图,将△ABC的三个角分别沿DE,HG,EF翻折,三个顶点均落在点O处,则∠1+∠2的度数为( )
A.120° B.135° C.150° D.180°
第8题图 第9题图
9.在如图所示的七边形ABCDEFG中,∠1,∠2,∠3,∠4四个角的外角和为180°,∠5的外角为60°,BP,DP分别平分∠ABC,∠CDE,则∠BPD的度数是( )
A.130° B.120° C.110° D.100°
10.如图,若干个相同的正五边形排成环状.图中所示的是前3个正五边形,要完成这一圆环还需正五边形的个数为( )
A.6 B.7 C.8 D.9
二、填空题(本大题共5个小题,每题3分,共15分)
11.如果一个三角形的三条高的交点恰是该三角形的一个顶点,那么这个三角形的形状是 .?
12.过m边形的一个顶点有7条对角线,n边形没有对角线,则m+n的值是 .?
13.如图,正五边形FGHIJ的顶点在正五边形ABCDE的边上.若∠1=20°,则∠2= °.?
第13题图 第14题图
14.如图,在△ABC中,AD为△ABC的中线,BE为△ABD的中线,若S△ABC=80,BD=8,则点E到BC边的距离为 .?
15.若对图1中星形截去一个角,如图2,再对图2中的角进一步截去,则图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N= 度.?
三、解答题(本大题共8个小题,共75分)
16.(6分)请根据下面x与y的对话解答下列各小题.
x:我和y都是多边形,我们俩的内角和相加的结果为1 440°.
y:x的边数与我的边数之比为1∶3.
(1)求x与y的外角和相加的度数;
(2)分别求出x与y的边数;
(3)试求出y的对角线条数.
17.(8分)将一副三角尺拼成如图1所示的形状,画出示意图如图2所示,过点C作CF平分∠DCE交DE于点F.
(1)试说明:CF∥AB.
(2)求∠DFC的度数.
18.(9分)已知a,b,c为△ABC的三边长,b,c满足(b-2)2+|c-3|=0,且a为方程|a-4|=2的解,求△ABC的周长,并判断△ABC的形状.
19.(9分)如图所示的是某厂生产的一块模板,已知该模板的边AB∥CF,CD∥AE.按规定AB,CD的延长线相交成80°角,因交点不在模板上,不便测量,这时师傅告诉徒弟只需测量一个角,便知道AB,CD延长线的夹角是否符合规定,你知道需测量哪一个角吗?说明理由.
20.(10分)如图,在△ABC中,∠ABC=65°,∠C=35°,AD是△ABC的角平分线.
(1)求∠ADC的度数;
(2)过点B作BE⊥AD于点E,BE延长线交AC于点F,求∠AFE的度数.
21.(10分)如图,已知D,E是△ABC内两点,试说明:AB+AC>BD+DE+CE.
22.(11分)请回答下列问题:
(1)如图1,有一块直角三角尺XYZ放置在△ABC上,恰好三角尺XYZ的两条直角边XY,XZ分别经过点B,C,已知在△ABC中,∠A=30°,则∠ABC+∠ACB= °,∠ABX+∠ACX= °;?
(2)如图2,改变(1)中直角三角尺XYZ的位置,使三角尺XYZ的两条直角边XY,XZ仍然分别经过B,C两点,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.
23.(12分)在直角三角形ABC中,∠C=90°,点D,E分别是边AC,BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图1,且∠α=50°,则∠1+∠2= ;?
(2)若点P在斜边AB上运动,如图2,则∠α,∠1,∠2之间的关系为 ;?
(3)如图3,若点P在斜边BA的延长线上运动(CE
答案
题号
1
2
3
4
5
6
7
8
9
10
答案
D
C
A
D
C
A
C
D
B
B
11.直角三角形 12.13 13.52 14.5 15.1 080
16. (1)360°+360°=720°.
(2)设x的边数为n,y的边数为3n,
由题意得180(n-2)+180(3n-2)=1 440,
解得n=3,
∴3n=9,
∴x与y的边数分别为3和9.
(3)92×(9-3)=27(条).
答:y共有27条对角线.
17. (1)由题意,知∠D=30°,∠3=45°,∠DCE=90°.
因为CF平分∠DCE,所以∠1=∠2=12∠DCE=45°,
所以∠1=∠3,所以CF∥AB.
(2)∠DFC=180°-∠1-∠D=180°-45°-30°=105°.
18. ∵(b-2)2+|c-3|=0,
∴b-2=0,c-3=0,
解得b=2,c=3.
∵a为方程|a-4|=2的解,
∴a-4=±2,
解得a=6或2.
∵a,b,c为△ABC的三边长,b+c<6,
∴a=6不合题意舍去,
∴只能取a=2,
∴△ABC的周长为2+2+3=7,△ABC是等腰三角形.
19. 只需要测量∠DCF或∠BAE是否等于100°,就能够知道AB,CD延长线的夹角是否符合规定.理由如下:
连接AF.
因为AB∥CF,
所以∠BAF+∠AFC=180°.
因为∠EAF+∠E +∠AFE=180°,
所以∠BAE+∠E +∠EFC=360°.
若∠DCF=100°,则AB,CD延长线的夹角为540°-360°-100°=80°,即符合规定.
同理,若连接CE,则可得∠AEF+∠F +∠DCF=360°,若∠BAE=100°,则也符合规定.
20. (1)∵∠ABC=65°,∠C=35°,
∴∠BAC=180°-∠ABC-∠C=80°,
又∵AD是△ABC的角平分线,
∴∠DAF=12∠BAC=40°,
∴∠ADC=180°-∠C-∠DAC=180°-40°-35°=105°.
(2)∵BE⊥AD,∴∠AEF=90°,
由(1)可得∠EAF=40°,
∴∠AFE=180°-∠AEF-∠EAF=180°-40°-90°=50°.
21. 如图,延长ED,DE分别交AB,AC于点F,G.
在△AFG中,AF+AG>FG,
在△BFD中,FB+FD>BD,
在△EGC中,EG+GC>CE,
所以AF+AG+FB+FD+EG+GC>FG+BD+CE,
所以AB+FD+EG+AC>FG+BD+CE,即AB+AC>FG-FD-EG+BD+CE.
因为FD+ED+EG=FG,所以AB+AC>BD+DE+CE.
22. (1)150 60
(2)不变化.
∵∠A=30°,∴∠ABC+∠ACB=150°,
∵∠X=90°,∴∠XBC+∠XCB=90°,
∴∠ABX+∠ACX=(∠ABC -∠XBC)+(∠ACB -∠XCB)=(∠ABC+∠ACB)-(∠XBC+∠XCB)=150°-90°=60°.
23. (1)140°
连接PC,可得∠1=∠PCD+∠CPD,∠2=∠PCE+∠CPE,
∴∠1+∠2=∠PCD+∠CPD+∠PCE+∠CPE=∠DPE+∠ECD,
而∠DPE=∠α=50°,∠ECD=90°,
∴∠1+∠2=50°+90°=140°.
(2)∠1+∠2=90°+∠α
如图1,连接PC.
图1
∵∠1=∠PCD+∠CPD,∠2=∠PCE+∠CPE,
∴∠1+∠2=∠PCD+∠CPD+∠PCE+∠CPE=∠DPE+∠ECD.
∵∠ECD=90°,∠DPE=∠α,
∴∠1+∠2=90°+∠α.
(3)∠2-∠1=90°+∠α或∠2=∠1+90°或∠1-∠2=∠α-90°
如图2,∠2=∠C+∠1+∠α,
∴∠2-∠1=90°+∠α;
如图3,∠α=0°,∠2=∠1+90°;
如图4,∵∠2=∠1-∠α+∠C,
∴∠1-∠2=∠α-90°.
图4
故∠α,∠1,∠2之间的关系为∠2-∠1=90°+∠α或∠2=∠1+90°或∠1-∠2=∠α-90°.
(4)关系是∠2=90°+∠1-∠α,理由如下:
如图5,∵∠PFD=∠EFC,
∴180°-∠PFD=180°-∠EFC,
∴∠α+180°-∠1=∠C+180°-∠2,
∴∠2=90°+∠1-∠α.
图5
