人教版九年级上册数学学案:23.2中心对称(表格式 无答案)
文档属性
| 名称 | 人教版九年级上册数学学案:23.2中心对称(表格式 无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 57.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 23:21:33 | ||
图片预览

文档简介
“大集体”备课导学案基本模板
学段
人教版上册
年级
学科
数学
单元
第二十三章
旋转
课题
23.2.1
中心对称
课型
新课
主备学校
主备人
初审人
终审人
合作团队
数学备课组
教学目标
1、通过具体实例认识中心对称,了解中心对称的概念
2、掌握中心对称的性质,理解对应点所连线段被对称中心平分的性质.
教学重点
中心对称的概念和性质.
教学难点
理解中心对称的性质.
导学环节
课堂流程
学法指导
当堂反思
学习目标
通过具体实例认识中心对称,了解中心对称的概念,掌握中心对称的性质,理解对应点所连线段被对称中心平分的性质.
自读,明确当堂目标
自主学习
温故知新
1、什么是轴对称?成轴对称的两个图形有什么性质?2、旋转有哪些性质?
自主完成,
组内交流
设问导学
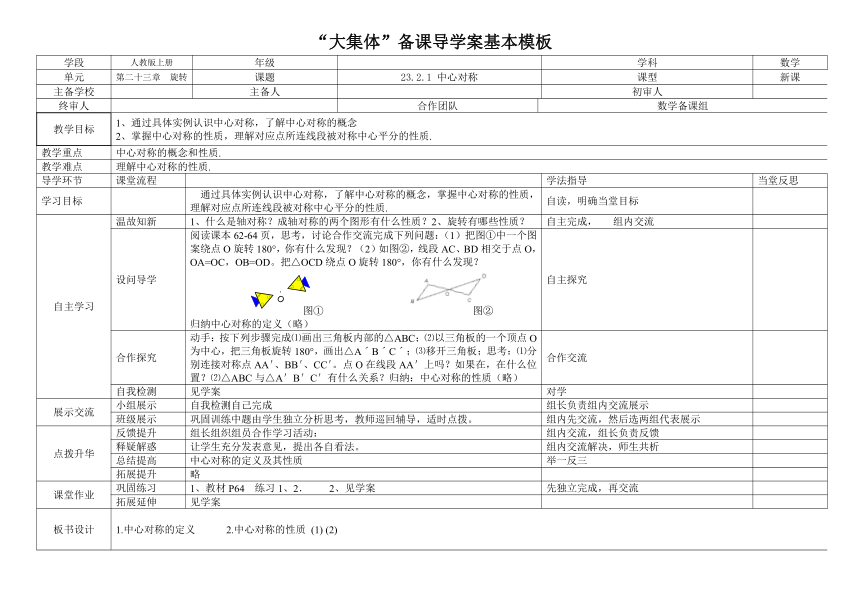
阅读课本62-64页,思考,讨论合作交流完成下列问题:(1)把图①中一个图案绕点O旋转180°,你有什么发现?(2)如图②,线段AC、BD相交于点O,OA=OC,OB=OD。把△OCD绕点O旋转180°,你有什么发现?
图①
图②
归纳中心对称的定义(略)
自主探究
合作探究
动手:按下列步骤完成⑴画出三角板内部的△ABC;⑵以三角板的一个顶点O为中心,把三角板旋转180°,画出△AˊBˊCˊ;⑶移开三角板;思考:⑴分别连接对称点AA'、BB'、CC'。点O在线段AA'上吗?如果在,在什么位置?⑵△ABC与△A'B'C'有什么关系?归纳:中心对称的性质(略)
合作交流
自我检测
见学案
对学
展示交流
小组展示
自我检测自己完成
组长负责组内交流展示
班级展示
巩固训练中题由学生独立分析思考,教师巡回辅导,适时点拨。
组内先交流,然后选两组代表展示
点拨升华
反馈提升
组长组织组员合作学习活动:
组内交流,组长负责反馈
释疑解惑
让学生充分发表意见,提出各自看法。
组内交流解决,师生共析
总结提高
中心对称的定义及其性质
举一反三
拓展提升
略
课堂作业
巩固练习
1、教材P64
练习1、2.
2、见学案
先独立完成,再交流
拓展延伸
见学案
板书设计
1.中心对称的定义
2.中心对称的性质
(1)
(2)
“大集体”备课导学案基本模板
学段
人教版上册
年级
学科
数学
单元
第二十三章
旋转
课题
23.2.2
中心对称图形
课型
新课
主备学校
主备人
初审人
终审人
合作团队
数学备课组
教学目标
1、正确认识什么是中心对称图形,理解中心对称图形的性质特点.
2、能理解中心对称和中心对称图形的异同.
教学重点
中心对称图形的有关概念及性质。
教学难点
中心对称与中心对称图形的联系与区别.
导学环节
课堂流程
学法指导
当堂反思
学习目标
正确认识什么是中心对称图形,理解中心对称图形的性质特点.掌握中心对称和中心对称图形的异同.
自读,明确当堂目标
自主学习
温故知新
什么叫中心对称、对称中心、关于中心的对称点?关于中心对称的两图形具有什么性质?
自主完成,
组内交流
设问导学
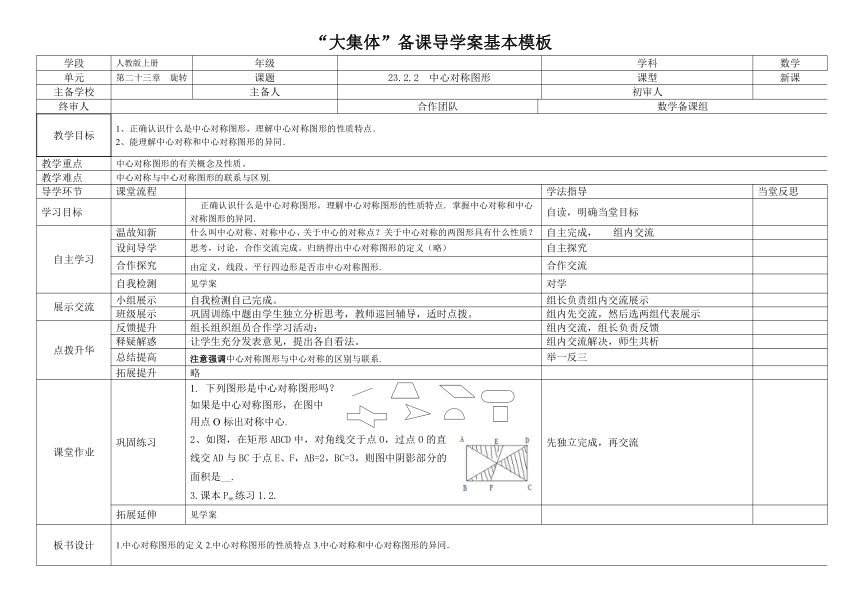
思考,讨论,合作交流完成。归纳得出中心对称图形的定义(略)
自主探究
合作探究
由定义,线段、平行四边形是否市中心对称图形.
合作交流
自我检测
见学案
对学
展示交流
小组展示
自我检测自己完成。
组长负责组内交流展示
班级展示
巩固训练中题由学生独立分析思考,教师巡回辅导,适时点拨。
组内先交流,然后选两组代表展示
点拨升华
反馈提升
组长组织组员合作学习活动:
组内交流,组长负责反馈
释疑解惑
让学生充分发表意见,提出各自看法。
组内交流解决,师生共析
总结提高
注意强调中心对称图形与中心对称的区别与联系.
举一反三
拓展提升
略
课堂作业
巩固练习
下列图形是中心对称图形吗?
如果是中心对称图形,在图中
用点O标出对称中心.
2、如图,在矩形ABCD中,对角线交于点O,过点O的直线交AD与BC于点E、F,AB=2,BC=3,则图中阴影部分的面积是__.
3.课本P66练习1.2.
先独立完成,再交流
拓展延伸
见学案
板书设计
1.中心对称图形的定义2.中心对称图形的性质特点3.中心对称和中心对称图形的异同.
“大集体”备课导学案基本模板
学段
人教版上册
年级
学科
数学
单元
第二十三章
旋转
课题
23.2.3关于原点对称的点的坐标
课型
新课
主备学校
主备人
初审人
终审人
合作团队
数学备课组
教学目标
1、正确认识关于原点对称的两点的坐标间的关系.
2、能运用关于原点成中心对称的点的坐标间的关系进行中心对称图形的变换.
教学重点
关于原点对称点的坐标.
教学难点
探究关于原点对称点的坐标.
导学环节
课堂流程
学法指导
当堂反思
学习目标
认识关于原点对称的两点的坐标间的关系,能运用关于原点成中心对称的点的坐标间的关系进行中心对称图形的变换.
自读,明确当堂目标
自主学习
温故知新
如图,⑴画出点A、B关于x轴的对称点A′
、B′,
点C、D关于y轴的对称点C′、D′
写出点A(-2,1)、B(0,-3)关于x轴的对
称点A′、B′的坐标。点C(-4,-2)、D(5,0)
关于y轴的对称点C′、D′的坐标。
自主完成,
组内交流
设问导学
已知:A(3,2),B(-3,2),C(3,0).在直角坐标系中,画出点A,B,C关于原点的对称点A′,B′,C′;并分别写出对称点的坐标
自主探究
合作探究
归纳:两个点关于原点对称,它们的坐标符号和关于原点的对称点坐标
合作交流
自我检测
见学案
对学
展示交流
小组展示
自我检测自己完成
组长负责组内交流展示
班级展示
巩固训练中题由学生独立分析思考,教师巡回辅导,适时点拨。
组内先交流,然后选两组代表展示
点拨升华
反馈提升
组长组织组员合作学习活动:
组内交流,组长负责反馈
释疑解惑
让学生充分发表意见,提出各自看法。
组内交流解决,师生共析
总结提高
关于原点对称的两点的坐标间的关系
举一反三
拓展提升
略
课堂作业
巩固练习
见学案
先独立完成,再交流
拓展延伸
见学案
板书设计
两个点关于原点对称,它们的坐标符号
,即点P(x,y)关于原点的对称点P′(
,
).
学段
人教版上册
年级
学科
数学
单元
第二十三章
旋转
课题
23.2.1
中心对称
课型
新课
主备学校
主备人
初审人
终审人
合作团队
数学备课组
教学目标
1、通过具体实例认识中心对称,了解中心对称的概念
2、掌握中心对称的性质,理解对应点所连线段被对称中心平分的性质.
教学重点
中心对称的概念和性质.
教学难点
理解中心对称的性质.
导学环节
课堂流程
学法指导
当堂反思
学习目标
通过具体实例认识中心对称,了解中心对称的概念,掌握中心对称的性质,理解对应点所连线段被对称中心平分的性质.
自读,明确当堂目标
自主学习
温故知新
1、什么是轴对称?成轴对称的两个图形有什么性质?2、旋转有哪些性质?
自主完成,
组内交流
设问导学
阅读课本62-64页,思考,讨论合作交流完成下列问题:(1)把图①中一个图案绕点O旋转180°,你有什么发现?(2)如图②,线段AC、BD相交于点O,OA=OC,OB=OD。把△OCD绕点O旋转180°,你有什么发现?
图①
图②
归纳中心对称的定义(略)
自主探究
合作探究
动手:按下列步骤完成⑴画出三角板内部的△ABC;⑵以三角板的一个顶点O为中心,把三角板旋转180°,画出△AˊBˊCˊ;⑶移开三角板;思考:⑴分别连接对称点AA'、BB'、CC'。点O在线段AA'上吗?如果在,在什么位置?⑵△ABC与△A'B'C'有什么关系?归纳:中心对称的性质(略)
合作交流
自我检测
见学案
对学
展示交流
小组展示
自我检测自己完成
组长负责组内交流展示
班级展示
巩固训练中题由学生独立分析思考,教师巡回辅导,适时点拨。
组内先交流,然后选两组代表展示
点拨升华
反馈提升
组长组织组员合作学习活动:
组内交流,组长负责反馈
释疑解惑
让学生充分发表意见,提出各自看法。
组内交流解决,师生共析
总结提高
中心对称的定义及其性质
举一反三
拓展提升
略
课堂作业
巩固练习
1、教材P64
练习1、2.
2、见学案
先独立完成,再交流
拓展延伸
见学案
板书设计
1.中心对称的定义
2.中心对称的性质
(1)
(2)
“大集体”备课导学案基本模板
学段
人教版上册
年级
学科
数学
单元
第二十三章
旋转
课题
23.2.2
中心对称图形
课型
新课
主备学校
主备人
初审人
终审人
合作团队
数学备课组
教学目标
1、正确认识什么是中心对称图形,理解中心对称图形的性质特点.
2、能理解中心对称和中心对称图形的异同.
教学重点
中心对称图形的有关概念及性质。
教学难点
中心对称与中心对称图形的联系与区别.
导学环节
课堂流程
学法指导
当堂反思
学习目标
正确认识什么是中心对称图形,理解中心对称图形的性质特点.掌握中心对称和中心对称图形的异同.
自读,明确当堂目标
自主学习
温故知新
什么叫中心对称、对称中心、关于中心的对称点?关于中心对称的两图形具有什么性质?
自主完成,
组内交流
设问导学
思考,讨论,合作交流完成。归纳得出中心对称图形的定义(略)
自主探究
合作探究
由定义,线段、平行四边形是否市中心对称图形.
合作交流
自我检测
见学案
对学
展示交流
小组展示
自我检测自己完成。
组长负责组内交流展示
班级展示
巩固训练中题由学生独立分析思考,教师巡回辅导,适时点拨。
组内先交流,然后选两组代表展示
点拨升华
反馈提升
组长组织组员合作学习活动:
组内交流,组长负责反馈
释疑解惑
让学生充分发表意见,提出各自看法。
组内交流解决,师生共析
总结提高
注意强调中心对称图形与中心对称的区别与联系.
举一反三
拓展提升
略
课堂作业
巩固练习
下列图形是中心对称图形吗?
如果是中心对称图形,在图中
用点O标出对称中心.
2、如图,在矩形ABCD中,对角线交于点O,过点O的直线交AD与BC于点E、F,AB=2,BC=3,则图中阴影部分的面积是__.
3.课本P66练习1.2.
先独立完成,再交流
拓展延伸
见学案
板书设计
1.中心对称图形的定义2.中心对称图形的性质特点3.中心对称和中心对称图形的异同.
“大集体”备课导学案基本模板
学段
人教版上册
年级
学科
数学
单元
第二十三章
旋转
课题
23.2.3关于原点对称的点的坐标
课型
新课
主备学校
主备人
初审人
终审人
合作团队
数学备课组
教学目标
1、正确认识关于原点对称的两点的坐标间的关系.
2、能运用关于原点成中心对称的点的坐标间的关系进行中心对称图形的变换.
教学重点
关于原点对称点的坐标.
教学难点
探究关于原点对称点的坐标.
导学环节
课堂流程
学法指导
当堂反思
学习目标
认识关于原点对称的两点的坐标间的关系,能运用关于原点成中心对称的点的坐标间的关系进行中心对称图形的变换.
自读,明确当堂目标
自主学习
温故知新
如图,⑴画出点A、B关于x轴的对称点A′
、B′,
点C、D关于y轴的对称点C′、D′
写出点A(-2,1)、B(0,-3)关于x轴的对
称点A′、B′的坐标。点C(-4,-2)、D(5,0)
关于y轴的对称点C′、D′的坐标。
自主完成,
组内交流
设问导学
已知:A(3,2),B(-3,2),C(3,0).在直角坐标系中,画出点A,B,C关于原点的对称点A′,B′,C′;并分别写出对称点的坐标
自主探究
合作探究
归纳:两个点关于原点对称,它们的坐标符号和关于原点的对称点坐标
合作交流
自我检测
见学案
对学
展示交流
小组展示
自我检测自己完成
组长负责组内交流展示
班级展示
巩固训练中题由学生独立分析思考,教师巡回辅导,适时点拨。
组内先交流,然后选两组代表展示
点拨升华
反馈提升
组长组织组员合作学习活动:
组内交流,组长负责反馈
释疑解惑
让学生充分发表意见,提出各自看法。
组内交流解决,师生共析
总结提高
关于原点对称的两点的坐标间的关系
举一反三
拓展提升
略
课堂作业
巩固练习
见学案
先独立完成,再交流
拓展延伸
见学案
板书设计
两个点关于原点对称,它们的坐标符号
,即点P(x,y)关于原点的对称点P′(
,
).
同课章节目录
