人教版九年级下册数学学案:第26章反比例函数复习课(无答案)
文档属性
| 名称 | 人教版九年级下册数学学案:第26章反比例函数复习课(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 163.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 23:21:54 | ||
图片预览

文档简介
导学案序号:
课题:反比例函数
课型:复习课
课时:
学习目标
1.系统复习《反比例函数》并应用;
2.在复习过程中,渗透待定系数法、分类、数形结合等数学思想方法.
复习
重点
反比例函数知识的应用;
复习
难点
反比例函数知识的综合运用
复习
流程
一、反比例函数的解析式
基础知识检测
一般地,形如
______________(
)的函数称为反比例函数.(其中,自变量x的取值范围为___________________________
)
反比例函数解析式还可以表示为_____________和_________________
注:反比例函数需要满足的两个条件:1._________
,2._______________.
考点突破
1.下列函数中哪些是反比例函数?
①
y=3x;
②
y=2x2;
③
xy=-2;
④
y=2x-1;
⑤
;
⑥
.
2.若函数
是反比例函数,则n=______.
变式:若函数
是反比例函数,则n=______.
3.已知y与x成反比例,当x=2时,y=3,则
y与x的关系式为________.
变式训练:已知y与x+2成反比例,当x=1时,y=-3,则
y与x的关系式为_______.
二.反比例函数的图象以及性质
基础知识检测
反比例函数的图象是
.
函数k图象象限x增大,y如何变化
(k≠0)
k>0
______________,y随x的增大而_________.
k<0
______________,y随x的增大而_________.
复习
流程
考点突破
4.若双曲线经过点(-3
,2),则其解析式是______.
5.函数
的图象在第______象限,当x<0时,y随x的增大而______
.
6.函数
的图象在二、四象限内,则m的取值范围是______
.
7.已知点A(x1,y1),B(x2,y2)(x1<0<x2
)都在反比例函数
的图象上,则y1与y2的大小关系(从大到小)为
.
变式训练:已知点A(-2,y1),B(-1,y2),C(4,y3)都在反比例函数
的图象上,则y1
、y2
、y3
的大小关系(从大到小)为
三、反比例函数中的面积问题(数形结合)
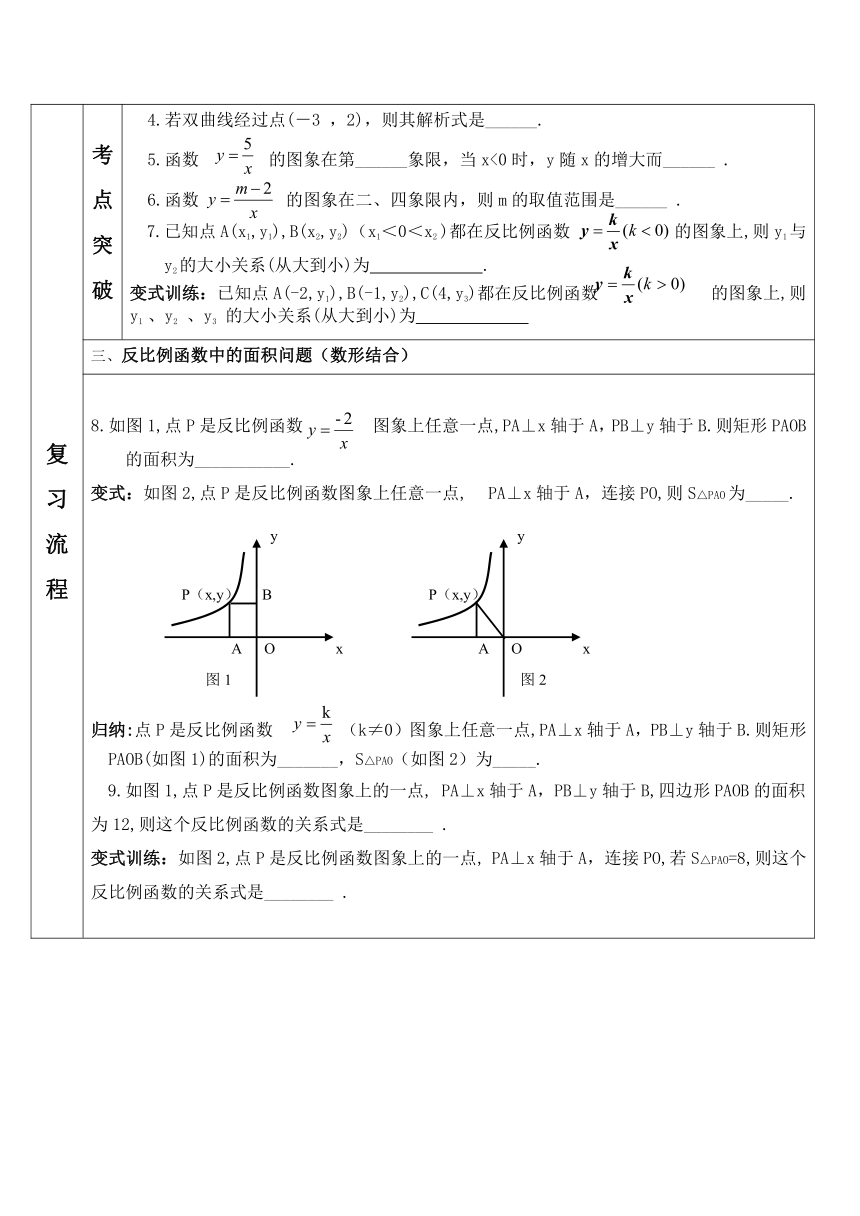
8.如图1,点P是反比例函数
图象上任意一点,PA⊥x轴于A,PB⊥y轴于B.则矩形PAOB的面积为___________.
变式:如图2,点P是反比例函数图象上任意一点,
PA⊥x轴于A,连接PO,则S△PAO为_____.
归纳:点P是反比例函数
(k≠0)图象上任意一点,PA⊥x轴于A,PB⊥y轴于B.则矩形PAOB(如图1)的面积为_______,S△PAO(如图2)为_____.
9.如图1,点P是反比例函数图象上的一点,
PA⊥x轴于A,PB⊥y轴于B,四边形PAOB的面积为12,则这个反比例函数的关系式是________
.
变式训练:如图2,点P是反比例函数图象上的一点,
PA⊥x轴于A,连接PO,若S△PAO=8,则这个反比例函数的关系式是________
.
复
习
流
程
四.反比例函数与一次函数的综合运用
10.如图,一次函数
的图象和反比例函数
的图象交于A、B两点,其中A点坐标为(2,1).
(1)试确定k、m的值;
(2)连接AO,求△AOP的面积;
(3)连接BO,若B的横坐标为-1,求△AOB的面积.
变式训练:
如图:一次函数
的图象与反比例函数
的图象交于M(2,m)、N(-1,-4)两点.
(1)求反比例函数和一次函数的解析式;
(2)当x为何值时,反比例函数的函数值大于一次函数的函数值?
课堂小结
五、知识盘点
1._________________________________;
2._________________________________;
3._________________________________;
4._________________________________.
课堂小结
数学思想方法
1._________________________________;
2._________________________________;
3._________________________________.
拓
展
延
伸
提高题:
如图所示,在直角坐标系中,点是反比例函数
的图象上一点,轴的正半轴于点,是的中点;一次函数的图象经过、两点,并交轴于点若
(1)求反比例函数和一次函数的解析式;
(2)观察图象,请指出在轴的右侧,当时,
的取值范围.
课后反思
课题:反比例函数
课型:复习课
课时:
学习目标
1.系统复习《反比例函数》并应用;
2.在复习过程中,渗透待定系数法、分类、数形结合等数学思想方法.
复习
重点
反比例函数知识的应用;
复习
难点
反比例函数知识的综合运用
复习
流程
一、反比例函数的解析式
基础知识检测
一般地,形如
______________(
)的函数称为反比例函数.(其中,自变量x的取值范围为___________________________
)
反比例函数解析式还可以表示为_____________和_________________
注:反比例函数需要满足的两个条件:1._________
,2._______________.
考点突破
1.下列函数中哪些是反比例函数?
①
y=3x;
②
y=2x2;
③
xy=-2;
④
y=2x-1;
⑤
;
⑥
.
2.若函数
是反比例函数,则n=______.
变式:若函数
是反比例函数,则n=______.
3.已知y与x成反比例,当x=2时,y=3,则
y与x的关系式为________.
变式训练:已知y与x+2成反比例,当x=1时,y=-3,则
y与x的关系式为_______.
二.反比例函数的图象以及性质
基础知识检测
反比例函数的图象是
.
函数k图象象限x增大,y如何变化
(k≠0)
k>0
______________,y随x的增大而_________.
k<0
______________,y随x的增大而_________.
复习
流程
考点突破
4.若双曲线经过点(-3
,2),则其解析式是______.
5.函数
的图象在第______象限,当x<0时,y随x的增大而______
.
6.函数
的图象在二、四象限内,则m的取值范围是______
.
7.已知点A(x1,y1),B(x2,y2)(x1<0<x2
)都在反比例函数
的图象上,则y1与y2的大小关系(从大到小)为
.
变式训练:已知点A(-2,y1),B(-1,y2),C(4,y3)都在反比例函数
的图象上,则y1
、y2
、y3
的大小关系(从大到小)为
三、反比例函数中的面积问题(数形结合)
8.如图1,点P是反比例函数
图象上任意一点,PA⊥x轴于A,PB⊥y轴于B.则矩形PAOB的面积为___________.
变式:如图2,点P是反比例函数图象上任意一点,
PA⊥x轴于A,连接PO,则S△PAO为_____.
归纳:点P是反比例函数
(k≠0)图象上任意一点,PA⊥x轴于A,PB⊥y轴于B.则矩形PAOB(如图1)的面积为_______,S△PAO(如图2)为_____.
9.如图1,点P是反比例函数图象上的一点,
PA⊥x轴于A,PB⊥y轴于B,四边形PAOB的面积为12,则这个反比例函数的关系式是________
.
变式训练:如图2,点P是反比例函数图象上的一点,
PA⊥x轴于A,连接PO,若S△PAO=8,则这个反比例函数的关系式是________
.
复
习
流
程
四.反比例函数与一次函数的综合运用
10.如图,一次函数
的图象和反比例函数
的图象交于A、B两点,其中A点坐标为(2,1).
(1)试确定k、m的值;
(2)连接AO,求△AOP的面积;
(3)连接BO,若B的横坐标为-1,求△AOB的面积.
变式训练:
如图:一次函数
的图象与反比例函数
的图象交于M(2,m)、N(-1,-4)两点.
(1)求反比例函数和一次函数的解析式;
(2)当x为何值时,反比例函数的函数值大于一次函数的函数值?
课堂小结
五、知识盘点
1._________________________________;
2._________________________________;
3._________________________________;
4._________________________________.
课堂小结
数学思想方法
1._________________________________;
2._________________________________;
3._________________________________.
拓
展
延
伸
提高题:
如图所示,在直角坐标系中,点是反比例函数
的图象上一点,轴的正半轴于点,是的中点;一次函数的图象经过、两点,并交轴于点若
(1)求反比例函数和一次函数的解析式;
(2)观察图象,请指出在轴的右侧,当时,
的取值范围.
课后反思
